0 引言
随着科学技术的进步，出现了多种人造动态系统[1]，如军事武器系统、交通运输系统、电力输送系统等.为了分析人造动态系统的复杂行为，一般采用离散事件系统[2-3](discrete event systems，DES)来表述.但复杂系统的很多行为同时涉及宏观状态的确定性和状态演化程度的不确定性，若是仅采用传统的符号逻辑对其分析，难以准确、有效地描述这类系统的动态特征.为了解决该问题，模糊离散事件系统(fuzzy discrete event systems, FDES)[4-5]理论的出现为现实世界中“确定概念下的不确定性问题”以及与不确定性符号推理相关的复杂非线性系统的动态行为提出了一种新的解决方案.虽然上述两种模型均为基于状态的复杂系统行为分析提供了有效方法，但观测条件受限仍是复杂系统在现实情况中存在的一类约束.为了避免状态分析带来的组合爆炸问题，还应尽可能多地考虑可能获取到的其他各类信息对分析过程的支持和对分析结果的修正.
文献[6]使用双模拟等价来处理模糊离散事件系统的分析和控制，以达到更有效地应对模糊性、不精确性和主观性等现实问题；文献[7]研究了一类以观测器为基础的不确定T-S模糊系统的跟踪控制问题，实现了在系统状态不可测及不确定有界情况下对系统状态的跟踪；文献[8]将FDES监督控制引入到机器人导航应用中，提出了一种具有命令融合性的移动机器人行为协调方案，并讨论了基于模糊状态的可控性和可观测度量.
笔者针对复杂系统结构中模糊因果关系与不精确的信息相耦合所产生的状态爆炸问题，提出一种基于在时间维度上的模糊可观程度(observable degree in dimensionality of time，ODDT)的FDES复合因果链层次化解耦方法.
1 基于ODDT的FDES因果链无损解耦方法
1.1 TC-PPN约简算法
为了对复杂系统中携带时间信息的状态进行分析，可运用TC-PPN[9]模型.该模型可在观测条件受限以致事件难以捕获的情况下，根据状态信息所含的时间线索来辨识模糊事件并发现系统隐患.但在TC-PPN中，M0中的某些分量对于网的推理及状态的迁移以及最终的状态标识均没有贡献.因此，笔者提出一种根据抑止弧分析时间区间回溯模型约简的算法(reduction algorithm based on inhibitor arcs, RABIA)，其约简模型如表1所示.
表1 根据抑止弧分析时间区间回溯模型约简的算法
Tab.1 The reduction algorithm based on inhibitor arcs
算法1 ∑'=RABLA∑输入:∑(待约简的TC-PPN)输出:∑'(约简后的TC-PPN)1. for eachi=(s,t)∈I2. ifMσ-0(s)=0∧·s=∅theni→i∅ 将i标记为∅3. elsei→iω4. end if5. end for6. for eachi∅=(s,t)∈I7. s→s∅8. ti→t∅j,tj∈s·\t▷将除t以外s的所有后置变迁标记为∅9. fk→f∅k,fk∈({s}×s·)\I;fl→f∅l,fl∈(s·×S)∩F10. end for11. for eachiω=(s,t)∈I;t→tω12. fm→fωm,fm∈{t}×t·;x→xω,x∈·←t∧x·<213. end for14.del(x),(x∈S∪T∪F)∧(x is(∅∪ω))▷删除∑中所有标记为ω或∅的元素15. while∃t∈T,∀s∈·t:·s=∅∧Mσ-0(s)=0do16. del(f),f=(s,t),s∈t;del(s),s∈t;del(t)17. end while18. ∑'=∑19. return∑'
性质1 设∑TP为一个TC-PPN，其可达状态标识集为R(M0)，则∑TP有且仅有一个状态标识Ml=(Mσ-l,Mυ-l)，满足∀Mυ=(Mσ,Mυ)，Mυ∈
R(M0)：Mσ-l(s)=max{Mσ(s)∧Mυ(s)}⊆Mυ-l(s)，称Ml为∑TP的最终状态.
性质2 设∑TP=(S,T;F,E,I,δ,τ,M0)为一个TC-PPN，∑TP以RABIA算法约简得到∑′，R、R′分别为∑TP和∑′的可达状态标识集，∑TP在∑′的投影为P(R)，则有P(R)=R′.
1.2 解耦模型
基于文献[10]提出的ODDT,构造了FDES的复合因果链解耦算法.该算法由两步构成，笔者将第一步的结果称为Ⅰ型解耦网，第二步的结果称为Ⅱ型解耦网.
令∑TP=(S,T;F,E,I,δ,τ,M0)表示一个由多重因果关系耦合的FDES，TG(∑TP)=(V,Arc,H)为其时间约束图，事件e∈E的时间维度可观程度de定义为：
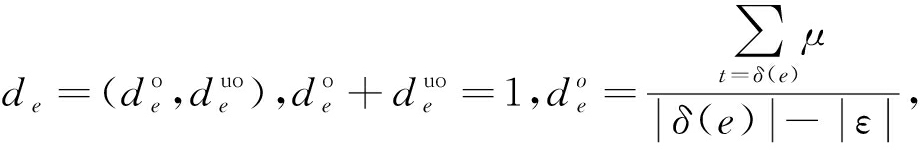
式中：δ为∑TP中模糊时间e到模糊变迁T的子集的映射；ε为位置时间区间；|ε|为t∈δ(e)中μ=ε的数量.μ的计算方法为：
(1)若有si∈·t，sj∈t·:|Vi|>1∨|Vj|>1，则μ=φ(Vi,Vj,τ(t)),
其中，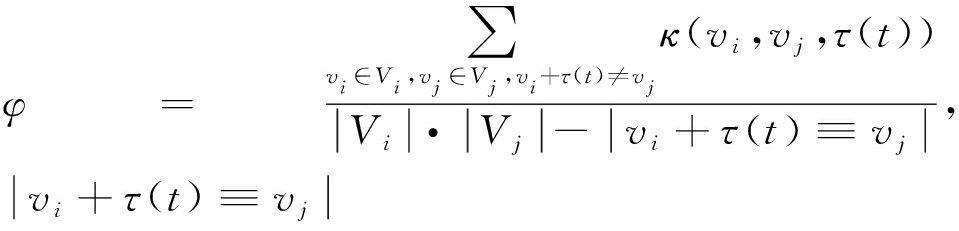
为满足vi+τ(t)=vj的时间区间数量，κ用式(1)计算；φ为非已投票函数.
(2)若si∈·t，sj∈t·:Vi∈V∧Vj∈V，则μ=0.
(3)若si∈·t，sj∈t·:|Vi|=1∧|Vj|=1，则μ=ε，表示状态未知，不参与
的计算.
Ⅰ型解耦网∑Ι为∑TP的一类子网，其构造方法如表2.
性质3 令∑Ⅰ为∑TP的Ⅰ型解耦网，其可达状态标识集为RI，则∑I有且仅有一个状态标识Ml=(Mσ-l,Mυ-l)，满足∀Mυ=(Mσ,Mυ)，Mυ∈RI: (Mσ-l(s)=max{Mσ(s)})∧(Mυ(s)⊆Mυ-l(s))，称Ml为∑I的最终状态.
性质4 令∑I为∑TP的Ⅰ型解耦网，R、RI分别为∑TP和∑I的可达状态标识集，∑TP在∑I的投影为P(R)，则有P(R)=RI.
性质5 令∑I为∑TP的Ⅰ型解耦网，
∑TP=(S,T;F,E,I,δ,τ,M0).
表2 Ⅰ型解耦网构造方法
Tab.2 The construction method of Ⅰ type decoupling network
算法2 ∑I=get Ⅰ Decoupling∑TP输入:∑TP(时间约束可能性Petri网TC-PPN)输出:∑Ι(Ⅰ型解耦网)1. E0=∅;T0=∅;F0=∅;Sin=∅;Snull=∅2. for eachs∈S:s·=∅doSin=Sin∪{s}3. end for4. for eachdTe∈DT:dTe=0doE0=E0∪{e}5. end for6. for each e∈E0doT0=T0∪δ(e)7. end for8. for eacht∈T0doF0=F0∪{(si,t)∈Fsi∈S}∪{(t,sj)∈Fsj∈S}9. end for10. T'=T\T0;F'=F\F0;I'=I\F0;E'=E\E0▷其中x\y表示集合x与y的差集11. ∑temp=(S,T';F',I',E',δ,τ,M0)12. for eachs∈S∧S·in∑temp:s·=∅∧s=∅doSnull=Snull∪{s}13. end for14. S'=S\Snull;∑Ι=(S',T';F',I',E',δ,τ,M0)15. return∑Ι
设
分别为∑TP、∑I的最终状态，SI-in={s|s∈SI∧s·=∅}，Sin={s|s∈S∧s·=∅}，若Sint=Sin∩SΙ-in∧Sint≠∅，则对∀s∈Sint有
令
表3为Ⅱ型解耦网∑Ⅱ的构造方法.
表3为Ⅱ型解耦网构造方法，可证Ⅱ型解耦网具有如下性质.
性质6 令∑Ⅱ为∑TP的Ⅱ型解耦网，其可达状态标识集为RⅡ，则∑Ⅱ有且仅有一个状态标识Ml=(Mσ-l,Mυ-l)，满足∀Mυ=(Mσ,Mυ),Mυ∈RΙ: Mσ-l(s)=max{M(s)}∧Mυ(s)⊆Mυ-l(s)，称Ml为∑Ⅱ的最终状态.
性质7 令∑Ⅱ为∑TP的Ⅱ型解耦网，其中
∑TP=(S,T;F,E,I,δ,τ,M0),
设
分别为∑TP、∑Ⅱ的最终状态，SⅡ-in={s|s∈SⅡ∧s·=∅}，Sin={s|s∈S∧s·=∅}若Sint=Sin∩SⅡ-in且Sint≠∅，则对于∀s∈Sint有
表3 Ⅱ型解耦网构造方法
Tab.3 The construction method of Ⅱ type decoupling network
算法3 ∑Ⅱ=getⅡDecoupling(∑TP,∑Ι)输入:∑TP(时间约束可能性Petri网TC-PPN)∑Ι(Ⅰ型解耦网)输出:∑Ⅱ(Ⅱ型解耦网)1. Sin:=∅2. for eachs∈S:s·=∅doSin:=Sin∪{s}3. end for4. for eachs∈SΙ:s·=∅∧{s}∩Sin=∅∧Mσ-0(s)=0 do5. Ftemp={(t,s)∈F:t∈s}∪{(s,t)∈F:t∈s∧si∈(SΙ\{s})}6. ∑Ι=(SΙ\{s},TΙ\s;FΙ\Ftemp,IΙ,EΙ,δ,τ,M0)end for7. ∑Ⅱ=∑Ι8. return∑Ⅱ
1.3 单纯因果链的解析与隐患搜索
令∑ET=(S,T;F,E,I,δ,τ,M0)为FDES的扩展时间Petri网模型，∑TP=(S′,T′;F′,E′,I′,δ′,τ′,M0)为其求逆得到的TC-PPN.
设Ssr⊆S′:s∈Ssr→Ml(s)>λ∧s·=∅为∑TP最终状态下σ分量大于某个预设值λ的库所集合.表4为根据Ssr进行的单纯因果链的析出算法.
单纯因果链的析出有助于检测FDES的某些隐性状态或事件，这类状态和事件可能受观测条件限制而未被捕获，或者本身即为一类系统隐患，需要进一步对其进行分析.令
为单纯因果链，表5为隐性状态的求取方法.
2 仿真实验
为了验证方法的有效性，以某型武器系统复合因果链的解耦及故障分析过程为例进行仿真实验.
表4 单纯因果链的析出算法
Tab.4 The precipitation algorithm of simple causal chain
算法4 CS=getSimplechain(∑ET,Ssr)输入:∑ET(扩展时间Petri网ETPN)Ssr(已确认的源库所集)输出:CS(析出的单纯因果链的集合,其中每个元素∑SET均为ETPN的子网)1.Ss=∅;Ts=∅;Fs=∅;Es=∅;Is=∅;CS=∅2.for eachs∈SsrdoSs={s}3. whiles∈SS:s·∉TSdo4. TS=TS∪s·;SS=SS∪t·;FS=FS∪{SS×TS}∪{TS×SS}5. ES=ES∪e∈E,δ(e)∈TS;IS=IS∪(S×T)∈I;Ssr=(Ssr∪t·)\s6. end while7. MS=[0,1,…,1]1×SS▷M为1×SS向量,第一个分量为0,其余所有分量均为18. ∑SET=(Ss,Ts;Fs,Is,Es,δ,τ,Ms,);CS=CS∪∑SET9. end for10. returnCS
表5 单纯因果链的隐形状态
Tab.5 The recessive state of simple causal chain
算法5 [Srec,Erec]=get Recessice(∑ET,∑SET)输入:∑ET(扩展时间Petri网ETPN);∑SET(单纯因果链)输出:Srec(隐患状态集);Erec(隐患事件集)1.Srec=∅;Erec=∅2. for eachs∈SSdo3. ifMS(s)=1∧M0(s)=ε∧∀si∈S:M0(si)∈S:M0(si)=0∧(si,·s)∈ Ithen4. Srec=Srec∪{s};Erec=Erec∪e,δ(e)∩(s·∪s)≠∅5. end if6. end for8. returnSrec,Erec
2.1 实验设计
在某型武器系统中，如果某个运行设备发生故障，将会触发相关保护机制的运作.主要的保护装置为继电保护设备和断路器，它们与运行设备相关联.根据文献[11]中统计故障概率，以图1所示的武器系统接线模型进行复合因果链解耦及故障分析，仿真实验根据文献[12]中的数据设计.
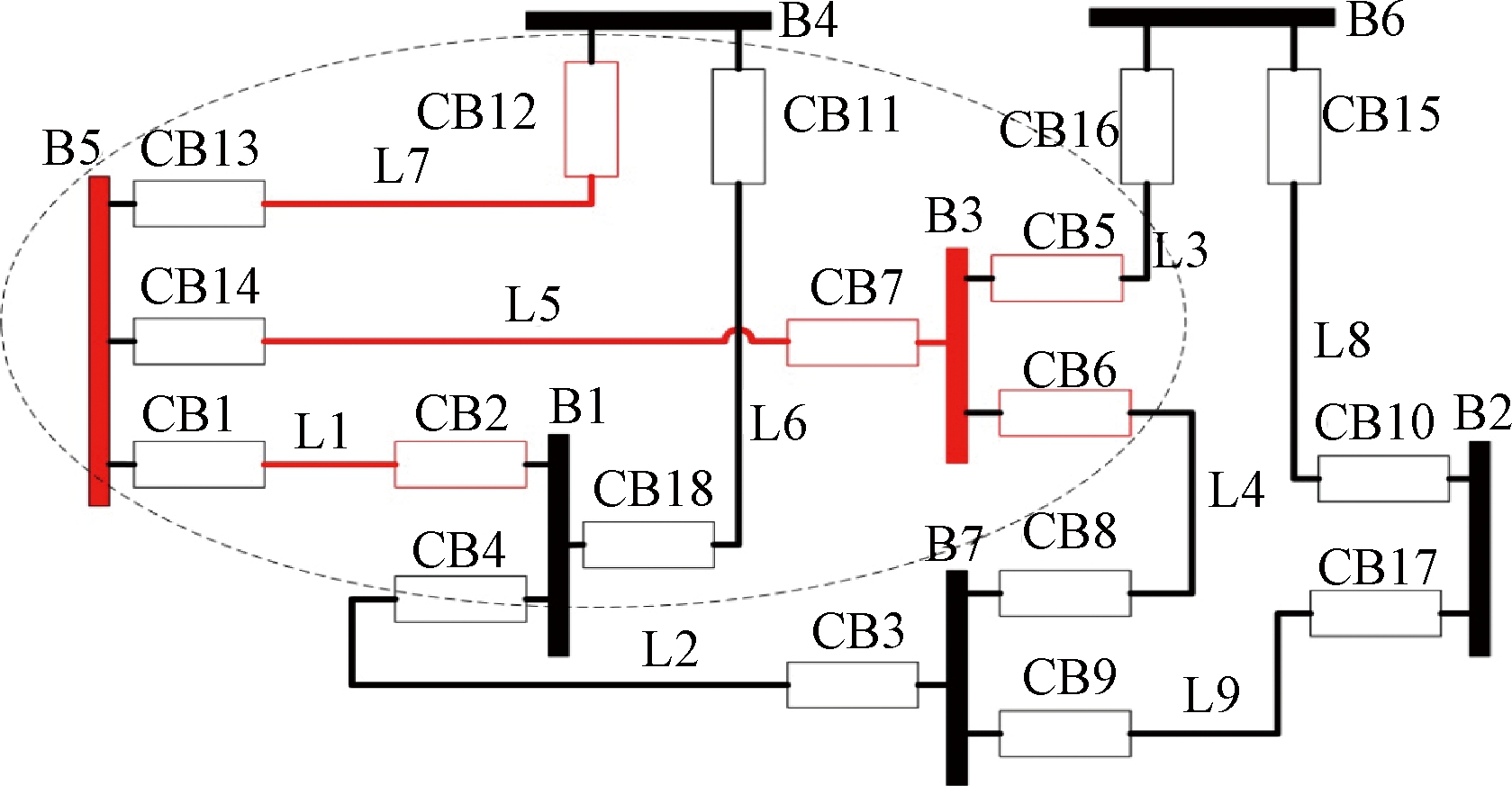
图1 含16个元件的局部某型武器系统模型
Fig.1 A local certain weapon system model with 16 components
(1)数据：设监控系统捕获了如下信息(单位为ms).O(B3m)=45，O(L5Rm)=115，O(L5Sm)=115，O(CB7)=70，O(L1Rs)=615，O(CB5)=72，O(CB6)=80，O(L7Rs)=610，O(CB12)=630，O(CB2)=640.
(2)相关参数：观测数据携带的事件信息符合保护动作及断路器跳闸的时延要求见文献[11].
(3)实验目的：捕获的信息中除了故障引发的正常级联事件外还包含了事件传播过程中存在的各种干扰和信息缺失情况.对其进行分析需要达到两方面目的：一是查找故障源，并计算故障发生的可能性；二是查找差错事件，根据故障蔓延行为分析元件在保护系统中存在的隐患.
2.2 因果链的无损解耦及故障诊断
本实验涉及的系统相对复杂，为了避免对系统整体进行分析而引发状态爆炸问题，采用文献[13]中的方法确定了一个故障搜索范围.另外，考虑到设备故障诊断中的各种不确定性因素，在文献[13]的搜索方法基础上增加对于故障区域边缘元件的诊断.针对观测数据，得到可疑元件集为{B3,B5,L5,L7,L1}，元件所在的位置及观测到的状态以虚线椭圆形在图1中圈出.
根据观测数据及上述规则构造∑ET，并对其求逆，再约简后得到∑′.对∑′中的事件集E={e1,…,e26}及映射函数δ进行列表说明，如表6所示.构造
的时间约束图TG，并根据以TG中推导出的时间约束计算各事件的ODDT，如表7所示.
表6 事件及其变迁集的映射关系
Tab.6 The mapping of events and their transition sets
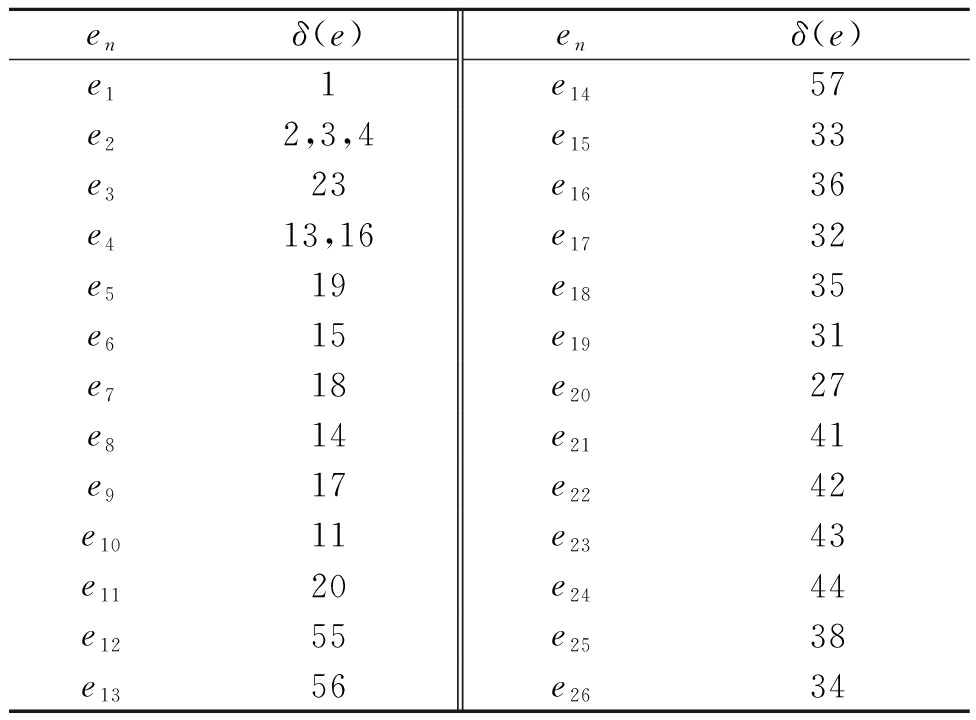
enδ(e)enδ(e)e11e1457e22,3,4e1533e323e1636e413,16e1732e519e1835e615e1931e718e2027e814e2141e917e2242e1011e2343e1120e2444e1255e2538e1356e2634
根据事件的ODDT由算法4构造∑′的 Ⅰ 型解耦网∑Ⅰ如图2所示，字母含义详见文献[11].在∑Ⅰ基础上根据算法5构造Ⅱ型解耦网∑Ⅱ，并进行整理以便明晰因果关系如图3，字母含义详见文献[11].
比较图1及图3可知，经一次化简和两次解耦后，模型结构的复杂度已大大降低，库所的数量从42个减少到13个，变迁从56个减少到13个，弧的数量从117条减到26条.若以模型结构压缩的观点看，通过以上方法处理后的
各元素的压缩比率分别为：库所69%，变迁77%，弧78%.
表7 事件及其ODDT值
Tab.7 Events and their ODDT values
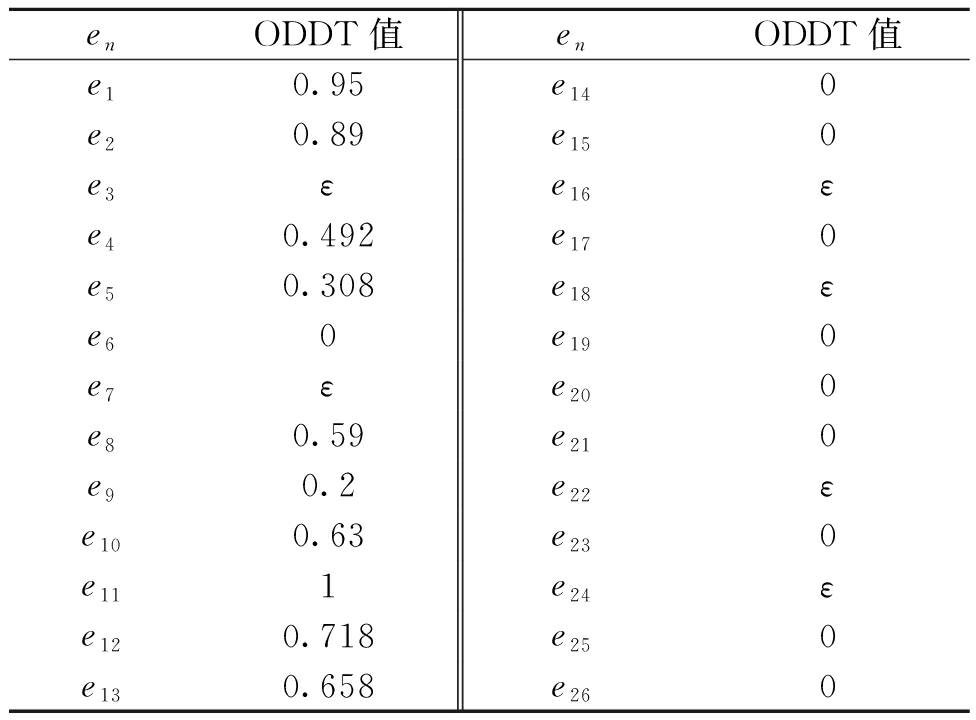
enODDT值enODDT值e10.95e140e20.89e150e3εe16εe40.492e170e50.308e18εe60e190e7εe200e80.59e210e90.2e22εe100.63e230e111e24εe120.718e250e130.658e260
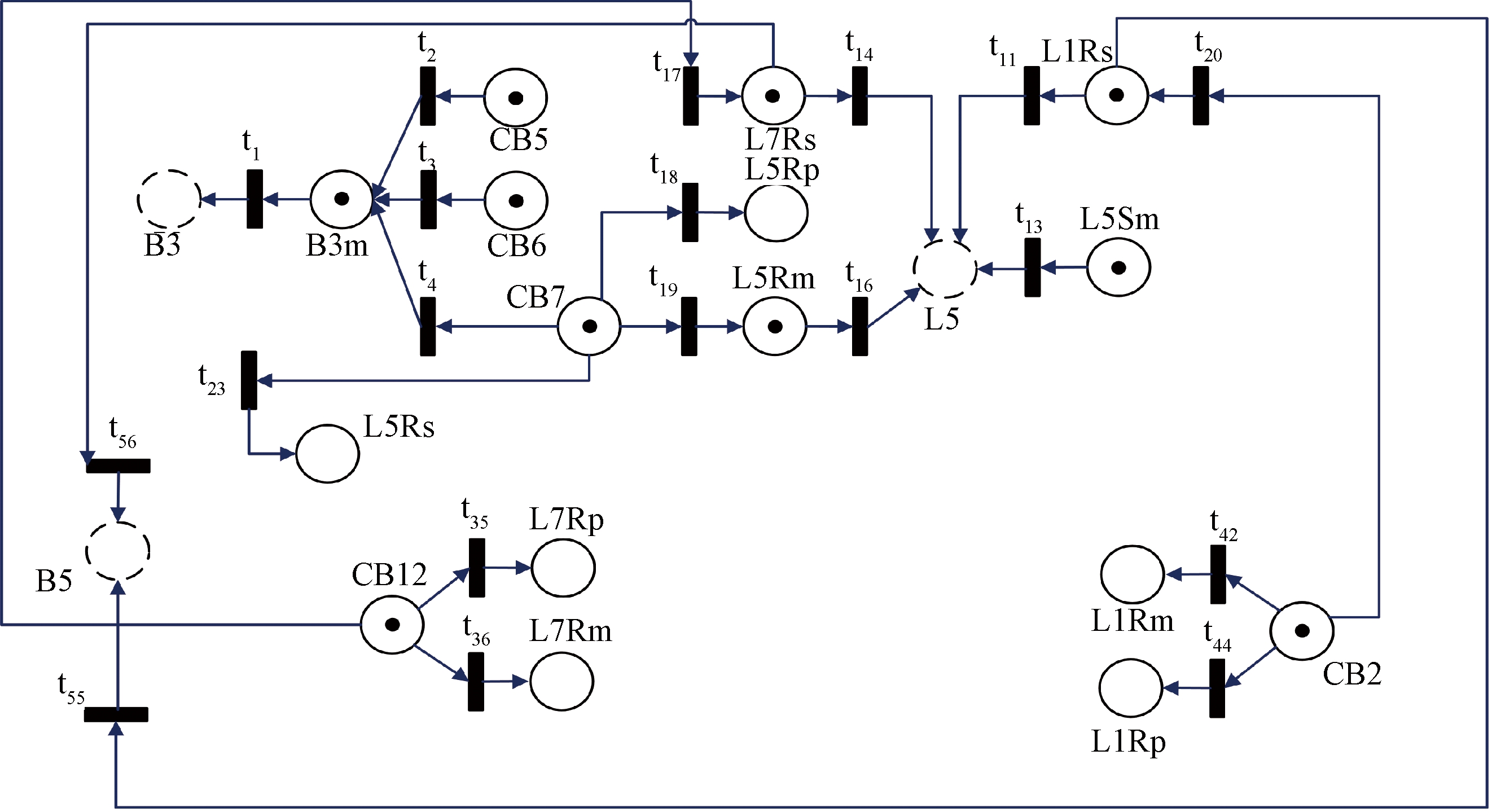
图2 Ⅰ型解耦网
Fig.2 Ⅰ type decoupling network
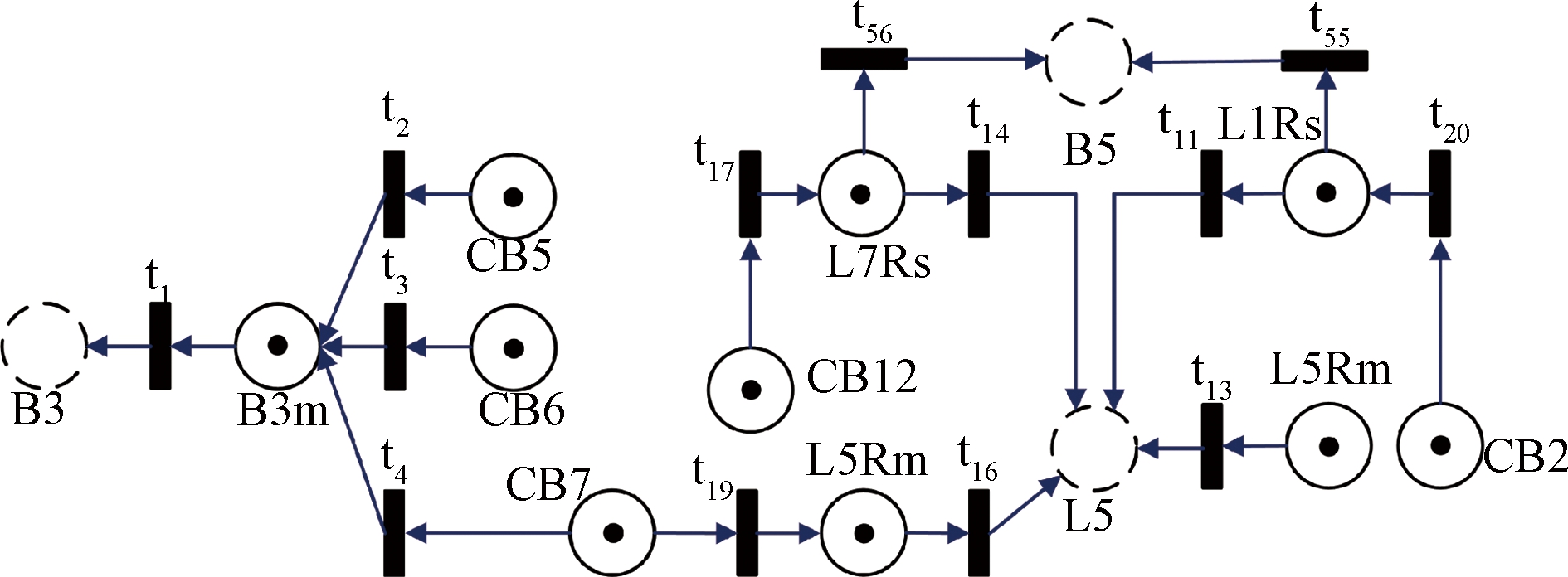
图3 Ⅱ型解耦网
Fig.3 Type Ⅱ decoupling network
将
中各元素整理如下：
(1)SⅡ={B3,B3m,CB5,CB6,CB7,L5,L5Sm,L5Rm,L1Rs,L7Rs,CB2,CB12,B5}.
(2)TⅡ={t1,t2,t4,t11,t13,t14,t16,t17,t19,t20,t55,t56}，FⅡ如图所示；IⅡ={}.
(3)EⅡ={e1,e2,e4,e5,e8,e9,e10,e11,e12,e13}.
(4)解耦后事件及变迁集的映射关系如表8所示.
表8 解耦后的事件及其变迁集的映射关系
Tab.8 The mapping relationship between decoupled events and their transition sets
eδ(e)eδ(e)e11e1457e22,3,4e1533e413,16e1732e519e1835e814e2141e917e2242e1011e2343e1120e2444e1255e2538e1356e2634
(5)τ(t1)=τ(t16)=τ(t13)=[-40,-10],τ(t2)=τ(t3)=τ(t4)=τ(t17)=τ(t19)=τ(t20)=[-40,-20],τ(t11)=τ(t14)=τ(t55)=τ(t56)=[-540,-510].
(6)Mσ-0=[0,1,1,1,1,0,1,1,1,1,1,1,0]；Mv-0={ε,[45,45],[72,72],[80,80],[70,70],ε,[120,120],[115,115],[615,615],[610,610],[640,640],[630,630],ε}.
(7)计算各变迁的p(t·|·t)；将其转化为相应的可能性π(t·|·t)，即事件触发矩阵的各元素.
如表9.此时各事件均满足触发条件，令某一触发序列为e2e1e5e9e11e4e8e10e12e13，可得：
由此可知，在∑TP中L5发生故障的可能性最高，为0.993 1，故障可能发生的时间应在[60,110]；B3发生故障的可能性为0.908 5，可能发生于[0,40]；B5发生故障的可能性为0.072 8，可能发生于[60,110].由于B5发生故障的可能性过于小，因此，认为L5与B3发生了故障.
表9 事件触发矩阵元素值
Tab.9 Event triggered matrix element values
tπ(t·|·t)tπ(t·|·t)t10.908 5t160.993 1t20.489 1t171t30.489 1t191t40.489 1t201t110.993 1t550.707 28t130.993 1t560.707 28t140.993 1
2.3 实验对比
以文献[14]中的局部电力系统为例进行对比实验，诊断结果如表10所示.
表10 诊断效果比较
Tab.5 Comparison of diagnosis effect
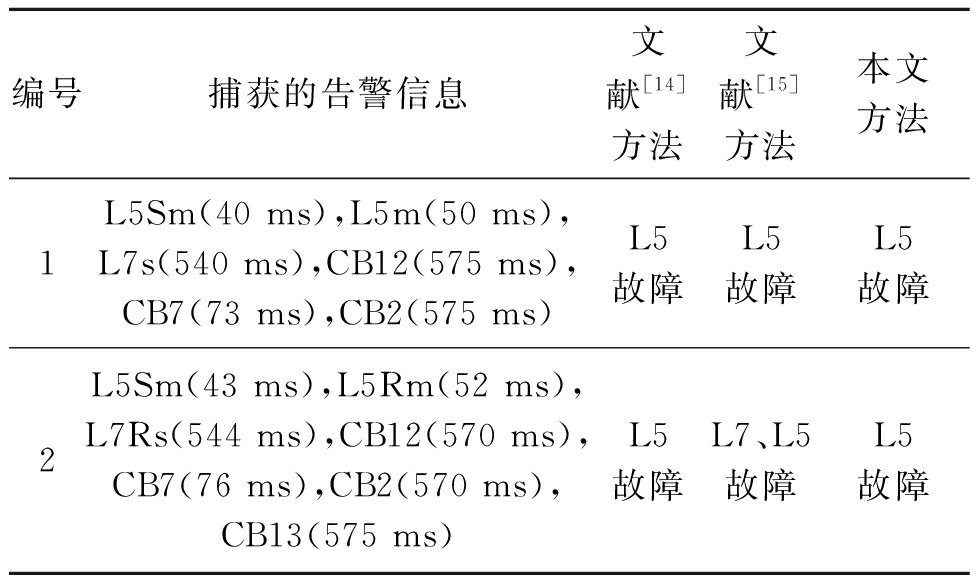
编号捕获的告警信息文献[14]方法文献[15]方法本文方法1L5Sm(40 ms),L5m(50 ms),L7s(540 ms),CB12(575 ms),CB7(73 ms),CB2(575 ms) L5故障 L5故障 L5故障 2L5Sm(43 ms),L5Rm(52 ms),L7Rs(544 ms),CB12(570 ms),CB7(76 ms),CB2(570 ms),CB13(575 ms) L5故障L7、L5故障L5故障
分析两组结果可知:
①第1组告警信号为时序无差错的告警信息，文献[13-14]所述方法与本文方法均能得到准确一致的诊断结果.②在第2组告警信息中CB12(570 ms)、CB13(575 ms)的同时出现使得基于时序分析的时间溯因方法判断L7、L5故障；而贝叶斯网络方法及本文方法在计算了事件发生的概率后，过滤掉了L7故障的误报.
3 结论
笔者针对复杂系统结构中模糊因果关系与不精确的信息相耦合所产生的状态爆炸问题，提出一种基于ODDT的FDES复合因果链层次化解耦方法.该方法充分利用了观测数据中的时间线索及其蕴含的概率信息，可从根本上层次化地解耦模型中的复杂关系，将模糊的因果关系清晰化，降低问题的求解难度，并以较小的代价进行系统状态求取和行为分析，较之单一使用因果联系或条件概率进行解耦的方法更为可靠.
[1] LEI M. On controlling prioritized discrete event systems with real-time constraints[J]. Discrete event dynamic systems, 2018,28(3): 427-447.
[2] SASI Y, LIN F. Detectability of networked discrete event systems[J]. Discrete event dynamic systems, 2018,28(3): 449-470.
[3] 文习明,余泉,常亮,等. 不确定观测下离散事件系统的可诊断性[J]. 软件学报, 2017, 28(5): 1091-1106.
[4] 刘清兰, 王飞, 张波业,等. 模糊离散事件系统的多故障诊断[J]. 华侨大学学报(自然科学版), 2018,39(1): 115-120.
[5] 佘维,叶阳东,陈倩. 基于EFPN的模糊离散事件系统可诊断性分析[J]. 计算机科学, 2014, 41(7): 62-67.
[6] XING H Y, ZHANG Q S, HUANG K S. Analysis and control of fuzzy discrete event systems using bisimulation equivalence[J]. Theoretical computer science, 2012, 456: 100-111.
[7] 张恒艳, 高中文, 李文龙,等.不确定T-S模糊系统的跟踪控制器设计[J]. 郑州大学学报(工学版), 2016, 37(2): 15-19.
[8] JAYASIRI A, MANN G K I, GOSINE R G. Behavior coordination of mobile robotics using supervisory control of fuzzy discrete event systems[J]. IEEE transactions on systems， man & cybernetics，part B,2011, 41(5): 1224-1238.
[9] 路光辉,佘维,雍明超,等. 一种基于时间约束可能性Petri网的设备状态分析模型[J]. 计算机应用研究, 2017, 34(11): 3262-3266.
[10] 佘维, 杨慕, 陈倩,等. 模糊离散事件系统时间维度可诊断性分析[J]. 合肥工业大学学报(自然科学版), 2015, 38(7): 906-913.
[11] 周玉兰,王玉玲,赵曼勇. 2004年全国电网继电保护与安全自动装置运行情况[J]. 电网技术, 2005, 29(16): 42-48.
[12] 杨健维,何正友,臧天磊. 基于方向性加权模糊 Petri 网的电网故障诊断方法[J]. 中国电机工程学报, 2010, 30(34): 42-49.
[13] 吴欣,郭创新,曹一家. 基于贝叶斯网络及信息时序属性的电力系统故障诊断方法[J]. 中国电机工程学报, 2005, 25(13): 14-18．
[14] 马贺贺,胡益,侍洪波. 基于马氏距离局部离群因子方法的复杂化工过程故障检测[J]. 化工学报, 2013, 64(5): 1674-1682.