0 引言
随着计算机技术的飞速发展，数值分析与仿真技术已经被广泛应用于工业设计和生产过程中，例如静力学分析[1]、热力学分析[2]、裂纹扩展分析[3]等，数值计算方法是有效的分析手段之一.边界元法[4]利用微分方程的解析基本解作为边界积分方程的核函数，是一种半解析的数值计算方法，通常精度较高，特别是对于求解裂纹等奇异性问题[5]有天然优势.但奇异积分则是边界元法求解物理问题时的难点，当积分场点和源点位于同一个单元内时，两者距离可能为零，由于距离因子r位于核函数的分母上，因此r趋向于大于0时将导致核函数值无穷大，得到错误的结果，因此需要采取措施避免场点和源点的重合.在传统的单元细分法中，根据奇异单元的形状以及源点在单元中的位置，将源点与单元中各节点相连接，原单元被细分为若干个三角形子单元，从而能够避免源点和场点的重合[6].Zhang等[7-8]曾将该方法与一种新的坐标变换法相结合消除了三维势问题的奇异性，后来又提出了一种自适应单元细分法[9]来提高积分精度.周焕林等[10]提出了一种解析积分算法和单元细分相结合的方法解决了二维各向异性位势问题中的近奇异积分.
上述细分法应用于静态问题时计算精度较高. 对于动态问题，例如笔者所关注的弹性动力学问题[11-12]基本解更加复杂，不仅包含空间变量，还包含时间变量，且为分段函数(表现为纵波和横波两个波动前沿).如果仍然采用传统的单元细分法，则无法将波动前沿对核函数的影响考虑进去，奇异积分的精度必然会受到影响，因此笔者根据三维问题中弹性波传播的规律以及核函数的分段特性，将波速和时间步长考虑在内，提出了一种新的单元细分法.结合文献[8]中的坐标变换有效地消除了基本解中的奇异性，提高了积分的精度，最后通过两个算例验证该方法的准确性和计算精度.
1 弹性动力学问题的时域边界积分方程
对于均匀、各向同性的线弹性材料而言，弹性动力学问题的位移运动方程(亦称为控制方程)如下[12]：
(1)
式中：q代表弹性体上的任意一点；i、j=1、2、3；ui代表位移分量；
是位移对时间的二次导数，也就是加速度；bi代表单位质量的体积力；ρ是材料密度；λ和G是拉梅常数，表达式如下：
(2)
式中：E表示弹性模量；ν表示泊松比.
由于笔者研究的重点为奇异积分处理中的单元细分方法，而奇异积分主要出现在边界积分中，因此为了叙述方便，设问题的初始条件和体积力均为零(不为零时关于奇异积分的处理仍然是一样的)，此时控制方程(1)对应的时域边界积分方程为[12]：
(3)
式中：S表示弹性体的边界；
是位移基本解，表示t时刻场点q在j方向上的位移分量
该位移分量是由τ时刻源点p在i方向上的单位集中引起的；
是面力基本解，位移和面力基本解的具体表达式可参考文献[12]；当源点p位于光滑边界时,Cij(p)=δij/2，位于域内时,Cij(p)=δij.
2 边界积分方程中奇异积分的处理
方程(3)中的基本解经过时间离散和积分后称为核函数，根据该问题位移核函数的表达式作出能表示其变化趋势的示意图,如图1所示.图1中在r=c1Δt和r=c2Δt处均发生了函数值的突变(图1中：横坐标r代表场点距离源点的距离；纵坐标Uij代表位移核函数值；c1代表纵波的波速；c2代表横波的波速；Δt代表时间步长)，即在波动前沿处核函数值会产生突变.当源点位于积分单元内且c1Δt<d(d代表单元尺寸)时，作波动前沿的示意图，如图2所示，图中由源点p产生的两处波动前沿(虚线圆所示)将积分单元(四边形所示)划分为1、2、3三个区域，这3个区域的核函数值不连续，特别是在1号区域的函数值全部为零，因为波动还未传播到该区域.如果直接按照传统的细分法进行奇异单元的细分，则无法将这3个区域的不同考虑进去，必然将导致计算精度的降低.
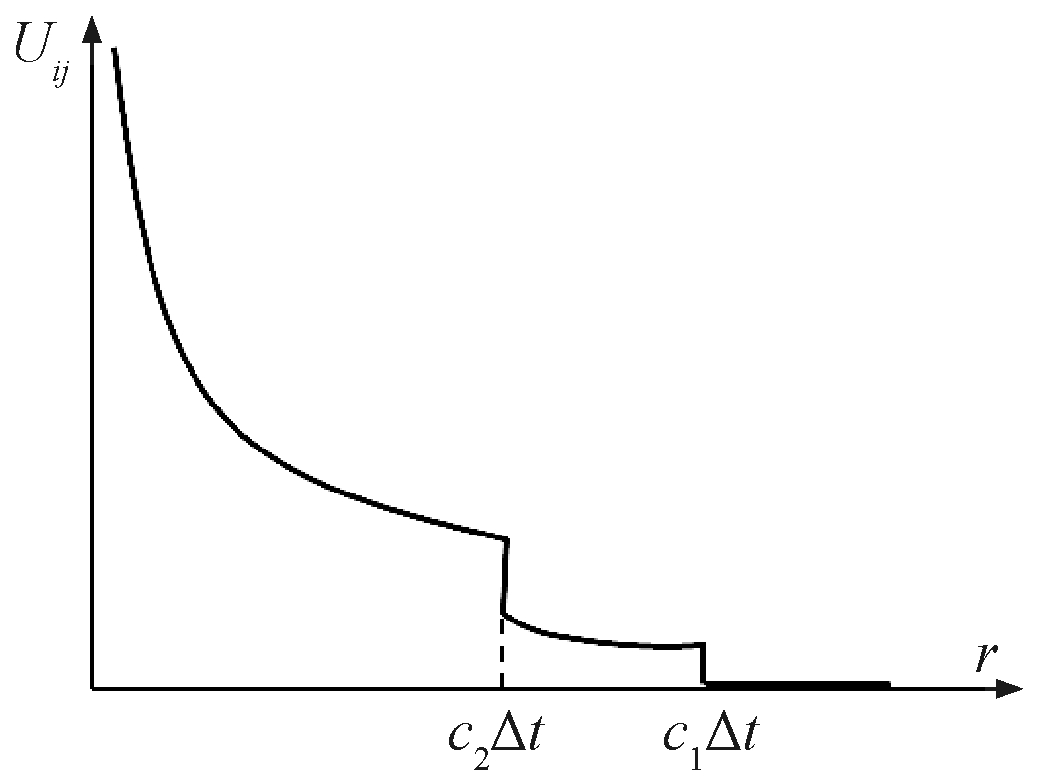
图1 位移核函数曲线示意图
Fig.1 Diagram of the displacement kernel function curve
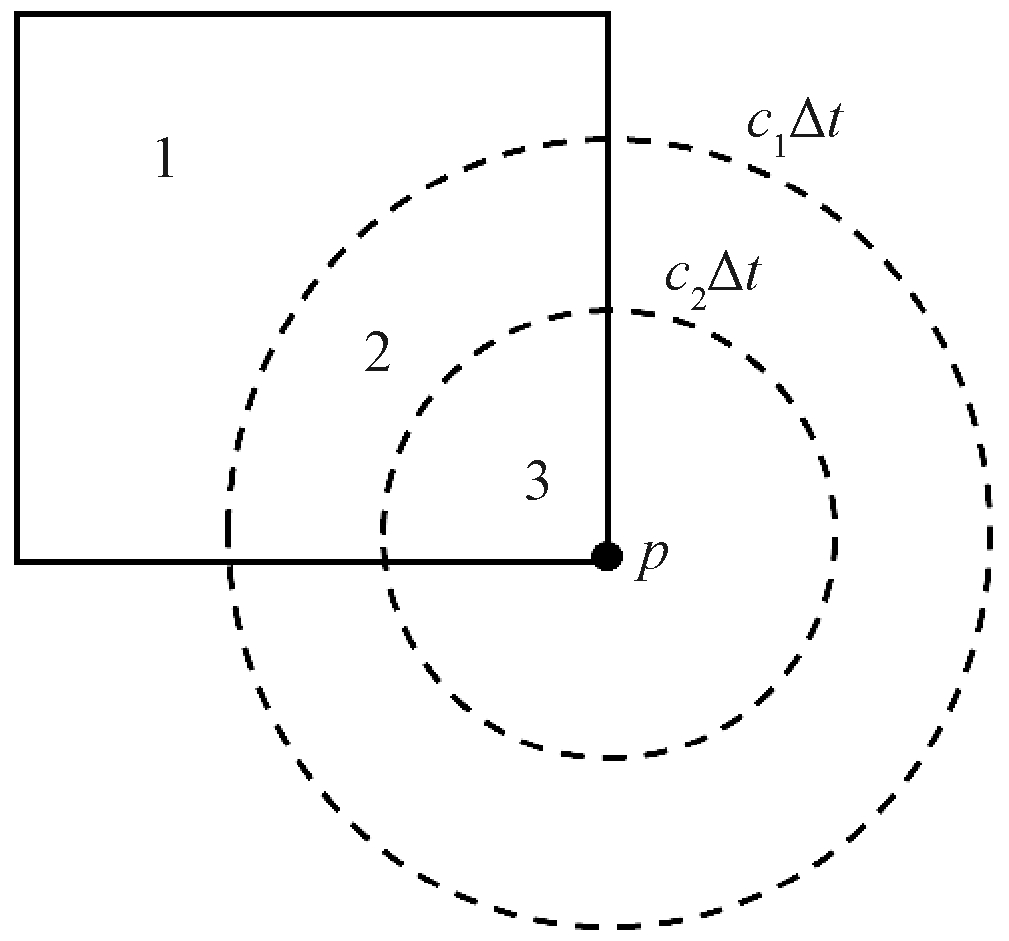
图2 波动前沿示意图
Fig.2 Diagram of the wave front edge
基于以上考虑，根据单元尺寸和时间步长之间的关系，笔者将奇异积分的单元分3种情况进行细分.
(1)当c2Δt≥d时，细分方法如图3所示，传统单元细分法采用的就是这种方式，而在本方法中该细分方式只是其中之一.当源点位于单元的角点上时，将源点与对角点相连，如图3(a)所示，原单元被细分为两个三角形子单元；当源点位于单元的边上时，如图3(b)所示，将源点与其他两个节点分别相连形成3个三角形子单元；当源点位于单元内时，如图3(c)所示，将源点与4个节点分别相连形成4个三角形子单元.在细分后的子单元内积分时，不会再出现场点与源点重合的情况.第1种细分法出现的概率很小，因为时间步长过大时计算结果的振幅衰减过快，精度很低.
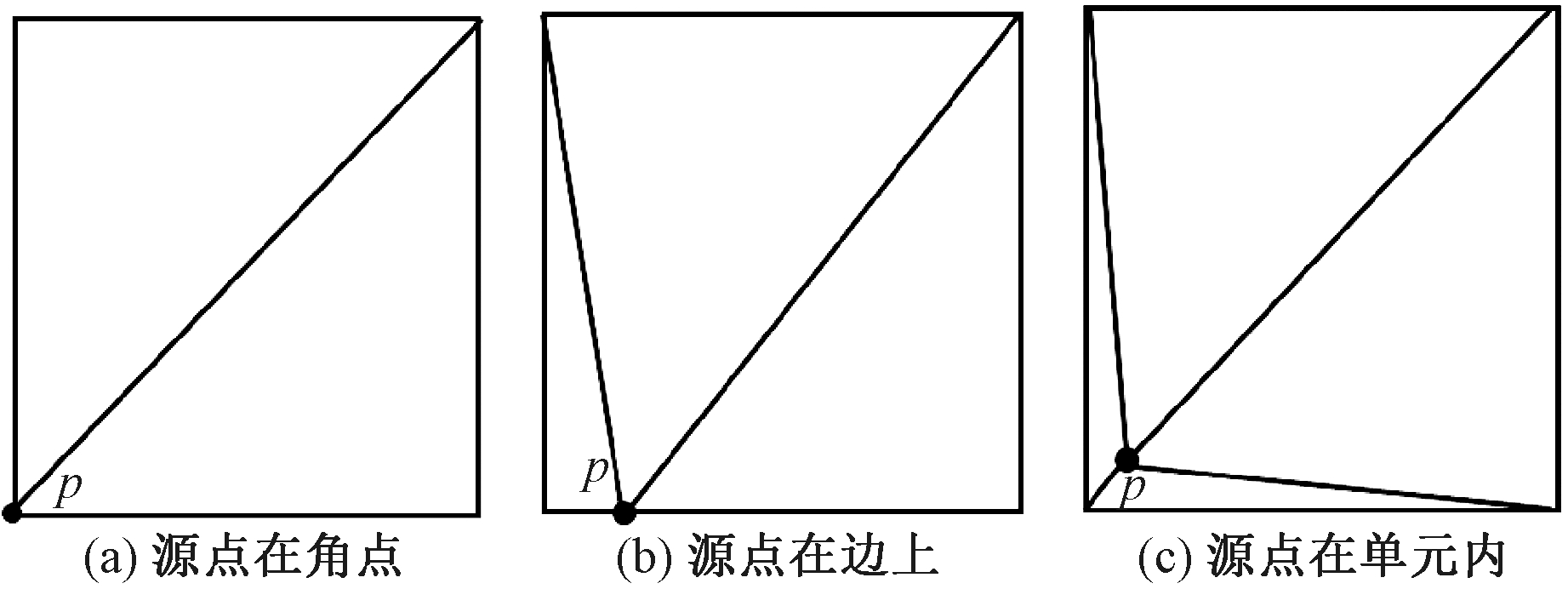
图3 第1种单元细分方式
Fig.3 The first kind of element subdivision method
(2)当c2Δt<d<c1Δt时，细分方法如图4所示.此时纵波波动前沿位于单元外面，横波波动前沿与单元相交(图中圆弧形点画线所示).无论源点位于单元的角点、边上或单元内，均依据以下步骤进行单元细分：①求出波动前沿与单元边界的交点，根据交点位置划分出一个包含源点的四边形块(左下角的实线四边形所示)；②将源点p分别与四边形块的各个角点相连接，得到连线与波动前沿的交点，将该交点再与四边形块的其他角点相连；③根据左下角的四边形块将积分单元的其他部分划分为3个四边形块.最终得到的分块结果如图4中实线所示，原单元被分为若干个三角形和四边形块，此时只在包含源点的三角形块中采用奇异积分即可，其他分块区域只需采用近奇异积分或正则积分.
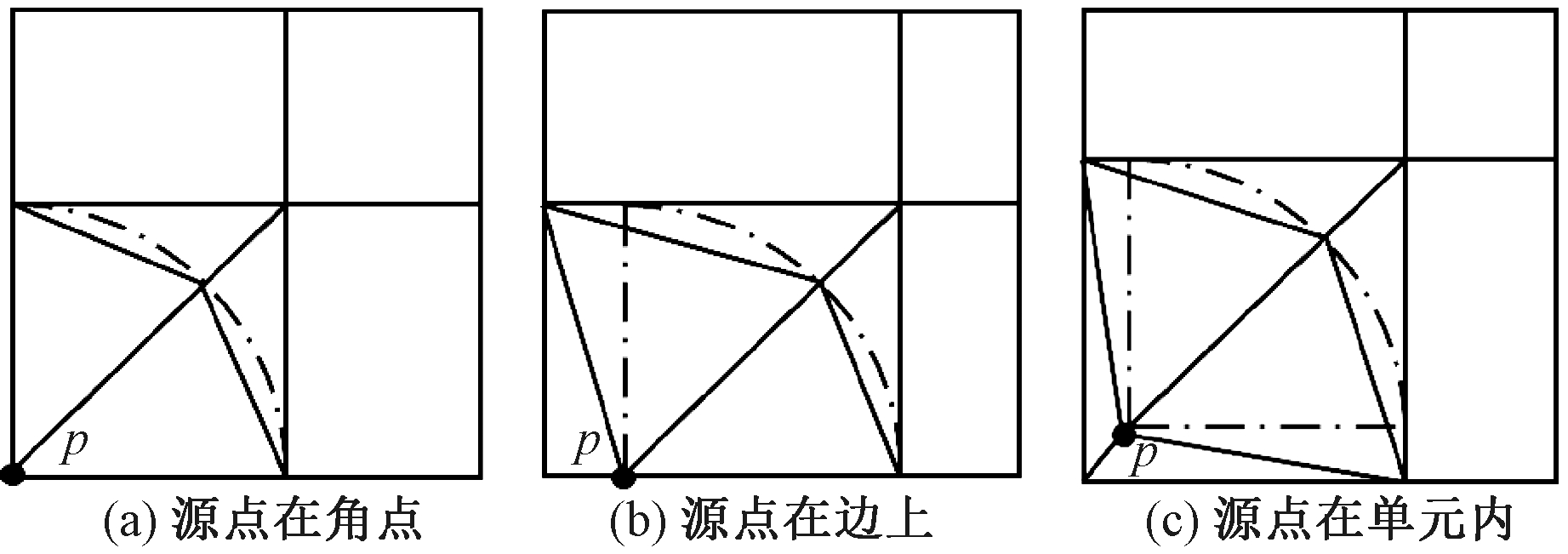
图4 第2种单元细分方式
Fig.4 The second kind of element subdivision method
(3)当d≥c1Δt时，细分方法如图5所示.此时横波和纵波的波动前沿都与单元相交，如图中圆弧形点画线所示.首先按照第二种情况的步骤处理包含横波波动前沿的四边形块；然后求出纵波波动前沿与单元边界的交点，根据交点位置将单元的其他部分划分为若干个四边形块，最终得到的分块结果如图5中的实线所示.同样的，只在包含源点的三角形块中采用奇异积分即可，其他分块区域只需采用近奇异积分或正则积分.
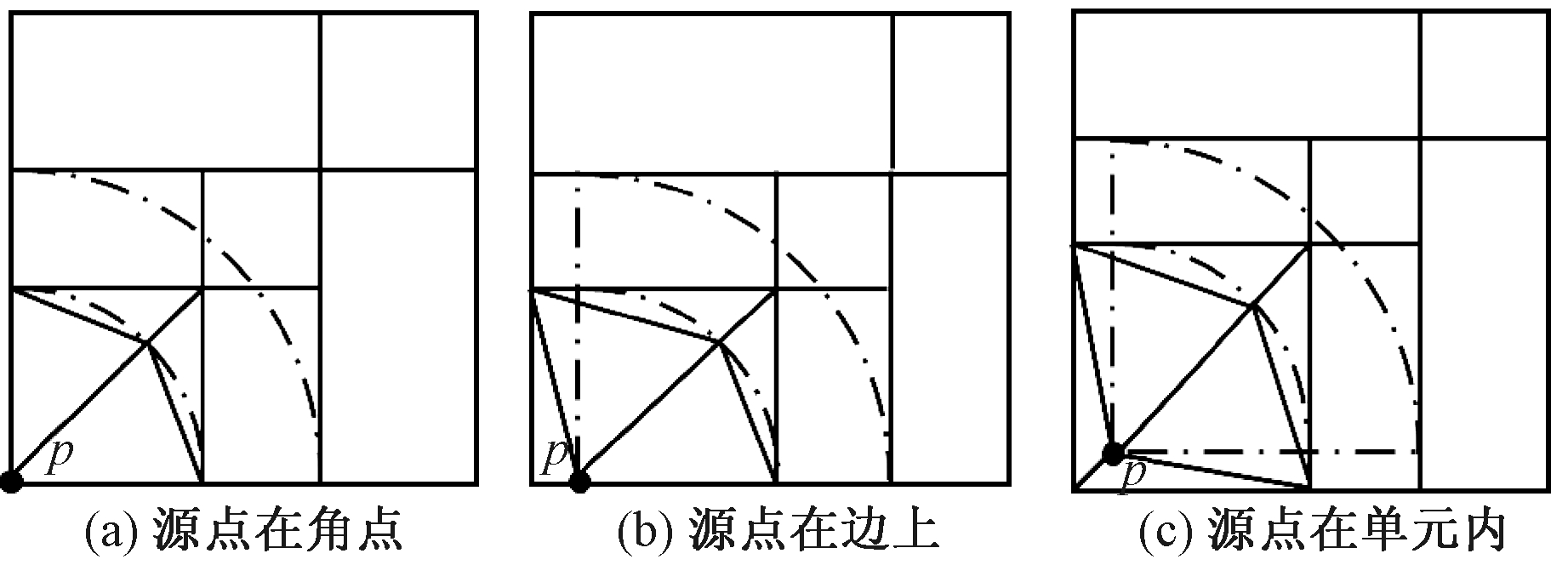
图5 第3种单元细分方式
Fig.5 The third kind of element subdivision method
与传统的单元细分法相比，这种改进的方法能够根据波动前沿的位置动态改变单元细分方式，在被波动前沿波及的区域布置更多的积分点，得到更高的奇异积分精度，而在波动前沿还未到达的区域无需布置积分点.需要注意的是，奇异积分只发生在第一个分析步，后面的分析步无需使用单元细分法.下面将通过两个数值算例对比改进后和改进前计算结果的精度.
3 数值算例
3.1 悬臂梁在Heaviside类型载荷下的动态响应
本例以悬臂梁为分析模型，模型的几何尺寸如图6所示.边界条件：左端面约束所有方向的自由度，右端面施加值为1 000 Pa的均布载荷，载荷为沿x轴正方向的Heaviside类型的均布力.材料参数：弹性模量E=1.1×105 Pa，密度ρ=2.0 kg/m3，泊松比ν=0.当泊松比为0时，该问题可通过理论方法计算出解析解.因此本例中将泊松比设置为0，是为了得到数值解的计算误差，在程序中仍然将该问题当作三维问题来计算.根据文献[13]可得到悬臂梁上任意一点任意时刻的位移响应计算公式：
(4)
式中：
是一维问题中弹性波的波速.
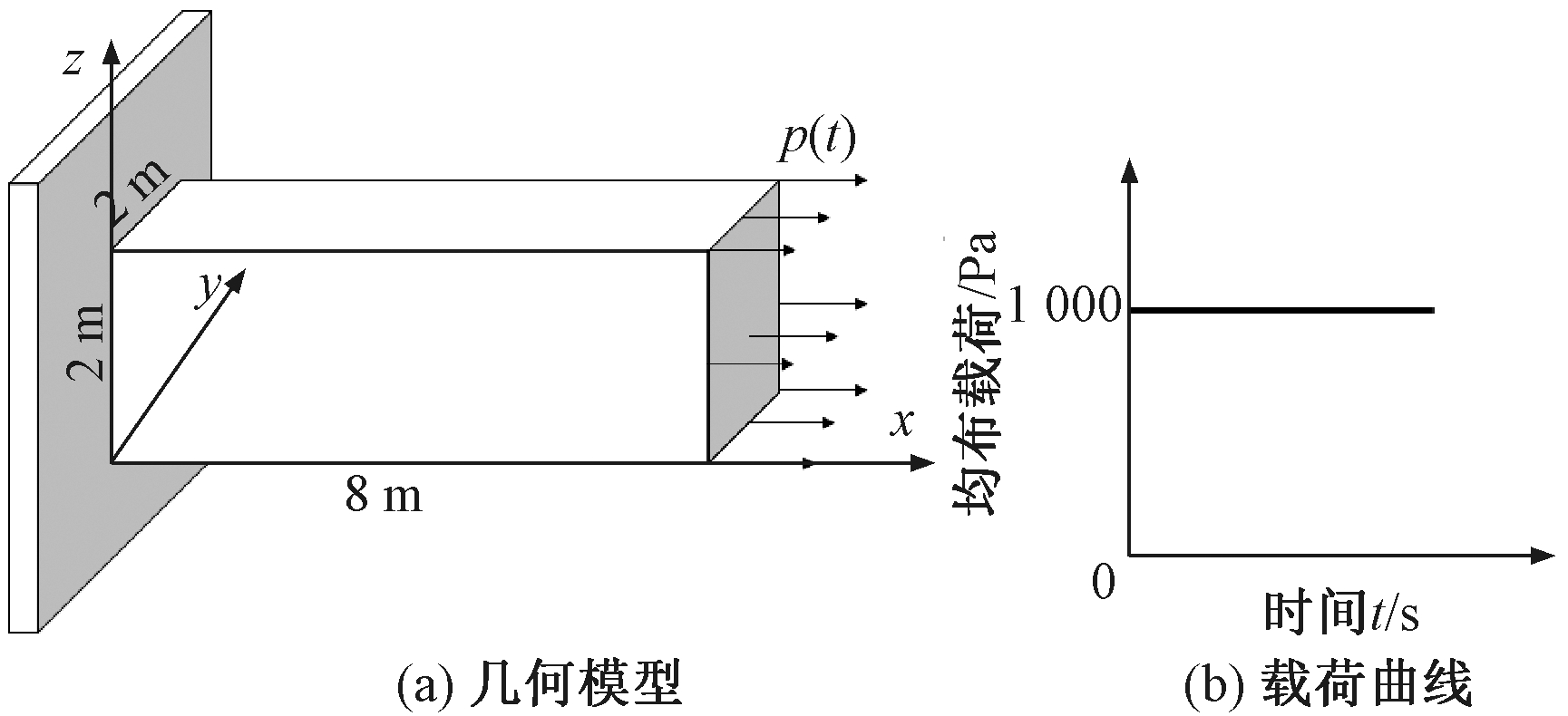
图6 悬臂梁模型和载荷曲线示意图
Fig.6 Diagram of the model and load curve of the cantilever beam
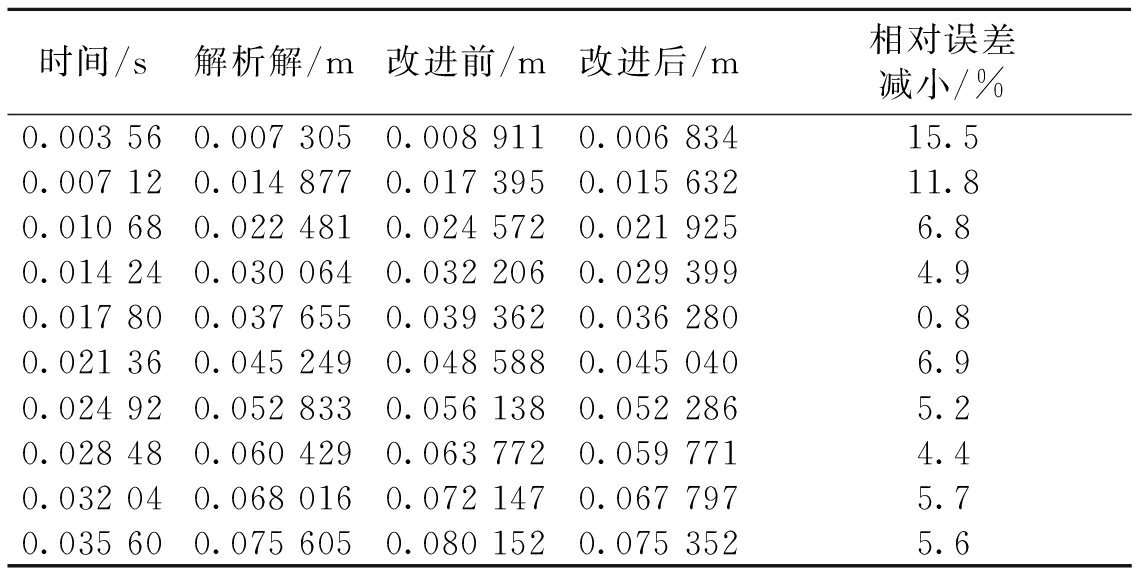
采用尺寸为1 m的线性四边形单元离散模型.首先取时间步长Δt=0.003 56 s，得到前10个分析步的计算结果.表1给出了悬臂梁自由端位移的响应，表中最后一列的数值等于改进前结果的相对误差减去改进后结果的相对误差，可以看出改进后相对误差明显减小，尤其是存在奇异积分的第一个分析步结果的相对误差减小了15.5%.将结果绘制成曲线，如图7所示.图7中exact曲线代表精确解，traditional曲线代表改进前的结果，improved曲线代表改进后的结果.可以明显看出改进后的结果与精确解更加吻合.
表1 Δt=0.003 56 s时悬臂梁自由端位移随时间的变化
Tab.1 The displacement of the free end of the cantilever beam with time when Δt=0.003 56 s
时间/s解析解/m改进前/m改进后/m相对误差减小/%0.003 560.007 3050.008 9110.006 83415.50.007 120.014 8770.017 3950.015 63211.80.010 680.022 4810.024 5720.021 9256.80.014 240.030 0640.032 2060.029 3994.90.017 800.037 6550.039 3620.036 2800.80.021 360.045 2490.048 5880.045 0406.90.024 920.052 8330.056 1380.052 2865.20.028 480.060 4290.063 7720.059 7714.40.032 040.068 0160.072 1470.067 7975.70.035 600.075 6050.080 1520.075 3525.6
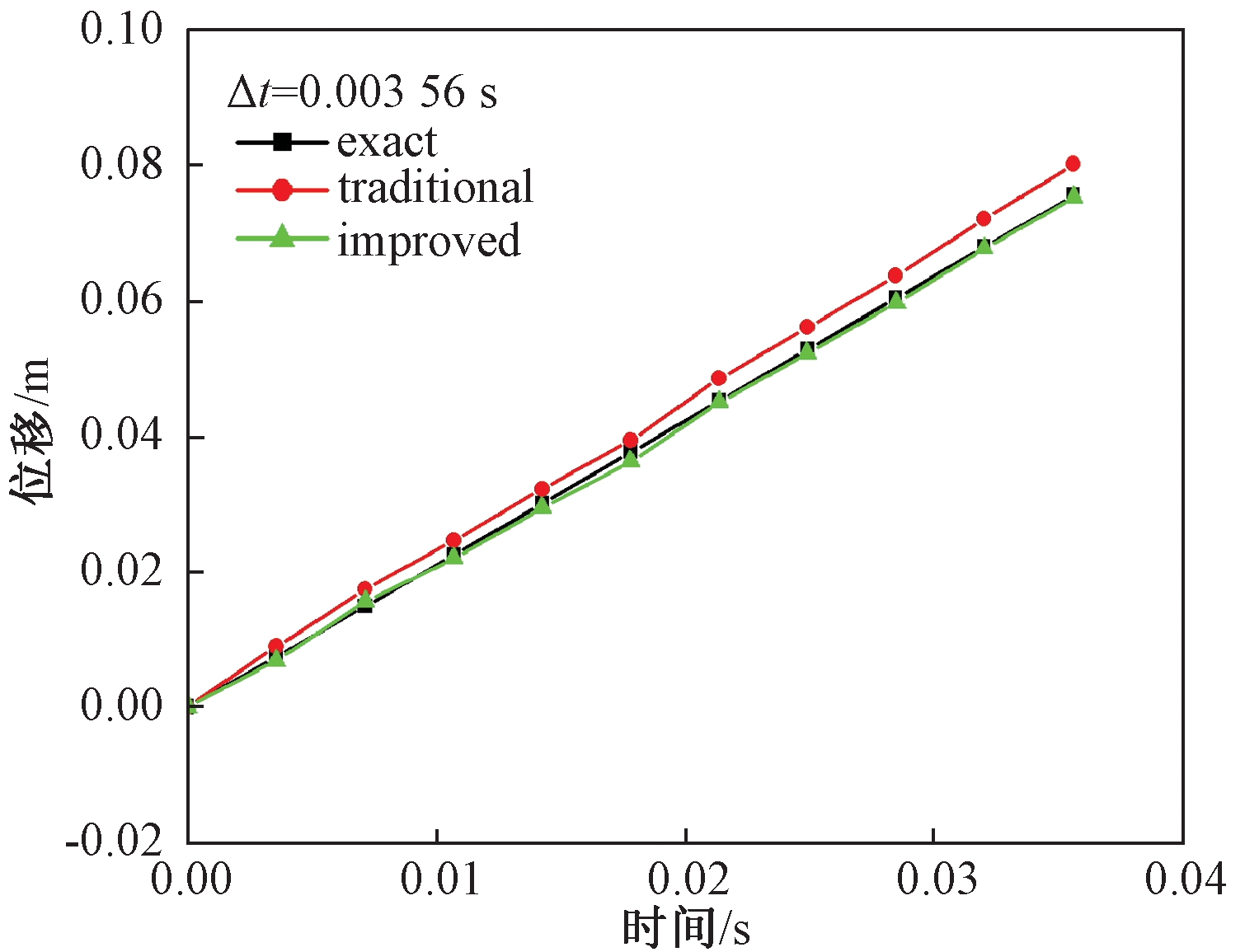
图7 Δt=0.003 56 s时改进前后结果的对比曲线
Fig.7 The comparison curves of the results before and after the improvement when Δt=0.003 56 s
将时间步长减小为原来的1/2,Δt=0.001 78 s，图8给出了该步长下改进前后计算结果的对比.从图中可以看出，改进前的结果在某些时刻会出现不稳定的现象，改进后的结果与精确解更为吻合，再次验证了本文方法的有效性.
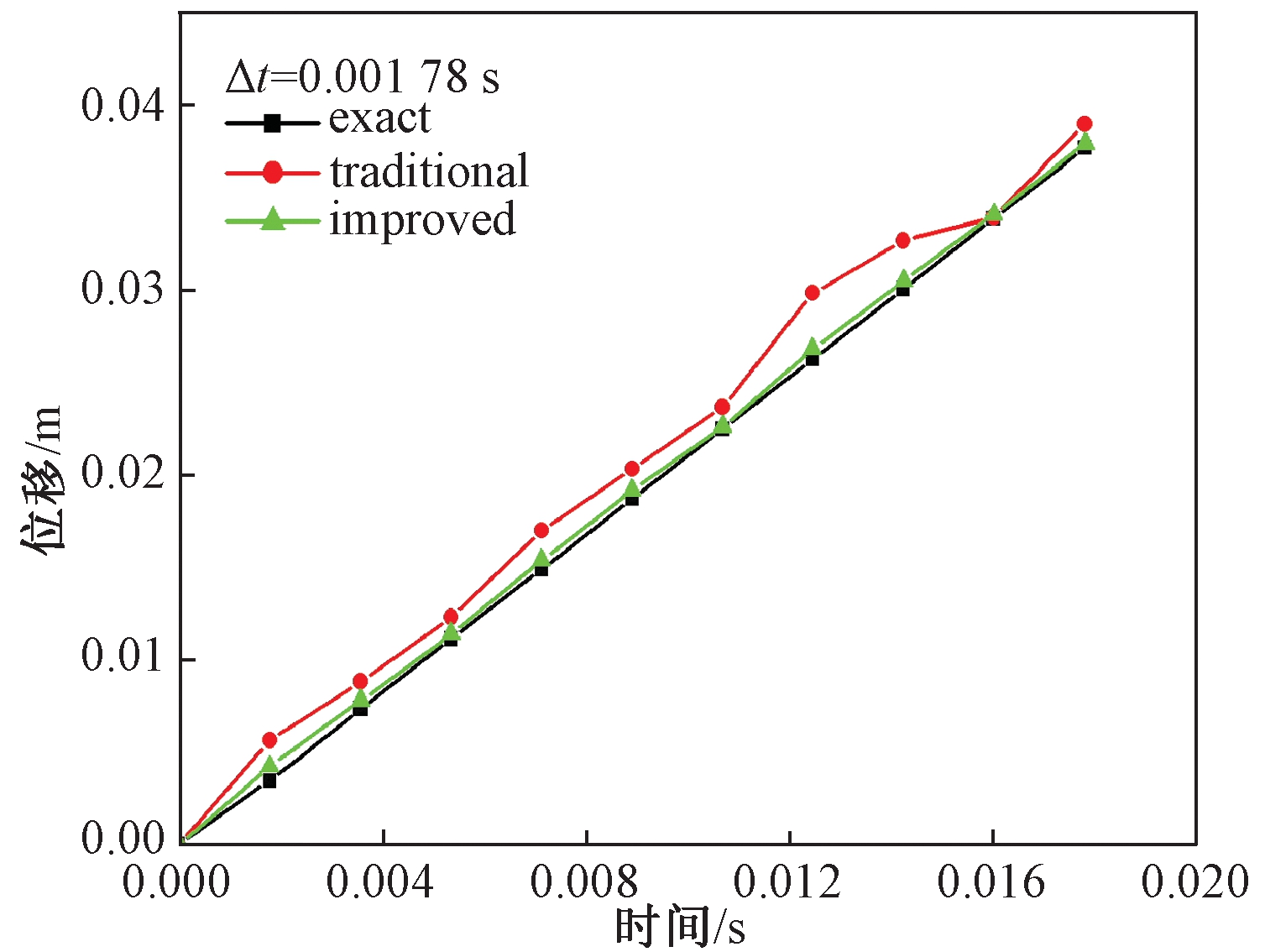
图8 Δt=0.001 78 s时改进前后结果的对比曲线
Fig.8 The comparison curves of the results before and after the improvement when Δt=0.001 78 s
3.2 带孔平板在动态载荷下的响应
该问题的分析模型如图9(a)所示，图9(a)中几何尺寸单位为mm，边界条件：下端面约束所有方向的自由度，上端面施加随时间变化的均布载荷，载荷曲线如图9(b)所示，初始时刻载荷为零，在t=3.75×10-5 s时达到最大值118.125 MPa.模型的材料参数为：弹性模量 E=6.9×104 MPa，密度ρ=2.7×10-9 kg/mm3，泊松比ν=0.3.
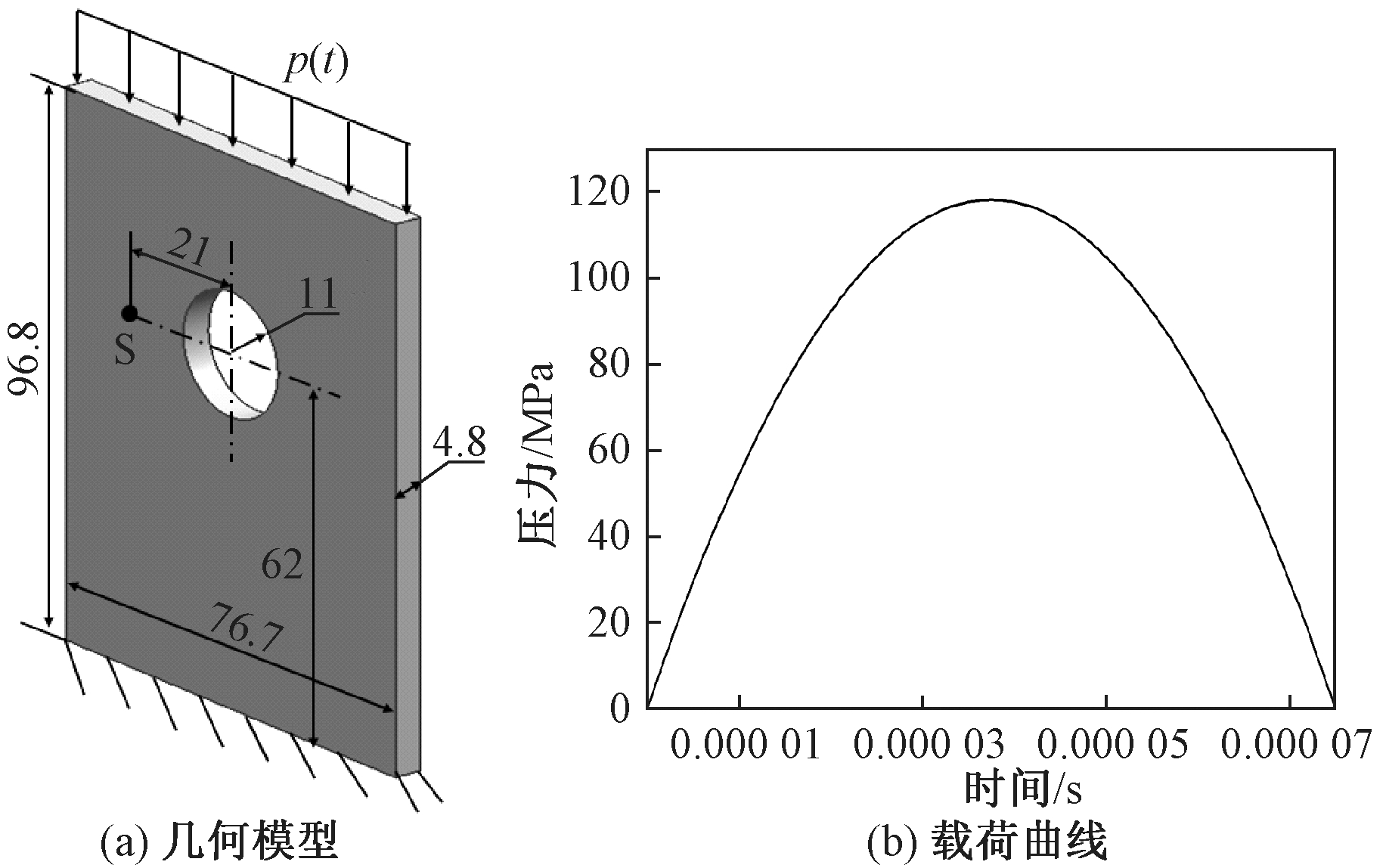
图9 带孔平板的几何模型及载荷曲线示意图
Fig.9 The geometric model and load curve of a plate with a hole
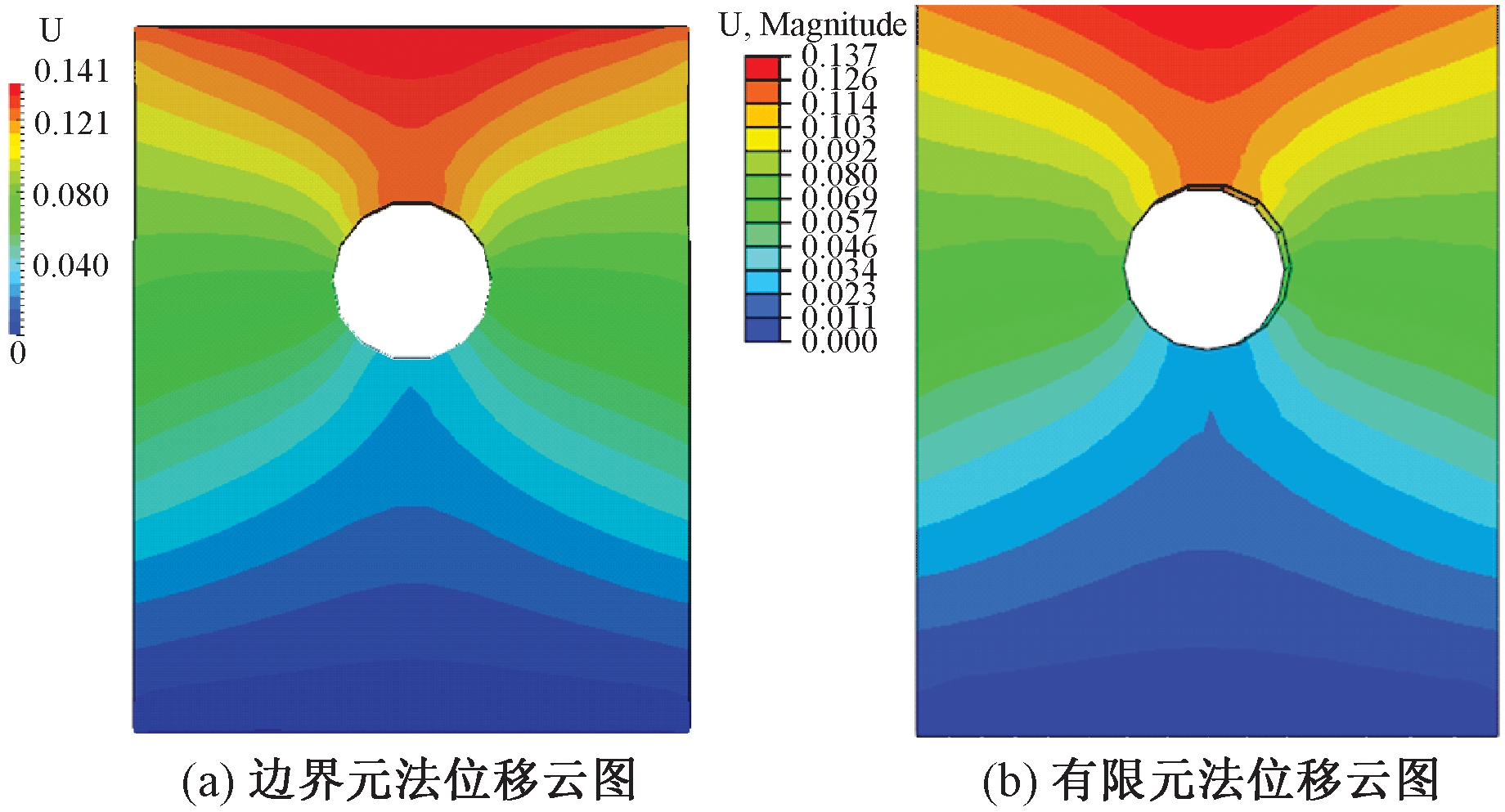
图10 t=2.5×105 s时带孔平板的位移分布云图
Fig.10 The displacement nephogram of the plate with a hole when t=2.5×105 s
采用尺寸为10 mm的线性三角形单元离散模型，该算例无解析解，将本文的计算结果与有限元分析软件ABAQUS的结果进行对比，为了得到更加准确的对比数据，将有限元网格尺寸取为5 mm.
取t=2.5×10-5 s时所有节点的位移值绘制成位移分布云图，并与有限元位移云图进行比较，如图10所示，本文方法的结果云图和有限元法基本一致，再次验证了该方法的正确性.
为了观察小孔附近的应力集中现象，根据t=2.5×10-5 s时所有节点的mises应力值绘制成应力分布云图，并与有限元结果云图比较，如图11所示，应力分布与有限元的分析结果基本一致，可以明显看出小孔附近的应力值最大.
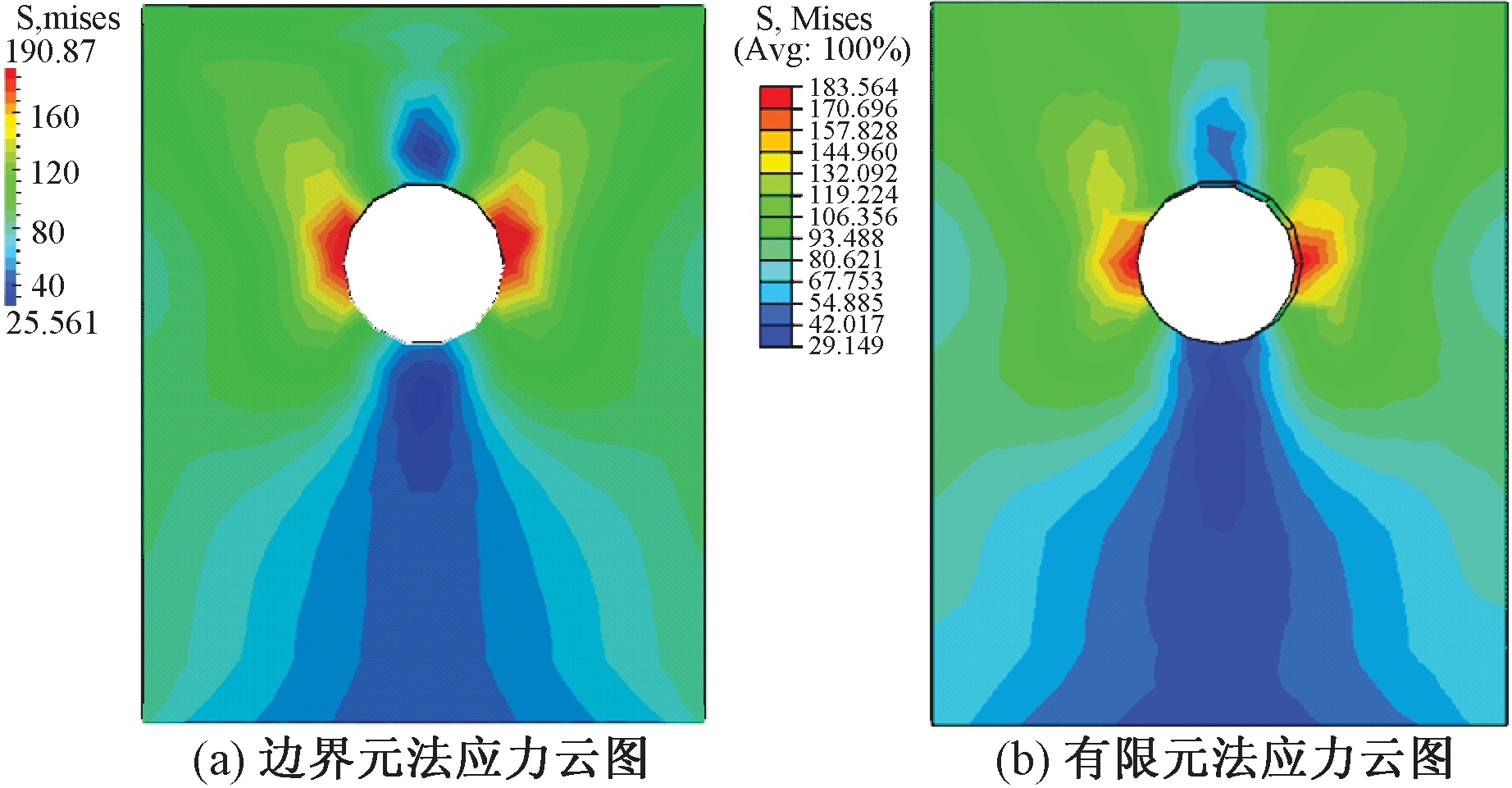
图11 t=2.5×10-5 s时带孔平板的应力分布云图
Fig.11 The stress nephogram of the plate with a hole when t=2.5×10-5 s
4 结论
笔者针对瞬态弹性动力学问题，采用时域边界元法进行数值求解，给出了该问题时域边界积分方程的一般形式.通过研究基本解函数的性质，提出了一种适用于动态问题的与时间步长相关的奇异单元细分法.在本研究中，首先由时间步长和波速计算出两个波动前沿的传播半径，然后结合源点的位置将奇异积分单元分3种情况进行细分，细分后再通过坐标变换法消除弱奇异性，刚体位移法消除强奇异性.与只考虑源点位置的传统细分法相比，该方法提高了奇异积分的精度，从而也提高了最终计算结果的精度.最后的两个算例也验证了方法的有效性，结果显示：对于存在奇异积分的第一个分析步，结果误差能够减小15.5%；利用该方法得到的仿真结果能够准确模拟位移和应力的分布与变化.
[1] 徐赫, 杨怡, 雷志鹏. 蝉翼结构静力学仿真和力学性能分析[J]. 郑州大学学报(工学版), 2017, 38(1):1-5.
[2] 李鹤龄, 王文伟, 任金秀. 广义不确定性原理下广义外势中n维理想费米气体的热力学性质[J]. 河南师范大学学报(自然科学版), 2017,45(3): 77-83.
[3] 钱振东, 张勐, 许静. 动水压力对钢桥面环氧沥青铺装裂缝扩展影响[J]. 郑州大学学报(工学版), 2016, 37(6): 48-52.
[4] 姚振汉, 王海涛. 边界元法[M]. 北京: 高等教育出版社, 2010.
[5] 胡良明, 李宗坤, 周鸿钧. 重力坝坝踵界面裂缝的地震断裂分析[J]. 郑州大学学报(工学版), 2002, 23(3): 101-103.
[6] BANERJEE P K, BUTTERFIELD R. Boundary element methods in engineering science[M]. London: McGraw-Hill, 1981.
[7] ZHANG J M, QIN X Y, HAN X, et al. A boundary face method for potential problems in three dimensions[J]. International journal for numerical methods in engineering, 2009, 80(3): 320-337.
[8] QIN X Y, ZHANG J M, LI G Y, et al. An element implementation of the boundary face method for 3D potential problems[J]. Engineering analysis with boundary elements, 2010, 34(11): 934-943.
[9] ZHANG J M, LU C J, ZHANG X X, et al. An adaptive element subdivision method for evaluation of weakly singular integrals in 3D BEM[J]. Engineering analysis with boundary elements, 2015, 51: 213-219.
[10] 周焕林, 牛忠荣, 程长征, 等. 各向异性位势问题边界元法中几乎奇异积分的解析算法[J]. 计算力学学报, 2008, 25(3):333-338.
[11] 刘兴业. 边界元法解弹性动力学问题[J]. 地震工程与工程振动, 1988, 8(4): 99-106.
[12] MANOLIS G D, BESKOS D E. Boundary element methods in elastodynamics[M]. London: Uwin Hyman, 1989.
[13] 马宏伟, 吴斌. 弹性动力学及其数值方法[M]. 北京: 中国建材出版社, 2004.