0 引言
随着我国交通事业的发展,宽幅预应力连续箱梁桥的应用越来越广泛[1-3]。然而对于宽箱梁而言,截面会表现出较为明显的剪力滞效应,不宜继续使用平截面假定分析截面的正应力状态[4],同时,连续箱梁多采用悬臂施工,主梁截面正应力最大状态发生在施工阶段而非成桥阶段,在剪力滞效应的影响下,可能发生施工过程中的安全事故[5]。因此,研究宽幅箱梁悬臂浇筑施工过程中的剪力滞效应就显得尤为重要。
已有文献指出,对于一般悬臂施工的箱梁桥,随着施工阶段的进行,主梁宽跨比逐渐减小,剪力滞效应也逐渐减弱[6-9]。但是,上述研究所列正应力横向分布往往是多种荷载如自重、已张拉预应力束等共同作用的结果,并非单个施工步骤如混凝土浇筑、预应力钢束张拉所引起的正应力,故难以明确结构在上述单一荷载作用下的剪力滞效应以及其随施工阶段的变化。因此,以某宽幅梁桥施工过程为背景,研究混凝土浇筑、张拉预应力钢束以及合龙等单个施工步骤引起的正应力横向分布特征及其随施工过程的变化影响。
1 工程背景及有限元模型
1.1 工程背景
本桥为(45+61+61+45)m预应力混凝土连续箱梁桥,桥宽26.5 m。主墩和跨中处梁高分别为3.0 m和1.5 m,梁高采用二次抛物线变化。下部结构采用箱型墩,柱式桥台,钻孔灌注桩基础。主梁及调平层为C50混凝土;盖梁、立柱、桥墩为C30混凝土。
桥梁纵向预应力体系采用高强度低松弛钢绞线,张拉控制应力均为σcon=0.75fpk。桥梁跨径、悬臂根部截面形式及部分钢束布置如图1所示。
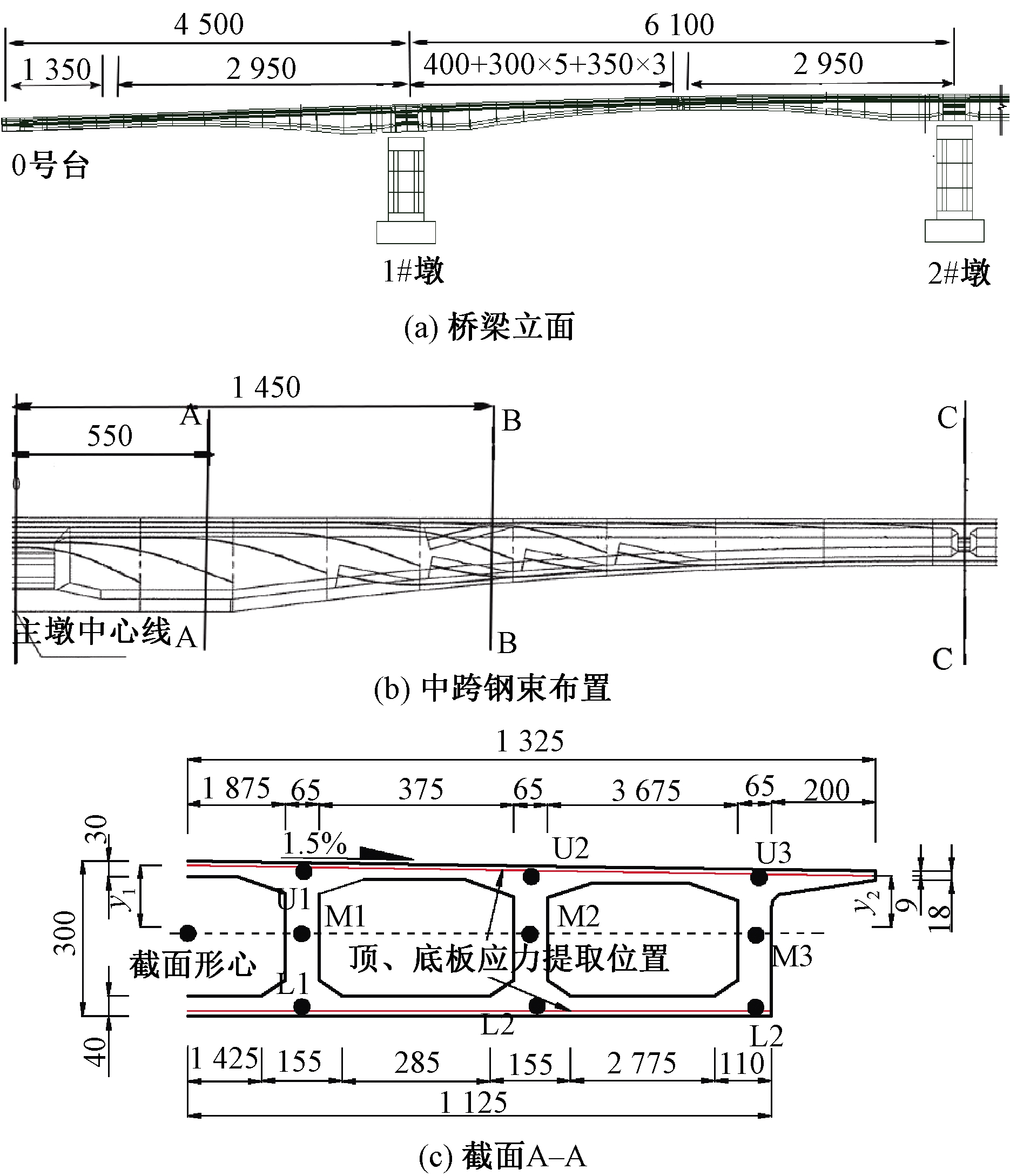
图1 桥梁概况(单位:cm)
Figure 1 Situation of the bridge(unit: cm)
本桥采用悬臂浇筑施工:0#块与1#块在桥墩与临时支撑上进行支架施工;2#块至8#块均为挂篮施工,主要包含混凝土浇筑和钢束张拉2个加载步骤;合龙顺序为先边跨再中跨,同样选用挂篮合龙;中跨合龙完成后再拆除临时固结。
1.2 有限元模型
采用Midas/FEA实体单元建立有限元模型对施工过程进行仿真模拟。考虑计算精度与计算成本,在应力提取位置网格尺寸为15 cm,远离应力提取位置网格尺寸为50 cm。用悬臂端最外侧位置节点荷载的激活与钝化模拟混凝土浇筑的湿重;通过Midas/Civil模型导入钢束并施加预应力荷载。悬臂施工以及合龙阶段的边界条件为临时固结,通过约束支座位置梁底节点三向平动自由度的方式进行模拟(图2(a));体系转换和成桥阶段的边界条件为永久支座,通过约束支座位置附近节点相应自由度进行模拟(图2(b))。主梁最大悬臂状态模型如图3所示。为验证模型的正确性,还采用Midas/Civil建立梁单元模型进行对比,由结果可知,2个模型所得结构施工过程中的内力和位移结果有良好的一致性。
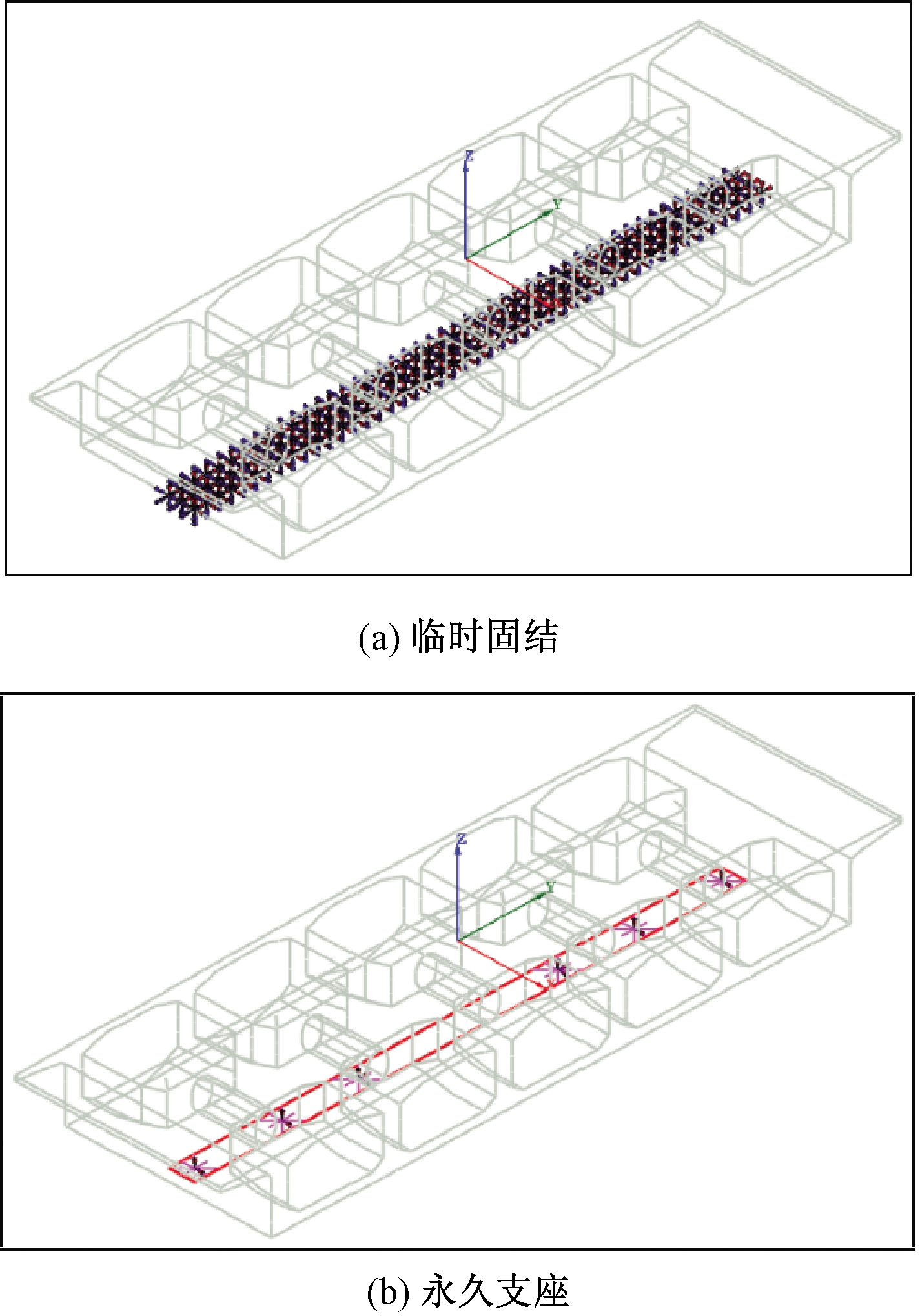
图2 支座模拟
Figure 2 Simulation of bridge bearing
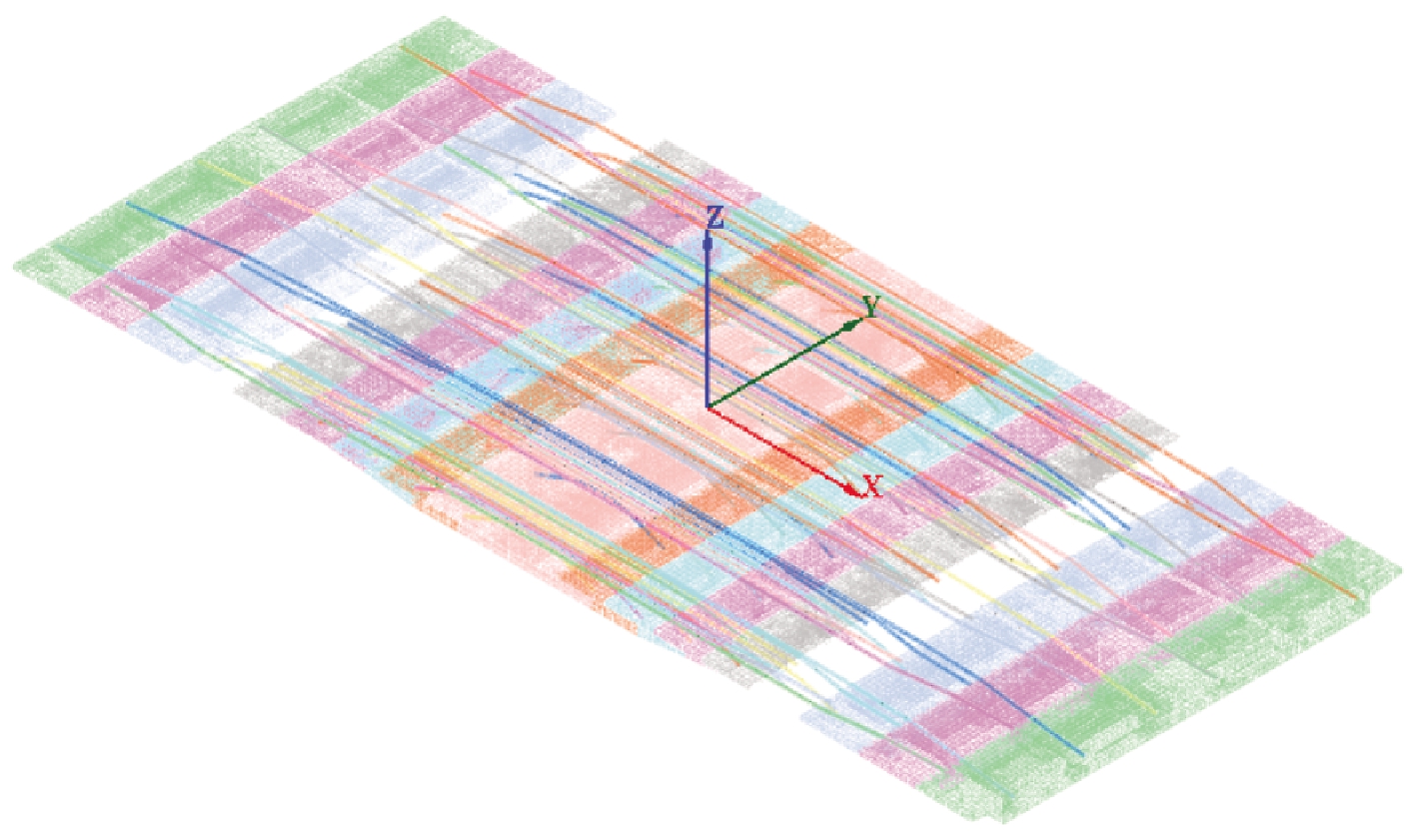
图3 最大悬臂状态Midas/FEA模型
Figure 3 Midas/FEA model of the biggest cantilever stage
2 计算结果分析
在悬臂施工过程中,根部截面正应力最为显著,但为避免临时固结对截面正应力分布的影响,选取2#墩右侧1#块内截面A为关键截面进行分析,其截面尺寸和顶底板正应力提取位置见图1。为获得混凝土浇筑及预应力钢束张拉单独作用下的截面正应力,分别提取各阶段混凝土浇筑和预应力钢束张拉前后的正应力值,前后相减即得此施工步骤单独引起的正应力。合龙时情况较为复杂,合龙束张拉以及体系转换是各主梁截面正应力发生变化的主要步骤[10],故此阶段主要分析合龙束张拉与体系转换引起的正应力变化。并且,合龙时整个主梁发生内力重分布,不同截面正应力变化规律有差异,因此,除截面A外,另选取跨中1/4截面B与跨中截面C(图1(b))分析合龙引起的正应力变化。
2.1 浇筑混凝土的影响
图4给出了浇筑引起的截面A顶板正应力,结合图6的底板应力可知,不同梁段的浇筑均分别对截面顶底面产生拉应力和压应力,且浇筑位置距截面A位置越远,混凝土湿重荷载的力臂越大,应力幅值也越大,符合悬臂梁受力特征。
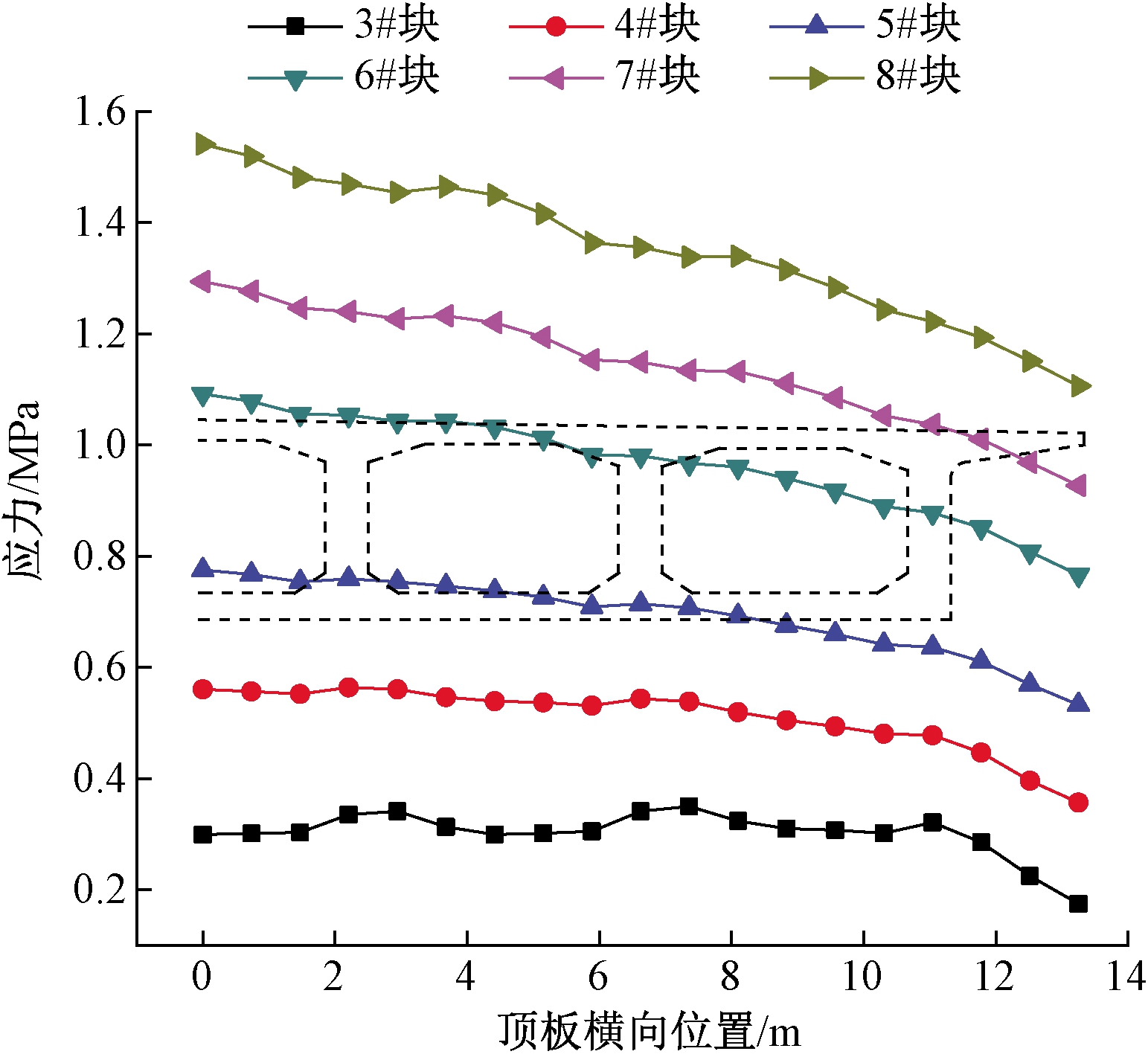
图4 浇筑引起的截面A顶板正应力横向分布
Figure 4 Normal stress in the roof of section A caused by concrete pouring
各梁段的浇筑在顶板产生的正应力横向分布规律并不一致。3#块浇筑引起的应力沿横向分布呈波浪状,腹板位置出现应力幅值的波峰,远离腹板位置则为波谷,这样的规律实际是各个腹板自身正剪力滞效应的体现。另外,翼缘范围内的应力幅值则明显偏小。6#~8#块由浇筑引起的正应力在整个顶板范围内表现出从中间向两侧逐渐减小的趋势,从箱梁中心到边缘的应力差值达到0.4 MPa,并且此现象并非截面横坡造成的:6#~8#块由浇筑引起的中心位置和翼缘板边缘的应力比分别为1.42、1.40、1.40,而2个位置到截面形心点竖向距离(图1(c)中y1与y2)比值仅为1.14。这实际上是宽幅多室箱梁各腹板受力不一致的表现,表1给出了不同梁段浇筑引起A截面形心轴与腹板交点位置(图1(c)M1~M3)的剪应力,可以看出,随着施工阶段的进行,中间腹板的剪应力明显大于边腹板。这种因各腹板剪应力差异而导致的顶板正应力分布特征可称之为此箱形截面的“整体”剪力滞效应,且为正剪力滞效应。各腹板剪应力的横向分布不均也是宽体箱梁的主要受力特征之一,同时,正应力在腹板附近位置仍有轻微波动,但在腹板位置近似出现正应力的波谷,这与悬臂箱梁端集中荷载作用下产生正剪力滞效应的传统认知相悖。
表1 浇筑引起各腹板位置的剪应力
Table 1 Shear stresses at different webs caused by concrete pouring
MPa
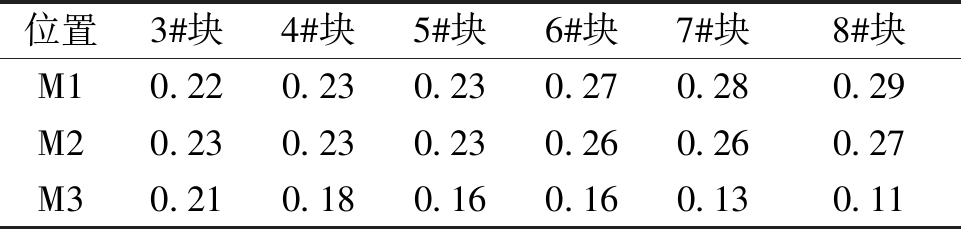
位置3#块4#块5#块6#块7#块8#块M10.220.230.230.270.280.29M20.230.230.230.260.260.27M30.210.180.160.160.130.11
针对此现象,图5给出了不同腹板数量的悬臂梁在梁端集中荷载作用下根部截面正应力分布。可以看出,随着腹板数量增加,整个截面正应力的横向分布逐渐趋于均匀,但截面的“整体”剪力滞效应相对愈加明显,而腹板自身位置的正剪力滞效应则不断减弱。在腹板数量较多时,相对明显的“整体”正剪力滞效应和微弱的腹板正剪力滞效应的叠加,使正应力横向波动的波峰不再位于腹板处,从而使腹板位置看似呈现负剪力滞效应。
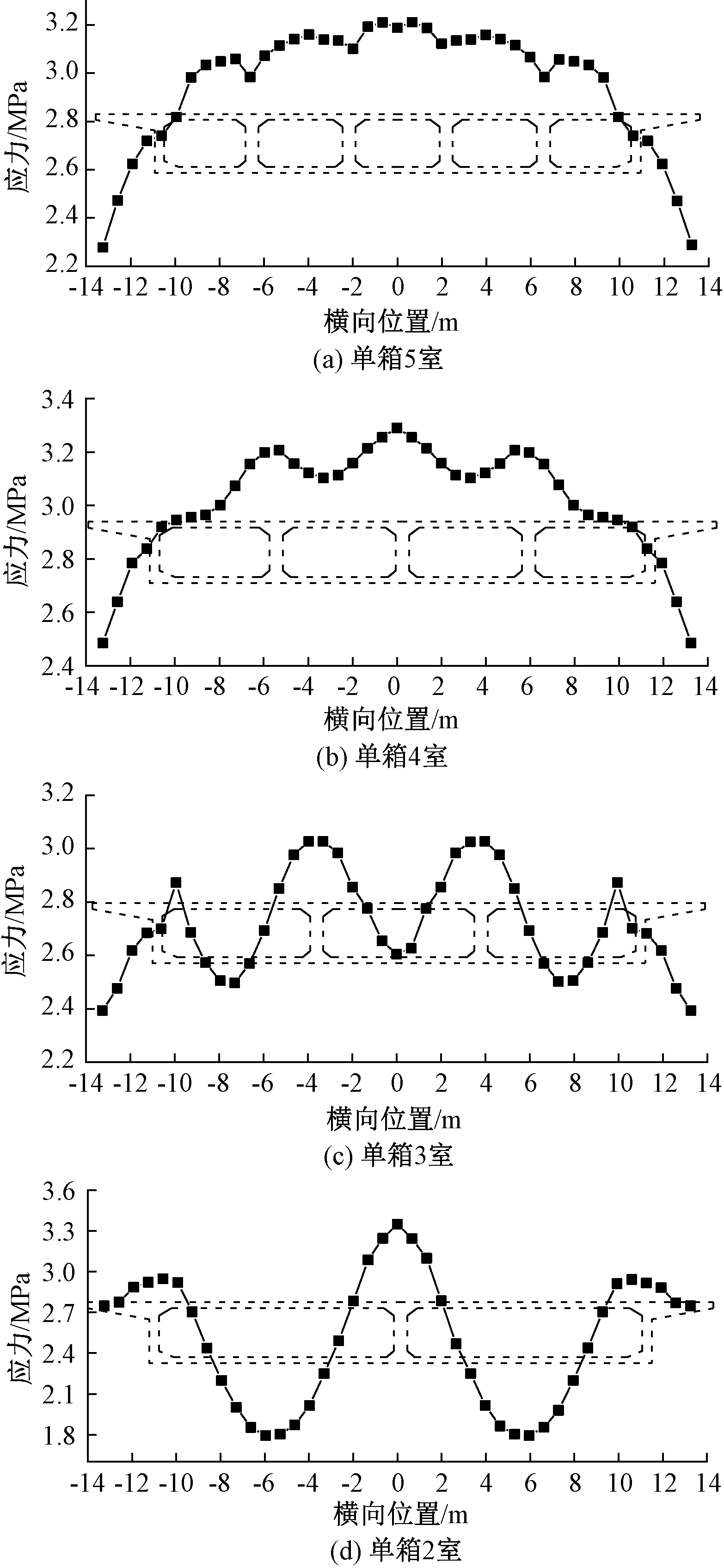
图5 不同腹板数量主梁顶板正应力分布
Figure 5 Roof normal stresses of different box girders
实际上,上述“整体”和“局部”效应在其他针对宽体多室箱梁成桥阶段的分析中亦有表现,如文献[11-12],都被笼统称之为剪力滞效应。但从上文分析可知,两者的成因和受宽跨比的影响并不一致,应有所区分。另外,浇筑4#块、5#块的结果处于3#块和6#块之间。
由此可以认为,混凝土浇筑或者说端部集中荷载作用在根部截面产生的剪力滞效应可以视为“整体”和“局部”两种效应的叠加:距离截面位置越近,也即悬臂长度较小时,浇筑产生的正应力更多地表现出腹板自身的“局部”剪力滞效应;随着悬臂长度的增加,则主要表现出整个箱形截面的“整体”剪力滞效应,并且均为正剪力滞效应;只是在悬臂长度较大时,2种效应的叠加使腹板位置近似出现正应力的波谷。
为评价“整体”剪力滞效应随荷载和施工阶段的变化并为屏蔽局部效应的影响,定义参数μ作为“整体”剪力滞效应的量化指标如式(1)所示,计算出各阶段顶底板μ值列于表2。
(1)
式中:σ1、σ3分别为箱梁顶底板中间腹板和边腹板位置(图1中U1、L1和U3、L3)的正应力值;![]() 为二者平均值。
为二者平均值。
从表2可以看出,在截面顶板,混凝土浇筑引起的截面“整体”剪力滞效应随宽跨比B/L的减小而增加,且当B/L达到1.39时趋于稳定。
表2 截面A整体剪力滞效应
Table 2 Global shear lag effect of section A
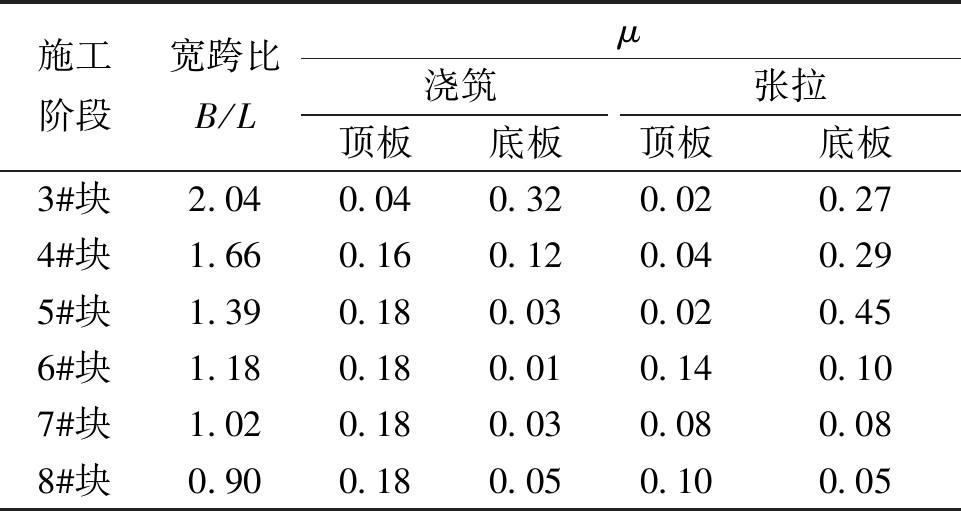
施工阶段宽跨比B/Lμ浇筑张拉顶板底板顶板底板3#块2.040.040.320.020.274#块1.660.160.120.040.295#块1.390.180.030.020.456#块1.180.180.010.140.107#块1.020.180.030.080.088#块0.900.180.050.100.05
对于底板的正应力横向分布,从图6和表2可以看出,各阶段浇筑所引起的正应力横向分布基本均匀,而3#和4#块浇筑过程中较大的μ值源于极小的正应力幅值。各施工阶段,腹板位置均表现出极微弱的“局部”正剪力滞效应。但对于“整体”剪力滞效应,当B/L较大时,在边腹板处引起的正应力幅值偏小,即表现出“整体”负剪力滞效应。总体来说,混凝土浇筑对底板的剪力滞效应较小,可以忽略。
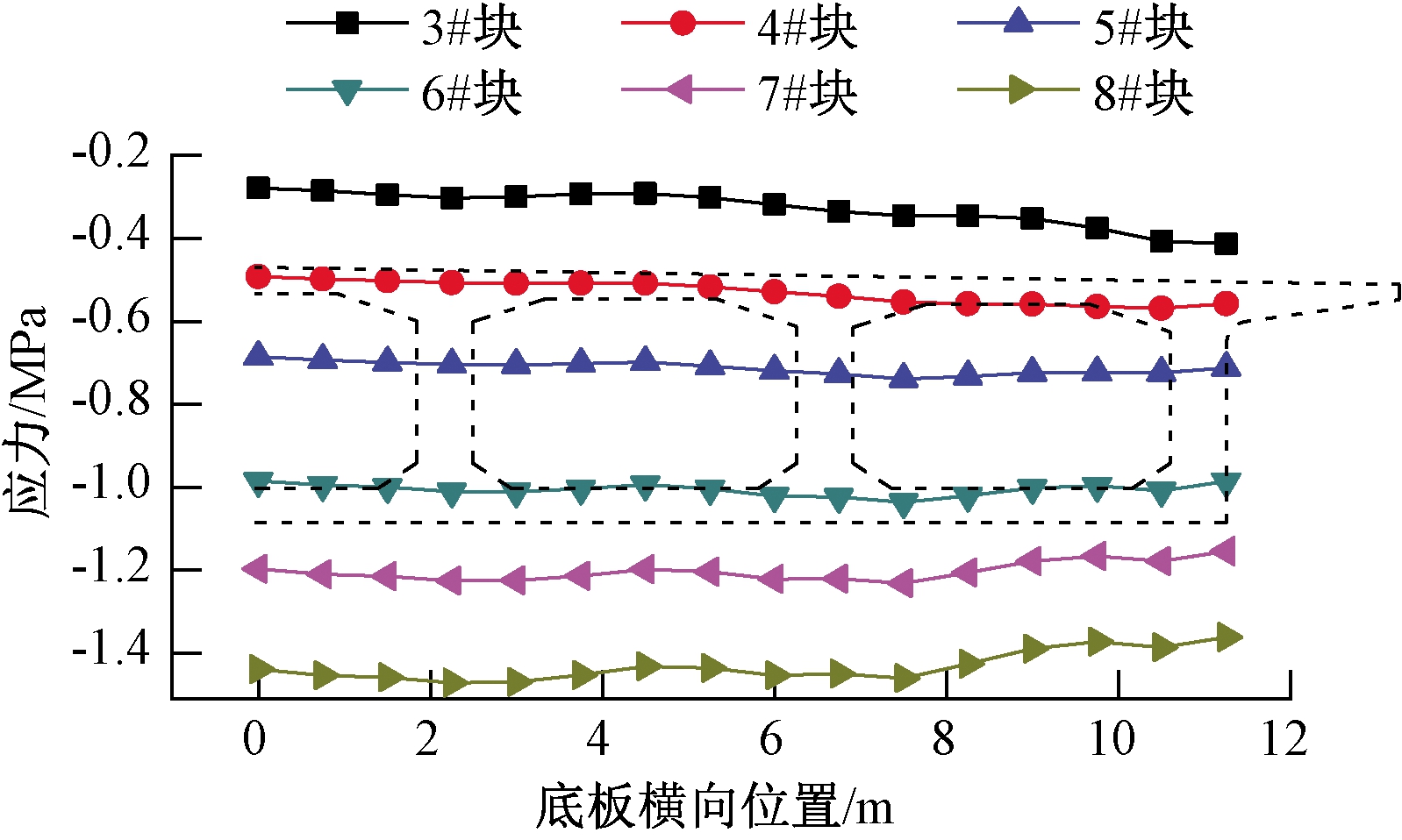
图6 浇筑引起截面A底板正应力横向分布
Figure 6 Normal stress in the bottom plate of section A caused by concrete pouring
2.2 钢束张拉影响
钢束张拉相当于在悬臂端施加偏心轴力[13],在梁体中产生轴力弯曲联合作用,对截面A顶底板分别产生压应力和拉应力,且应力幅值大小与所张拉的预应力钢束数量与偏心距有关。
对于顶板应力,从图7可知,在张拉3#~5#块钢束过程中,箱室范围内的正应力分布相对较为均匀,但依然同时表现出箱梁截面微弱的“整体”正剪力滞效应和腹板自身较明显的“局部”负剪力滞效应,两侧翼缘板的正应力幅值则明显偏小;在张拉6#~8#块过程中,整个截面的正应力表现出从中间向两侧逐渐减小的规律,即“整体”正剪力滞效应,此时的“局部”剪力滞效应不再明显。同样,“整体”剪力滞效应随施工阶段的变化亦可从表2的μ值得以体现。

图7 张拉引起截面A顶板正应力横向分布
Figure 7 Normal stress in the roof of section A caused by prestressing
对于底板正应力,从图8可知,各施工阶段预应力张拉在底板引起的拉应力幅值较小,但在横向有较为明显的波动,尤其在悬臂长度较小时。这种正应力横向分布依然是“整体”和“局部”剪力滞效应的综合表现,均为正剪力滞效应,并且受到正应力幅值与B/L的影响,从表2亦可得到印证。
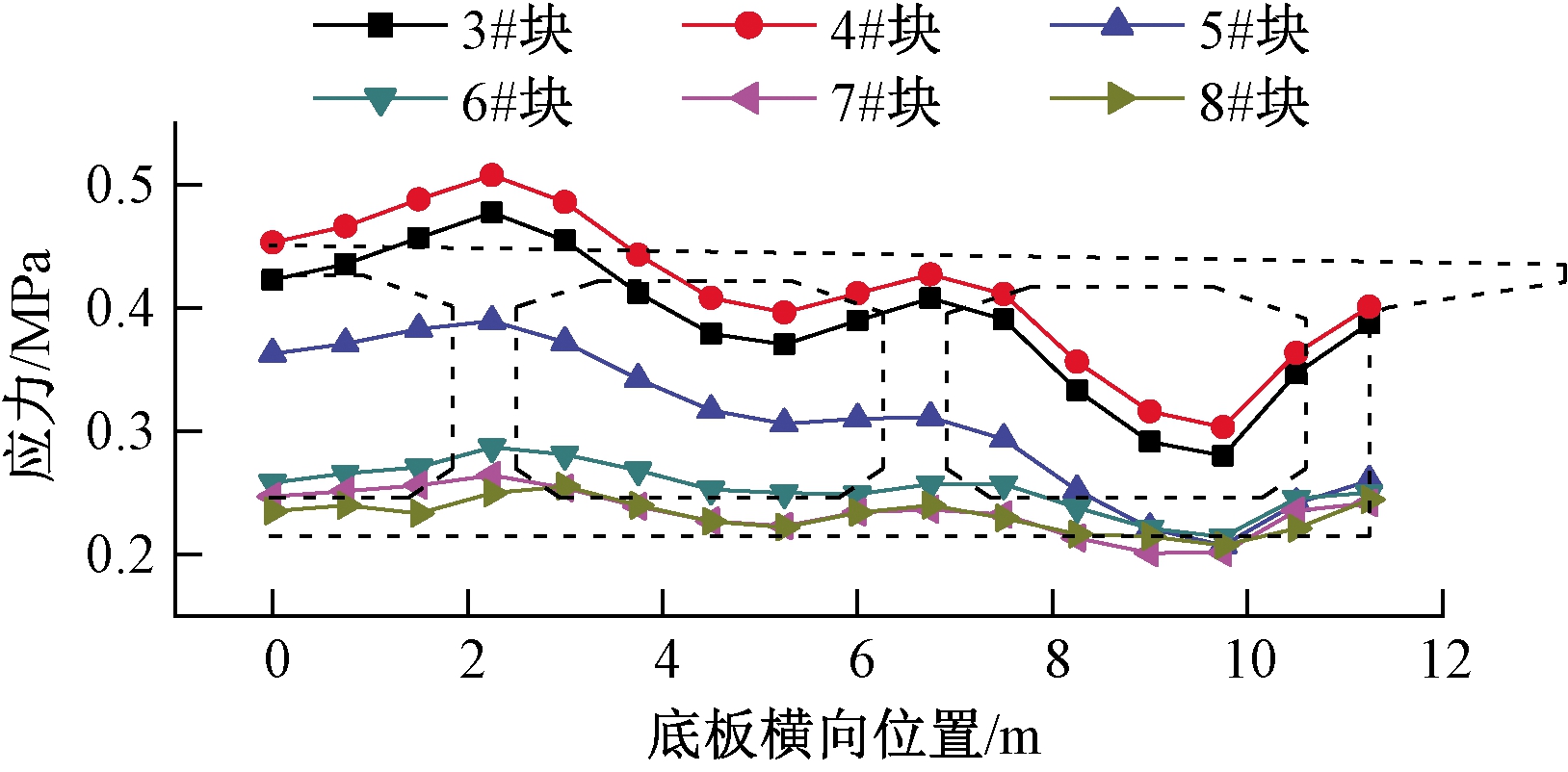
图8 张拉引起截面A底板正应力
Figure 8 Normal stress in the bottom plate of section A caused by prestressing
对比混凝土浇筑和钢束张拉2个施工步骤,在悬臂施工阶段,两者在根部截面所引起的剪力滞效应主要体现在顶板,前者底板正应力均匀而后者底板正应力幅值较小。随着施工的推进,整体剪力滞效应愈加凸显而局部剪力滞效应逐渐减弱。此外,混凝土浇筑较钢束张拉所引起的整体剪力滞效应更为明显,这是由于前者在截面仅产生弯矩效应,而后者是轴弯联合作用,轴向应力的存在可能使应力横向分布趋向均匀。
2.3 合龙的影响
2.3.1 张拉合龙束
张拉合龙束的过程相当于在两端依然临时固结的梁体中部区域施加偏心轴力,引起的3个关键截面顶底板正应力横向分布如图9所示。除截面B顶底板以及截面A底板正应力幅值较小而分布略显均匀外,其他截面顶底板的正应力依然有“整体”和“局部”剪力滞效应:截面A顶板主要表现出“整体”正剪力滞效应,而截面C的顶底板则同时表现出“整体”和“局部”的正剪力滞效应。“局部”剪力滞效应在截面C较为明显而截面A不明显的原因,则可能是合龙束穿过截面C而未穿过截面A。
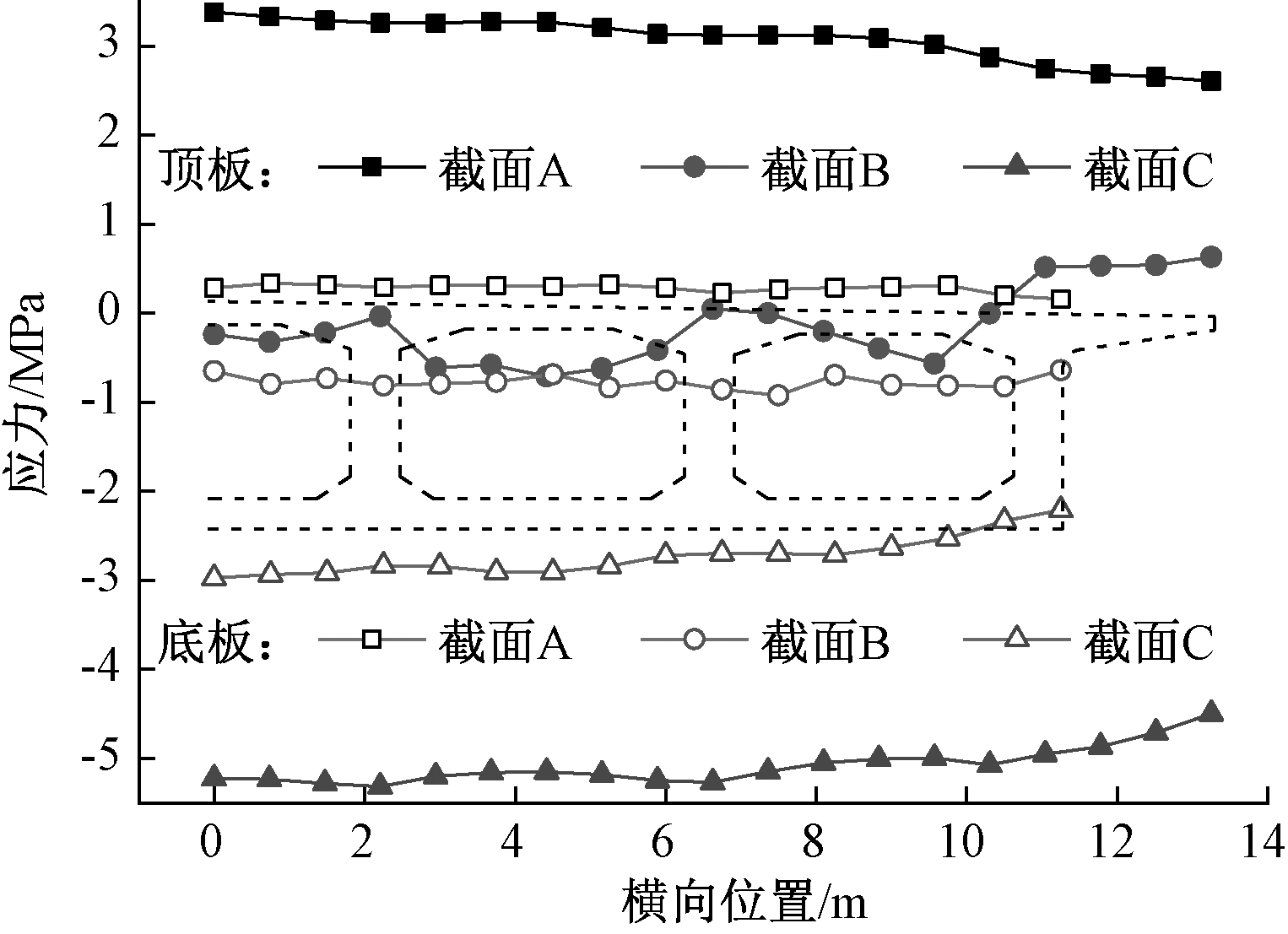
图9 张拉合龙束引起截面正应力横向分布
Figure 9 Normal stresses in section A caused by closure prestressing
2.3.2 体系转换的影响
从图10可以看出,体系转换在3个关键截面产生的正应力横向分布在顶板同样表现为“整体”和“局部”剪力滞效应,但各有正负:“整体”剪力滞效应在截面A、B表现为正效应而在截面C则表现为负效应,并且“局部”剪力滞效应在3个截面均为负效应;在截面底板,截面B、C正应力分布较为均匀,但截面A依然有明显的“整体”正剪力滞效应。
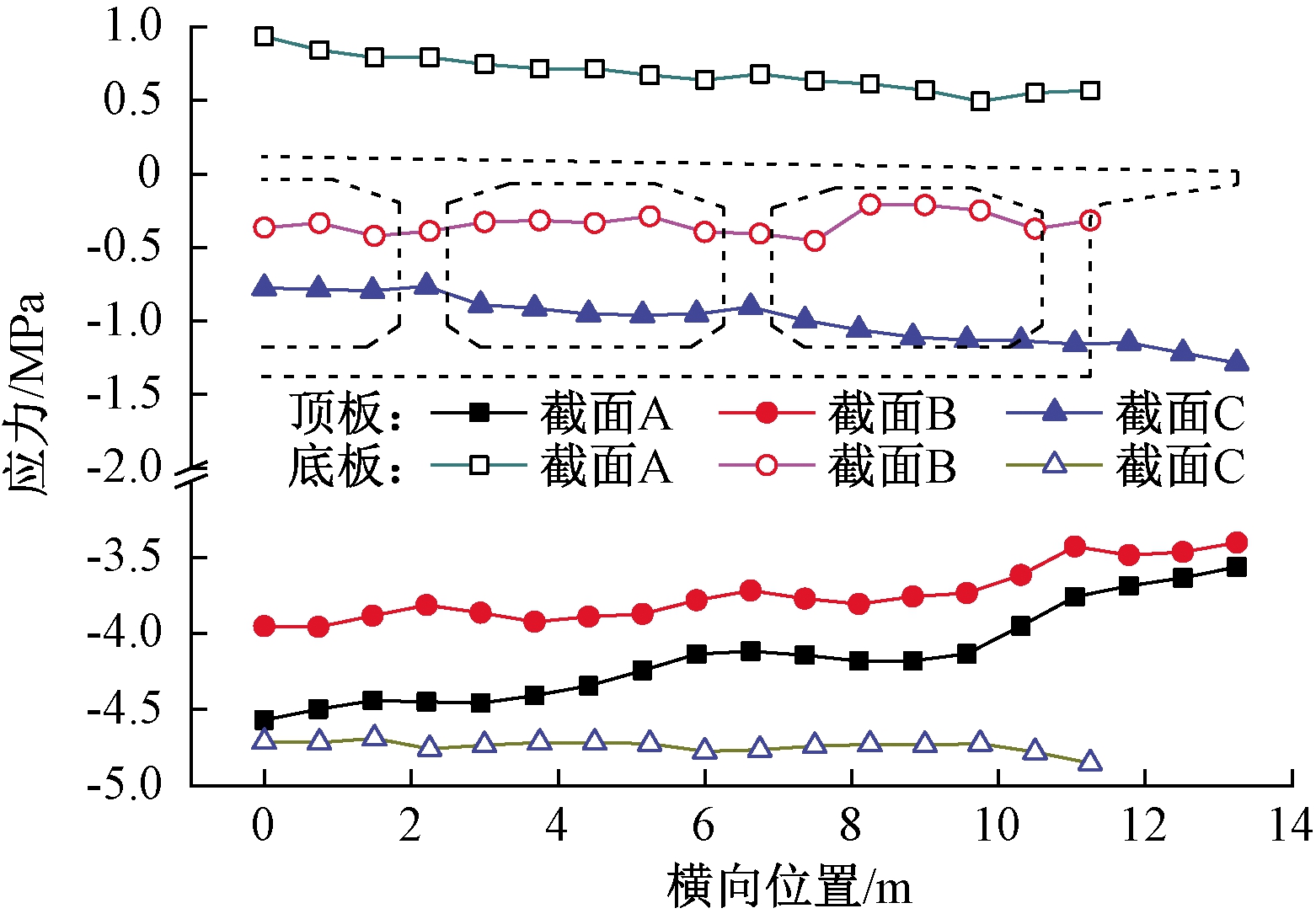
图10 体系转换引起截面顶板正应力
Figure 10 Normal stresses in section A caused by system transformation
3 结论
为明确多室箱梁在悬臂浇筑和合龙过程中的剪力滞效应,对单个施工荷载作用下特征截面正应力横向分布以及其随施工阶段的变化进行了分析,研究发现:
(1)多室箱梁的截面剪力滞效应可以分解为截面“整体”剪力滞效应和各腹板自身局部剪力滞效应,并且随着箱室数量的增加,“整体”效应相对渐趋明显而“局部”效应相对减弱。整体剪力滞效应是各腹板剪应力横向分布不均匀的表现,这也是宽体箱梁的主要受力特征之一。
(2)在悬臂施工阶段,不同施工荷载如混凝土浇筑和钢束张拉在根部截面所引起的剪力滞效应主要体现在顶板,并且随着施工阶段的进行及B/L的减小,“整体”剪力滞效应愈加凸显而“局部”剪力滞效应逐渐减弱。另外,混凝土浇筑较钢束张拉所引起的“整体”剪力滞效应更为明显。
(3)不仅在悬臂施工阶段,对于合龙过程,两个施工步骤所产生的剪力滞效应同样可以分解为“整体”和“局部”效应,在成桥阶段的受力分析中同样如此。因此,对于箱梁的剪力滞效应,应根据箱室数量、桥宽和宽跨比等参数区分这两种效应的权重并有针对性地进行分析。
[1] 杨柄楠.宽幅箱梁桥施工监控和剪力滞效应分析[D].郑州:郑州大学,2017.
[2] 包启航.宽幅箱形梁桥设计与计算方法研究[J].城市道桥与防洪,2017(11):62-65,10.
[3] 李宇,杨赐,李琛,等.大跨连续梁桥施工膺架的设计研究[J].郑州大学学报(工学版),2016,37(2):77-81.
[4] 项海帆.高等桥梁结构理论[M].2版.北京:人民交通出版社,2013.
[5] 丁艳超.PC箱形截面连续刚构桥施工阶段剪力滞效应分析[D].重庆:重庆交通大学,2014.
[6] 蔺鹏臻.混凝土箱梁剪力滞效应的分析理论与应用研究[D].兰州:兰州交通大学,2011.
[7] 王金周.单箱三室预应力混凝土连续宽箱梁桥剪力滞效应分析[D].西安:长安大学,2015.
[8] 雒敏,蔺鹏臻.单箱三室箱梁剪力滞效应的试验研究[J].实验力学,2015,30(5):621-628.
[9] 罗金山.悬臂箱梁桥剪力滞效应影响因素研究[D].西安:长安大学,2009.
[10] 徐培培.预应力混凝土连续箱梁悬臂施工过程中的剪力滞效应研究[D].北京:北京交通大学,2014.
[11] 王雷.现浇中小跨径连续单箱多室宽箱梁桥空间效应研究[D].北京:北京交通大学,2013.
[12] 李晨翔,刘艳芳.异形混凝土宽箱梁桥计算方法研究[J].中国勘察设计,2016(10):98-101.
[13] 蔺鹏臻,刘应龙,孙理想,等.预应力作用下简支箱梁桥的剪力滞效应分析[J].铁道工程学报,2014,31(11):54-58,76.