0 引言
最优化问题与人们的生产生活密切相关.一个最优化问题可以描述为:
其中，X=［x1，x2，…，xD］是可行域Ω中的D维决策变量；f(X)是目标函数.优化问题可以是最大化问题或是最小化问题.随着现实中最优化问题复杂度的增加，传统的借助微分学、变分法等数学工具进行逻辑推理分析获得解析解的方式不再适用，而自然启发式算法异军突起，逐渐成为求解最优化问题的核心力量［1-2］.其中，人工免疫算法受生物免疫系统免疫机制启发，在学术界和工业界受到关注并得到广泛应用［3］.
克隆选择算法是人工免疫算法在最优化领域应用最为广泛的代表性算法之一.它来源于对B细胞自适应免疫反应的原理抽象，主要包括克隆、超变异和选择3个算子.
虽然克隆选择算法被广泛应用到实践中，但随着优化问题复杂度的增加，比如多峰、旋转、复合以及高维等，克隆选择算法往往会遭遇早熟收敛和易陷入局部最优的缺点.针对这些缺点，国内外学者对克隆选择算法做出了各种改进，并在各自领域取得了很好的应用成果.高斯和柯西变异策略被引入到克隆选择算法中构造了一个快速克隆算法［4］.焦李成等［5］把量子学的思想与免疫机制相结合，提出了量子启发式重组算子和量子变异算子，并提出了受量子启发的免疫克隆算法，应用在最优化问题上.公茂果等［6］把拉马克学说应用在克隆选择算法上构造了相应的基因重组和变异算子，并提出了拉马克克隆选择算法.文献［7］提出了适应性Lévy变异算子，并通过实验证明了该变异算子在解决多峰函数时比高斯和柯西变异效果好.文献［8］将免疫克隆算法和粒子群算法结合以加强算法的性能，正交实验被引入到克隆选择中解决函数优化问题［9］，实验证明该算法能够有效保持种群多样性，避免算法不成熟收敛.针对传统算法全局搜索效率降低的问题，文献［10］提出了模糊非基因信息记忆的双克隆选择算法提高全局搜索速度和精度.文献［11］引入了粗糙集中的核值概念，提出了一种基于粗糙集核值的克隆选择算法以提升算法的收敛速度、抗体多样性和避免早熟.通过文献检索发现，混合免疫克隆选择算法通过引入新的策略和克隆选择算法改进自身算子成为现阶段研究和应用的重要方向.
笔者提出了一种混合的免疫克隆选择算法，该算法通过引入免疫重组算子来提升种群的多样性，并提出了成功历史自适应免疫超变异算子来促进算法收敛能力.通过全局搜索与局部搜索的平衡，达到寻求全局最优的目的.
1 克隆选择算法
根据克隆选择学说［12］，文献［13］最早提出了克隆选择算法CLONALG，并应用到字母识别、多模函数优化、组合优化等问题上，奠定了免疫克隆选择算法的基础.基本的克隆选择算法主要包含3个算子，分别是克隆、超变异和选择.根据克隆选择学说，其克隆产生的子代的数量与父代的适应度值成正比，而变异率与父代的适应度值成反比.在克隆选择算法的具体实施过程中，高斯变异是最常用的变异方法，但是研究表明，其搜索过程具有一定的盲目性，且收敛精度不高.另外，克隆选择算法依靠克隆大量的子代提供候选解，往往需要消耗很多的计算资源，限制了实际应用.
2 笔者提出的算法
2.1 基因重组策略
除克隆选择以外，基因重组在B细胞的免疫反应中也充当了重要的角色.免疫B细胞分化过程中，通过基因库中基因片段在DNA级别上组合生成不同的B细胞实现了抗体基因的多样化.文献［14］研究了B细胞的Y型抗体结构，提出了基因重组策略，其子代产生的方式为:
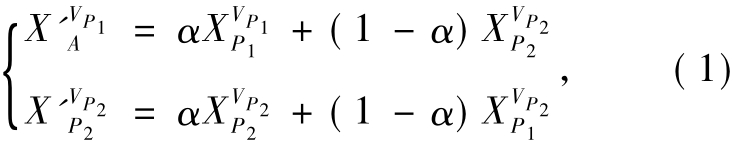
式中:XP1和XP2是随机选择的父代；VP1和 VP2是随机选择的 m 维，m∈［1，D］；α∈ (0，1)是服从均匀分布的随机数.在实施过程中，考虑到随着种群的收敛，种群中个体的相似度越来越高，这时种群内部的信息融合已不能满足多样性的需求，所以笔者将生成的子代中表现不好的个体存储在集合Archive中，在实施基因重组时，XP1取自当前种群，而 XP2则从当前种群和集合 Archive的并集中随机选取.通过这种改进，可以缓解种群收敛对多样性缺失造成的影响，提高算法的寻优能力.
2.2 成功历史自适应克隆选择
文献［15］提出了基于成功历史的自适应差分进化算法解决全局优化问题.笔者将成功历史自适应策略与克隆选择算法相结合，提出了成功历史自适应克隆选择算法.
(1)克隆:每个父代个体 Xi产生 Nc个子代
(2)成功历史自适应超变异:每个克隆个体有 M 维发生变异［16］:
其中，f*(Xi)∈［0，1］是归一化的适应度值；ρ是衰变常数，这里采用的变异策略隐式服从克隆变异的变异率与适应度成反比的规则.每个个体经历如下的变异操作
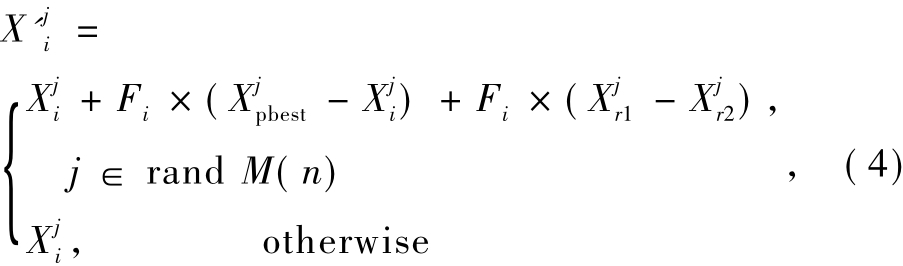
式中: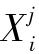
是第i个个体的第j维
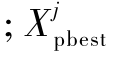是从种群的最优100p%，p∈(0，1］的个体中随机选择的个体；rand M(n)∈{1，2，…，n}是无重复随机选择的M维索引向量；r1和r2是［1，Np］中的随机数，且r1≠r2≠i；Fi是控制变异幅度的参数，服从历史最优自适应更新策略［15］:设定一个大小为H的集合MF来存储Fi的值，其初始值被设定为0.5.在每一次迭代中
其中，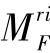
是随机从 MF中选取的 ri∈［1，H］；randc(μ，σ2)是服从均值为 μ，方差为 σ2的柯西分布的随机数.在每一代，如果采用当前的Fi生成的子代个体的适应度值优于父代，则该Fi被存储在集合SF中，在每一次迭代结束，即所有个体更新完成后，按式 (6)逐次循环更新MF中的值
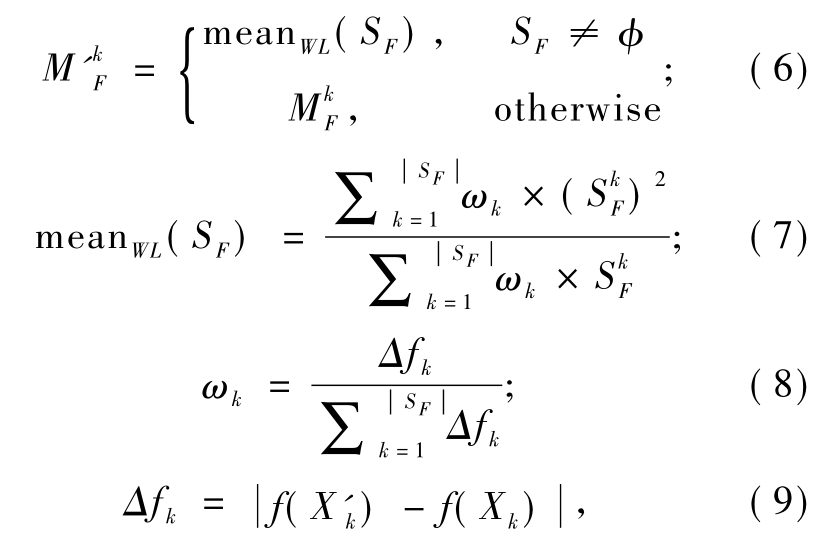
其中，k∈［1，H］初始值为1，然后递增并循环在［1，H］中取值.如果在本代中没有产生更优的子代，即 SF= φ，则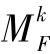 
不更新.
(3)选择:选择子代中最优的个体取代父代个体.
2.3 算法流程
综合以上基因重组策略和成功历史自适应克隆选择算法，笔者提出了新的克隆选择优化算法，该算法的步骤描述如下.
Step 1 初始化:随机产生规模为Np的抗体种群{X1，X2，…，XNp}.
Step 2 评价每一个个体的适应度值.
Step 3 基因重组:对每一个抗体Xi，实施基因重组，若产生的子代个体比当前抗体优，则取代当前抗体Xi，否则不更新 Xi，较差子代存入集合Archive.
Step 4 成功历史自适应克隆选择:对每一个抗体Xi进行克隆，成功历史自适应超变异和选择操作进行更新.
Step 5 判断是否满足终止条件，若满足，则输出最优值并结束，否则退回Step 3.
3 算法仿真分析
采用25个测试函数［16］进行试验仿真，对所提算法进行分析比较.这些测试函数涵盖了5个单峰和20个多峰函数，并进行了旋转、平移和复合等操作，决策变量维数从10维到50维，为问题的求解提出了很大的挑战.
3.1 参数设定
算法中所涉及的参数设定如下:种群个体数Np为10×D，其中D是问题的维度，基因重组率为0.7，克隆个体数Nc为1，变异中的衰变常数ρ设置为5，优秀个体的百分比p为0.2.
测试函数的最大评估次数mFES设置为10 000×D.为了确保对比公平，文中涉及的试验除特别说明外，选取的参数都是相同的，结果引用自算法提出的原文献.
3.2 基因重组和变异的策略对比分析
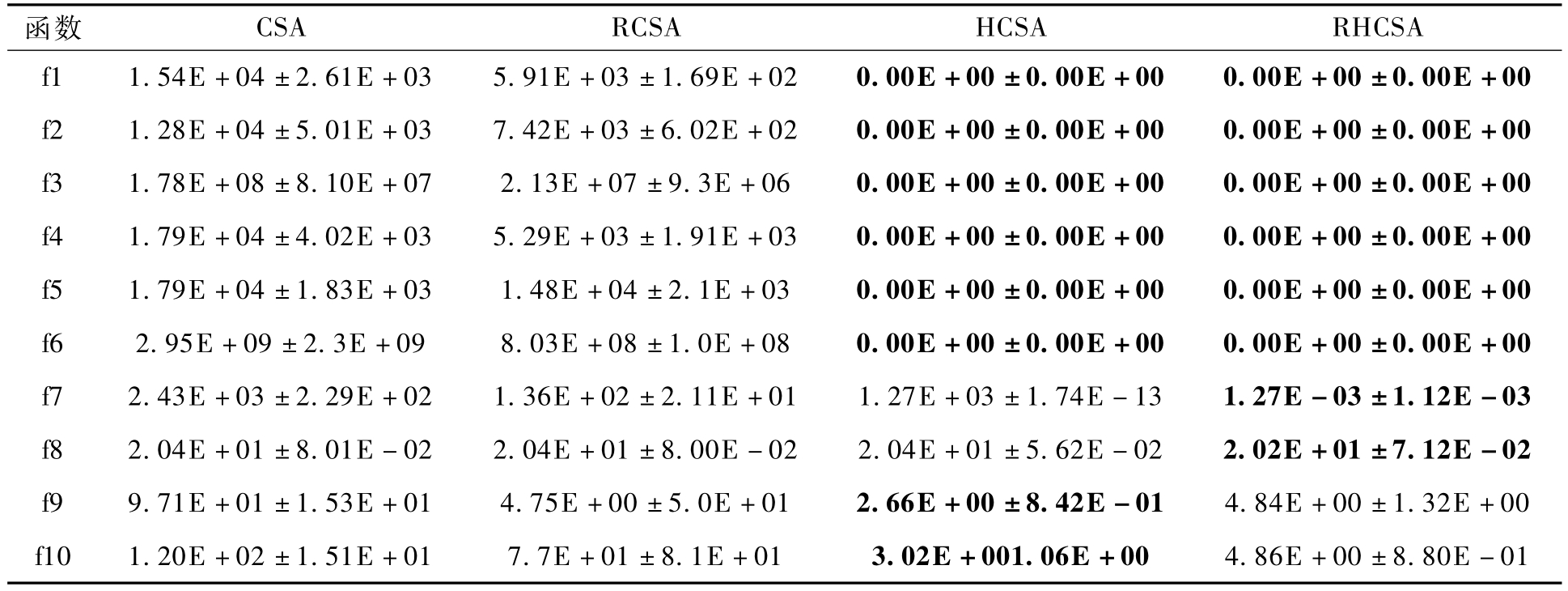
算法一共引入了两种策略，分别是基因重组和成功历史自适应克隆选择，为了验证这两种策略的有效性，下面在10维的测试函数上进行了仿真试验，并对其结果进行了对比.首先为了避免其它操作对算法的影响，选择只有克隆、超变异和选择3种基本操作的克隆选择算法(记为CSA)，在CSA上分别添加基因重组策略(记为RCSA)和成功历史自适应克隆选择策略(记为HCSA)，最后合并基因重组策略和成功历史自适应克隆选择策略(记为RHCSA).在CSA和RCSA中采用的是高斯变异的随机数进行超变异，其余的参数保持一致.实验结果如表1所示，受篇幅限制，截取了前10个函数的误差(均值±方差)的对比结果.从表1中可以看出基本的克隆、超变异和选择的操作在函数求解时表现较差，通过加入基因重组，一定程度上提升了算法的搜索能力，在除f5和f8以外的函数上都使误差减少了一个数量级.基因重组主要的功能是提高种群的多样性，避免陷入局部最优，但仅依靠基因重组策略算法的局部搜索能力还差强人意.成功历史自适应克隆选择策略可以大大提升算法的搜索能力，其搜索结果在f1～f6上都找到了最优值，除f7和 f8外都达到了很好的效果，甚至比两种策略相结合的效果还要好，但是在f7陷入了局部最优值，搜索结果比较差.两种策略相结合后的RHCSA在函数f1～f6上都定位到了全局最优值；虽然在函数 f9～f10上稍差，但基本可以接受；而在f7上的结果也比较让人满意.经过对比分析可以看出，基因重组策略和成功历史自适应克隆选择策略的引入能够有效提升算法的寻优能力和提升算法的稳定性.
3.3 与其他先进算法的对比分析
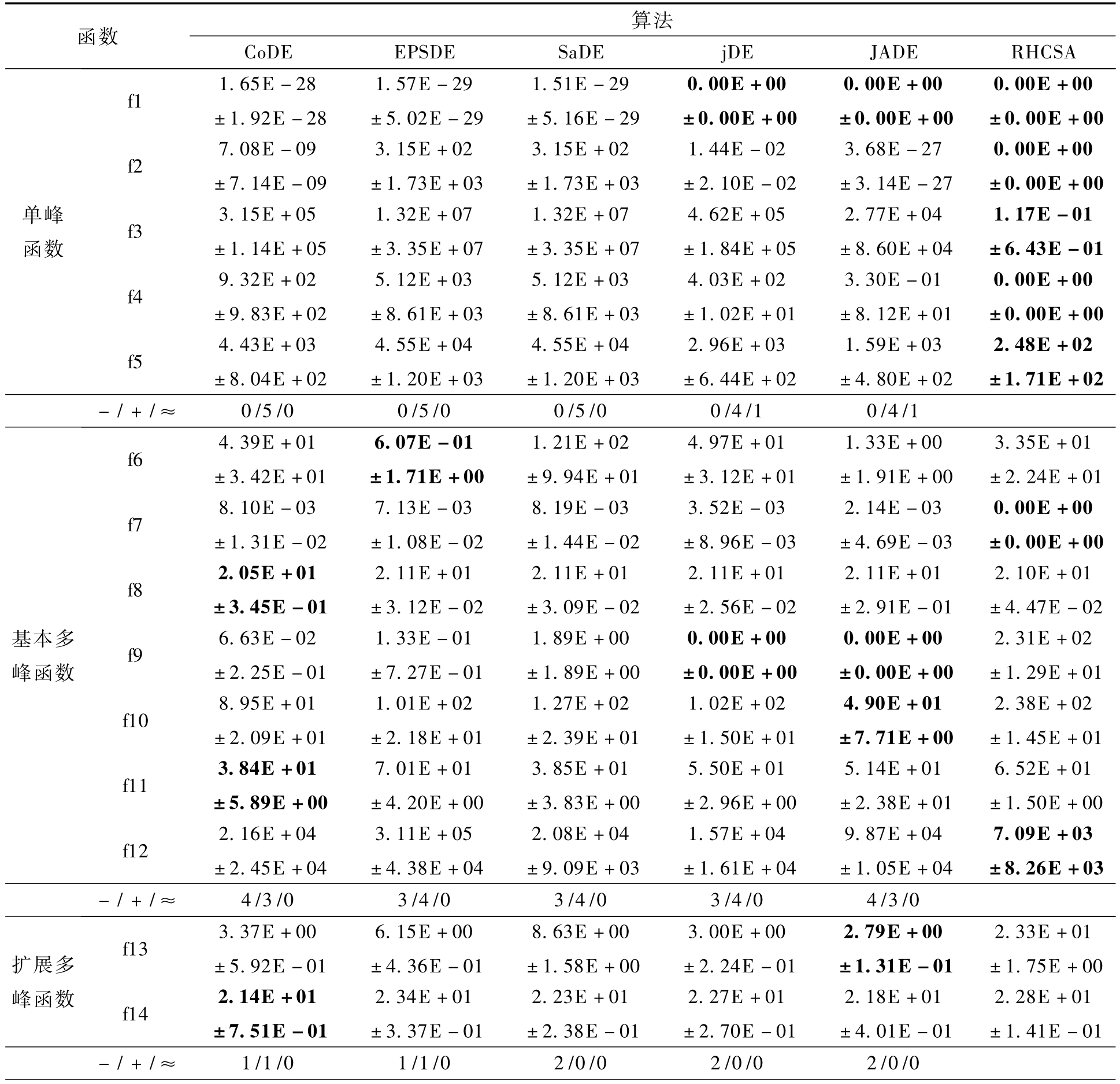
为了进一步测试所提算法的性能，将算法应用在25个测试函数在50维时进行仿真试验，并与 其 他 先 进 的 算 法 (CoDE［17］、EPSDE［18］、SaDE［19］、jDE［20］、JADE［21］) 进行对比分析，其误差结果(均值±方差)如表2所示.25个测试函数中前5个是单峰函数，笔者提出的算法在函数f1、f2、f4上均找到了全局最优值，在 f3和 f5上未能成功寻找到全局最优值，但比其他5个算法的效果好.可见所提算法RHCSA在单峰函数的寻优效果是值得肯定的.
f6～f12是基本多峰函数，主要考察算法在面对多峰函数时跳出局部最优的能力.RHCSA在f7找到了全局最优值.在 f6、f9和 f10上表现不够让人满意，在其余的函数上表现与其他算法相当.可以看出，在问题维度较高且存在多个局部最优的情况下，对算法提出的挑战更大，算法在求解时极易陷入局部最优值，从而影响最后的寻优效果.总体来看，RHCSA在求解基本多峰函数时表现尚可.
f13和f14是扩展的多峰函数，RHCSA未能成功寻找到全局最优值，但对比其他算法，表现尚可.f15～f25是混合复合函数，将基础的单峰
和多峰函数经过各种变换复合构造而成，这些函数大多拥有大量的局部最优值，且各种特性不可分割，部分函数还引入了旋转、噪声等，并人工设置了一些极易陷入的局部最优，为算法的求解提出了极大的挑战.
表1 10维测试函数上基本CSA和添加了基因重组和变异的策略对比
Tab.1 Comparison of Basic CSA，CSA with recombination and RHCSA on 10D benchmark functions
函数0.00E+00 ±0.00E+00 0.00E+00 ±0.00E+00 f2 1.28E+04 ±5.01E+03 7.42E+03 ±6.02E+02 0.00E+00 ±0.00E+00 0.00E+00 ±0.00E+00 f3 1.78E+08 ±8.10E+07 2.13E+07 ±9.3E+06 0.00E+00 ±0.00E+00 0.00E+00 ±0.00E+00 f4 1.79E+04 ±4.02E+03 5.29E+03 ±1.91E+03 0.00E+00 ±0.00E+00 0.00E+00 ±0.00E+00 f5 1.79E+04 ±1.83E+03 1.48E+04 ±2.1E+03 0.00E+00 ±0.00E+00 0.00E+00 ±0.00E+00 f6 2.95E+09 ±2.3E+09 8.03E+08 ±1.0E+08 0.00E+00 ±0.00E+00 0.00E+00 ±0.00E+00 f7 2.43E+03±2.29E+02 1.36E+02 ±2.11E+01 1.27E+03 ±1.74E-13 1.27E-03 ±1.12E-03 f8 2.04E+01±8.01E-02 2.04E+01 ±8.00E-02 2.04E+01 ±5.62E-02 2.02E+01 ±7.12E-02 f9 9.71E+01±1.53E+01 4.75E+00 ±5.0E+01 2.66E+00 ±8.42E-01 4.84E+00 ±1.32E+00 f10 1.20E+02 ±1.51E+01 7.7E+01 ±8.1E+01 3.02E+001.06E+00 CSA RCSA HCSA RHCSA f1 1.54E+04±2.61E+03 5.91E+03±1.69E+02 4.86E+00±8.80E-01
表2 笔者所提算法与先进算法在求解25个测试函数在50维时的结果对比
Tab.2 Comparison of RHCSA with other algorithms on 25 benchmark functions with 50D
函数 算法CoDE EPSDE SaDE jDE JADE RHCSA f1 1.65E-28±1.92E-28±0.00E+00 f2 7.08E-09±7.14E-09 1.57E-29±5.02E-29 1.51E-29±5.16E-29 0.00E+00±0.00E+00 0.00E+00±0.00E+00 0.00E+00 0.00E+00±0.00E+00 f3 3.15E+05±1.14E+05 3.15E+02±1.73E+03 3.15E+02±1.73E+03 1.44E-02±2.10E-02 3.68E-27±3.14E-27单峰函数1.17E-01±6.43E-01 f4 9.32E+02±9.83E+02 1.32E+07±3.35E+07 1.32E+07±3.35E+07 4.62E+05±1.84E+05 2.77E+04±8.60E+04 5.12E+03±8.61E+03 5.12E+03±8.61E+03 4.03E+02±1.02E+01 3.30E-01±8.12E+01 2.48E+02±1.71E+02-/+/≈0.00E+00±0.00E+00 f5 4.43E+03±8.04E+02 4.55E+04±1.20E+03 4.55E+04±1.20E+03 2.96E+03±6.44E+02 1.59E+03±4.80E+02 0/5/0 0/5/0 0/5/0 0/4/1 0/4/1 f6 4.39E+01±3.42E+01±2.24E+01 f7 8.10E-03±1.31E-02 6.07E-01±1.71E+00 1.21E+02±9.94E+01 4.97E+01±3.12E+01 1.33E+00±1.91E+00 3.35E+01 0.00E+00±0.00E+00 f8 2.05E+01±3.45E-01 7.13E-03±1.08E-02 8.19E-03±1.44E-02 3.52E-03±8.96E-03 2.14E-03±4.69E-03 2.31E+02±1.29E+01 f10 8.95E+01±2.09E+01 2.11E+01±3.09E-02 2.11E+01±3.12E-02 2.11E+01±2.56E-02 2.11E+01±2.91E-01基本多峰函数2.10E+01±4.47E-02 f9 6.63E-02±2.25E-01 1.33E-01±7.27E-01 1.89E+00±1.89E+00 0.00E+00±0.00E+00 0.00E+00±0.00E+00 2.38E+02±1.45E+01 f11 3.84E+01±5.89E+00 1.01E+02±2.18E+01 1.27E+02±2.39E+01 1.02E+02±1.50E+01 4.90E+01±7.71E+00 7.01E+01±4.20E+00 3.85E+01±3.83E+00 5.50E+01±2.96E+00 5.14E+01±2.38E+01 7.09E+03±8.26E+03-/+/≈6.52E+01±1.50E+00 f12 2.16E+04±2.45E+04 3.11E+05±4.38E+04 2.08E+04±9.09E+03 1.57E+04±1.61E+04 9.87E+04±1.05E+04 4/3/0 3/4/0 3/4/0 3/4/0 4/3/0 2.33E+01扩展多峰函数f13 3.37E+00±5.92E-01 6.15E+00±4.36E-01 8.63E+00±1.58E+00 3.00E+00±2.24E-01 2.79E+00±1.31E-01 2.28E+01±1.41E-01-/+/≈±1.75E+00 f14 2.14E+01±7.51E-01 2.34E+01±3.37E-01 2.23E+01±2.38E-01 2.27E+01±2.70E-01 2.18E+01±4.01E-01 1/1/0 1/1/0 2/0/0 2/0/0 2/0/0
RHCSA在混合复合函数上均未能找到全局最优值，但是其在 f18～f20、f22和 f25上的表现是算法中最好的，在 f15、f16和 f17上表现稍差，其余函数上的表现与其他算法不相上下.总体看来，新提出的 RHCSA在混合复合函数上的表现还是比较突出的.
从25个测试函数的整体比较来看，RHCSA在单峰函数上的处理效果较好，多峰函数上的求解能力一般，对于更复杂的混合复合函数的表现较突出，所以笔者提出的 RHCSA是非常有竞争力的.
续表2
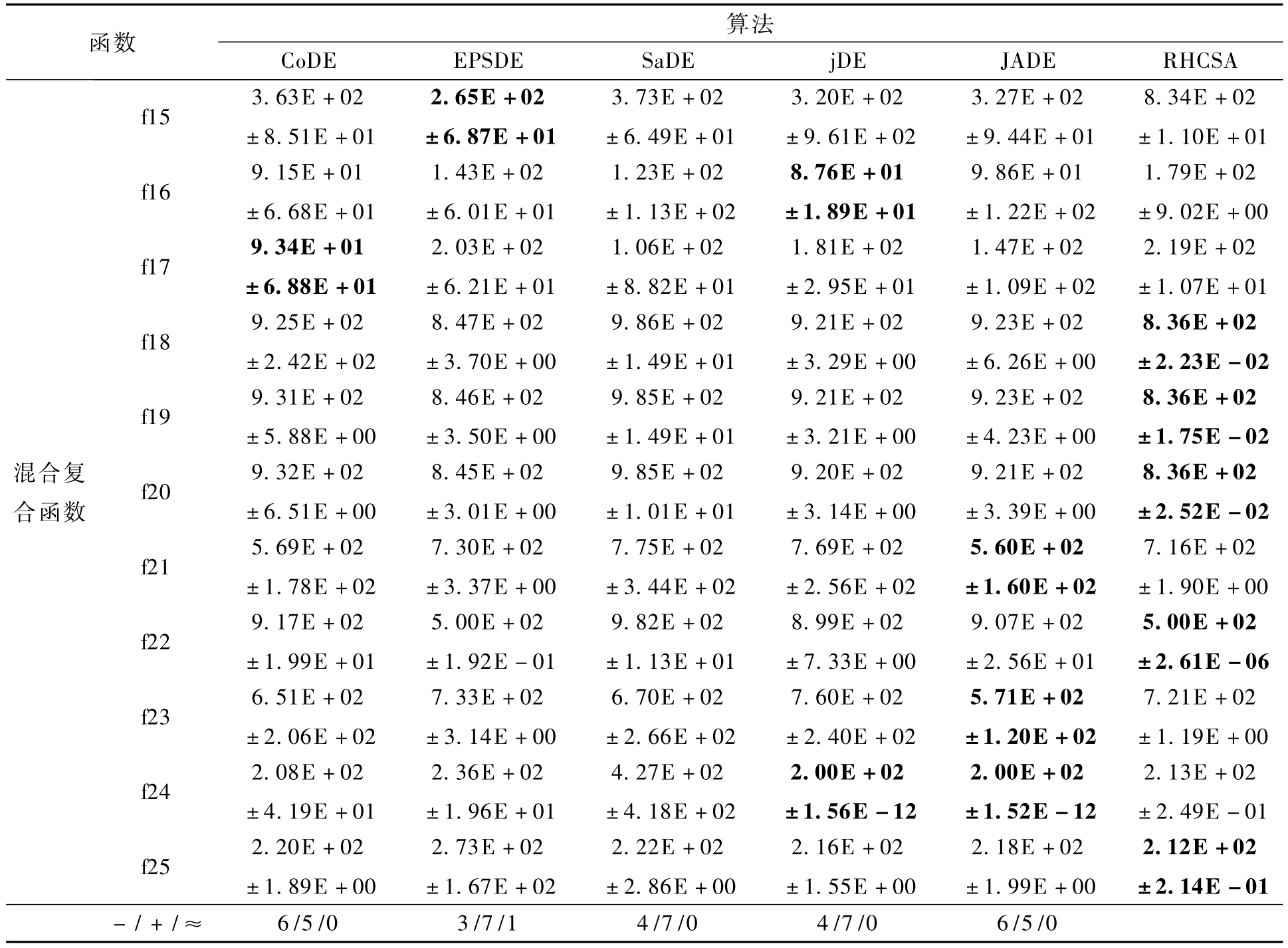
注:“-”、“+”、“≈”分别代表笔者提出的算法获得的结果“优于”，“差于”以及“等于”相比较的算法.
函数算法CoDE EPSDE SaDE jDE JADE RHCSA f15 3.63E+02±8.51E+01±1.10E+01 f16 9.15E+01±6.68E+01 2.65E+02±6.87E+01 3.73E+02±6.49E+01 3.20E+02±9.61E+02 3.27E+02±9.44E+01 8.34E+02 1.79E+02±9.02E+00 f17 9.34E+01±6.88E+01 1.43E+02±6.01E+01 1.23E+02±1.13E+02 8.76E+01±1.89E+01 9.86E+01±1.22E+02 2.19E+02±1.07E+01 f18 9.25E+02±2.42E+02 2.03E+02±6.21E+01 1.06E+02±8.82E+01 1.81E+02±2.95E+01 1.47E+02±1.09E+02 8.36E+02±2.23E-02 f19 9.31E+02±5.88E+00 8.47E+02±3.70E+00 9.86E+02±1.49E+01 9.21E+02±3.29E+00 9.23E+02±6.26E+00 8.36E+02±1.75E-02 f20 9.32E+02±6.51E+00 8.46E+02±3.50E+00 9.85E+02±1.49E+01 9.21E+02±3.21E+00 9.23E+02±4.23E+00混合复合函数8.36E+02±2.52E-02 f21 5.69E+02±1.78E+02 8.45E+02±3.01E+00 9.85E+02±1.01E+01 9.20E+02±3.14E+00 9.21E+02±3.39E+00 7.16E+02±1.90E+00 f22 9.17E+02±1.99E+01 7.30E+02±3.37E+00 7.75E+02±3.44E+02 7.69E+02±2.56E+02 5.60E+02±1.60E+02 5.00E+02±2.61E-06 f23 6.51E+02±2.06E+02 5.00E+02±1.92E-01 9.82E+02±1.13E+01 8.99E+02±7.33E+00 9.07E+02±2.56E+01 7.21E+02±1.19E+00 f24 2.08E+02±4.19E+01 7.33E+02±3.14E+00 6.70E+02±2.66E+02 7.60E+02±2.40E+02 5.71E+02±1.20E+02 2.12E+02 2.13E+02±2.49E-01 f25 2.20E+02±1.89E+00 2.36E+02±1.96E+01 4.27E+02±4.18E+02 2.00E+02±1.56E-12 2.00E+02±1.52E-12 2.73E+02±1.67E+02 2.22E+02±2.86E+00 2.16E+02±1.55E+00 2.18E+02±1.99E+00 6/5/0 3/7/1 4/7/0 4/7/0 6/5/0±2.14E-01-/+/≈
4 结论
针对传统克隆选择算法易早熟收敛和陷入局部最优的缺点，提出了基于成功历史自适应的混合克隆选择算法.该算法引入改进的基因重组策略来加强算法的全局搜索能力，并将成功历史自适应变异算子与超变异算子相结合提出了成功历史自适应超变异算子来提升算法的性能.仿真试验选取了25个包含单峰、多峰、混合复合的函数测试算法的性能，通过仿真结果可以看到，所提算法比传统的克隆选择算法具有更好的全局寻优和局部定位能力，与其他算法比较也显示了其竞争力.算法相关代码将整理发布在 https:∥github.com/haoyouqiezi/HCSA上.后续将继续深入研究免疫系统的原理和功能，提取和改进免疫算子，提高算法在处理优化问题上的性能.
［1］YANG X S，HE X.Nature-inspired optimization algorithms in engineering: overview and applications［M］.Nature-inspired computation in engineering.Springer international publishing，2016.
［2］肖俊明，周谦，瞿博阳，等.多目标进化算法及其在电力环境经济调度中的应用综述［J］.郑州大学学报(工学版)，2016，37(2):1-9.
［3］VLADICESCU F P，ALBEANU G.Recent advances in artificial immune systems［M］.Recent develop-ments in intelligent nature-inspired computing，2017.
［4］KHILWANI N，PRAKASH A，SHANKAR R，et al.Fast clonal algorithm ［J］.Engineering applications of artificial intelligence，2008，21(1):106-128.
［5］JIAO L C，LI Y，GONG M G，et al.Quantum-inspired immune clonal algorithm for global optimization ［J］.IEEE transactions on systems man＆cybernetics part b cybernetics a publication of the IEEE systems man＆cybernetics society，2008，38(5):1234-1253.
［6］GONG M G，JIAO L C，YANG J，et al.Lamarckian learning in clonal selection algorithm for numerical optimization ［J］.International journal of artificial intelligence tools，2010，19(1):19-37.
［7］MEGALA T，KASHYAP M，VIVEKANANDAN K.Clonal selection algorithm with adaptive lévy mutation operator［C］∥International conference on informatics and analytics.ACM，2016:127.
［8］LI R，ZHAN W，HAO Z.Artificial immune particle swarm optimization algorithm based on clonal selection［J］.Boletin tecnico/technical bulletin，2017，55(1):158-164.
［9］余航，焦李成，公茂果，等.基于正交试验设计的克隆选择函数优化［J］.软件学报，2010，21(5):950-967.
［10］宋丹，樊晓平，文中华，等.模糊非基因信息记忆的双克隆选择算法［J］.电子与信息学报，2017，39(2):255-262.
［11］谢新林，续欣莹，谢珺，等.一种基于粗糙集核值的克隆选择算法［J］.小型微型计算机系统，2016，37(5):992-996.
［12］BURNET M.The clonal selection theory of acquired immunity［M］.New York:Cambridge University Press，1959.
［13］DE CASTRO L N，VON ZUBEN F J.Learning and optimization using the clonal selection principle［J］.IEEE transactions on evolutionary computation，2002，6(3):239-251.
［14］张伟伟，林静静，景红蕾，等.基于基因重组的新颖克隆选择算法［J］.南京大学学报(自然科学版)，2016，52(4):647-655.
［15］TANABE R，FUKUNAGA A.Success-history based parameter adaptation for differential evolution［C］∥Evolutionary Computation.IEEE，2013:71-78.
［16］SUGANTHAN P N，HANSEN N，LIANG J J，et al.Problem definitionsand evaluation criteriaforthe CEC2005 special session on real-parameter optimization.
［17］WANG Y，CAI Z，ZHANG Q.Differential evolution with composite trial vector generation strategies and control parameters ［J］.IEEE transactions on evolutionary computation，2011，15(1):55-66.
［18］MALLIPEDDI R，SUGANTHAN P N，PAN Q K，et al.Differential evolution algorithm with ensemble of parameters and mutation strategies ［J］.Applied soft computing，2011，11(2):1679-1696.
［19］QIN A K，HUANG V L，SUGANTHAN P N.Differential evolution algorithm with strategy adaptation for global numerical optimization ［J］.IEEE transactions on evolutionary computation，2009，13(2):398-417.
［20］BREST J，GREINER S，BOSKOVIC B，et al.Self-adapting control parameters in differential evolution:a comparative study on numerical benchmark problems［J］.IEEE transactions on evolutionary computation，2006，10(6):646-657.
［21］ZHANG J，SANDERSON A C.JADE:adaptive differential evolution with optional external archive［J］.IEEE transactions on evolutionary computation，2009，13(5):945-958.