0 引言
焊接为各工业领域广泛使用的构件连接方式，由于焊接过程需使填充材料熔化使基材承受严重的热负荷，导致焊缝周围材料出现局部不均匀的微结构，形成不同的机械性能，使焊缝处出现应力集中及残余拉应力，故焊缝处的疲劳强度通常较母材低[1-4].焊缝疲劳寿命预测为当前疲劳领域研究热点,Motarjemi和Lotsberg等[5-6]通过对不同类型的焊接接头进行正弦载荷疲劳试验，证实焊缝穿透尺寸与焊喉裂纹扩展速率成正比.阳清泉、惠延波等[7-8]利用fatigue软件自带的刚/柔焊缝S-N曲线对车架焊缝进行疲劳评估. Bertini等[9]基于名义应力法，研究单一角焊缝在扭转载荷作用下的抗疲劳性能.郭政和邹艳妮等[10-11]用等效结构应力法，分析单一对接接头在正弦波形加载条件下焊缝的疲劳寿命.赵磊等[12]分析了不同吊装工况下吊具的T型焊缝熔透深度对结构疲劳寿命的影响.Rao和Zhou等[13-14]采用等效结构应力法和IIW焊接疲劳评估标准对铝合金车身在不同工况下的疲劳寿命进行预测.
现有学者大多针对简单焊接试样通过试验或数值仿真方法对焊接疲劳性能进行评估[15-18]，而针对复杂工程结构的焊缝疲劳寿命的试验及仿真分析较少.笔者以动车水箱为研究对象，该水箱结构由上盖板、内胆下体、内部防波板、吊耳、扣筋及加强筋板等构件焊接而成，在强化台架振动试验中,其高应力区焊缝极易发生断裂失效，故针对该结构焊缝开展疲劳寿命仿真及试验研究十分必要，可为类似焊接结构的疲劳设计提供有效分析算法.
1 焊缝疲劳分析理论
1.1 试验原材料
目前针对焊缝疲劳评估标准主要有：①英国钢铁结构疲劳评估标准(BS7608)；②日本标准(JISE4207)；③国际焊接学会标准(IWW2003)等.其中BS7608标准适用于评估屈服强度小于700 MPa的焊接钢结构，根据焊接接头形式、局部应力集中、不连续尺寸、加工要求、潜在裂纹位置、应力方向和残余应力等影响因素，将焊缝分为B、C、S、D、E、F、F2、G、W 9个等级，文献[19]中给出了相应9个焊缝等级的试验S-N曲线，如图1所示.
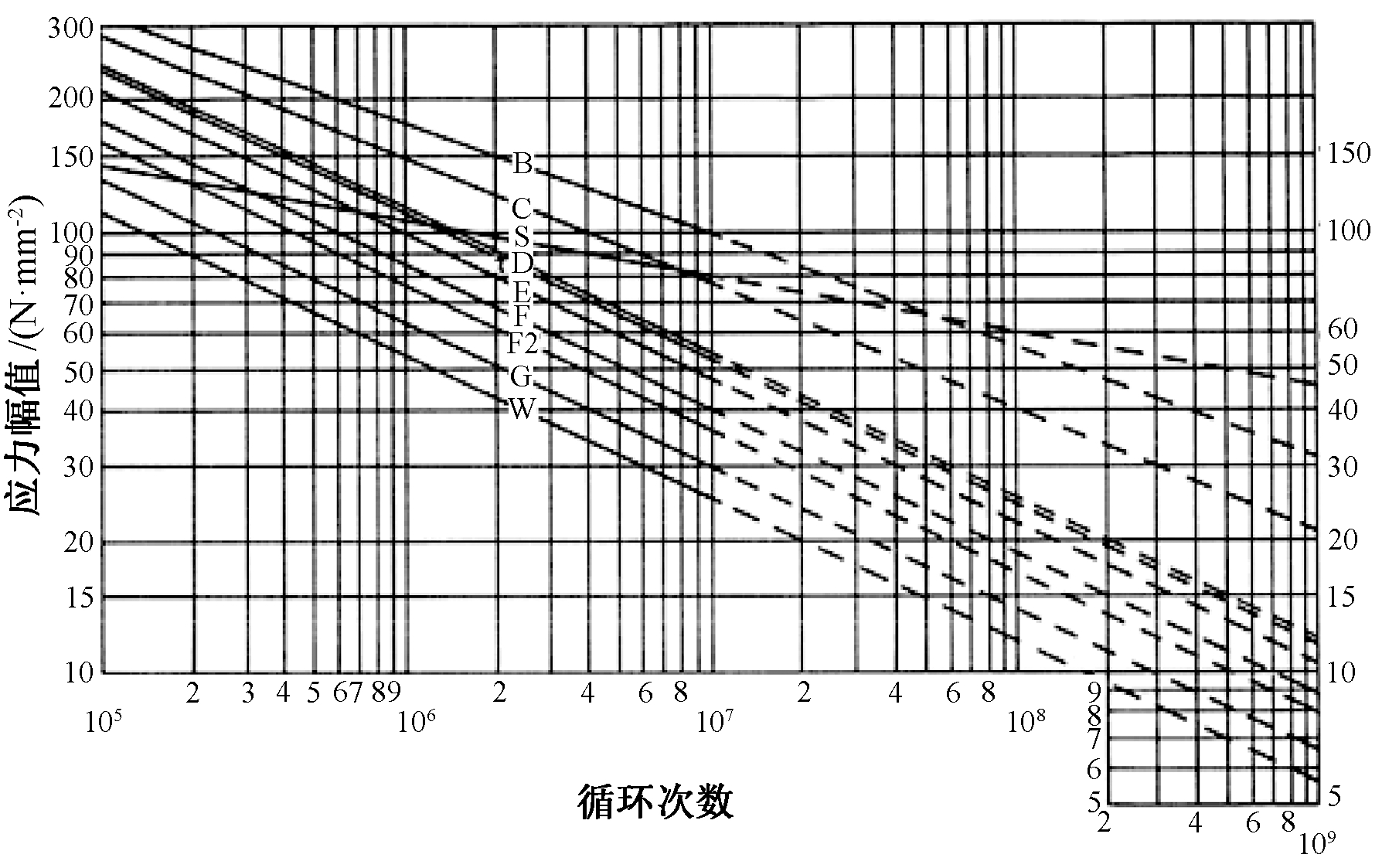
图1 不同等级焊缝试验S-N曲线
Fig.1 Different grades of weld test S-N curve
BS7608标准中各级焊缝S-N曲线方程为：
lg N=lg C0-dσ-mlg Sr,
(1)
式中：N为焊缝达到疲劳失效的循环次数；C0为焊缝S-N曲线的相关常数；d为应力低于平均值的标准偏差；σ为焊缝S-N曲线的标准偏差；m为焊缝S-N曲线的反向斜率；Sr为焊缝应力变化范围.
式(1)适用于各类钢结构，不同等级焊缝所对应的焊缝参数如表1所示.该水箱焊缝主要包括搭接焊缝、角焊缝和T型焊缝，其焊缝类型分别属于B级、F级和W级，计算时可选用相应的焊缝S-N曲线.
根据焊缝类型和应力水平Sri，由图1中的S-N曲线可得相应的疲劳循环次数Ni：
(2)
(3)
式中：Cd1、Cd2分别为图1中107(拐点)循环次数之前和之后曲线所对应的常数；Ni为焊缝疲劳失效循环次数.
当焊缝应力发生变化时，可通过雨流计数计算各级应力对应的疲劳循环次数，根据Miner线性累积损伤理论，认为该焊缝在各级应力作用下的疲劳损伤是独立的，其总疲劳损伤可线性累加，即：
(4)
式中：ni为对应当前载荷水平的疲劳寿命；Ni为焊缝疲劳失效循环次数.
当
时，认为该焊缝疲劳失效.在随机载荷作用下，采用线性累积理论可得到焊缝疲劳寿命为：
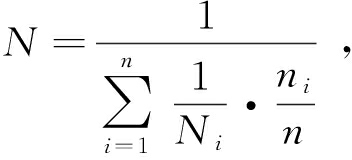
(5)
式中:
为一个采样时长范围内应力值为Sri出现次数占总次数的百分比；Ni为对应Sri的疲劳失效循环次数.
表1 不同等级焊缝S-N曲线参数
Tab.1 S-N curve parameters for different grades of welds
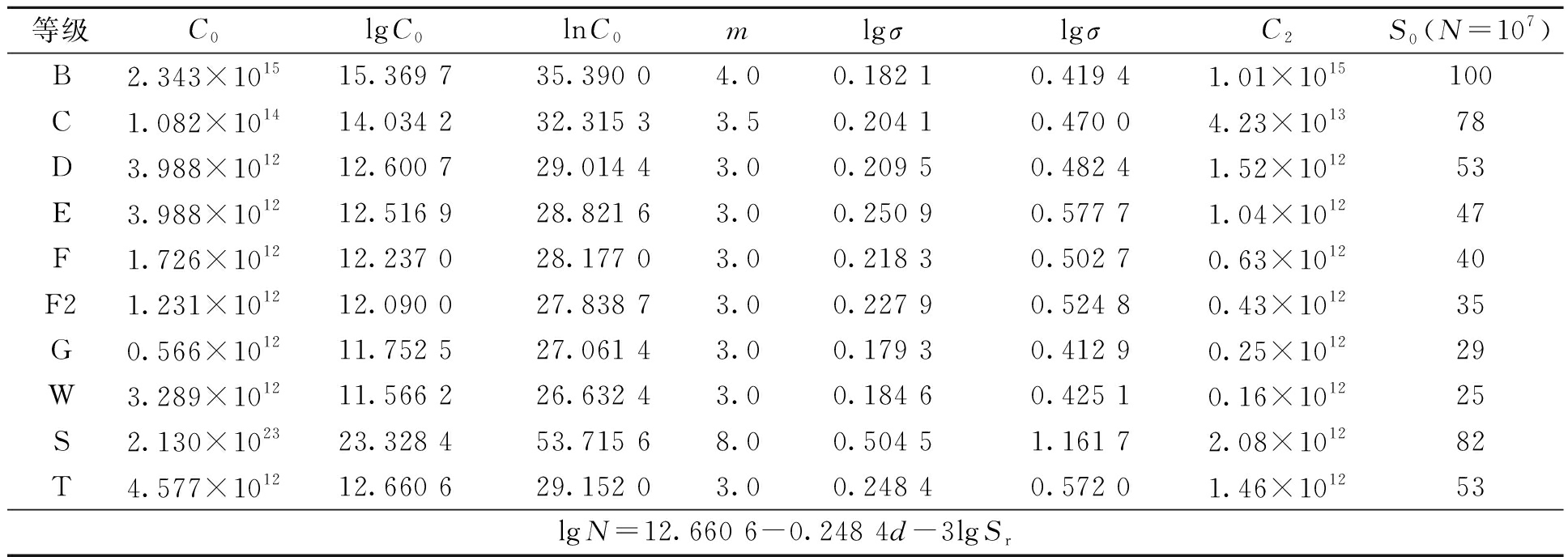
等级C0lgC0lnC0mlgσlgσC2S0(N=107)B2.343×101515.369 735.390 04.00.182 10.419 41.01×1015100C1.082×101414.034 232.315 33.50.204 10.470 04.23×101378D3.988×101212.600 729.014 43.00.209 50.482 41.52×101253E3.988×101212.516 928.821 63.00.250 90.577 71.04×101247F1.726×101212.237 028.177 03.00.218 30.502 70.63×101240F21.231×101212.090 027.838 73.00.227 90.524 80.43×101235G0.566×101211.752 527.061 43.00.179 30.412 90.25×101229W3.289×101211.566 226.632 43.00.184 60.425 10.16×101225S2.130×102323.328 453.715 68.00.504 51.161 72.08×101282T4.577×101212.660 629.152 03.00.248 40.572 01.46×101253lgN=12.660 6-0.248 4d-3lgSr
2 水箱随机振动疲劳试验
动车组在行驶过程中，由于起制动及转向等加速度作用，其上的车载设备(如水箱等)将受到纵向、垂向及横向振动载荷，故要求对车载设备进行随机振动台架试验，验证其结构及焊缝设计及制造质量是否满足使用要求.根据GB/T 21563—2008《轨道交通机车车辆设备冲击和振动试验标准》，为缩短试验时间，要求车载设备在增强振动载荷作用下，保持5 h完好无损，以等效该设备在实际载荷作用下正常工作25 a.本试验采用MPA3436/h1 859 A电动振动台架，频率范围为5～2 000 Hz，将水箱4个吊耳固定在试验台上，并在该处施加振动激励，在水箱的两侧面的中心位置分别安装两个加速度传感器以拾取振动响应信号，水箱现场安装如图2所示.
图2 水箱安装图
Fig.2 Tank installation diagram
根据GB/T 21563—2008，在试验中输入随机振动激励曲线，如图3所示，该曲线属于频域振动信号.根据水箱质量及GB/T 21563—2008中的相关公式可确定随机振动试验的激励频率范围：f1为2.5 Hz，f2为75 Hz，并能确定图3中ASD标称曲线数: ASD2.5为0.260 (m/s2)2/Hz，ASD5和ASD20均为2.068 (m/s2)2/Hz，ASD75为0.148 (m/s2)2/Hz.图4为图3频域随机振动激励曲线对应的时域加速度信号，表示每一时刻对应一个加速度幅值，由于随机振动疲劳数值模拟只能载入时域载荷，该时域信号是后续数值模拟的重要激励曲线.
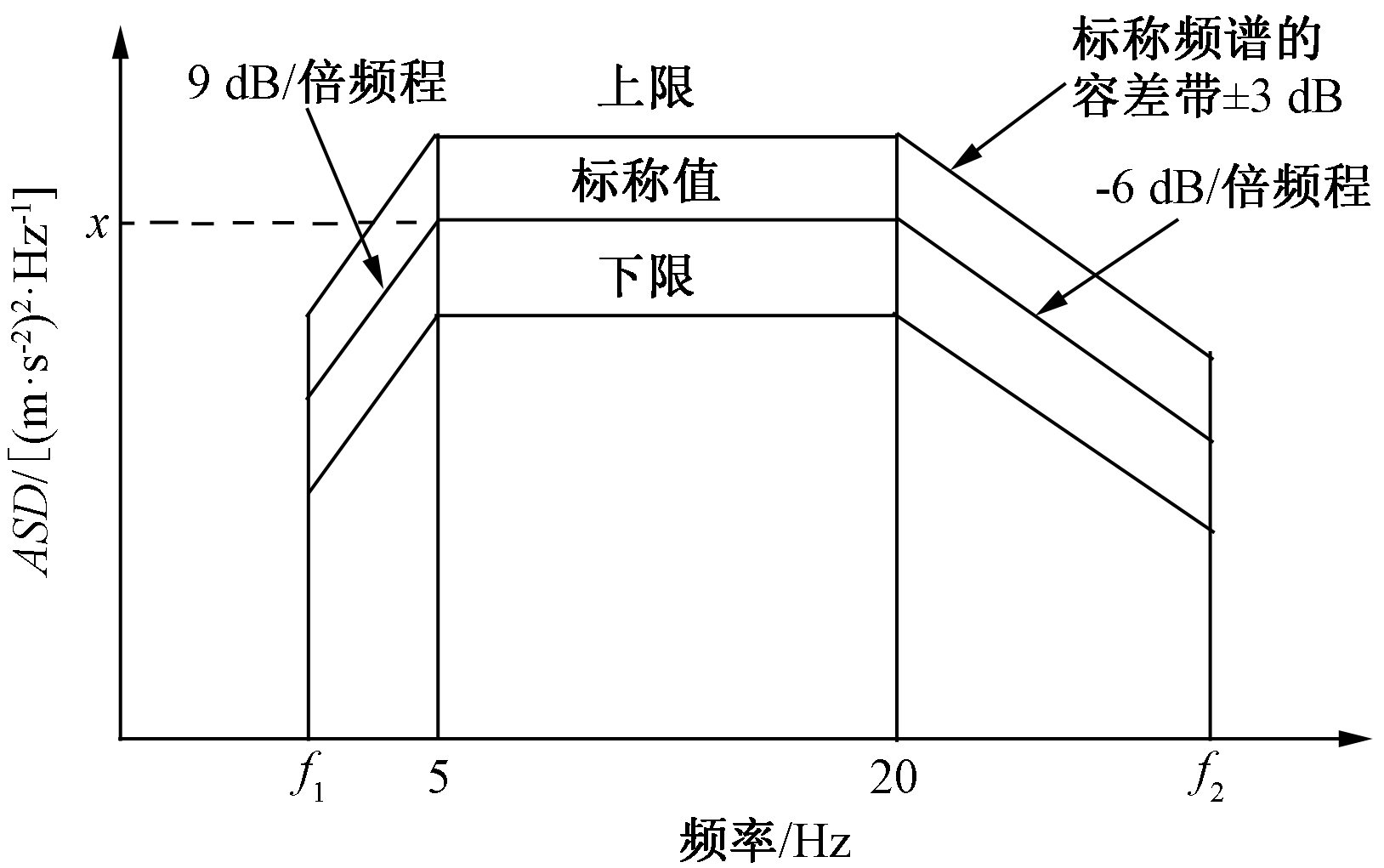
图3 I类A级车体激励功率谱
Fig.3 Class I and A vehicle motivation power spectrum
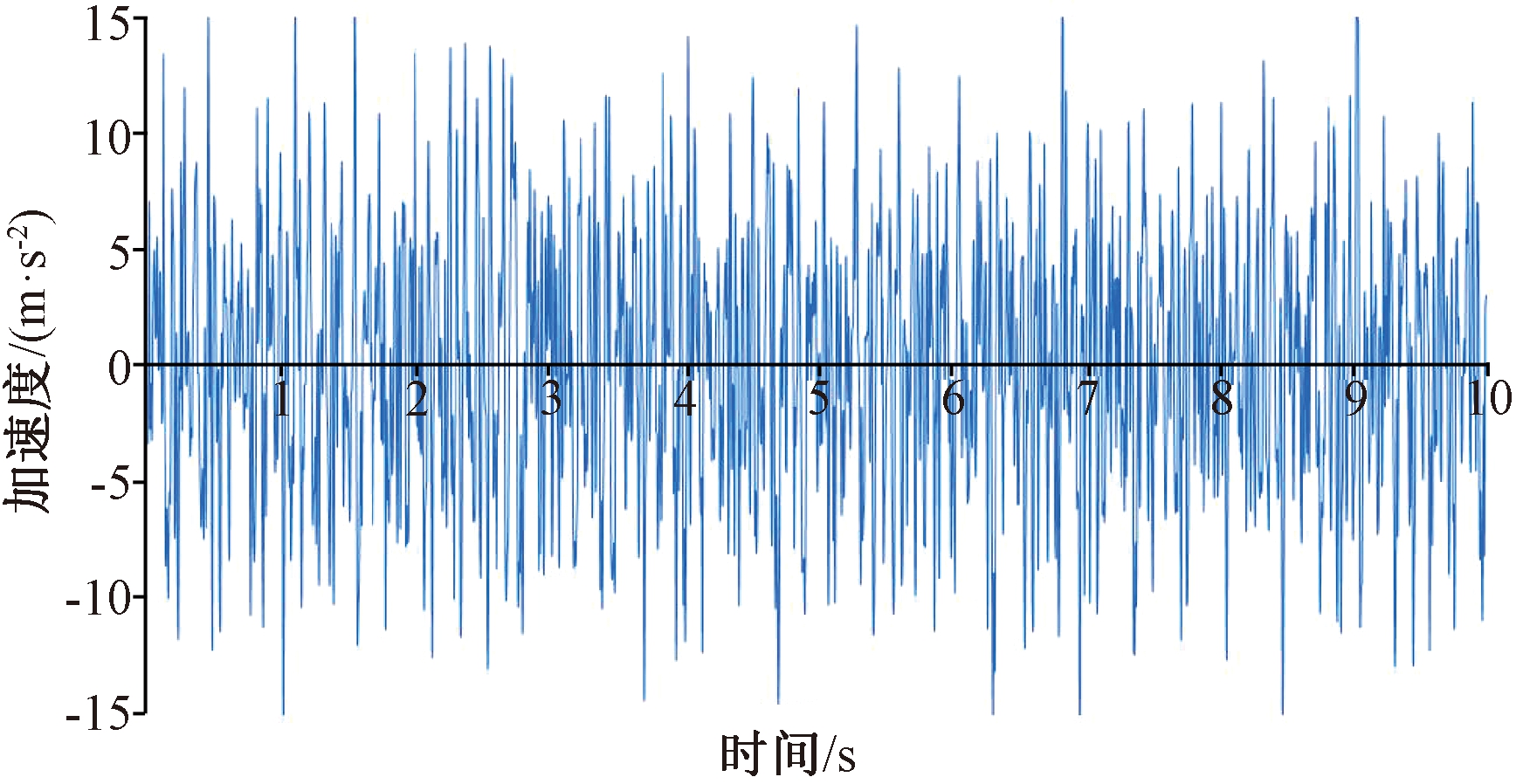
图4 激励加速度时域信号
Fig.4 Excitation acceleration time domain sign
图5为施加在吊耳处4个加速度激励信号的实测曲线图，从图5中可以看出，吊耳处实测的加速度激励与规范中标称激励曲线图3一致，其中红色箭头所指为标称值激励曲线.图6为固定在水箱两侧加速度传感器拾取的振动响应信号曲线，由图6可以看出，水箱振动响应加速度峰值对应的频率为20.625 Hz，其加速度功率谱密度峰值为259.59 (m/s2)2/Hz.
图5 激励加速度功率谱密度
Fig.5 Excitation acceleration power spectral density
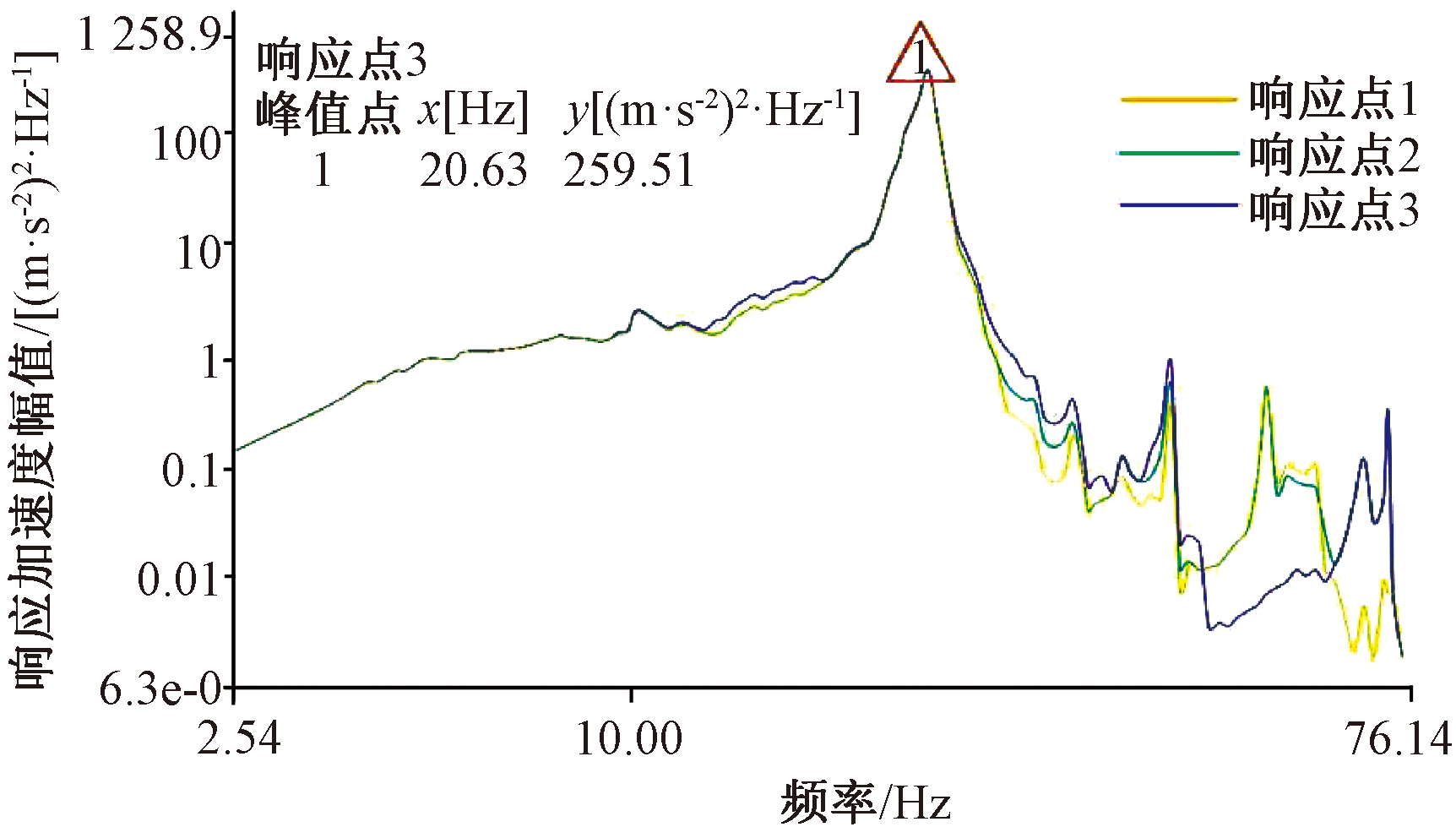
图6 响应加速度功率谱密度
Fig.6 Response acceleration power spectral density
图7 焊缝失效结果图
Fig.7 Weld failure results
该随机振动试验持续15 min后，水箱上盖板与内胆下体连接焊缝处出现裂纹，导致内部液体流出，如图7所示，说明此处焊缝疲劳寿命远未达到试验要求.以下将针对该试验工况，通过有限元建模，仿真分析该水箱母材及各焊缝的疲劳寿命，为设计能满足该振动台架试验要求的焊接水箱提供有效分析方法.
3 水箱焊缝疲劳数值模拟
3.1 有限元模型
该水箱是由不同厚度的不锈钢板材焊接而成，其中水接触部分为316 L不锈钢，其他部分为304不锈钢.利用HYPERMESH软件建立包括焊缝的水箱有限元模型，单元类型为四节点壳单元，将其内部的水处理为附加质量，分布在水箱内壁，单元尺寸为10 mm，单元总数为87 560，焊缝采用刚性壳单元，其厚度取
(t为母材厚度)，焊缝角度为45°，焊缝模型定义如图8所示，图中红色线为定义的焊缝单元，其他颜色表示水箱结构的板壳单元.施加垂向9.8 m/s2重力加速度模拟重力场.水箱4个吊耳底面为基础激励的输入部位，分别输入垂向基础激励加速度信号，如图4所示.
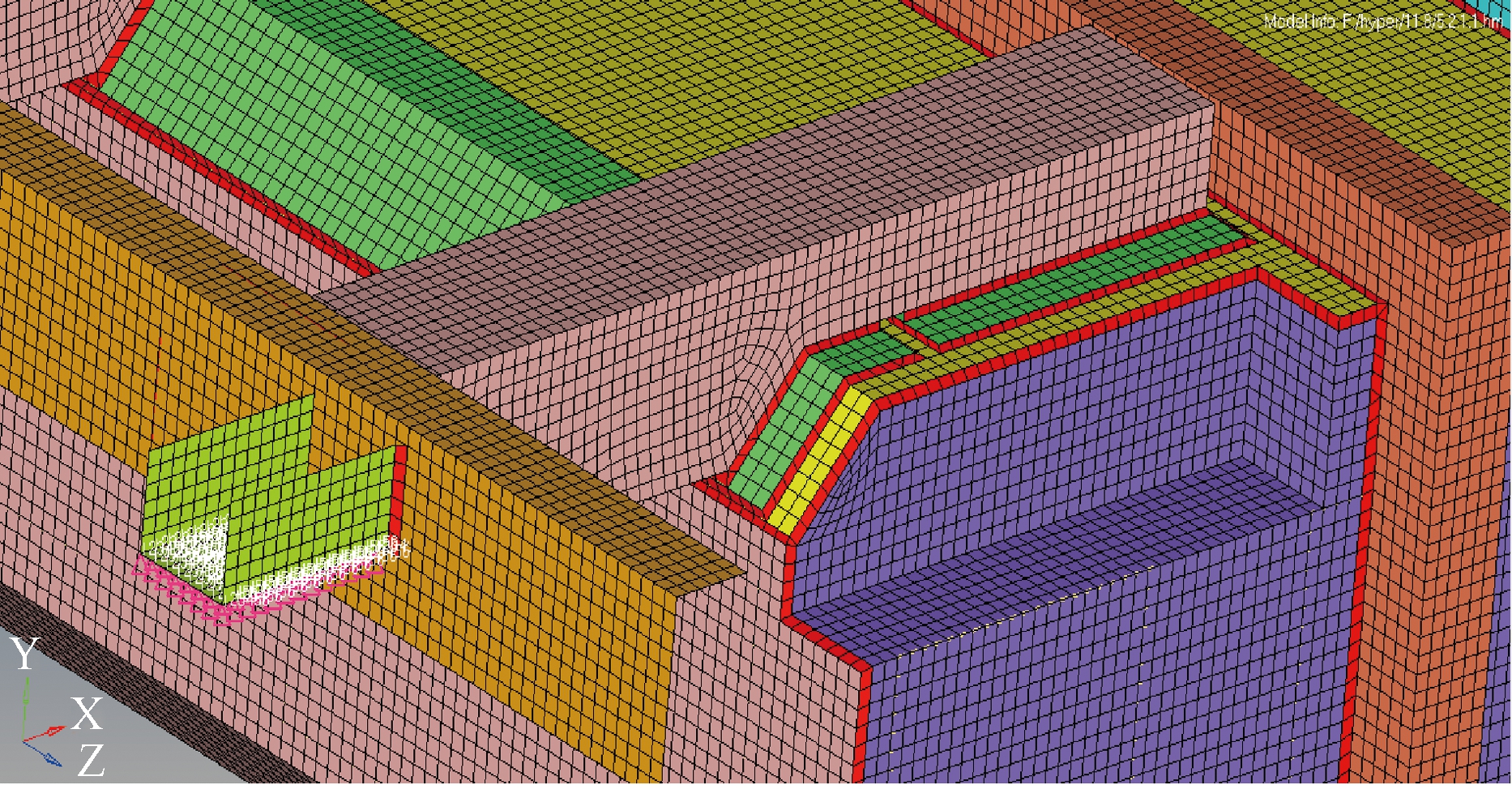
图8 焊缝有限元模型
Fig.8 Finite element model of weld
3.2 有限元模型
将HYPERMESH建立的有限元模型导入FATIGUE软件，使用全寿命疲劳分析模块对水箱及焊缝进行疲劳寿命计算.根据水箱母材及各焊缝类型设置相应的S-N曲线，该水箱焊缝包括角焊缝、搭接焊缝及T型焊缝，分别对应F级、B级、D级焊缝S-N曲线，设置goodman系数，计算水箱母材及焊缝疲劳寿命.
图9为水箱的等效应力图，从图9可以看出，水箱最大应力为103 MPa，位于水箱上盖板与内胆下体的焊缝连接处.图10为水箱母材及各焊缝的疲劳寿命分布图，图中青蓝色部分为水箱母材的疲劳寿命，其疲劳循环次数接近2×1022次，从图10可以看出,母材的疲劳寿命远远大于焊缝处的疲劳寿命.图11为该水箱所有焊缝的疲劳寿命分布图，其中上盖板与内胆下体焊缝连接处循环次数最低，发生在图9中最大等效应力处，其最低循环次数为 20 000次.由图6可知，水箱实测最大响应频率为20.625 Hz，该频率对应的振动周期为0.048 s，据此可得20 000次循环对应的焊缝疲劳寿命约为16 min，与试验结果基本吻合，由此验证该疲劳寿命分析方法及结果的正确性及有效性，说明该数值模型及分析方法可有效用于此类焊接结构的疲劳寿命分析及预测.
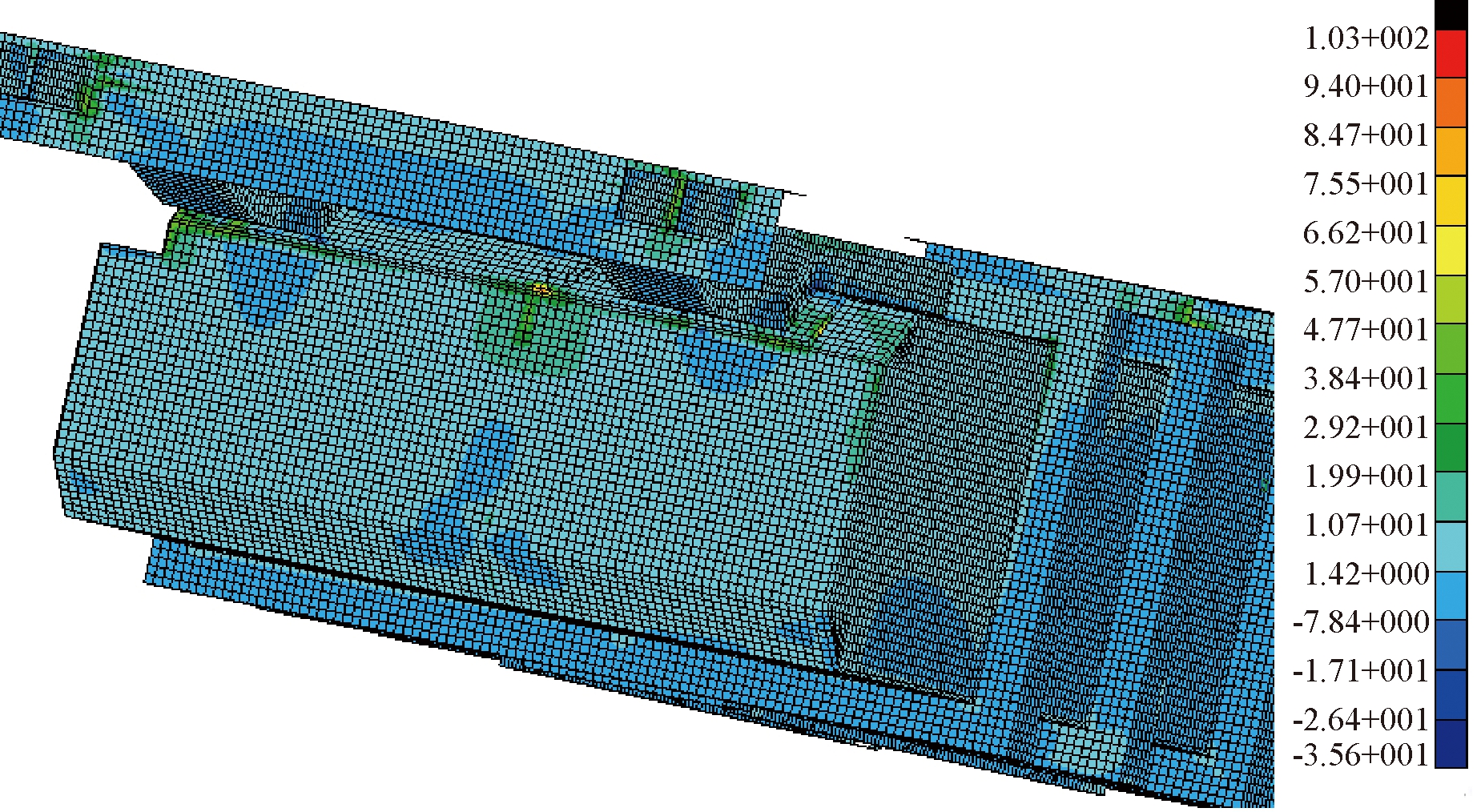
图9 结构等效应力分布图
Fig.9 Structural equivalent stress results
图10 结构疲劳寿命分布图
Fig.10 Structural fatigue life results
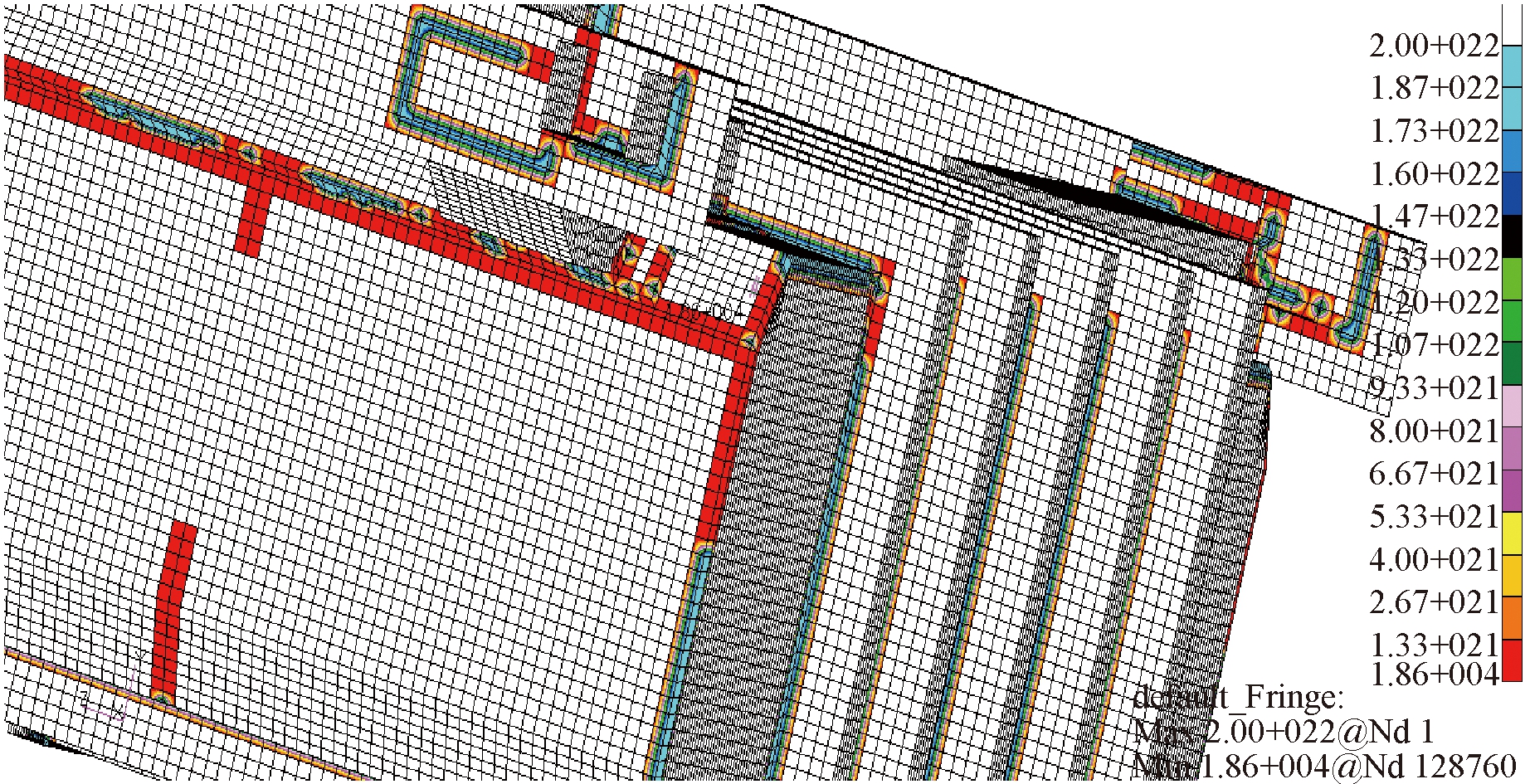
图11 低寿命焊缝分布图
Fig.11 Weld fatigue life results
4 结论
笔者以动车水箱实际焊接结构为研究对象，通过振动台架试验和有限元数值模型对其疲劳寿命进行试验和仿真研究.其中台架试验仅持续15 min，就发生上盖板与内胆下体处焊缝失效而漏水，说明该水箱疲劳寿命远未达到试验要求.为今后设计能满足该振动台架试验要求的焊接水箱提供有效分析方法，根据该台架试验工况建立焊接水箱疲劳寿命分析有限元模型，基于名义应力法针对不同类型的焊缝设置相应的S-N曲线，计算在随机振动载荷作用下，结构母材及焊缝的疲劳寿命，并与振动台架试验结果对比，两者的失效部位及疲劳寿命基本吻合，说明该数值模型及仿真算法合理有效.利用该方法可在前期设计中及时发现低寿命焊缝发生部位，预测其疲劳寿命，并可基于仿真结果，合理规划焊缝布局，优化焊接结构，使其能顺利通过类似的强化振动疲劳试验，为焊接结构的疲劳寿命设计提供有效分析方法.
[1] LEE C H, JANG G C, PARK H C, et al. Effect of vibration during welding on the fatigue strength of structural steel weldments[J]. Solid state phenomena, 2007, 124/125/126:1329-1332.
[2] ZHANG Y H, MADDOX S J. Investigation of fatigue damage to welded joints under variable amplitude loading spectra[J]. International journal of fatigue, 2009, 31(1):138-152.
[3] BRUDER T, STÖRZEL K, BAUMGARTNER J. Fatigue assessment of seam welds of automotive components by local stress approaches[J]. Materialwissenschaft and werkstofftechnik, 2010, 39(10):726-733.
[4] GAO Y H, ZHAO W Z. Adaptive optimization with weld fatigue constraints based on surrogate model for railway vehicles[J]. Mechanics based design of structures and machines, 2014, 42(2):244-254.
[5] MOTARJEMI A K, KOKABI A H, BURDEKIN F M. Comparison of fatigue life for T and cruciform welded joints with different combinations of geometrical parameters[J]. Engineering fracture mechanics, 2000, 67(4): 313-328.
[6] LOTSBERG I, W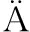
STBERG S, ULLE H, et al. Fatigue testing and S-N data for fatigue analysis of piles[J]. Journal of offshore mechanics and arctic engineering, 2010,132:041602-1.
[7] 阳清泉, 谷正气, 米承继,等. SF33900型矿用自卸车车架疲劳寿命分析[J]. 汽车工程, 2012, 34(11):1015-1019.
[8] 惠延波, 王宏晓, 冯兰芳,等. 基于MSC.fatigue的某轻型客车车架疲劳寿命分析[J]. 郑州大学学报(工学版), 2013, 34(1):87-90.
[9] BERTINI L, CERA A, FRENDO F. Experimental investigation of the fatigue resistance of pipe-to-plate welded connections under bending torsion and mixed mode loading[J]. International journal of fatigue, 2014, 68(9):178-185.
[10] 郭政, 王会利, 黄才良. 基于Fe-safe的K形对接焊缝疲劳分析[J]. 沈阳大学学报(自然科学版), 2013, 25(6):499-501.
[11] 邹艳妮, 李耀, 罗东. 等效结构应力法在高强钢疲劳寿命预测中的应用[J]. 机械科学与技术, 2015, 34(8):1298-1301.
[12] 赵磊, 张昭, 王松,等. 燃油箱吊座焊缝的强度和疲劳有限元分析[J]. 计算机辅助工程, 2015, 24(1):7-11.
[13] RAO K B, ANOOP M, RAGHAVA G, et al. Probabilistic fatigue life analysis of welded steel plate railway bridge girders using S-N curve approach[J]. Proceedings of the institution of mechanical engineers part journal of risk and reliability, 2013, 227(4):385-404.
[14] ZHOU X, CHEN B Z, LIU L. An assessment of two methods for fatigue life prediction of an aluminum alloy car body[C]∥International Conference on Transportation Engineering. Dailan: ICTE, 2015:2234-2242.
[15] GORASH Y, COMLEKCI T, MACKENZIE D. Comparative study of FE-models and material data for fatigue life assessments of welded thin-walled cross-beam connections [J]. Procedia engineering, 2015, 133:420-432.
[16] SAVAIDIS G, MALIKOUTSAKIS M. Advanced notch strain based calculation of S-N curves for welded components[J]. International journal of fatigue, 2016, 83:84-92.
[17] 苏有华. 基于主S-N曲线法的典型钢桥焊接节点疲劳寿命评估[D]. 兰州：兰州理工大学土木工程学院, 2014.
[18] 兆文忠, 魏鸿亮, 方吉,等. 基于主S-N曲线法的焊接结构虚拟疲劳试验理论与应用[J]. 焊接学报, 2014, 35(5):75-78.
[19] BS7608. Code of practice for fatigue design and assessment steel structures[S]．British Standards Institution，1993.