0 引言
我国现行国家规范规定的结构设计方法为半概率极限状态设计方法.半概率极限状态设计方法是基于极限状态函数(或称为功能函数)Z=R-S进行研究的[1]，其中，随机变量R和S分别代表抗力和(全部)荷载效应的极值.当考虑荷载的时变特性时，荷载效应极值S为结构随机动力响应的最大值，即
其中，Y(t)为结构的线性或非线性随机响应，T为结构振动分析所考虑的持时.
结构极值响应
估计的主要困难在于分布尾部的估计.Monte Carlo模拟方法适用于具有确定性解的任何结构,是进行结构极值响应估计最常用的方法[2].然而,为得到极值分布的尾部，Monte Carlo模拟方法的计算费用极其昂贵，不是一种最佳的方法.为了提高尾部估计的效率，人们提出了加速模拟方法.Naess等[3]基于结构随机响应平均穿越率函数的尾部行为，提出一种结构极值响应估计的加速模拟方法；Balesdent等[4]提出基于空间自协方差最佳插值法的加速模拟方法；Taflandis等[5]提出基于移动最小均方根响应面的加速模拟方法;Grigoriu等[6]假设结构极值响应服从广义极值分布，提出结构极值响应估计的加速模拟方法;He等[7]假设结构极值响应近似服从移位广义对数正态分布，提出结构极值响应估计的加速模拟方法.上述加速模拟方法中的后两种，在结构极值响应估计中，表现出良好的数值稳定性、计算效率和计算精度.
除了模拟方法，人们也提出了其他类型的结构极值响应估计方法.Michaelov等[8]假设结构极值响应分布等价于随机响应穿越事件的分布，提出非平稳高斯激励下线性结构极值响应的估计方法.He[9]利用结构响应穿越事件的Poisson分布假定，由Rice穿越率计算式和结构响应及其导数的联合分布，建立了结构非线性响应的极值估计方法.相对而言，这些非模拟方法的计算效率要低于加速模拟方法.
笔者的主要目的为对Grigoriu等提出的加速模拟方法和He等提出的加速模拟方法进行对比研究，对比分析这两种加速模拟方法的计算效率和计算精度，为进行结构极值响应估计提供算法选择方面的建议和参考.
1 加速模拟方法的一般流程
加速模拟方法的基本思想是预先假设结构极值响应服从某类分布，再通过建立基于样本的分布参数估计方法，然后利用随机模拟方法生成有限容量的响应样本，从而估计出分布参数及结构极值响应分布.与直接模拟方法相比，加速模拟方法需要更少的响应样本估计极值响应的分布尾部，从而提高了结构极值响应尾部估计的效率.另一方面，因为加速模拟方法在本质上仍然属于一种随机模拟方法，因此，该类方法也适用于任何具有确定性解的结构随机振动问题，具有广泛的工程适用性.
目前的加速模拟方法主要有两种：一种是Grigoriu等提出的基于广义极值分布假定的加速模拟方法;另一种是He等提出的基于移位广义对数正态分布的加速模拟方法.这两种算法具有相同的流程，如图1所示.这两种加速模拟方法的区别之处在于采用了不同的极值分布假设及其参数估计方法.关于GEV和SGLD的函数形式和参数估计方法，将分别在本文的第2小节和第3小节进行详细介绍.
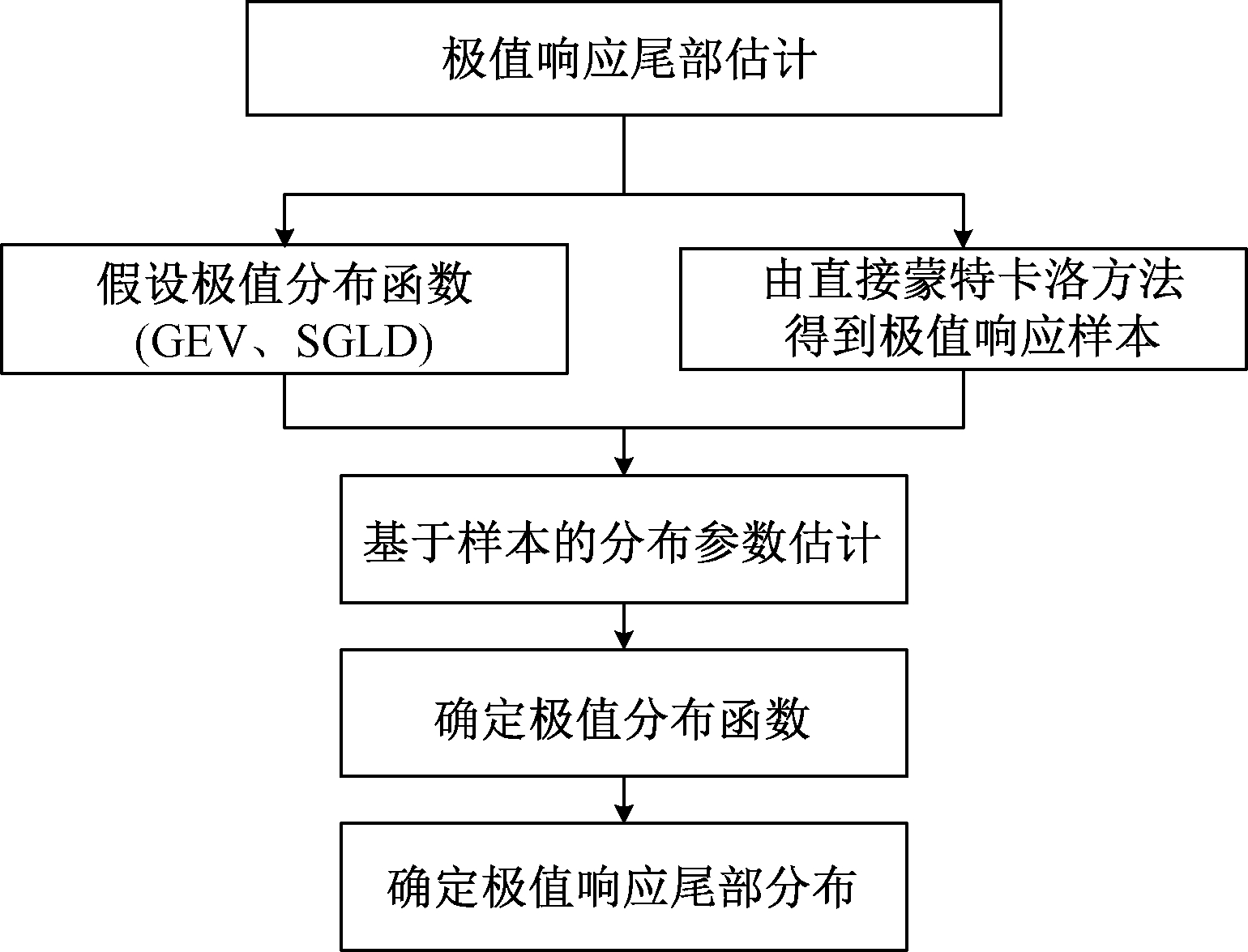
图1 加速模拟方法流程图
Fig.1 Flow chart of accelerated simulation method
2 GEV分布及其参数估计
令m个离散时间点处结构随机响应Y(t)的值为Y1,Y2，…,Ym，则
构成随机序列.定义的极值Mm=max {Y1,Y2，…,Ym}，则Mm即为结构随机响应Y(t)的极值，也即极限状态函数中的S.考虑平稳过程Y(t)，根据极值理论，若Y1,Y2，…,Ym是独立的，或者，虽然为相依的，但满足条件D(u)和D(um)[8]，那么，概率P[(Mm-bm)/am<y]渐进服从广义极值分布G(y)：
(1)
式中：μ∈R、σ>0和ξ∈R分别为位置参数、尺度参数和形状参数.
GEV函数的定义域为{y:1+ξ(y-μ)/σ>0}.当ξ趋于0时，G(y)趋于Gumbel分布.
目前存在多种GEV的参数估计方法，在其加速模拟方法中，Grigoriu等采用了最大似然法进行参数估计.GEV的对数似然函数为：
(2)
式中：nb为响应样本数.
当ξ=0时，上述似然函数可以简化为：
nblg σ.
(3)
使似然函数取最大值的参数μ、σ、ξ值为GEV分布参数的最大似然估计.
需要说明：在笔者采用的数学软件Mathematica中，不需要确定参数am和bm，直接由独立样本估计P(Mm<y)=G(y)确定分布参数.
3 SGLD及其参数估计
移位广义对数正态分布(SGLD)由移位对数正态分布和指数幂分布构成，用于近似具有一定偏态系数和峰度系数的分布[9].因此，适用于近似结构极值响应的分布.SGLD的累积分布函数：
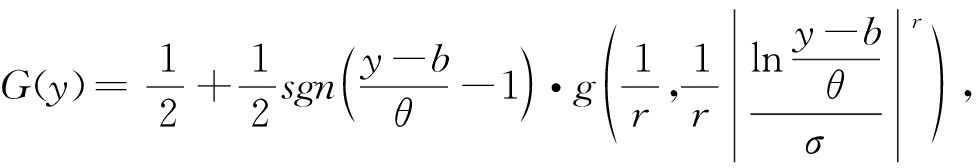
b<y<∞,
(4)
式中：b为位置参数；θ为尺度参数；σ、r为形状参数.
虽然SGLD有4个参数，但独立参数只有σ和r，因为b和θ可由参数σ和r的值确定[9].为了有效估计参数σ和r，确保尾部估计的精确性，He等提出了一个两支撑点方法.两支撑点方法假设由样本估计出极值响应的两个较大超越概率P1=0.1和P2=0.01及其响应样本点y1和y2，从而得到下面的非线性方程：
(5)
(6)
利用参数σ和r与b和θ的关系式，由迭代方法求解方程(5)和(6)，可得到SGLD的参数估计值，进而得到结构极值响应的近似分布SGLD.因为可由较少的响应样本估计概率P1和P2，因此，提高了结构极值响应及其分布尾部的估计效率，加速了随机模拟的收敛速度.
4 两种加速模拟方法的有效性调查
4.1 调查研究1
定义结构响应过程为Y(t)，由m个离散时间点处的响应值构成序列
极值Y=Mm=max{Y1,Y2,…,Ym}，验证序列{Yi}为独立同分布序列时加速模拟方法,估计响应极值分布的可行性及有效性.当独立同分布序列{Yi}的边缘分布为已知分布时，容易得到极值的理论分布，对比分析两种加速模拟方法所得到响应极值的近似分布尾部.
若假设独立同分布序列
的边缘分布分别为高斯分布、指数分布、柯西分布，其累积概率函数F(y)分别为
1-exp(-y)、1/2+(1/π)tan-1 y，则可以得到极值分布概率P(y;m)=P(max1≤i≤m{yi}<y)=P(Mm<y)的理论解为F(y)m.当m趋近于无穷时，F(y)m收敛于0或1，为了避免极限分布的退化，通过适当规范化即引入规范化常数列am>0、bm>0，使得P((Mm-am)/bm<y)为非退化分布，即P[(Mm-am)/bm<y]=F(bmy+am)m为精确解[8].规范化常数列am和bm依赖于边缘分布类型与m大小，当边缘分布分别为高斯分布、指数分布、柯西分布时，其规范化系数am=(2ln m)-1/2和bm=1/am-(1/2)am(ln(ln m)+ln 4π)；am=1和bm=ln m；am=1/tan(π/m)和bm=0.
根据极值定理可得，当m充分大时，对于独立同分布序列，其概率P[(Mm-bm)/am<y]渐进服从广义极值分布G(y),其中am>0、bm>0为规范化序列,如上可得，G(y)与序列边缘分布有关，当边缘分布为高斯分布和指数分布时，G(y)为exp[-exp(-y)]，当为柯西分布时，G(y)为exp(-1/y).由此可得，P(Mm<y)渐进于广义极值分布的理论参数值.P(Mm<y)的理论值和估计值如表1所示.
表1 基于样本和通过极值理论得到P(Mm<y)的估计值及理论值
Tab.1 Based on the sample and the extreme value theory the estimate and the theoretical value of P(Mm<y)
分布类型μσξ理论值估计值理论值估计值理论值估计值高斯分布3.116 53.087 40.269 00.298 20-0.089 5指数分布6.907 86.887 91.000 01.001 400.014 7柯西分布318.470-320.243318.470325.4401.0001.014
采用基于广义极值分布(GEV)假定的加速模拟方法估计独立同分布序列的极值分布，假设极值分布服从广义极值分布(GEV)，通过Monte Carlo的加速模拟方法估计响应极值分布，假设极值分布服从移位广义对数正态分布(SGLD)，通过Monte 模拟得到nb组独立的序列值
为序列离散点个数，得到nb个独立的Mm=max{Y1,Y2,…,Ym}极值样本.在结构极值响应估计中，nb代表结构响应过程样本函数的个数，m代表在m个离散时间点上记录样本函数的响应值.选取nb=2 000，m=1 000，然后通过参数估计方法得到P(Mm<y)参数估计值，如表1所示.由表1中可以看出，通过小样本得到参数估计值与理论近似解十分吻合.
采用基于移位广义对数正态分布(SGLD)假定Carlo模拟得到nb=2 000个响应极值样本，然后估计分布参数，如表2所示.
表2 基于样本得到P(Mm<y)为SGLD的参数值
Tab.2 Based on the sample the parameter values of SGLD of P(Mm<y)
分布类型σrθb高斯分布0.483 03.200 90.740 42.428 7指数分布1.566 80.250 34.480 02.833 3柯西分布————
最后，图2给出了当边缘分布为高斯分布、指数分布、柯西分布时极值分布的精确解和基于广义极值分布(GEV)、移位广义对数正态分布(SGLD)假定的加速模拟方法、基于20 000个样本的Monte Carlo方法的对比结果.
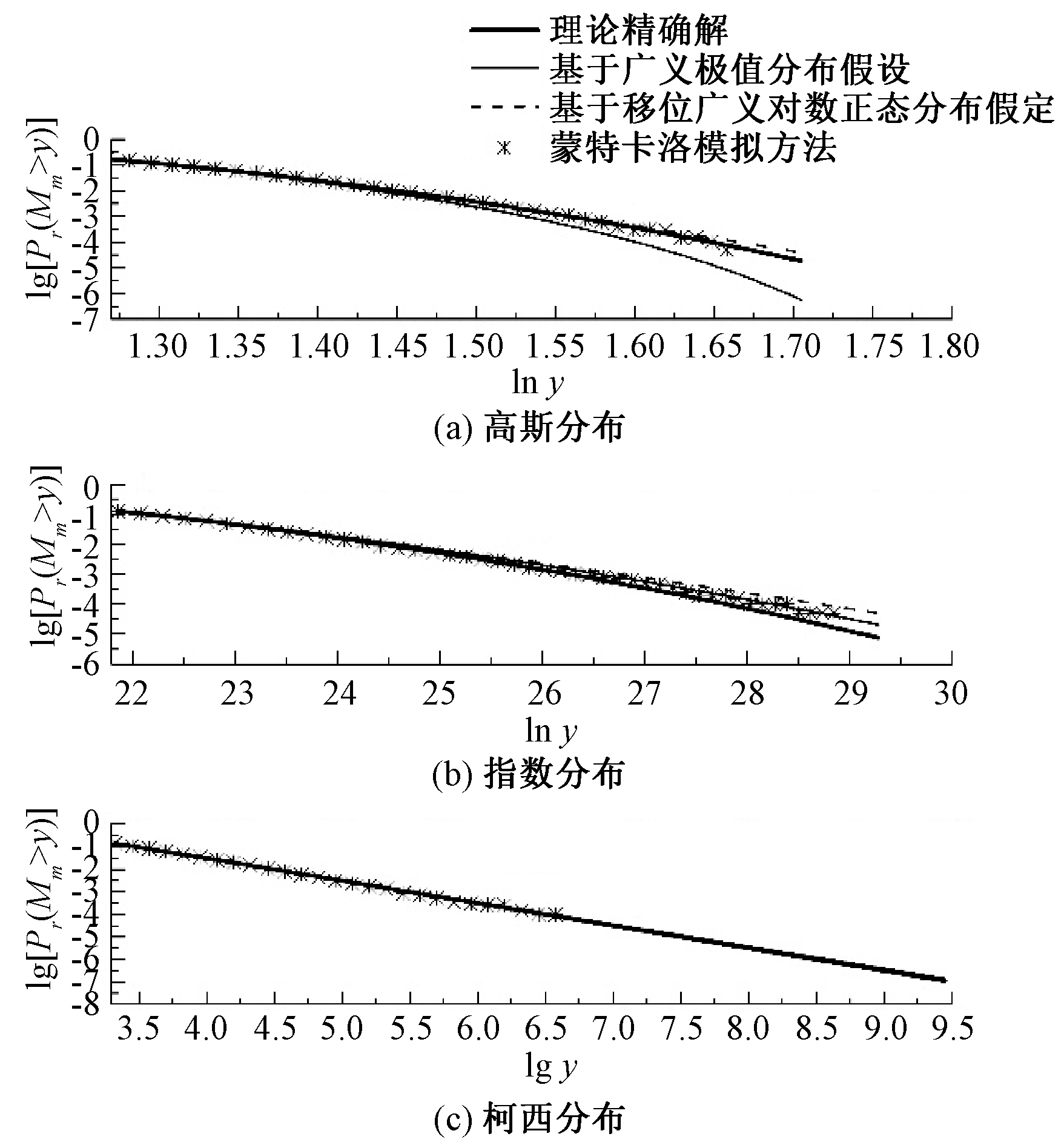
图2 加速模拟方法、蒙特卡洛方法和理论精确解的对比结果
Fig.2 The comparison between accelerated simulation methods and MC method and exact probability
图2中结果表明，两种加速模拟方法对于理想平稳过程的极值估计在尾部区域内有着较好的计算精度和效率.而GEV模型对边缘分布为高斯分布时拟合较差，其余分布结果较好，特别是对于柯西分布，与理论分布基本一致.而SLGD模型对于尾部情况较GEV模型更好，但是无法得到边缘分布为柯西分布时的分布参数，其加速模拟方法都有各自适用范围.
4.2 调查研究2
验证线性振子在随机激励作用下加速模拟方法拟合响应极值分布的精确性及有效性.考虑单自由度线性振子受到高斯白噪声激励作用，采用加速模拟方法得到振子位移响应及绝对值的极值分布尾部，然后与通过直接Monte Carlo模拟得到分布尾部对比.
取Y(t)为结构位移响应，该结构动力方程定义为：
(7)
式中:w0=π；ζ0=0.05；激励输入f(t)是谱密度为
的高斯白噪声.
取结构随机响应Y(t)的持续时间t=20，间隔时间t=0.02，ti+1=ti+t，取m=20/0.02=1 000个离散时间点处Y(t)的值及绝对值构成序列和
定义响应极值Y=Mm=max (Y1,Y2,…,Ym)或Y=max (|Y|1,|Y|2,…,|Y|m)，则可得结构响应及响应绝对值的失效概率分布为P(y;m)=P(Mm>y).取nb组独立的结构响应样本函数Yi(t)(i=1,2,…,nb)，则可以得到nb个独立的极值样本.
在白噪声激励作用下，经历足够长的时间后，结构位移响应方差由小变大，最后趋于稳定，结构位移响应Y(t)由非平稳过程过渡到平稳过程.m个离散时间点处结构随机响应Y(t)的值构成平稳序列，但Y1,Y2,…,Ym之间存在相依关系.当Y(t)进入到平稳过程后，其自相关函数为:
Ry(τ)=πS0e-ζw0τ[cos(wdτ)+
(8)
式中：w0为振子固有频率；wd为有阻尼固有频率；ζ为阻尼比；S0为谱密度.由于Y(t)为高斯过程，对于τ→∞，可得Ry(τ)lg τ→0，可得序列{Yi}满足D(u)和D(um)[8]，可得位移响应极值分布渐进于广义极值分布.采用基于广义极值分布假定的加速模拟方法估计响应Y(t)的极值分布，通过Monte Carlo模拟得到2 000个极值响应样本，然后通过参数估计方法得到广义极值分布参数，如表3所示.
表3 广义极值分布的参数值
Tab.3 The parameter values of GEV
样本序列样本数量μσξ{Yi}2 0000.104 7-0.125 70.027 1{Yi}2 0000.113 6-0.107 30.027 7
对于位移响应绝对值，由于无法得到较长时间后随机响应过程的自相关函数的表达式，不能直接给出序列{|Y|i}是否满足D(u)和D(um).于是在采用基于广义极值分布假定的加速模拟方法估计响应Y(t)绝对值的极值分布，首先假设响应绝对值的极值分布服从广义极值分布，同样，通过Monte Carlo模拟得到nb=2 000个极值响应样本，然后通过参数估计方法得到广义极值分布参数值，如表3所示.
采用基于移位广义对数正态分布(SGLD)假定的加速模拟方法估计响应极值分布，假设极值分布服从移位广义对数正态分布(SGLD)，通过Monte Carlo模拟得到nb=2 000个位移响应极值样本及位移响应绝对值极值样本，然后估计分布参数，具体数据如表4所示.
最后，图3对比了基于广义极值分布(GEV)、移位广义对数正态分布(SGLD)假定的加速模拟方法估计线性振子响应，如图3(a)所示，响应绝对值极值分布结果与基于20 000个样本的Monte Carlo结果，如图3(b)所示.
表4 移位广义对数正态分布的参数值
Tab.4 the parameter of SGLD
样本序列样本数量σrθb{Yi}2 0000.101 951.591 7-1.382 41.499 4{Yi}2 0000.020 61.469 4-1.293 61.401 3
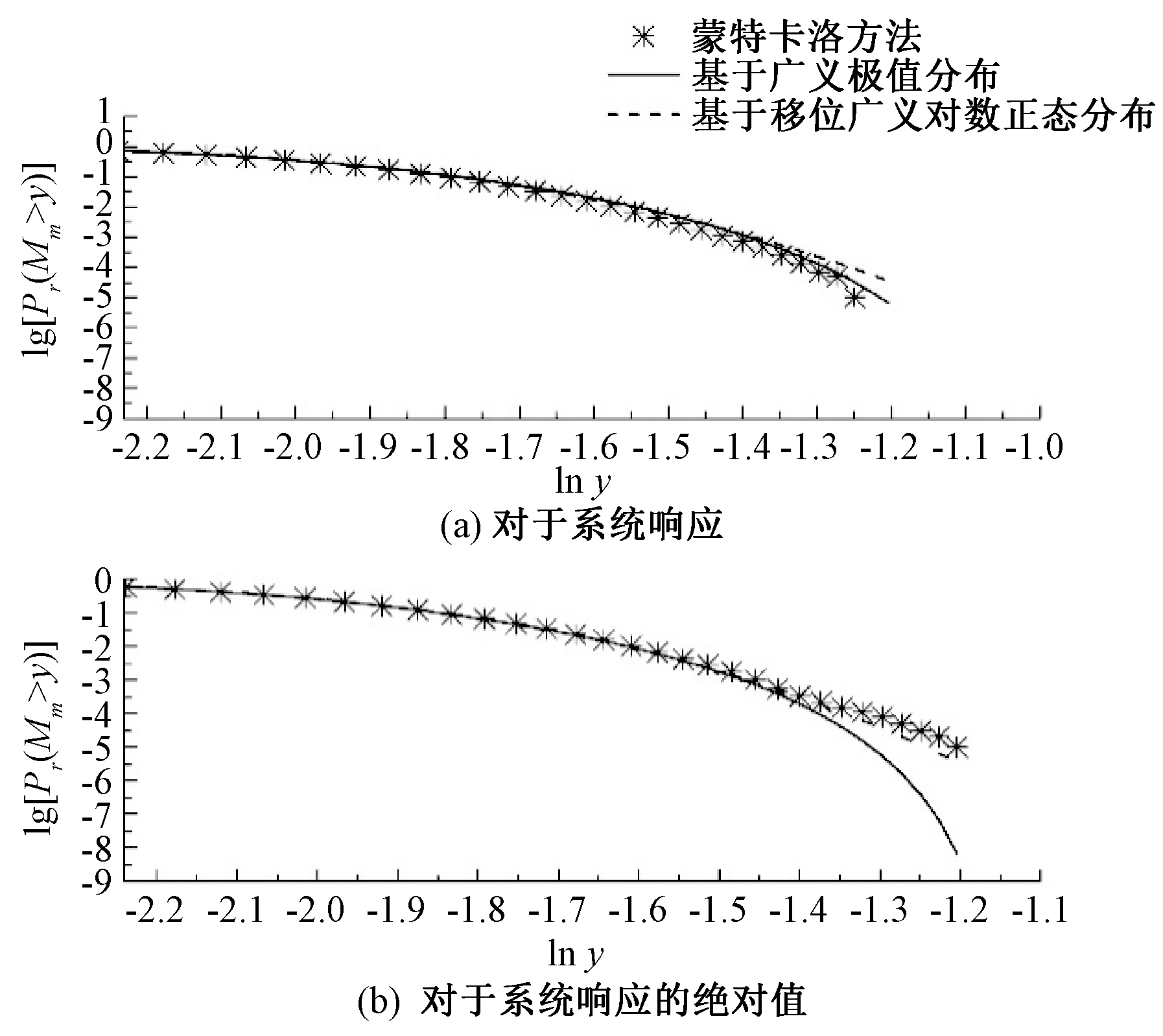
图3 加速模拟方法估计线性振子响应极值分布与蒙特卡洛方法对比结果
Fig.3 The comparison between caccelerated simulation methods and MC method for estimating the extreme distribution of linear oscillator response
图3表明，两种加速模拟方法对于线性结构下受随机激励作用的结构响应极值估计有较好的效率和精度，SGLD模型与极值分布尾部有着更好的拟合.对于随机响应为平稳过程时，且无论是否满足相依关系，从拟合结果来看，GEV模型都与极值分布拟合较好.
4.3 调查研究3
验证非线性单自由度振子在随机地震激励作用下加速模拟方法拟合响应极值分布的精确性及有效性.考虑非线性单自由度振子受到Kanai-Tajimi随机地震波激励作用，采用加速模拟方法得到振子位移响应及响应绝对值的极值分布尾部，然后与通过直接Monte Carlo模拟得到分布尾部对比.
其结构动力方程为:
(9)
式中：Y(t)为结构位移响应；w0=π；ζ0=0.05.层间滞变恢复力fs定义为:
fs=k[αY+(1-α)Z],
(10a)
(10b)
式中：α=0.05代表非线性参数；k=π2；Y和Z分别为层间弹性和滞变位移，Z由Bouc-Wen滞变法则定义；
取层间屈服位移xy为0.75.
取f(t)为Kanai-Tajimi随机地震波激励，其功率谱密度函数为:
(11)
式中:S0=0.016 7；wf=15.7；ζf=0.6.
取持续时间t=20，每隔Δt=0.02取结构响应Y(t)值及绝对值构成响应序列{Yi}和{|Y|i}，通过Monte Carlo模拟得到数量nb=2 000组结构反应值序列{Yi}和{|Yi|}，最后得到2 000个响应及响应绝对值的极值样本.分别采用基于移位广义对数正态分布(SGLD)和广义极值分布(GEV)假定的加速模拟方法估计响应极值分布，假设极值分布分别服从广义极值分布(GEV)和移位广义对数正态分布(SGLD)，通过样本估计方法得出GEV和SGLD参数，如表5、6所示.
表5 广义极值分布的参数值
Tab.5 The parameter values of GEV
样本序列样本数量μσξ{Yi}2 0000.246 60.062 8-0.132 4{Yi}2 0000.267 30.059 6-0.124 8
表6 移位广义对数正态分布的参数值
Tab.6 The parameter values of SGLD
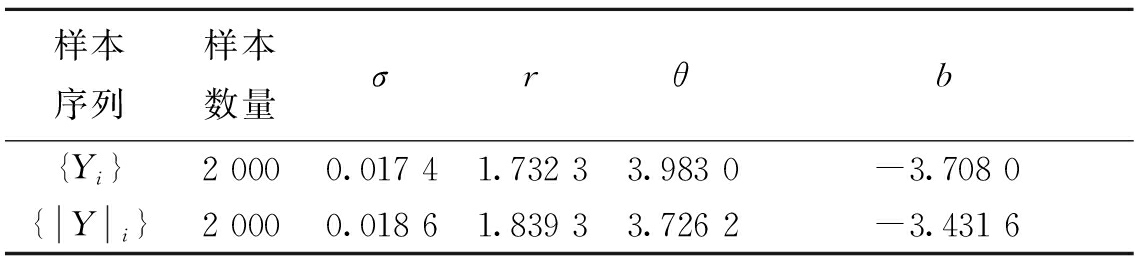
样本序列样本数量σrθb{Yi}2 0000.017 41.732 33.983 0-3.708 0{Yi}2 0000.018 61.839 33.726 2-3.431 6
最后，图4对比了基于广义极值分布(GEV)、移位广义对数正态分布(SGLD)假定的加速模拟方法估计非线性振子响应，如图4(a)所示，响应绝对值的极值分布的结果与基于20 000个样本的Monte Carlo结果，如图4(b)所示.
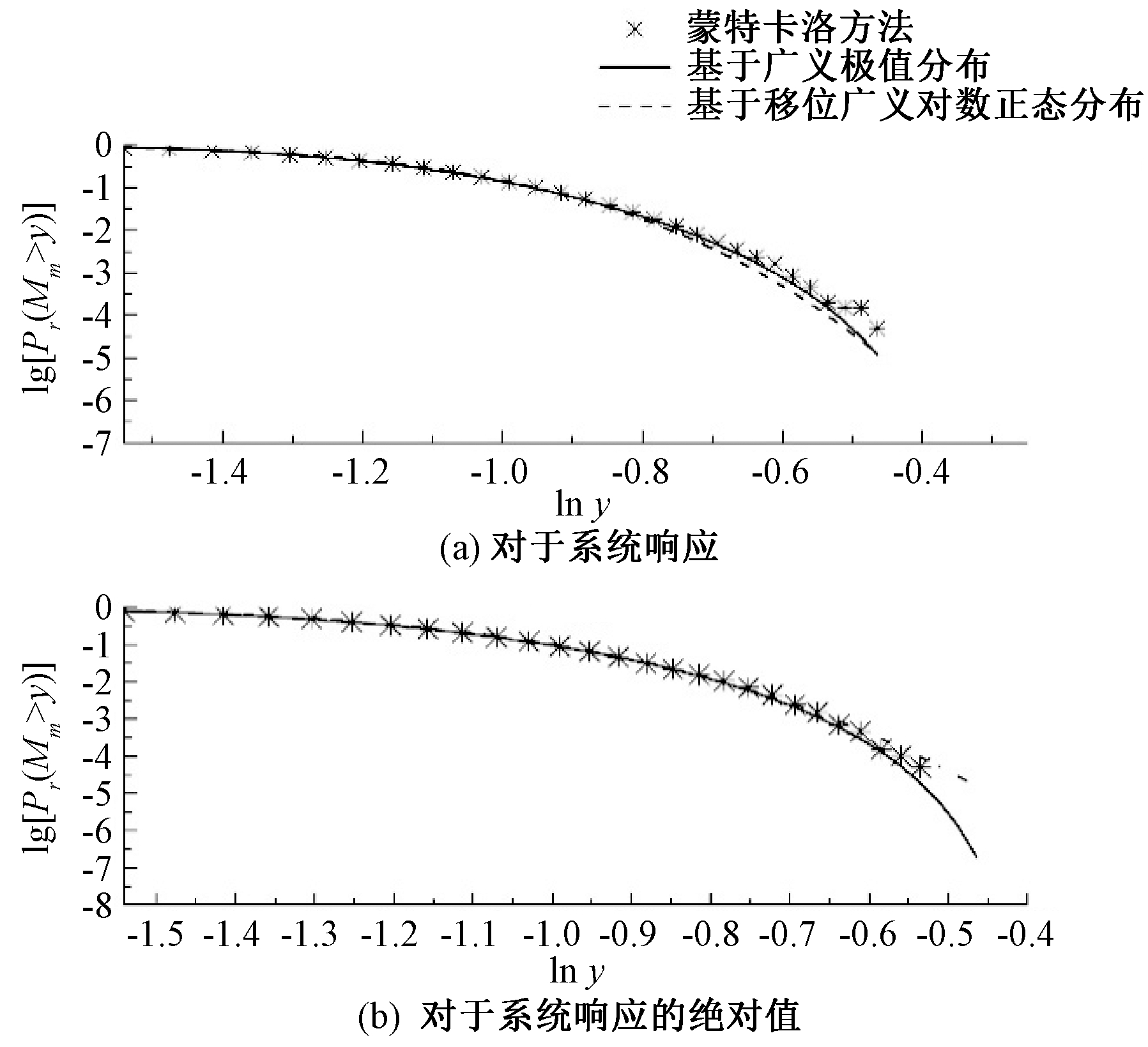
图4 加速模拟方法估计非线性振子响应极值分布与蒙特卡洛方法对比结果
Fig.4 The comparison between accelerated simulation methods and MC method for estimating the extreme distribution of nonlinear oscillator response
图4表明，两种加速模拟方法对于非线性结构下受随机激励作用下的结构响应极值估计也有较高的效率和精度，显示了两种方法适用广泛，其中SGLD模型显示了更好的计算精度.而采用广义极值分布的加速模拟方法，虽然无法确定响应是否满足广义极值分布的适用条件，且未能解决不满足相依关系的平稳过程的极值分布估计的理论问题，但是尾部拟合情况依然较好，仍可以建议作为极值分布估计的有效方法.
5 结论
笔者对比分析了基于广义极值分布和移位广义对数正态分布的加速模拟方法，验证了两种方法在解决估计结构响应极值分布的有效性，避免了直接蒙特卡洛模拟中计算费用过大和效率过低的问题.通过理想分布和单自由度振子模型，证明了该方法能高效地达到微小失效概率至10-3～10-6，满足结构设计及可靠度研究要求，适用于一般结构随机振动问题，具有广泛的工程适用性.通过理论和应用的研究，得到的主要结论有：
(1)笔者通过分析两种加速模拟方法，GEV模型和SGLD模型相比于直接蒙特卡洛模拟，效率能达到10倍以上，计算精度在10-3以上，其两种方法均适用于结构随机响应极值分布尾部估计.
(2)GEV模型基于极值定理，对满足一定条件的序列极值分布有着严格的理论证明，对于一般情况，无法给出完整的理论分析证明，但是从笔者分析发现，GEV对一般情况仍有较好的计算精度与效率.SGLD模型是根据SGLD分布能拟合多种分布，以此来拟合极值分布.
(3)在对结构响应极值分布估计中，在同等计算效率下，SGLD精度优于GEV，而且不受条件限制，但对于样本方差过大、均值过大的特殊情况，无法得出分布参数.
[1] 赵国藩. 工程结构可靠性理论与应用[M]. 大连：大连理工大学出版社，1996.
[2] SHINOZUKA M. Monte Carlo solution of structural dynamics[J]. Computers and Structures, 1972, 2: 855-874.
[3] NAESS A, GAIDAI O. Monte Carlo methods for estimating the extreme response of dynamical systems[J]. Journal of engineering mechanics, 2008, 134(8): 628-636.
[4] BALESDENT M, MORIO J, MARZAT J. Kriging-based adaptive importance sampling algorithm for rare event estimation[J]. Structural safety, 2013, 44: 1-10.
[5] TAFLANDIS A A, CHEUNG S H. Stochastic sampling using moving least squares response surface approximations[J]. Probabilistic engineering mechanics, 2012, 28: 216-224.
[6] GRIGORIU M, SAMORODNITSKY G. Reliability of dynamic systems in random environment by extreme value theory[J]. Probabilistic engineering mechanics, 2014, 38: 54-69.
[7] HE J, GONG J H. Estimate of small first passage probabilities of nonlinear random vibration systems by using tail approximation of extreme distributions[J]. Structural safety, 2016, 60: 28-36.
[8] MICHAELOV G, LUTES LD, SARKANI S. Extreme value of response to nonstationary excitation[J]. Journal of engineering mechanics, 2001, 127(4): 352-63.
[9] HE J. Approximate method for estimating extreme value responses of nonlinear stochastic dynamic systems[J]. Journal of engineering mechanics,2015, 141(7): 04015009.