0 引言
伴随着交通运输业的快速发展,道路修筑有时不可避免地穿越采空区,由此引发的路基不均匀沉降变形、路面开裂等问题,严重威胁行车安全[1].上世纪80年代以来,逐步有专家学者对采空区自身的稳定性开展研究,由于影响因素复杂,多偏重于初步的定性分析.随着软件技术的发展,越来越多的学者利用数值模拟软件对采空区自身稳定性进行研究.Seryakov[2]基于初始应力法,给出了估算采空区围岩状态的方法;宋卫东等[3]利用采空区探测系统(CMS)对采空区进行了精密探测,建立了三维数值计算模型,对采空区群区域的应力场、位移场进行了分析;李真等[4]利用3DMINE、MIDAS及FLAC3D等软件,建立了矿山复杂三维可视化数值分析模型,对松江铜矿采空区进行稳定性分析及安全分级.然而,由于采空区自身稳定性的评价方法受限于目标工程的唯一性,不同的地质结构及围岩状态导致了研究应用的局限性.近些年,随着采空区对新建道路的影响日益突出,越来越多的学者选择以道路为研究主体,简化对采空区自身稳定性的模拟,利用数值模拟计算分析下伏采空区对路基的影响.韩庆哲[5]运用蠕变本构模型,分析采空区三围尺寸等对路基路面变形的影响.张淑坤等[6]建立了复杂荷载条件下采空区顶板-矿柱体系流变力学模型,对高速公路与采空区相互作用影响进行了数值模拟分析; 赵子锋等[7]采用理论研究、现场勘察、模型试验和数值模拟相结合的方法,对高速公路下伏急倾斜采空区路基稳定性进行研究.总体而言,下伏采空区对道路影响的研究仍处于起步阶段,研究内容多样,采空区与道路相对位置对路基稳定性影响的研究尚未深入,且多为经验性措施,不能较好地反映采空区地质变形特征,数值计算的合理性与准确性有待提高.
河南省S323线位于郑州市南部,全长85.574 km,采用双向四车道一级公路标准建设,路基宽24.5 m,设计速度80 km/h.笔者结合新密关口至登封张庄段改建工程,依据实际地质条件,考虑下伏采空区与路基的相对位置,采空区不同沉降期因素,采用改进蠕变本构模型进行数值模拟,得到了不同工况下公路下伏采空区路基沉降及路面水平变形特点,推导了适用于下伏采空区路基沉降预测模型,给出道路修筑的临界安全区域范围.
1 下伏采空区路基沉降变形数值分析
1.1 计算模型
根据设计资料和施工现场实地勘察情况,采用FALC3D软件建立数值计算模型,参数设置如下.
(1)采空区过渡路面结构参数.上面层:50 mm中粒式改性沥青混凝土(AC-16C);
下面层:80 mm粗粒式改性沥青混凝土(AC-25C);
下封层:8 mm热喷改性沥青同步碎石封层;
底基层:400 mm厚级配碎石.
(2)数值模型几何尺寸参数.地基部分:宽356 m,高180 m,沿路线方向长50 m;
路基部分:路基顶宽24.5 m,高4 m,1∶1.5边坡,路基左侧离地基左边界100 m,路基右侧离地基右边界220 m;
采空区几何尺寸:长50 m,宽50 m,高3 m.
(3)边界条件设置.地表为自由边界;左右两侧边界约束横向位移;前后两侧边界约束纵向位移;底部边界约束横向、竖向位移.
1.2 本构关系
岩土工程计算分析中,摩尔-库伦、德鲁克-普拉格等模型应用较为广泛,但是下伏采空区的路基沉降变形随时间发展变化的特点是该类本构模型无法反映的.笔者将摩尔-库伦塑性破坏准则引入到伯格斯蠕变模型[8],这样不仅适用于时间效应的影响,也考虑了岩石材料的黏弹性和黏塑性 [9-10].
1.3 材料参数
路基路面结构材料基本参数取值见表1和表2.
表1 路基路面结构材料参数
Tab.1 Material parameters of subgrade and pavement
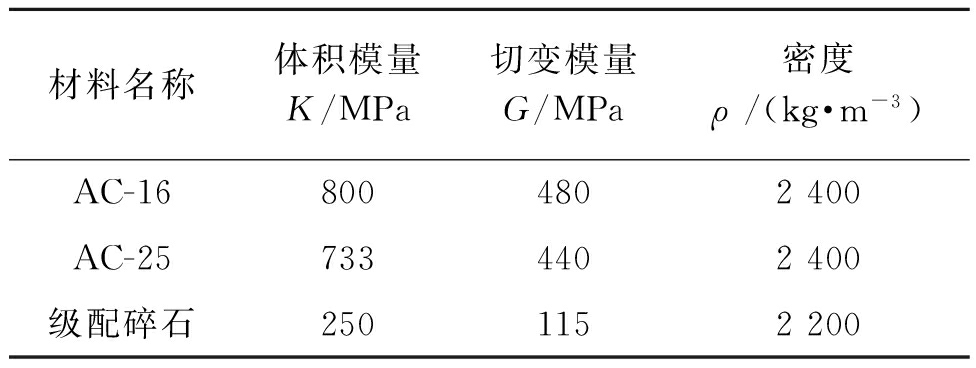
材料名称体积模量K/MPa切变模量G/MPa密度ρ/(kg·m-3)AC-168004802400AC-257334402400级配碎石2501152200
1.4 计算工况
下伏采空区的活跃程度对路基沉降变形的影响显著,根据采空区的形成时间、开采状态等因素,上覆岩体的沉降状态可大致分为瞬时沉降期、活跃沉降期和稳定沉降期.基于采空区地表沉降历时曲线,确定了不同沉降阶段的时间历程,由此设计3种计算工况.
表2 蠕变材料参数表
Tab.2 Creep material parameters
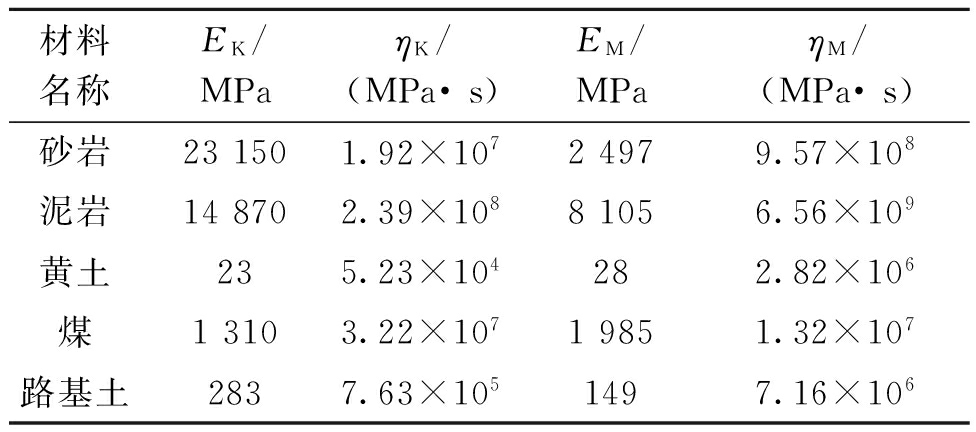
材料名称EK/MPaηK/(MPa·s)EM/MPaηM/(MPa·s)砂岩231501.92×10724979.57×108泥岩148702.39×10881056.56×109黄土235.23×104282.82×106煤13103.22×10719851.32×107路基土2837.63×1051497.16×106
注:Ek、ηK分别为Kelvin模型的切变模量和黏度;EM、ηM分别为Maxwell模型的切变模量和黏度.
工况1:瞬时沉降期,此种工况指修路后立即开采,采空区上覆岩体处于瞬时沉降期,路基沉降变化较为剧烈.设置采空区顶板距路基底面深度分别为50、90、130 m;采空区与路基横向相对位置设计为P1~P6:路基正下方(P1)、采空区左边界与路基右底侧重合(P2)、采空区左边界距路基右底侧20 m(P3)、40 m(P4)、60 m(P5)、80 m(P6).分析采空区和路基不同相对位置对路基沉降的影响.
工况2:活跃沉降期,此种工况指地下开采3个月后筑路,采空区处于活跃沉降期,路基沉降变化稍有减缓.设路基底部距采空区顶板深度为130 m,采空区位置位于路基正下方,计算路基3 a最大沉降量.
工况3:稳定沉降期,此种工况指开采2 a后修路,采空区处于稳定沉降期,路基沉降较为稳定,采空区位置设置同工况2.
1.5 结果分析
(1)采空区活跃状态对路基沉降的影响.当采空区分别处于瞬时沉降期、活跃沉降期和稳定沉降期时修筑道路,3 a后路基沉降对比见图1.
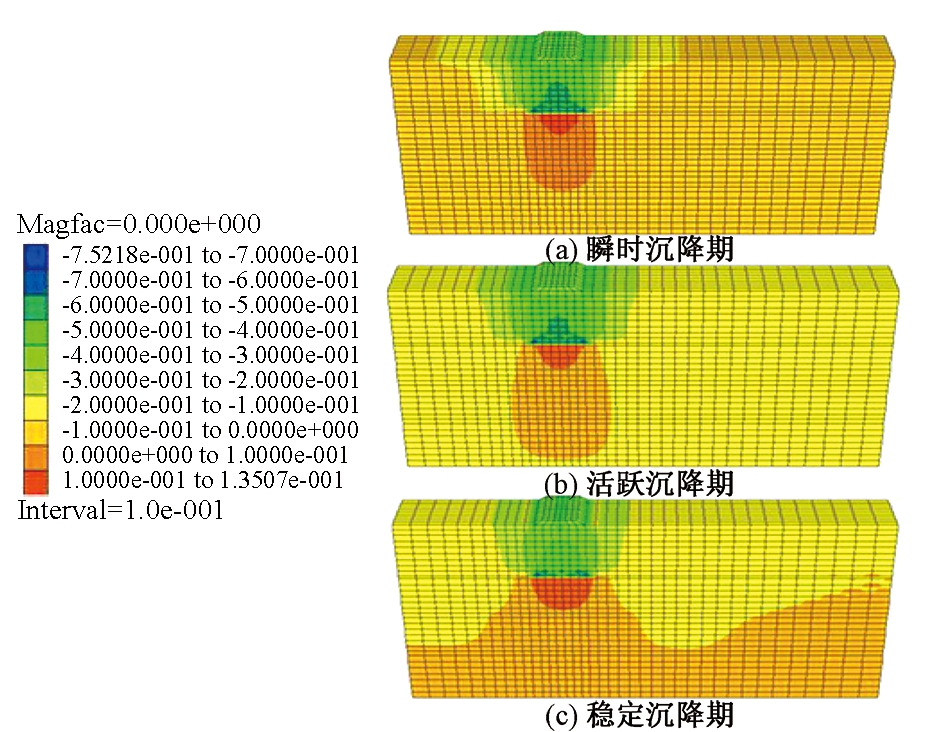
图1 不同沉降期的地基沉降云图
Fig.1 Foundation subsidence chart in different periods
由图1可以得出:在3种不同活跃状态的采空区上方修路时,3 a的最大沉降量分别为752、617、122 mm,最大沉降均处于采空区顶部中心位置.当采空区处于瞬时沉降阶段和活跃阶段时,路基沉降量较大.修筑道路时建议采取必要处治措施或避免此阶段施工.
(2)采空区相对位置对路基稳定性的影响.依据最不利影响原则,计算分析了采空区处于瞬时沉降期情况下,采空区与路基相对位置对道路路基3 a的沉降影响,路面中心沉降与路基两侧边界相对沉降差见表3.通过与路基边界处监测桩的实测沉降数值比较,计算沉降量与实测量变化规律较为一致,沉降量较为吻合,表明了数值计算的可靠性.
表3 路面中心沉降及边界相对不均匀沉降
Tab.3 Settlements of the road center and uneven settlement of subgrade boundaries mm

采深沉降值采空区相对位置P1P2P3P4P5P650m90m130m路面中心点沉降值486.0264.0142.264.628.816.5路基左边界点沉降差值-105.0-88.7-41.1-20.2-8.3-1.3路基右边界点沉降差值-105.060.052.828.16.60.6路面中心点沉降值360.0251.0172.390.650.431.5路基左边界点沉降差值-45.8-71.9-35.6-21.5-10.6-0.9路基右边界点沉降差值-45.548.535.423.219.40.4路面中心点沉降值223.0179.3140.299.764.838.9路基左边界点沉降差值-28.9-61.6-11.8-25.1-12.2-1.1路基右边界点沉降差值-30.128.727.821.6-9.11.3
表3数据表明:当采空区位于道路正下方(P1)时,路面中轴线处沉降最大,采深为50、90、130 m时分别达到486、360、223 mm;当道路跨越或与采空区临界时(P2),路基左右两侧边界的不均匀沉降差值最大.此外,在此两种工况下,采深为50 m所引起的路基沉降值相对于采深为130 m时的沉降值增加1倍以上.沉降量过大或不均匀沉降轻则导致路面弯曲、开裂,重则造成塌陷、断裂等破坏.因此,应尽量不在采空区正上方或部分重合区域修建道路,若无法避开,则必须进行处置,预防采空区塌陷,提高路基路面的抗变形能力.当采空区边界距路基底侧20 m(P3)以外时,路面整体沉降和不均匀沉降明显降低,此时采深对路基沉降值的影响不起主导作用,在实际设计和施工时,可采用合理的措施减少采空区对道路造成的危害.当采空区边界距路基底侧80 m(P6)以外时,采空区对道路的影响大大减小,采深对路基沉降值的影响进一步降低.不同位置的采空区引起的路面水平位移见表4.
从表4可以得出:路面水平位移随采深增大而减小,且两侧边界水平位移差值也相应减小.当采空区处于路基正下方,路面两侧边界向中轴线移动;当采空区边界分别与路基底侧临界,相距20、40、60 m时,随着采空区与道路水平相对距离增加,路面中心点和边界水平位移减少,逐渐趋于稳定;当道路距离采空区80 m时,路面中心点水平位移基本在5 mm以内,采空区的影响基本可以忽略.
表4 路面水平位移
Tab.4 Horizontal displacement of pavement mm
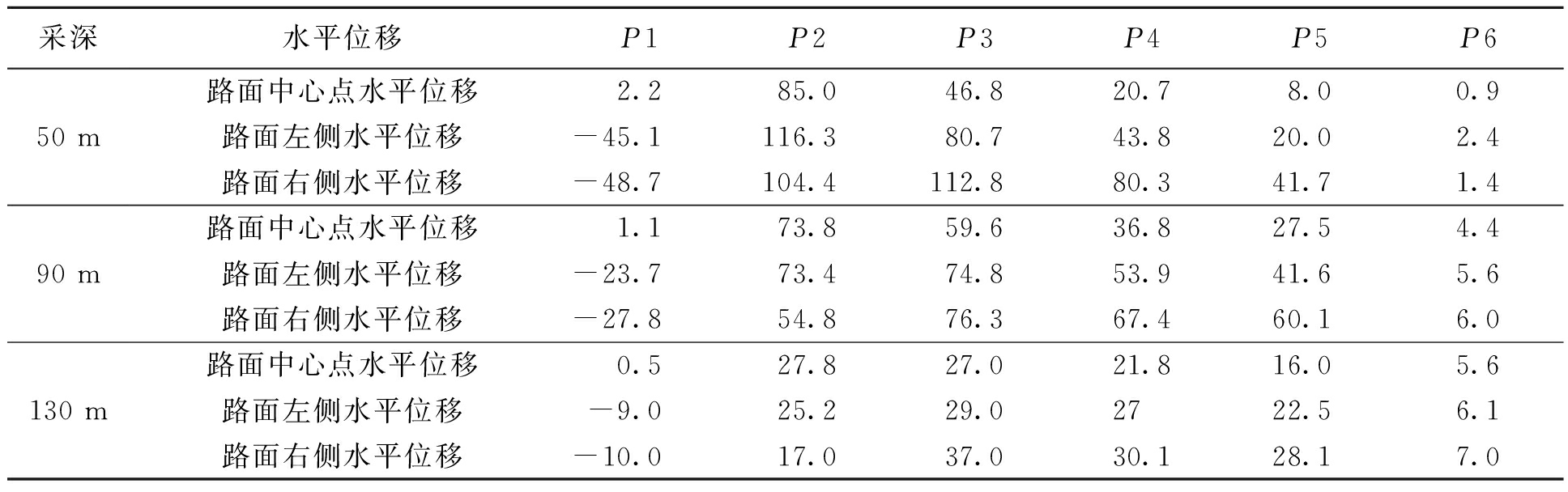
采深水平位移P1P2P3P4P5P650m90m130m路面中心点水平位移2.285.046.820.78.00.9路面左侧水平位移-45.1116.380.743.820.02.4路面右侧水平位移-48.7104.4112.880.341.71.4路面中心点水平位移1.173.859.636.827.54.4路面左侧水平位移-23.773.474.853.941.65.6路面右侧水平位移-27.854.876.367.460.16.0路面中心点水平位移0.527.827.021.816.05.6路面左侧水平位移-9.025.229.02722.56.1路面右侧水平位移-10.017.037.030.128.17.0
(3)下伏采空区道路修筑临界安全区域确定.表3和表4的数据说明,当下伏采空区处于路基向外延伸80 m范围以内采深小于130 m时,路面中心沉降、路基两侧边界相对沉降、路面中心水平位移和道路两侧边界相对水平位移值均不可忽略.超过该范围,以上4项变形指标量值很小,可以忽略采空区对道路造成的影响.因此,确定采空区采深大于130 m距采空区水平相对位置80 m以外区域为道路修筑安全区.
2 下伏采空区路基沉降预测模型
基于上述采空区对路基稳定性的数值分析,为了更好地为道路设计及施工提供科学依据,有效准确地对下伏采空区沉降预测十分重要.通过预测下伏采空区路基不同时期的沉降变形量,了解道路修建过程中路基沉降的基本规律,可以优化施工组织,提高施工效率,保证工程质量.
曲线拟合法是道路路基沉降预测中常用的方法,三点指数曲线法为其中较为常见的方法[11-12].传统的三点指数曲线法不能反映施加的荷载和下伏采空区的瞬时沉降[13].笔者将第一点用来表征瞬时沉降,修正的沉降预测公式如下:
St=S∞-(S∞-S瞬)e-βt,
(1)
式中:St为t时刻的沉降值;S∞为最终稳定沉降值;S瞬为瞬时沉降值;β为与沉降速率有关的参数,
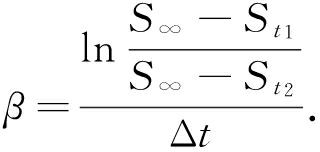
式(1)包含了瞬时沉降的修正指数曲线表达式,三点均由实测数据确定.但由于瞬时沉降在短时间内产生较大的沉降,难以准确监测,因此引入考虑隧洞开挖引起的地表沉降预测的派克公式[14-15]:
(2)
式中:Vl为地层损失率;K为沉降槽宽度;A为开挖隧道的横截面积;y和z表征采空区的位置情况.
将数值模拟结果代入式(2),导出矩形断面采空区影响下的地表瞬时沉降预测公式:
S瞬![]()
(3)
式中:D2/h2表征采空区断面形状的影响(D为采空区宽度,h为厚度).根据参数的取值参考要求[16],结合前文数值计算结果,地层损失率Vl约4.4%.当采深z=50 m时,属浅采空区,K取值0.8;当采深z=130 m时,K取值约0.5.
将式(3)代入式(1),即得到修正后的三点法指数曲线预测模型.由于采空区地质条件复杂多变,该模型适用于采空区形状相对简单,可简化为矩形断面的单个采空区工况,对于长条状或拥有复杂结构形状的采空区、以及多空腔采空区共同作用的工况,计算结果的精度会受到一定影响.本模型计算的路基沉降曲线与所结合工程实测数据对比见图2.
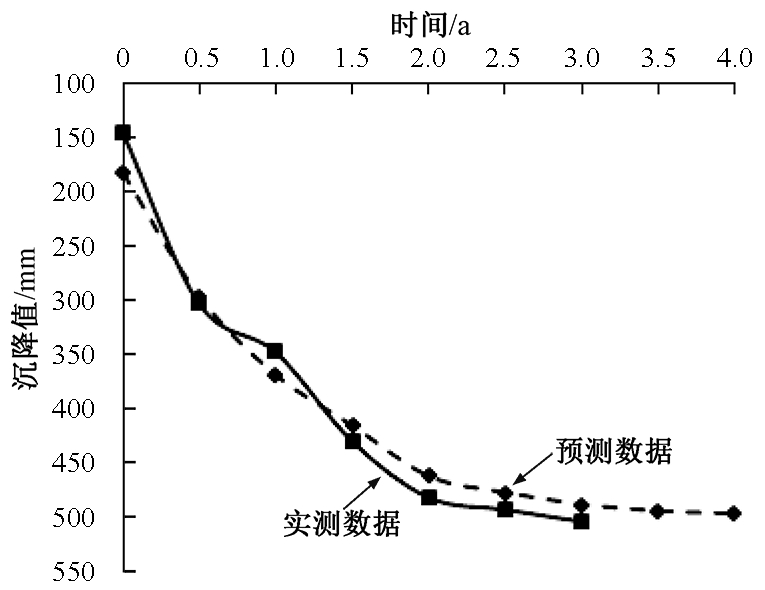
图2 路基沉降-时间曲线图
Fig.2 Time-sedimentation curve of subgrade
由图2可知,预测模型计算的时间-沉降曲线与工程监测的曲线吻合较好,二者整体趋势较为符合,预测模型精度较高,其预测结果可作为采空区道路修筑工程设计和施工时的参考.
3 结论
(1)计算表明处于不同沉降期的采空区对路基沉降的影响显著.当下伏采空区处于瞬时沉降和活跃沉降阶段时,道路沉降变形较大,不宜修筑道路或须对采空区进行必要处治;当采空区处于稳定沉降阶段时,道路沉降及水平偏移量较小,可在施工时采取适当措施减小变形.
(2)通过采空区和路基相对位置对路基稳定性影响的研究,确定道路修筑临界安全区域为距采空区80 m以外区域.建议道路规划设计时,根据开采资料及现场勘察确定下伏采空区位置.
(3)提出了适用于矩形断面下伏采空区的路基沉降预测模型,模型计算结果与工程实测数据吻合较好,可为采空区道路修筑设计和施工提供技术支撑.
参考文献:
[1] 赵德深,范学理.矿区地面塌陷控制技术研究现状与发展方向[J].中国地质灾害与防治学报,2001,12(2):86-89.
[2] SERYAKOV V M. Calculation of stree-strain state for an over-gof rock mass [J].Journal of mining scinece,2009,45(5):420-426.
[3] 宋卫东,付建新,杜建华,等. 基于精密探测的金属矿山采空区群稳定性分析[J]. 岩土力学,2012,33(12):3781-3787.
[4] 李真. 松江铜矿采空区稳定性分析及治理技术研究[D].长沙:长沙矿山研究院,2016.
[5] 韩庆哲.采空区路基路面变形规律的研究[J].道路工程(应用技术版),2014,10(9):32-35.
[6] 张淑坤. 高速公路下伏采空区探测及稳定性研究[D].阜新:辽宁工程技术大学土木与交通学院,2015.
[7] 赵子锋. 高速公路下伏急倾斜采空区勘察技术及对路基稳定影响研究[D].西安:长安大学公路学院,2015.
[8] 袁海平,曹平,许万忠,等.岩石粘弹塑性本构关系及改进的Burgers蠕变模型[J].岩土工程学报,2006,28(6):796-799.
[9] MANICA M, GENS A, VAUNAT J, et al. A time-dependent anisotropic model for argillaceous rocks. Application to an underground excavation in callovo-oxfordian claystone[J]. Computers and geotechnics, 2017,85(5):341-350.
[10] ZUO W L, LU Q J. Study on the constitutive model of visco-elasticity-plasticity considering the rheology of rock mass[J]. Advances in civil infrastructure egineering, 2013,639(9):567-572.
[11] 潘林有,谢新宇.用曲线拟合的方法预测软土地基沉降[J]. 岩土力学,2004,25(7):1053-1058.
[12] 张振武,徐晓宇,王桂尧.基于实测沉降资料的路基沉降预测模型比较研究[J].中外公路,2005,25(4):26-29.
[13] 陈善雄,王星运,许锡昌.路基沉降预测的三点修正指数曲线法[J].岩土力学,2011,32(11):3355-3360.
[14] 韩煊,李宁, STANDING J R.Peck公式在我国隧道施工地面变形预测中的适用性分析[J].岩土力学,2007,28(1):23-28.
[15] 王金明.地铁隧道施工引起的地表沉降及变形研究[D].长沙:中南大学土木建筑学院,2009.
[16] 柳厚祥.地铁隧道盾构施工诱发地层移动机理分析与控制研究[D].西安:西安理工大学土木建筑工程学院,2008.