0 引言
随着三维模型应用领域的不断增加,提高三维模型的共享率和复用率成为当前的研究热点.三维模型检索即从海量三维模型中检索出与某一特定模型相似的所有模型的过程.根据所提取对象的不同,三维模型检索方法分为基于文本的检索方法和基于内容的检索方法.基于文本的检索需要人为地为每个模型添加关键字,它带有很大的主观性;基于内容的检索是根据三维模型的特征进行检索,大大减少了人工干预,是当今的研究热点.
根据提取特征对象的不同,可将检索方法分为3类:基于拓扑结构的检索方法、基于形状的检索方法、基于图像比较的检索方法.基于形状的检索方法在效果上直观且稳定,受到广泛研究.如Ankerst等[1]提出基于形状直方图的特征提取方法;Paquet等[2]用离散小波变换的方法对三维模型的特征进行描述;Osada等[3]提出形状分布算法.单一特征的检索方式不能准确表达模型的信息,基于多特征检索方法融合局部特征和全局特征,成为近年来的研究热点.如Chen等[4]通过融合Zernike矩和傅里叶系数检索三维模型;Vranic等[5]提出基于轮廓、射线和深度信息的描述子;Zou等[6]基于主面分析和群融合提出了联合形状分布描述子;Li等[7]提出一种融合Zernike矩变换、傅里叶变换、深度信息和射线的三维模型检索方法.
虽然三维模型检索效率有明显提高,但仍然存在很多问题,如局部特征点有效性低,影响特征点匹配精度;边缘特征描述方式复杂度高,后续存储量大且计算费时;局部特征不能表达模型的整体信息,特征选择没有统一的标准.针对以上问题,笔者提出基于多特征融合的三维模型检索方法,结合快速计算的ORB特征和精简的形状上下文特征,形成更全面的描述模型信息.对比试验证明本方法有效提升了NN、FT、ST、E测度[8]这4个指标值,P-R曲线也进一步改善,大大提高检索性能.
1 相关知识
1.1 ORB特征
ORB(oriented FAST and rotated BRIEF)是由Rublee等在ECCV2011上提出的一种基于视觉信息的特征点检测与描述算法.它的主要思想是在特征点附近随机选取若干点对,将这些点对的灰度值大小组成一个二进制串,并将这个二进制串作为该特征点的特征描述子.ORB分为提取具有方向的FAST特征点和提取具有旋转不变的BRIEF特征描述子两个过程.ORB特征计算速度快,它的描述子以二进制串形式表示,不仅节约存储空间,也大大缩短了匹配时间.
1.2 Canny算子
Canny边缘检测算子是Canny[9]于1986年提出的一个多级边缘检测算法.边缘部分集中了图像的大部分信息,它主要是对灰度变化的度量、检测和定位,边缘检测需要有效地抑制噪声,且尽量精确地确定边缘的位置,因此边缘特征是很有效的整体特征.
1.3 形状上下文描述子
形状上下文是一种基于轮廓的形状描述子,由Belongie等[10]在2002年提出,是为轮廓上的像素点提供上下文信息的描述子.形状上下文描述子的基本思想[11]:对于给定的一个形状,通过边缘检测子获取轮廓边缘,对轮廓边缘均匀采样得到一组离散的点集P={pi|i=1,2,…,n},依次选取每个采样点作为参考点.以其中任意一参考点p为例,以p为中心建立极坐标系,在以p为圆心R为半径的区域内,按距离和角度划分区域,形成靶状.按照距离和角度统计落入每个区域的点的个数,形成点的分布直方图hp,称为点p的形状上下文.形状上下文描述子是对轮廓特征点的进一步提取,提高了特征表示的准确性和有效性.
1.4 匈牙利算法
匈牙利算法最早是由匈牙利数学家King提出,用于解决二分图的最优匹配问题.1955年Kuhn把上述算法推广用于求解著名的指派问题.算法的基本步骤如下[12]:
(1)对于任意给定的非负系数矩阵A,将其进行变换,使其在各行各列中都出现0元素.
(2)进行试指派,若能够选出n个独立的0元素,就可确定最优置换,程序终止;否则转(3).
(3)迭代:利用最少直线覆盖所有0元素,确定系数矩阵中能够找到的最多的独立0元素个数,并在没有被直线覆盖的部分,确定最小元素x,在被直线覆盖的各行减去x,在被直线覆盖的各列加上x来增减0元素的总数,调转(2).
2 基于多特征融合的三维模型检索
为了更高效且全面地描述模型特征,提出基于多特征融合的三维模型检索方法.对模型多视图投影,分别对每张投影图提取具有尺度不变性的ORB特征和准确统计轮廓分布的形状上下文特征,对ORB特征匹配点反复剔除迭代,并计算形状上下文描述子间的相似度,通过特征融合计算结果.总体框架如图1所示.
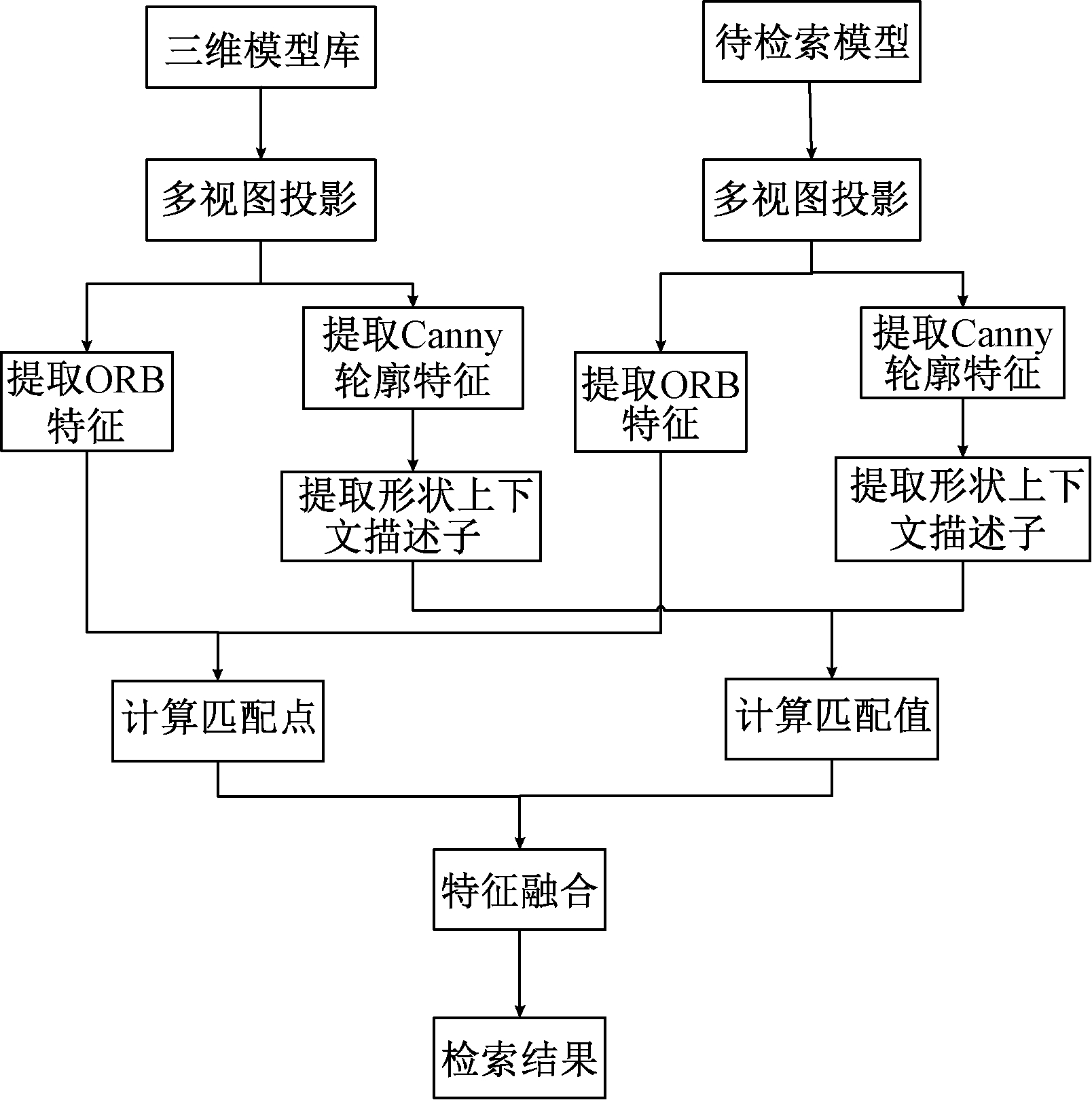
图1 基于形状上下文的多特征三维模型检索方法框架图
Fig.1 The frame of 3D model retrieval method based on shape context
2.1 多视图投影
基于视图投影对三维模型检索是一种很直观的方法.单一角度分析三维模型是片面的,而投影角度过多会造成计算复杂.笔者分析相关文献[13]及对比试验结果,建立三维模型外围72面体,选取38个顶点作为角度,进行视图采样,这38个角度均匀分布于球部空间.避免角度冗余的同时,有效提取模型多个角度的视图信息.选取杯子模型作为示例,如图2所示,对该模型的38个角度进行多视图投影,如图3所示.

图2 杯子模型
Fig.2 Cup model

图3 投影视图
Fig.3 Projection views
2.2 特征提取
分别提取ORB局部特征点、Canny轮廓特征以及形状上下文描述子.
2.2.1 提取ORB特征
ORB由提取FAST特征点和BRIEF特征点描述子两部分组成,并在此基础上进行了改进与优化.
(1)提取FAST特征点.检测候选特征点周围一圈的像素值,如果候选点周围邻域内有足够多的像素点与该候选点的灰度值差别够大,则认为该候选点是一个特征点,定义为:
(1)
式中:I(x)为圆周上任意一点的灰度;I(p)为圆心的灰度;εd为灰度值差的阈值.如果N大于给定阈值,一般为周围圆圈点的3/4,则认为p是一个特征点.再计算特征点的主方向,ORB利用质心来计算,特征点坐标到质心形成的向量作为该特征点特征向量,向量角度θ定义为FAST特征点的方向.
(2)提取BRIEF特征点描述子.在特征点附近随机选取若干点对组成图像块,对它们进行旋转,再把图像块的灰度值二值化后组成一个二进制串,将这个二进制串作为该特征点的特征描述子.它的每一位都是由随机选取的两个二进制点进行比较得来的.如下:S表示随机点位置(2×n的矩阵),Sθ表示旋转后的随机点的位置,计算如式(2).得到新的随机点位置后,利用积分图像进行二进制编码.ORB特征是BRIEF描述子的一种改进,具有旋转不变性、尺度不变性和对噪声的鲁棒性.
Sθ=S×Rθ.
(2)
ORB特征点提取如图4所示,圆圈为检测到的特征点.
2.2.2 提取Canny轮廓特征
对38张视图用Canny算子提取轮廓信息.边缘部分集中了图像的大部分信息,Canny边缘检测算法的步骤如下.
Step 1:用高斯滤波器平滑图像;
Step 2:用一阶偏导的有限差分来计算梯度的幅值和方向;
Step 3:对梯度幅值进行非极大值抑制;
Step 4:用双阈值算法检测和连接边缘.
Canny边缘检测如图5所示,(a)为二维的视图投影,(b)为Canny算子提取到的边缘特征.

图4 ORB特征点提取
Fig.4 ORB feature points detection
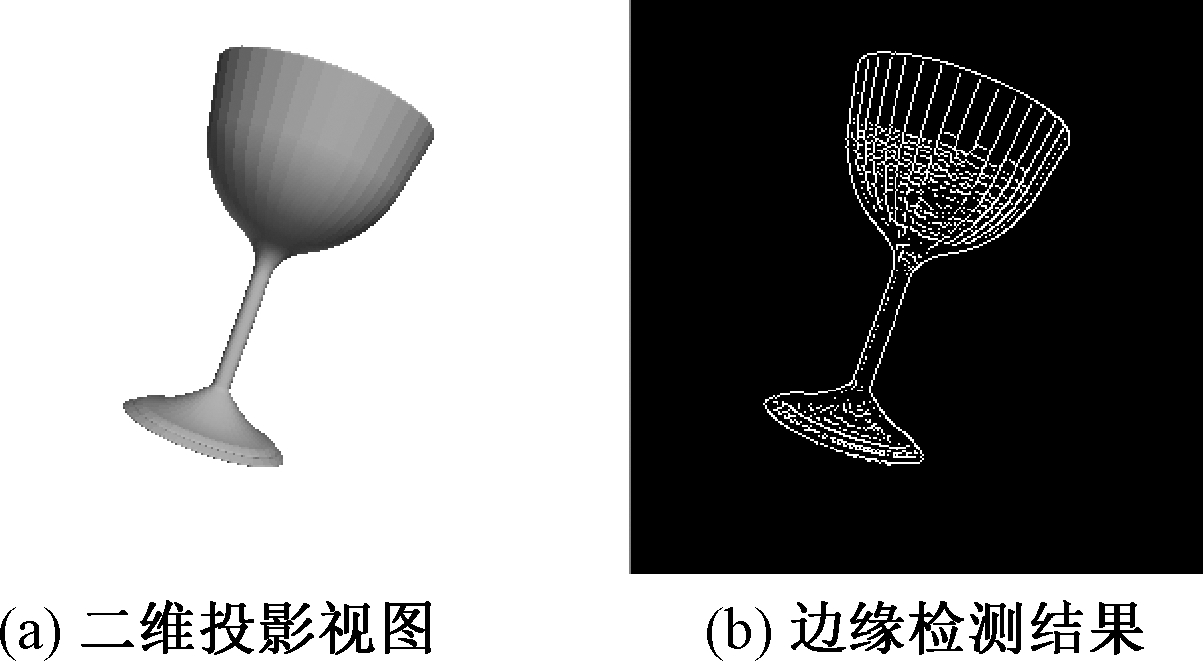
图5 Canny边缘检测
Fig.5 Canny edge detection
2.2.3 提取形状上下文描述子
轮廓不同点处的形状上下文是不同的,但相似轮廓对应点处形状上下文是相似的.点p的特征直方图的计算方法:
(3)
用Canny算子提取模型的轮廓信息后,采集n个代表轮廓点作为采样点,n值的选取范围在100~200之间,对采样点建立形状上下文描述子,区域的划分数量k根据试验对比得到.对每个采样点都可以建立形状上下文描述子,则每一张视图都可以用一个矩阵来表示:
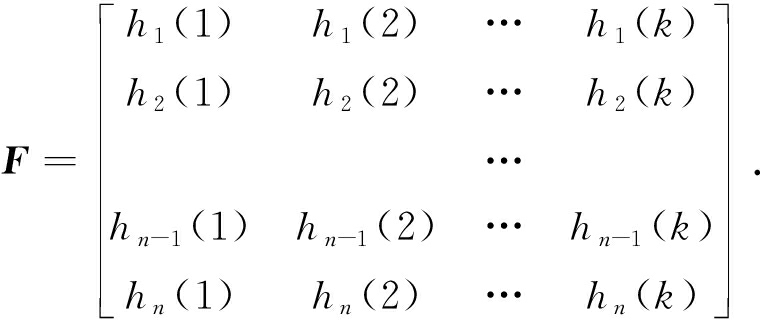
(4)
2.3 计算相似度
2.3.1 计算ORB特征点对
(1) 用匹配器检测特征点对;
(2)设置阈值,剔除距离比例相差过大的匹配点;
(3)判断特征点对之间是不是一一对应关系;
(4)反复迭代消除错误的匹配.
检测模型间特征点对的数量,对视图进行相对应的检测,统计得到两个模型特征点对的总和作为最终的结果.d表示局部特征之间的差异度,m表示两个模型特征点对的个数,d为:
(5)
考虑到两个模型特征点对数可能为0,造成式(5)的分母为0,对式(5)进行修改:
(6)
2.3.2 计算形状上下文描述子相似度
选取形状轮廓上任意点pj、di.hi表示点di的形状直方图,hj表示点pj的形状直方图,k表示区域划分的数量.C(di,pj)表示两个点之间的相似距离,令Cij=C(di,pj),则
(7)
由此可得,两个形状之间的距离为:
(8)
使用匈牙利算法,距离值匹配后的数值最小.
2.4 特征融合
对ORB特征和形状上下文特征的相似度进行融合,形成新的特征相似度D(mi,mj),公式为:
(9)
对ORB特征相似度和形状上下文特征相似度赋予不同的权值,分别是w1和w2,0<w1,w2<1且w1+w2=1.对于相同的模型,相似度为0.
3 试验
3.1 试验环境和数据
硬件环境:Acer Veriton, D4300 Intel(R) Core(TM) i5-3470 CPU @ 3.20 GHz,8 GB内存.
软件环境:64位的Windows 10,MatlabR2012b和Visual Studio 2013.
试验模型库:SHREC2012GTB[13]模型库和普林斯顿大学提供的PSB模型库.
SHREC2012GTB模型库有60个类,总共1 200个模型.PSB模型库有260个类,总共1 814个模型,该库有两个子库组成:训练库和测试库.每组都是907个模型,分别包含90个和92个类,试验是在PSB库的测试集上进行.
3.2 评价标准
采用行业内5种评价标准进行对比试验,分别是:
(1)NN:表示返回的第一个模型属于目标类的比例.
(2)FT:表示返回的前C-1(C为目标类模型的数量)个模型属于目标类的比例.
(3)ST:表示返回的前2(C-1)个模型属于目标类的比例.
(4)E:表示三维模型检索的准确率.
(5)P-R曲线图:表示三维模型检索总体的检索效率.
3.3 试验结果
3.3.1 SHREC2012GTB模型库
本方法3D model retrieval method based on multiple feature fusion(3DMFF)与经典算法LSD-sum算法(LSD)[14]、3D model retrieval method based on fourier and shape fusion算法(3DFSF)[15]、D2 bounding box normal angle area算法(DBNAA-DERE)[13]和3DSP-L2_1000_CHi2算法(3DSP)[16]进行对比试验.前4项指标NN、FT、ST、E的对比结果如表1所示,P-R曲线的对比情况见图6.
表1 SHREC2012GTB模型库上的试验对比
Tab.1 Experiment comparison on SHREC2012GTB database %
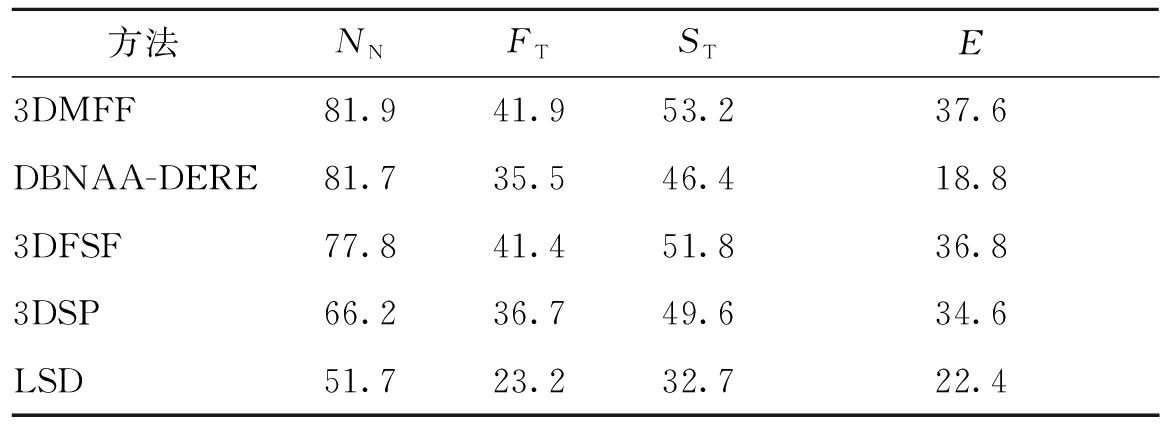
方法NNFTSTE3DMFF81.941.953.237.6DBNAA-DERE81.735.546.418.83DFSF77.841.451.836.83DSP66.236.749.634.6LSD51.723.232.722.4
3.3.2 PSB模型库
本方法3DMFF与经典算法D2形状分布算法(D2)[17]、gaussian euclidean distance transform算法(GEDT)[18]、spherical extent function算法(EXT)[19]和shape histogram算法(SECSHEL)[20]进行对比试验.
前4项指标NN、FT、ST、E的对比结果如表2所示,P-R曲线的对比情况见图7.
通过对比实验表明,本章提出的方法在SHREC2012GTB库上取得相对好的检索效果.融合局部特征和全局特征能够更全面地描述模型信息,大大提高了特征匹配的质量.
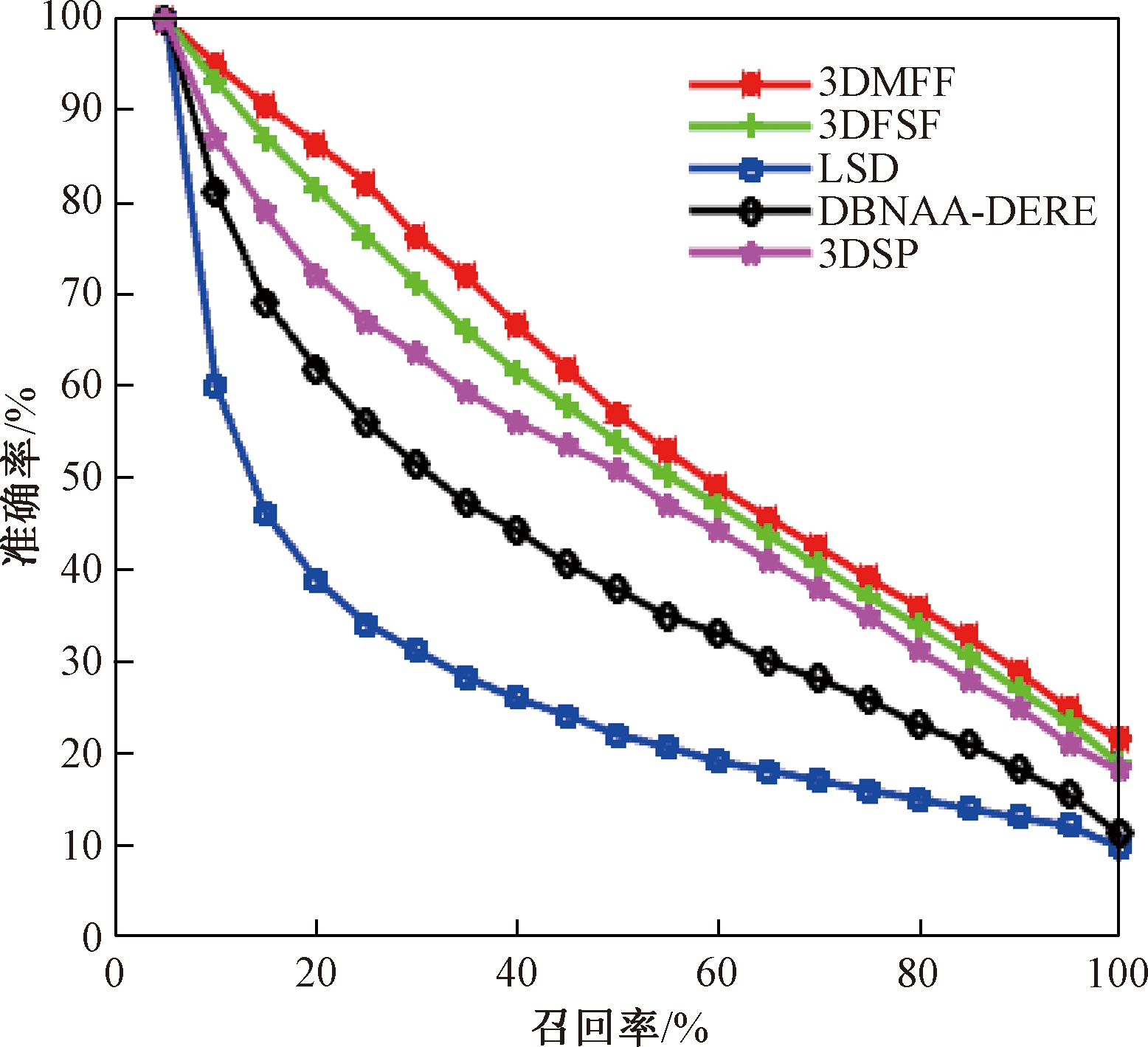
图6 5种检索方法的P-R曲线
Fig.6 P-R curve of five retrieval methods
表2 PSB模型库上的试验对比
Tab.2 Experiment comparison on PSB database %
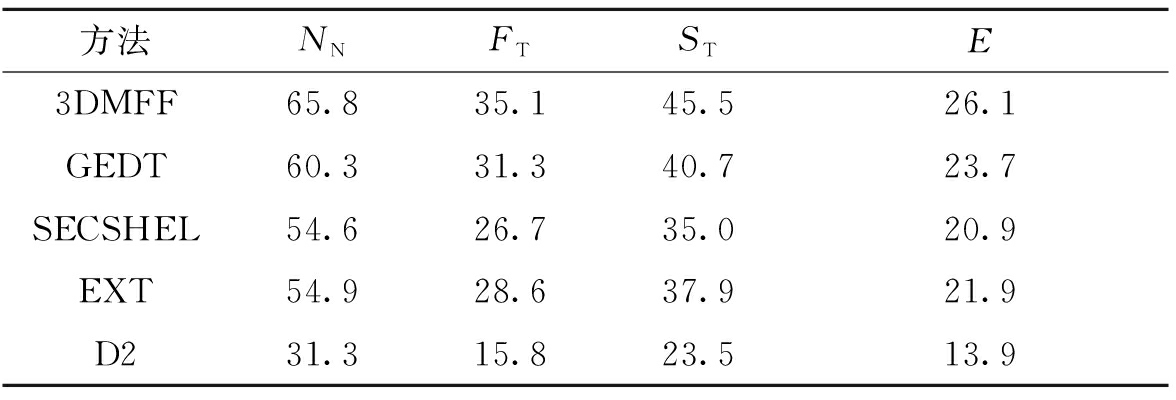
方法NNFTSTE3DMFF65.835.145.526.1GEDT60.331.340.723.7SECSHEL54.626.735.020.9EXT54.928.637.921.9D231.315.823.513.9
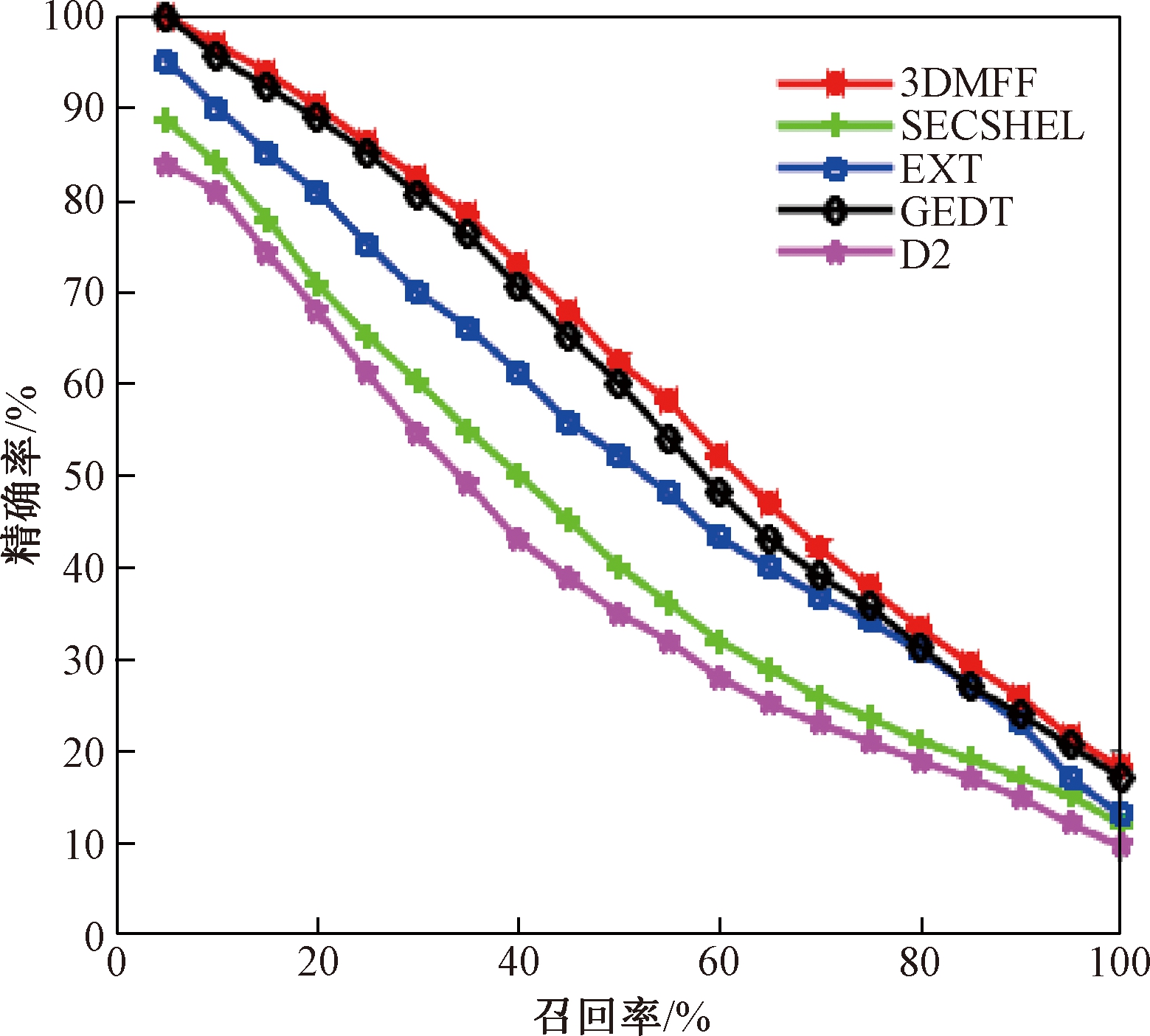
图7 5种检索方法的P-R曲线
Fig.7 P-R curve of five retrieval methods
4 总结
笔者针对现有成果在特征选择、表示和融合方面存在的问题,提出基于多特征融合的三维模型检索方法.在SHREC2012GTB和PSB两个数据库上的对比试验表明,使用该方法检索精度都有提高.但距离加权求和的融合方式不具有通用性且计算复杂,在下一步工作中,考虑将多模态应用于特征融合,将视觉显著性应用到模型提取中,通过深度卷积神经网络进行训练,采用更高效的轮廓提取方式和局部特征,使模型描述更精准全面.
[1] ANKERST M, KASTENMÜLLER G, KRIEGEL H P, et al. 3D shape histograms for similarity search and classification in spatial databases[C]//Advances in Spatial Databases. Berlin Heidelberg:Springer, 1999: 207-226.
[2] PAQUET E, RIOUX M. A content-based search engine for VRML databases[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington D C: IEEE, 1998: 541-546.
[3] OSADA R, FUNKHOUSER T, DOBKIN D. Shape distributions [J]. ACM transactions on graphics, 2002, 21(4): 807-832.
[4] CHEN D, TIAN X, SHEN Y, et al. On visual similarity based 3D model retrieval [J]. Computer graphics forum, 2010, 22(3): 223-232.
[5] VRANIC D V. DESIRE: a composite 3D-shape descriptor[C]//Proceedings of the 2005 IEEE International Conference on Multimedia and Expo.Amsterdam: IEEE, 2005:4.
[6] ZOU K S, IP W H, CHEN Z Q,et al. A novel 3D model retrieval approach using combined shape distribution[J]. Multimedia tools and application, 2014, 69(3):799-818.
[7] LI B, JOHAN H. 3D model retrieval using hybrid features and class information [J]. Multimedia tools and applications, 2013, 62(3): 821-846.
[8] SHILANE P, MIN P, KAZHDAN M, et al. The princeton shape benchmark[C]//Proceedings of Shape Modeling Applications. Genova: IEEE, 2004:167-178.
[9] CANNY J. A computational approach to edge detection[J]. IEEE transactions on pattern analysis and machine intelligence, 1986, 8(6): 679-698.
[10] BELONGIE S,MALIK J, PUZICHA J.Shape matching and object recognition using shape contexts [J]. IEEE transactions on pattern analysis and machine intelligence,2002,24(4):509-522.
[11] 陈实,马天骏,黄万红,等. 基于形状上下文描述子的步态识别[J]. 模式识别与人工智能, 2007, 20(6): 794-799.
[12] KUHN H W. The Hungarian method for the assignment problem [J]. Naval research logistics quarterly, 1955, 2(1): 83-97.
[13] LI B, LU Y J, LI C Y, et al. A comparison of 3D shape retrieval methods based on a large-scale benchmark supporting multi modal queries [J]. Computer vision and image understanding, 2015, 131: 1-27.
[14] LI B, GODIL A A, AONO M, et al. SHREC′12 Track: Generic 3D Shape Retrieval[C]//Proceedings of the 5th Eurographics Conference on 3D Object Retrieval. Cagliari: Computing Machinery, 2012: 119-126.
[15] 徐平安, 唐雁, 陈强,等. 融合细节与整体特征的三维模型检索方法[J]. 西南大学学报(自然科学版), 2015, 37(10): 131-137.
[16] LENG B, DU C, GUO S, et al. A powerful 3D model classification mechanism based on fusing multi-graph [J]. Neurocomputing, 2015, 168: 761-769.
[17] OSADA R, FUNKHOUSER T, CHAZELLE B, et al. Matching 3D models with shape distributions [C]//International Conference on Shape Modelling and Applications. Washington D C: IEEE, 2008:154-166.
[18] KAZHDAN M,FUNKHOUSER T,RUSINKIEWICZ S.Rotation invariant spherical harmonic representation of 3D shap descriptirs[J]. Eurographics symposium on geometry processing, 2003,43: 156-164.
[19] 杨文柱,刘晴,王思乐,等.基于深度卷积神经网络的羽绒图像识别[J]. 郑州大学学报(工学版), 2018,39(2):11-17.
[20] WANG F, PENG J, LI Y. Hypergraph based feature fusion for 3-D object retrieval [J].Neurocomputing, 2015, 151: 612-619.