0 引言
配电网损耗是电力生产中的一个重要技术经济指标,也是县级供电企业节能降损关注的主要问题之一[1-2].配电网的理论线损计算则是线损分析、线损指标管理以及指导节能降损的主要依据.由于线损计算涉及因素较多,计算过程复杂,以均方根电流法和等值电阻法等为代表的传统线损计算方法均进行了大量简化,且均在工频条件下进行计算,部分改进方法中,也主要集中于考虑系统三相不平衡以及大量使用量测数据两个方面,鲜有考虑谐波因素的影响[3-5].
近年来,随着新能源的快速发展及各类新型用电设备的广泛使用,谐波问题对配电网的影响日趋严重.部分商业用电负荷的测试结果显示[6],谐波电流总畸变率多数在15%~30%,个别高达45%,谐波问题引起的附加损耗已成为配电网理论线损计算中不可忽略的部分.鉴于此,笔者在全面分析传统线损计算方法的基础上,采用交流电阻系数和谐波损耗因子来表征谐波环境集肤效应与涡流效应对线路及变压器的影响机理,并结合典型配电变压器与线路,对提出的线损模型量化分析,最后搭建Matlab仿真模型,对该模型进行验证.
1 传统配电网损耗计算方法
根据电力网电能损耗计算导则的介绍,由于配电网线路分支较多,并且一直以来负荷元件(配电变压器、低压负荷等)都不具备测量条件,因此配电网线损计算多采取简化处理,常用的计算方法有如下几种.
(1) 均方根电流法.均方根电流法是理论线损的基本计算方法.设R为配电网中元件电阻,I为流过该元件的电流有效值,在某个周期T内该元件的电能损耗为:
ΔA=3![]() I2Rdt.
I2Rdt.
由于负荷曲线的解析表达式I=f(t)无法准确获取,上式积分难以求取.通常假设每小时内电流值一定,用代表日24 h正点负荷电流的测量值对上式进行分段积分计算.设Ii为代表日24 h正点时刻负荷测量值,则全天24 h元件电阻中的损耗为![]() 定义代表日方均根电流
定义代表日方均根电流![]() 上式可进一步简化为
上式可进一步简化为![]()
(2) 平均电流法与最大电流法.平均电流法与最大电流法都是均方根电流法的改进算法.平均电流法又称为形状系数法,是利用平均电流与均方根电流间的比例关系进行计算.由于用平均电流计算出的损耗偏小,故引入等效系数K=Ijf/Iav,其中Iav为代表日负荷电流的平均值,得到电能损耗![]() 最大电流法,又称为损失因数法,该方法是利用最大电流与均方根电流间的比例关系计算.用最大电流法得到的损耗偏大,故引入损失因数
最大电流法,又称为损失因数法,该方法是利用最大电流与均方根电流间的比例关系计算.用最大电流法得到的损耗偏大,故引入损失因数![]() 进行修正,总电能公式变形为
进行修正,总电能公式变形为![]()
(3) 等值电阻法.等值电阻法是针对低压配电网节点多、分支多、元件多的特点提出的一种简化算法.该算法将线损分为由变压器铁芯产生的不变损耗和变压器绕组及线路电阻随电流变化产生的可变损耗两类.为进一步简化,通过导线和公用配变等值电阻来对可变损耗部分进行计算.
导线的等值电阻表示为:
(1)
式中:∑Sa是该线路各节点配变总容量;Si是经过第i段导线供电的配变总容量;Ri为第i段导线电阻.
配变绕组的等值电阻表示为:
(2)
式中:Pk(j)为第j节点公变的短路损耗值;UN为配电网额定电压.
综上,可得到代表日的总损耗:
(3)
在传统的配电网理论线损计算方法中,由于计算过程粗略,计算结果存在较大误差.此外,传统算法注重对配电网整体损耗的简化分析,对线路中电容器、电抗器、测量装置的损耗均有考虑,涉及范围较广但缺乏对重点损耗元件的深入分析.
2 考虑谐波因素的配电网损耗模型
配电网中由线路和变压器引起的损耗,占总损耗的90%多[6].谐波情况下,由于集肤效应和涡流效应,线路电阻以及变压器绕组增大,引起的附加电能损耗相当可观.因此,笔者主要对线路和变压器的谐波损耗进行探讨.
2.1 谐波背景下线路损耗计算模型
线路的损耗与线路电阻和流过线路的电流有关.理想情况下,线路电阻为一定值,可由I2R直接求取.谐波背景下线路损耗的计算,则必须将各次谐波电流Ih和谐波电阻Rh考虑在内.故由叠加原理可知,考虑谐波影响的线路损耗可表示为:
(4)
谐波电流Ih可由电流表测量值经傅里叶展开得到.谐波电阻Rh是频率f的函数,主要受集肤效应和邻近效应影响,计算相对复杂.
Morgan经过大量的对比试验,忽略钢芯导电性给出了钢芯铝绞线的近似模型.不同频率下相对电阻增量定义如下[7]:
ΔR/R=Y(1-φ)-1/2-1,
(5)
其中,Y=1+a(z)[1-β/2-β2b(z)],
φ![]()
β=2t/d,z=8π2t2fγ;γ=10-9/πtR(d-t),t为铝层厚度,d为钢芯铝绞线直径,R为单位长度的直流电阻值.该方法计算较为精确,但由于所需参数多,计算过程复杂,不适用于工程中的近似计算.
文献[8]以架空钢芯铝绞线为对象,通过对电流密度积分求出电流和焦耳热功率.考虑在低压线路导线以阻性为主,热功率近似等于电阻功率,消去中间变量电流,得到不同频率下谐波电阻公式:
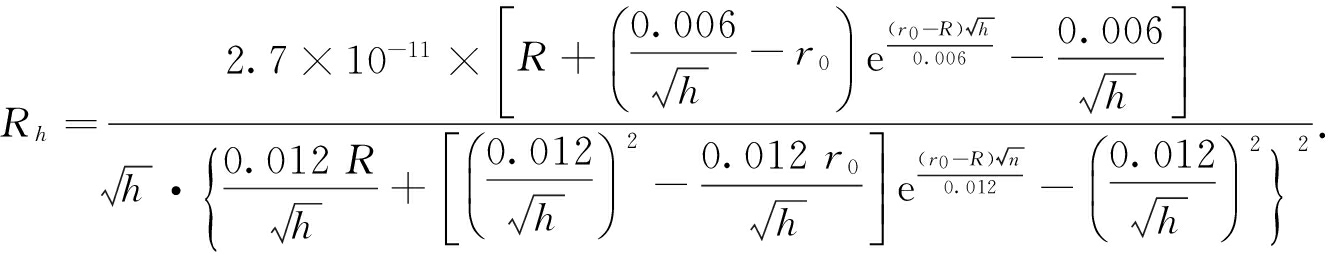
(6)
但由该式计算的谐波电阻在20次以上的工频谐波环境下才有明显变化,不适用于线路中常见的5、7、11、13、17、19等低频次谐波.
日本学者通过对导线的交直流电阻测试,引入交直流电阻系数k=RAC/RDC来表征不同频率下交直流电阻比[9],该方法不但考虑了导线的集肤效应,而且考虑了钢芯的磁滞和涡流导致的铁损.其中集肤效应系数k1计算公式如下:
k1= 0.996 09+0.018 578 x-0.030 263 x2+
0.020 735 x3.
(7)
其中单一绞合线(铝合金线、铝合金芯铝绞线)和复合绞合线(铝线+钢线)情况下,x分别按式(8)和(9)取值.
![]() ;
;
(8)
(9)
式中:f为频率,Hz;D1为绞线的外径,mm;D2为钢线的外径,mm.
对单一绞线及复合绞线(铝线层数为偶数),铁损效应系数k2=1,复合绞线(铝线层数为1以上奇数)时:
k2= 0.999 47+0.028 859 y-0.005 934 8y2+
0.000 422 59y3,
(10)
式中:y=I/A,I为绞线电流,A,A为铝线截面积,mm2.
通过上式得出的k1、k2的值小于1时,取k1=1,k2=1.k1k2即为求得的导线交直流电阻比.该法考虑因素全面且计算相对简单,更适合谐波背景下的交流电阻计算.
2.2 谐波背景下变压器损耗计算模型
变压器损耗包含空载和负载损耗.空载损耗又称铁耗,主要包括磁滞和涡流损耗,与负载无关;负载损耗又称铜损,由绕组的直流损耗、绕组涡流损耗和杂散损耗构成.系统含有谐波时,铁耗会受谐波电压的影响,铜耗受谐波电流的影响.
(1) 空载损耗的分析与计算.磁滞损耗是由铁磁材料的磁滞现象产生,与最大磁密Bm的平方成正比.由于磁化过程需要交变的磁场,所以其大小还受频率f影响[10].总的来说磁滞损耗PH可表示为:
(11)
式中:C1由硅钢片材料性质决定,为常数;V表示铁磁材料体积.当含有多次谐波时,谐波电压含量越高,磁滞损耗则越大,可表示为:
PH=P1+P2+P3+...+Ph=![]() S.
S.
(12)
式中:Ph为第h次谐波的磁滞损耗;Uh为第h次谐波电压;U1为基波电压;φh为h次谐波电压初相角.
谐波背景下的涡流损耗也将随谐波电压含量的增大而增大,其计算式为:
Pw=P1+P2+P3+...+Ph=1+![]() 2Ceh,
2Ceh,
(13)
Ceh由电磁波的透入深度决定,Ceh的表达式如下:
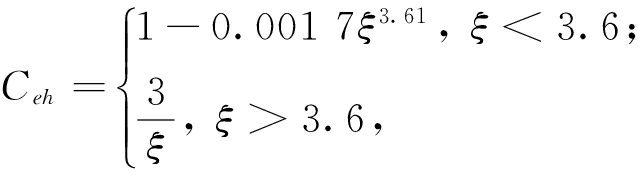
(14)
其中,
(15)
式中:Pw为涡流损耗;Uh为第h次谐波电压;U1为基波电压;c为铁芯厚度;u为铁芯滲透性;γ为铁芯电导率;f为基波频率.
综上可知,变压器空载附加损耗主要取决于电压.由于无功补偿与滤波装置的大量投入,通常情况下系统谐波电压THD不超过5%;并且各谐波分量幅值很小,一般在基波幅值的2%~3%以下[11-12],因此,这部分损耗可忽略.
(2)负载损耗的分析与计算.变压器的负载损耗PLL包括电阻损耗P(I2R)和总杂散损耗PTSL.尽管总杂散损耗实质上都是由漏磁引起的涡流损耗,又可根据其分布位置不同,分为在绕组线圈内引起的绕组涡流损耗PEC和在铁芯、夹件、油箱等部位导致的其他杂散损耗POSL,故变压器负载损耗表示为:
PLL=P+PTSL=P+PEC+POSL.
(16)
目前变压器绕组采用的交流电阻模型多为![]() 简单的将交流电阻这样等效,忽略了集肤效应与邻近效应的影响,在线路存在高次谐波时,存在较大误差[13-14].IEEE Std C57.110通过引入谐波损耗因子,给出了谐波情况下根据测试数据计算负载损耗的方法[15]:
简单的将交流电阻这样等效,忽略了集肤效应与邻近效应的影响,在线路存在高次谐波时,存在较大误差[13-14].IEEE Std C57.110通过引入谐波损耗因子,给出了谐波情况下根据测试数据计算负载损耗的方法[15]:
PLL=PO+FHL-ECPEC-O+FHL-OSLPOSL-O,
(17)
其中,FHL-EC,FHL-OSL为绕组涡流谐波因子与其他杂散损耗谐波因子,定义式如下:
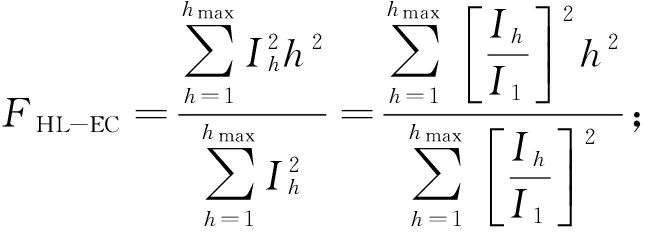
(18)
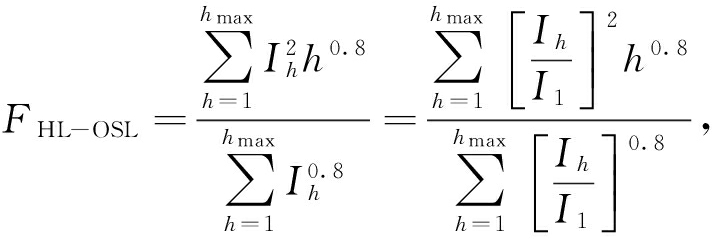
(19)
式中:h为谐波阶次;I1为基波电流;Ih为第h次谐波电流.
PO,PEC-O,POSL-O为工频实测电流的各部分损耗,需通过额定损耗值乘以修正因子![]() 2求得.由于工程中谐波分析装置所测结果多为各次谐波含有率(各次谐波电流与基波电流之比),故作如下转换:
2求得.由于工程中谐波分析装置所测结果多为各次谐波含有率(各次谐波电流与基波电流之比),故作如下转换:
(20)
当以额定正弦电压供电时,变压器总负载损耗的表达式如下:
PLL-R=PR+PEC-R+POSL-R,
(21)
式中:PLL-R为额定负载损耗(即短路实验损耗);PR为额定电阻损耗,可由式(21)求得:
(22)
式中:K根据变压器相数选取,单相取1,三相取1.5.原副边的直流电阻可由实验测试报告获取.
额定涡流损耗PEC-R与额定其他杂散损耗POSL-R占总杂散损耗的比例基本固定,标准根据大量测试报告给出了二者的比例系数.对于油浸式变压器二者占总杂散损耗的比例分别为33%和67%,干式变压器刚好相反.综上分析,谐波背景下变压器总损耗可表示为:
PT= PNL+(PR+FHL-ECPEC-R+FHL-OSLPOSL-R)·
(I/IR)2.
(23)
3 考虑谐波因素的损耗量化分析
根据上文给出的线路与变压器的谐波线损模型,分别选取交流电阻系数法及谐波损耗因子法来计算线路谐波损耗及变压器的谐波铜耗.在考虑谐波因素的配电网损耗计算中,谐波电流起主导作用,故通过实例量化分析不同电流谐波含有率,不同谐波次数对线路以及变压器损耗的影响机理.其中线路采用标称截面积为120 mm2的JLHA2铝合金绞线,直流电阻RDC=0.287 7 Ω/km,电抗X=0.335 Ω/km,线路长度20 km.选用S11-50/10型变压器,连接组标号为Dyn11.线路5、7、11、13、17、19次谐波电阻分别为5.894、6.024、6.386、6.612、7.144、7.446.变压器参数如表1所示.
在谐波电流含有率为1%、5%、7%、11%、13%、17%、19%的情况下,分别对5、7、11、13、17、19次谐波损耗进行计算,其中线路基波电流值选择变压器一次侧额定电流,变压器所用基波电流选用二次侧额定电流.根据计算结果,拟合出“损耗-谐波电流含有率”和“损耗-谐波次数”曲线,如图1~2所示.同时,考虑谐波与不考虑谐波时,对线路及变压器的损耗进行对比,如图3所示.
表1 变压器参数
Tab.1 Parameters of transformer
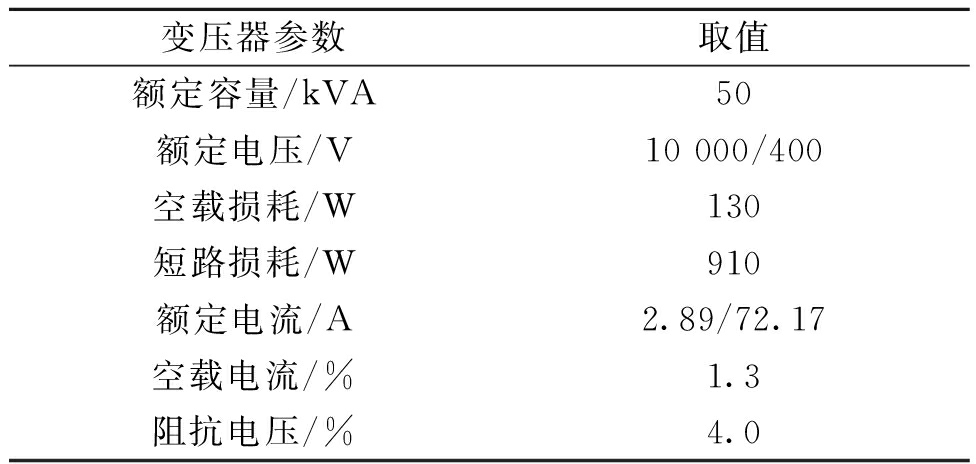
变压器参数取值额定容量/kVA50额定电压/V10000/400空载损耗/W130短路损耗/W910额定电流/A2.89/72.17空载电流/%1.3阻抗电压/%4.0
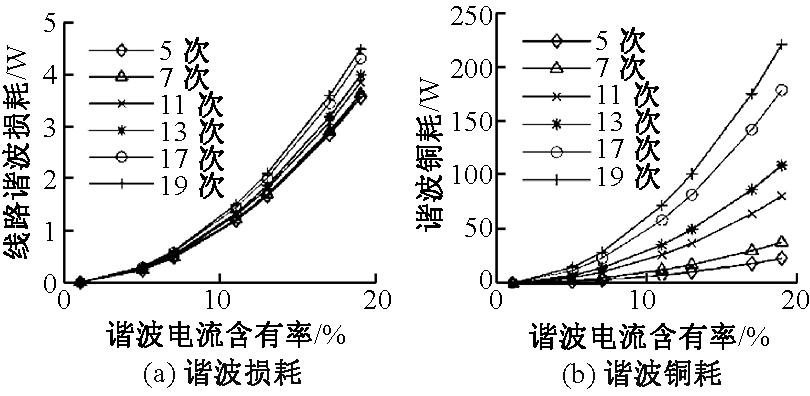
图1 5~19次谐波损耗随谐波电流含有率变化
Fig.1 Variation of 5~19 harmonic loss with harmonic current ratio

图2 不同谐波电流含有率谐波损耗随谐波次数变化曲线
Fig.2 Variation of harmonic loss with harmonic orderunder different harmonic current ratio
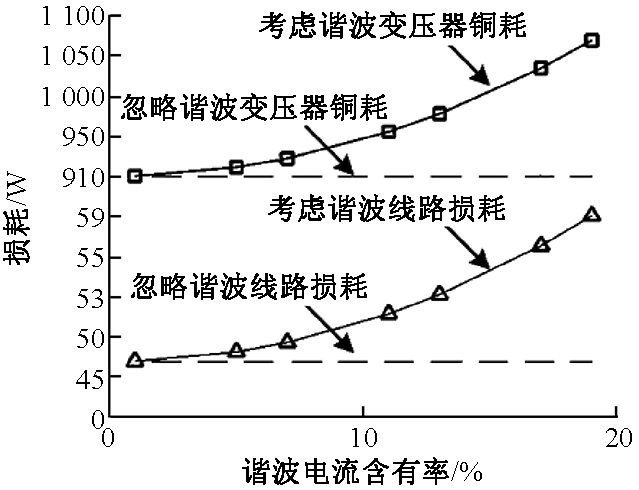
图3 考虑或忽略谐波情况下损耗变化情况
Fig.3 Variation of lossunder considering or ignoring harmonic factor
由上述分析知:考虑谐波因素后,变压器及线路损耗均有不同程度增加,当谐波电流含量达到19%时,线路和变压器损耗分别增加约23.2%和18.7%.谐波次数一定时,线路谐波损耗与谐波电流含有率的平方成正比,变压器较高次谐波与谐波电流含有率的平方近似成正比.谐波含有率一定,线路与变压器谐波损耗均随谐波次数增大而增大.线路谐波损耗主要受交流电阻系数影响,变化平缓;变压器谐波损耗主要受谐波损耗因子影响,变化较快.
4 仿真验证
4.1 仿真建模
为了验证上文量化分析结果,首先在Matlab/simulink中,对系统中含量较高的5、7、13次谐波在不同谐波含有率下进行单独仿真,并分析其与计算结果的误差.首先采用三相可编程电压源,模拟不同谐波次数、不同谐波含量的注入,所选输电线路与变压器型号与上文量化计算一致,换算后仿真参数设置如下:线路电阻5.76 Ω、电感0.021 4 H;变压器一次电阻18.2 Ω、二次电阻0.029 Ω、一次电感0.127 H、二次电感0.204 mH、激磁电阻769 230 Ω、激磁电感0.127 H.
模拟实际系统中多次谐波共同存在的情况,对总体配网损耗仿真.由于三相可编程电源产生谐波的数量有限,改用负荷侧并联整流装置,向系统注入谐波,仿真模型如图4所示.其中,黑色矩形模块为三相电压电流测量装置,通过改变两个电能表的接入位置来完成对线路及变压器谐波功率损耗的单独或混合测量.整流元件由同步六脉冲发生器触发,电能表由三相瞬时功率测量元件和积分环节构成.选用连续型仿真模型ode23tb求解算法,仿真时间设置为0.4 s.整流部分负载电阻R=13 Ω,滤波电感L=1 mH,电容C=3 300 μF,有功负荷P=20 kW,感性无功QL=4 kW·h,其他参数与上文单独仿真一致.
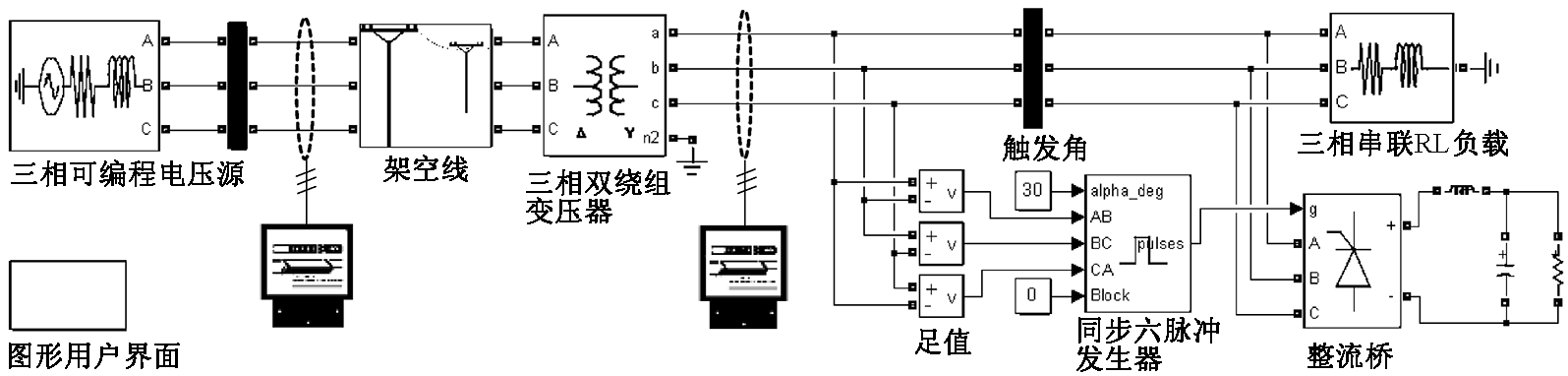
图4 线损仿真模型
Fig.4 Simulation model of line loss
4.2 实例分析
(1)单次谐波影响.仿真结果及不同含有率仿真与计算误差值如图5~6所示.
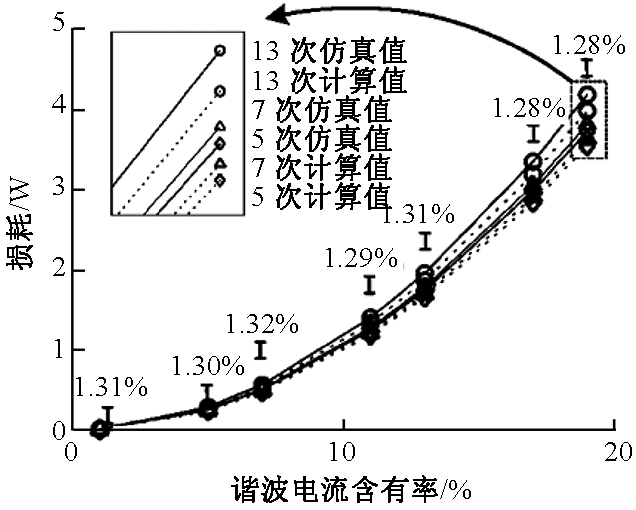
图5 线路谐波损耗仿真与计算结果对比
Fig.5 Comparison of simulation and calculation results of harmonic line loss
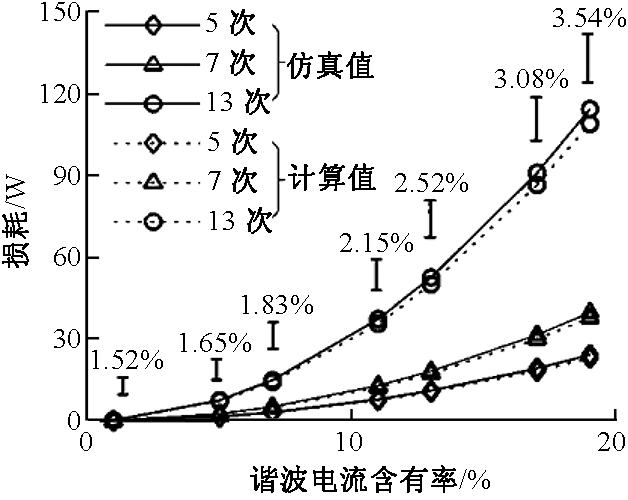
图6 谐波铜耗仿真与计算结果对比
Fig.6 Comparison of simulation and calculation results of harmonic copper loss
由图可知,总体来看,线路及变压器仿真结果与量化计算结果较为接近,且仿真值略大于计算值.由于线路模型与实际情况相比仍然存在一些差异,线路计算结果与仿真值始终存在误差,但误差变化不大,基本稳定在1.3%附近,满足工程计算要求.变压器计算误差随谐波含量的增加有所增大,但总体不超过4%.究其原因为笔者所采用的计算模型忽略了附加铁耗的影响,而仿真过程中,表计测量的损耗包含谐波引起的附加铁耗.由前文分析知,铁耗会随谐波电压含有率的增大而增大.实际中,谐波电压一般满足国标要求,可忽略这部分损耗.
(2)混合谐波影响.仿真过程中,测得变压器一二次侧电流有效值分别为2.42 A和60.52 A,线路出口处电表有功电量为16 730 W,两表抄见电量之差为540 W.根据变压器一二次侧电压电流测量结果,使用FFT分析工具,进行谐波分析.分析得到,系统谐波以5、7、11、13、17、19次为主;一次电压总谐波畸变率为0.08%左右,负荷侧为4.64%左右,均在5%以下,满足所在电压等级国标限制.各次谐波电流含有率如表2所示.
表2 谐波电流含有率
Tab.2 Harmonic current ratio

h一次HRI/%二次HRI/%525.2625.90712.1012.41113.173.25133.453.54170.850.87191.531.57
注:HRI为谐波电流含有率.
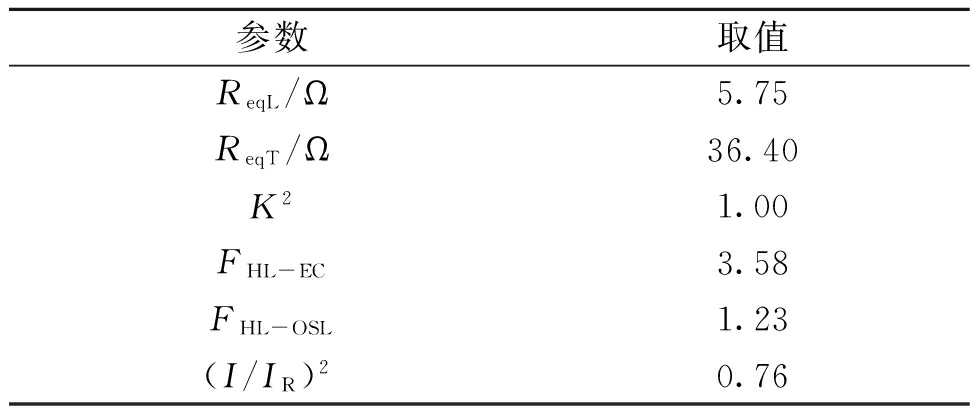
为了与传统线损计算方法对比,根据上述测量数据,同时用等值电阻法计算.由于仿真线路简单,仿真过程处于稳态,式(3)中平均电流Iav近似取为基波电流有效值.根据式(18)计算变压器谐波损耗因子等参数,结果如表3所示.利用以上数据及表1相关参数,根据式(7)、(10)、(22)进行线路及变压器的损耗计算,得到电能损耗与线损率计算结果如表4所示.由结果可知:传统等值电阻法,忽略了谐波因素,计算结果误差较大; 笔者给出的考虑谐波因素的理论线损计算方法,与仿真结果更为接近.
表3 变压器相关参数值
Tab.3 Transformer related value
参数取值ReqL/Ω5.75ReqT/Ω36.40K21.00FHL-EC3.58FHL-OSL1.23(I/IR)20.76
表4 线损计算结果
Tab.4 Calculation results of line loss
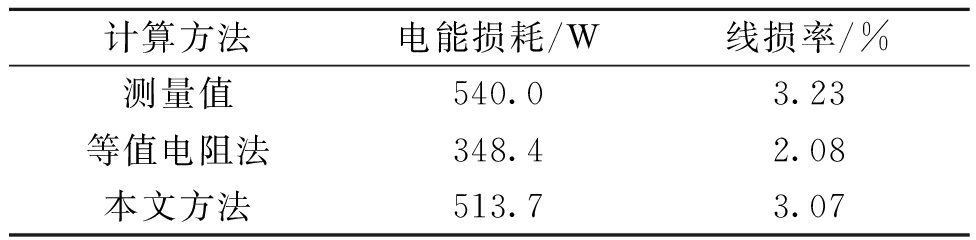
计算方法电能损耗/W线损率/%测量值540.03.23等值电阻法348.42.08本文方法513.73.07
5 结论
(1)笔者提出的考虑谐波因素的配电网理论线损计算方法,能充分反映谐波对线路、变压器带来的附加损耗.虽然求解过程复杂程度有所增加,但与传统等值电阻法相比,提高了计算结果的精确度,对降损工作更具指导意义.
(2)笔者只单一考虑了电能质量问题中的谐波问题.配电网三相负荷不平衡,电压偏差以及复合电能质量因素作用下给系统带来的附加损耗,仍需要进一步研究.此外如果加入实际线路测量结果,与仿真以及计算结果三者对比分析,将进一步验证该方法的有效性.
(3)计算结果表明变压器铜耗与输电线路损耗均随谐波电流含量及谐波次数的增大而增大,且铜耗占据的比重远大于线路损耗和变压器铁耗,因此限制变压器谐波电流的大小和次数对于减小总线损具有重要意义.
参考文献:
[1] 杨文锋,王彬宇,程卓,等. 城市中低压配电网降损规划决策方法[J]. 电网技术,2014,38(9):2598-2604.
[2] 赵国生,詹天乐,李博. 计及线路损耗的峰谷分时电价优化模型[J]. 郑州大学学报(工学版), 2017,38(6):45-49.
[3] 徐长宝,李怀宇,冯成,等. 电力系统三相不平衡附加损耗的分配[J]. 水电能源科学,2016,34(8):189-193.
[4] 李滨,杜孟远,韦维,等. 基于准实时数据的智能配电网理论线损计算[J]. 电力自动化设备,2014,34(11): 122-128.
[5] 赵磊,栾文鹏,王倩. 应用AMI数据的低压配电网精确线损分析[J]. 电网技术,2015,39(11):3189-3194.
[6] 李博. 低压配电网谐波对网损的影响及对策研究[D]. 淄博:山东理工大学电气与电子工程学院, 2015.
[7] MORGAN V T, FINDLAY R D, DERRAH S. New formula to calculate the skin effect inisolated tubular conductors at low frequencies[J]. IEE proceedings-science,measurement technology,2000,147(4): 169-171.
[8] JIANG L M, YAN H G,MENG J X,et al. Harmonic loss quantitative model of transmission line considering the skineffect[C] //2016 IEEE International Conference on Power and Renewable Energy (ICPRE). Shanghai:IEEE Press,2016: 19-23.
[9] 张瑞永,赵新宇,陶礼学. 架空导线的交流电阻计算方法对比[J] .电线电缆,2014,4(4): 1-4.
[10] 张占龙,王科,李德文,等. 变压器谐波损耗计算及影响因素分析[J]. 电力系统保护与控制, 2011, 39(4): 68-72, 78.
[11] 刘书铭,施红,冯蕾. 考虑集肤效应与邻近效应的变压器谐波损耗模型[J]. 电力自动化设备, 2015, 35(3): 133-139.
[12] SADATISB, TAHANIA,DARVISHIB,et al. Comparison of Distribution Transformer Lossesand Capacity under Linear and Harmonic Loads[C] //2nd IEEE international conference on power and energy. Johor Baharu,Malaysia: IEEE, 2008, 1265-1269.
[13] 李琼林,邹磊,刘会金,等. 电力变压器谐波损耗仿真计算与实验研究[J]. 电网技术, 2013, 37(12): 3521-3527.
[14] 夏焰坤. 电气化铁路单三相组合式变压器电气特性分析[J]. 郑州大学学报(工学版), 2016, 37(4): 11-14,35.
[15] IEEE Recommended Practice for Establishing Liquid-Filled and Dry-Type Power and Distribution Transformer Capability When Supplying Nonsinusoidal LoadCurrents:IEEE Std C57.110—2008[S].