0 引言
目前对大型机械设备传动系统的动力学特性分析研究，主要是在确定性的框架内进行的，很少考虑系统中存在的不确定性因素，如齿轮啮合、联轴器接触状态等，对传动系统有限元模型动态特性分析造成的影响，使仿真结果不能有较好的工业应用[1].因此，提高有限元模型的精度使其能准确反映系统动力学特性，对机械设备传动系统设计及动态特性分析具有重要意义.
近十年来，以分层思想为核心，通过修正子结构有限元模型获得整体结构准确模型的分层修正方法正在迅速发展.针对复杂的机械设备，该方法首先将其分解成简单的子结构，通过统计意义下的模型修正方法识别子结构中的不确定性参数，获得精确的子结构模型，不需做整机实验，由子结构响应不确定性推断出整体结构响应误差的置信度[2].因此，建立精确的子结构有限元模型是分层修正方法解决复杂结构有限元模型响应预测置信度问题的关键.
为探讨复杂大型磨机传动系统的子结构建模方法，采用基于响应面的有限元模型修正技术，以子结构的试验模态频率数据为目标，通过识别模型中的不确定性参数，实现对子结构模型的修正，并进行振型相关性分析及频响曲线对比分析，结果表明修正后的有限元模型精度得到明显提高.
1 基于响应面的有限元模型修正理论
基于响应面的模型修正方法是近年来基于统计分析技术的模型修正方法的研究方向[3-6]，其以显式的响应面模型逼近特征量与设计参数间复杂的隐式函数关系，可以更好地解决传动系统中存在的不确定性参数这一问题，同时修正过程运行快、效率高.
响应面法是以方差分析、回归分析[7]两大数理统计理论技术为基础的一项理论,其主要内容包括：试验设计、参数筛选、响应面拟合及参数修正.
方差分析以筛选显著性参数为目的，其基本思想是计算出各设计参数的离差平方和，然后求得各设计参数和误差的F值，应用F值检验法进行假设检验，找出显著性参数.假设对有限元模型的某一因素X进行F检验，统计量为：
(1)
式中：SX、fX为因素的离差平方和及自由度；SE、fE为误差的离差平方和及自由度.
对于给定的显著水平α，方差比率F检验的准则为：若F≥F1-α(fX,fE)，则认为因素X为显著性参数；反之不显著.
采用回归分析方法以系统特征量y为因变量，设计参数xi(i=1,2,…,k)为自变量，则含交互项的二次多项式响应面模型为：
(2)
式中：
而
分别为设计参数xi的取值范围的上下限；β0、βij、βi、βii为待定系数.其确定方法为：为便于数量级的统一，通过离差标准化方法对设计参数进行线性变换，取得设计参数的归一化数值空间；通过试验设计，将确定的样本点(自变量)代入有限元模型仿真分析得到样本值(因变量)；在样本数据组数大于待定系数个数的前提下，将各组样本数据代入式(2)，通过最小二乘法估计系数β的值.
为保证拟合响应面能够准确描述因、自变量间的关系，需对其进行精度检验.若符合要求则进行模型修正；若不满足则需重新计算.响应面的精度检验依照以下公式：
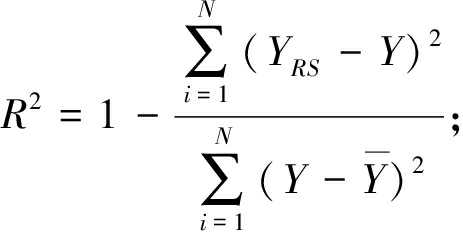
(3)
(4)
式中：N为样本数据的个数；YRS为响应面值；Y为有限元模型分析值；
为其均值；R2表示响应面模型与有限元模型之间的差异程度，取0～1，值越大，二者差异越小.RMSE值与R2值情况相反[8].
模型修正[9-10]可以归结为以下优化问题：
(5)
st.VLB≤p≤VUB,
式中：p为设计参数；{fA(p)}，{fE}分别为试验与仿真的特征值；‖R(p)‖2为特征值残差的2-范数；VLB、VUB为设计空间的上下限.
2 有限元模型建立及模态分析
2.1 小型传动系统装置的设计
以图1所示的7.9 m磨机两级齿轮结构传动系统作为原生系统，基于齿轮传动系统的相似设计理论[11]设计小型传动系统的实验装置.该磨机传动系统为串联式的二级齿轮传动系统.
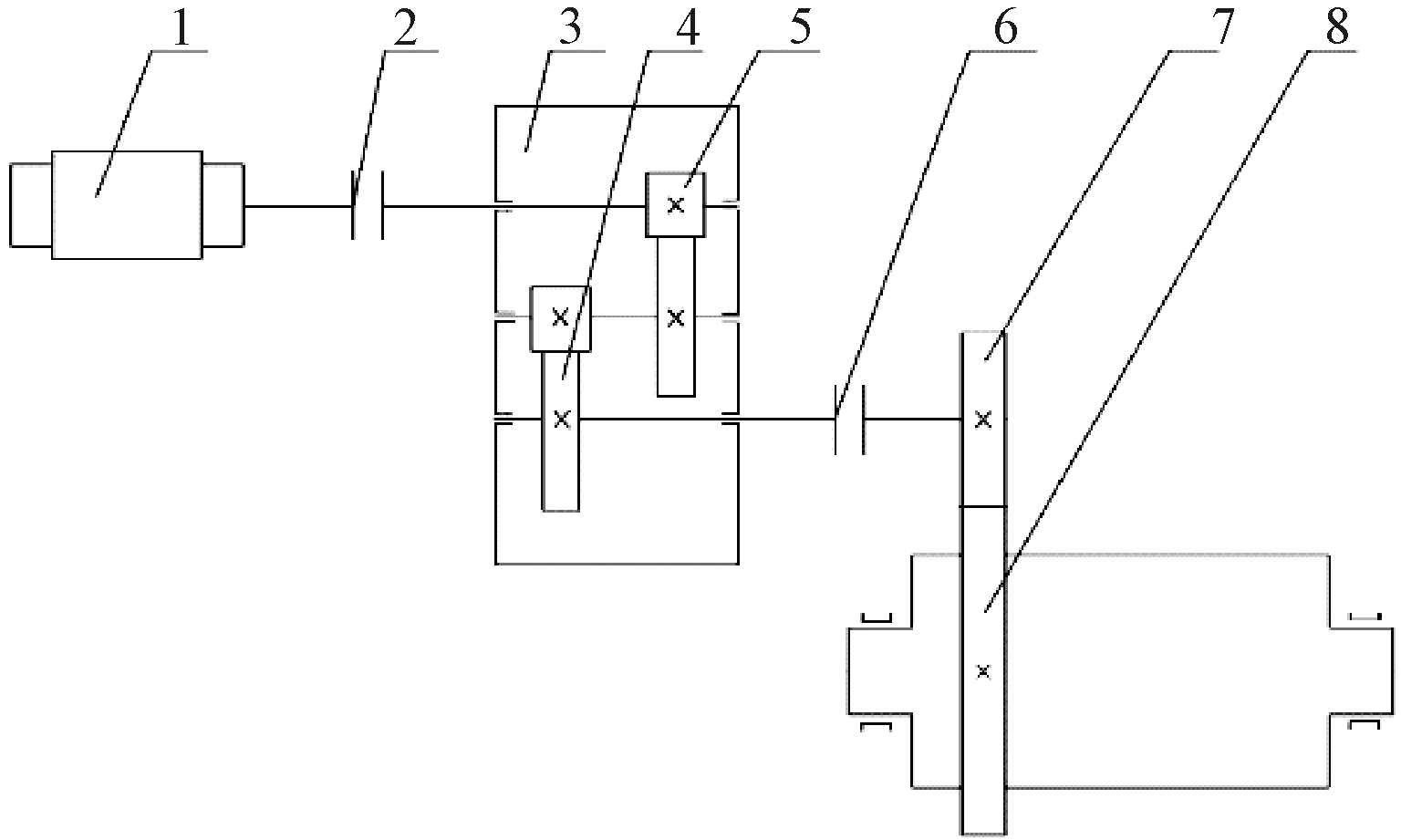
1.电机,2.联轴器,3.减速器,4.低速级齿轮传动,5.高速级齿轮传动,6.联轴器,7.小齿轮,8.负载(包括磨机筒体、大齿轮及载荷)
图1 某7.9 m磨机传动系统简图
Fig.1 Sketch of drive system of a 7.9 meter mill
基于相似系统设计理论[12]，对原生系统的组成要素进行识别，采用相同功能、作用的组成要素，并按照与原生系统一致的顺序进行排序，最终得到结构和功能上与原生系统相似的相似系统.
由于大型机械传动系统一般只关注低阶模态频率，其频率大都在几十到几百赫兹，而尺寸上大幅缩小的小型传动系统，其低阶模态频率极有可能增大至上千赫兹.为满足相似系统在模态频率方面与原生系统的相似性需求，通过在轴上增添圆盘从而增加系统质量的方法降低系统模态频率，保证相似系统前三阶模态频率在200 Hz以内.最终得到小型传动系统的设计方案并成功搭建，如图2所示.
图2 小型传动系统实验台
Fig.2 Small transmission system test bed
2.2 模型建立及模态分析
针对图2所示传动系统，按照传动轴的分布将其分为4个子结构，从左至右依次为子结构A、B、C、D，每个子结构包含传动轴及轴上零件.
在Patran中建立子结构A的有限元模型如图3所示.其中，圆盘通过胀紧套固定在轴上，由于胀紧套内部结构复杂，将其简化为实心圆环块；传动轴、圆盘、胀紧套接触位置单元为柔性接触体单元，采用粘接接触(glue)；轴承采用Bush单元及多点约束MPC方法进行模拟.由于胀紧套替代结构材料未知，暂选为普通碳钢，其余部件材料为普通碳钢，弹性模量E=2.1e11 Pa，泊松比μ=0.3，密度ρ=7 800 kg/m3.对子结构A及圆盘进行模态分析，其前两阶模态如表1所示.
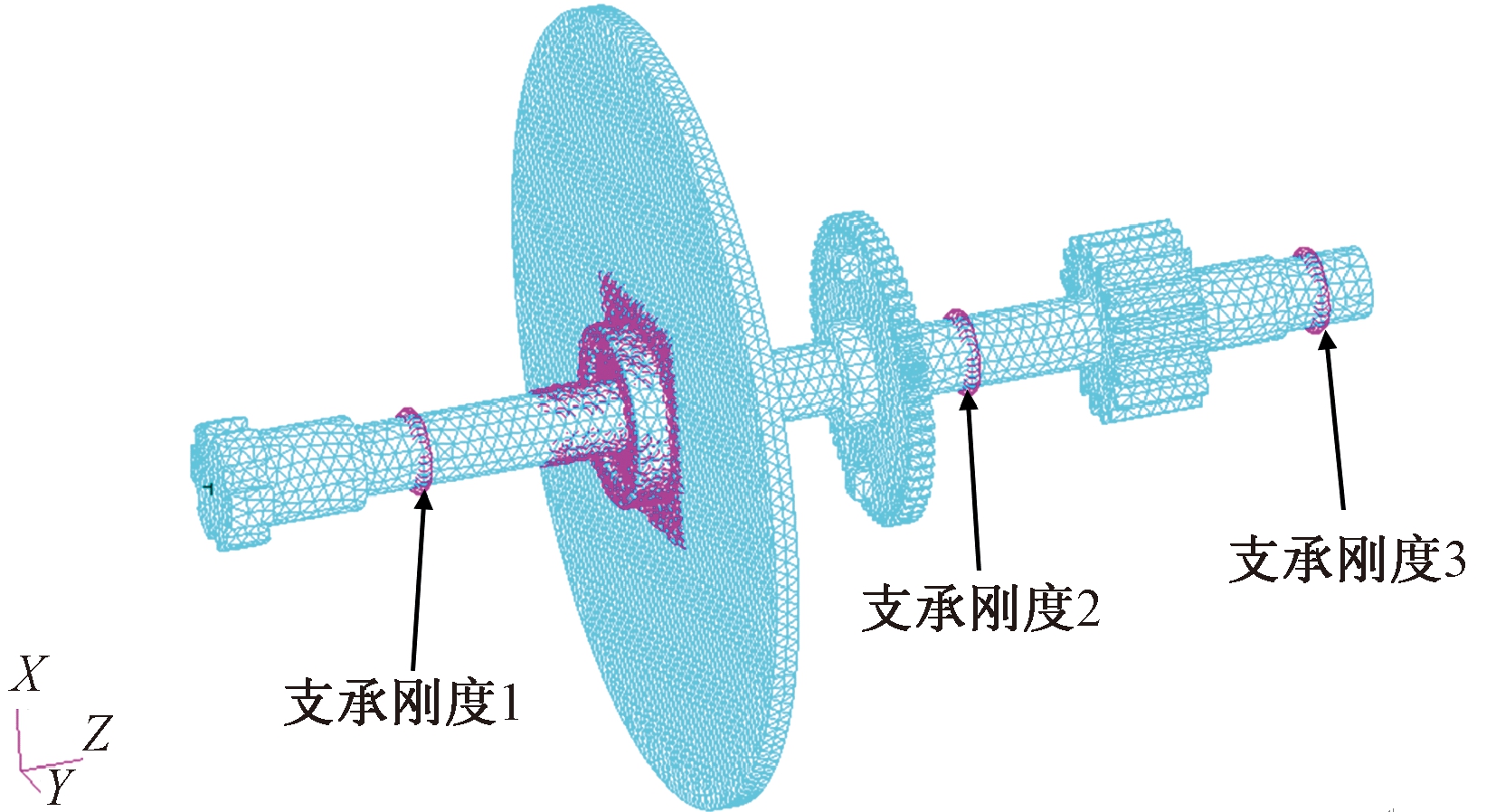
图3 子结构A的有限元模型
Fig.3 Finite element model of substructure A
表1 模态分析结果和试验结果
Tab.1 Modal analysis results and test results
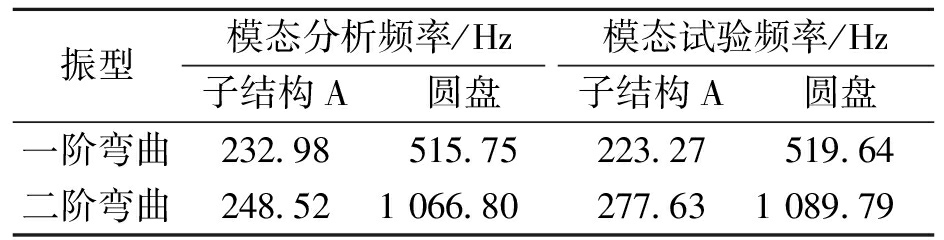
振型模态分析频率/Hz模态试验频率/Hz子结构A圆盘子结构A圆盘一阶弯曲232.98515.75223.27519.64二阶弯曲248.521 066.80277.631 089.79
3 模态试验
试验模态辨识方法有：单点激励单点响应(SISO)、多点激励多点响应(MIMO)、单点激励多点响应(SIMO)以及多参考点锤击法(MRIT)等.其中，MRIT方法能够避免因仅使用一个参考点导致模态丢失的情况，从而最大程度上识别系统所有模态，因此选用MRIT方法进行模态试验，具体方案如下：
(1)试验测点设计，如图4所示，共有被测节点22个.
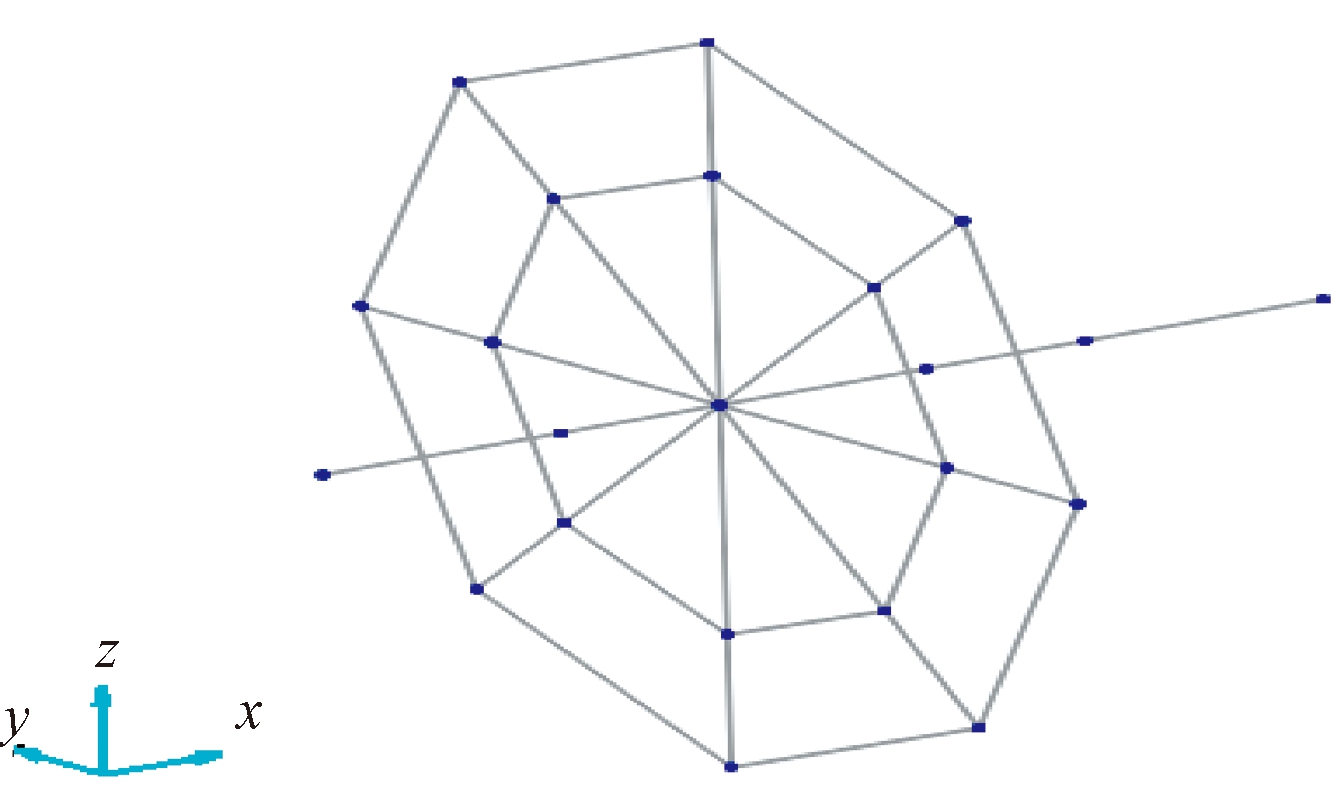
图4 试验模型布点图
Fig.4 Point map of experimental model
(2)数据采集，每个节点测量其三方向的加速度信号.
(3)模态识别，利用N-modal模态识别软件对测试数据进行处理，最终识别出其一阶、二阶模态试验结果，如表1所示.
4 模型修正
4.1 参数的修正
研究中发现，胀紧套替代结构的弹性模量不仅显著影响圆盘模态频率，也影响轴的弯曲模态频率，而轴承支承刚度影响轴弯曲模态频率.因此将胀紧套替代结构弹性模量和轴承支承刚度作为待修正参数.
针对胀紧套替代结构弹性模量，以圆盘的一阶弯曲模态试验数据为目标值，采用响应面法对其进行参数修正.待修正参数只有弹性模量值，因此显著性参数无需筛选，即为弹性模量；采用均匀试验设计方法在有限元模型中分析计算得到样本数据；选取样本数据，以圆盘模态频率为因变量，弹性模量为自变量，拟合二次多项式响应面模型，精度检验结果R2值为0.999 8、RMSE值为2.24e-5，表明响应面精度较高；采用MATLAB软件修正响应面模型，修正过程弹性模量值相对改变量的变化曲线如图5所示.
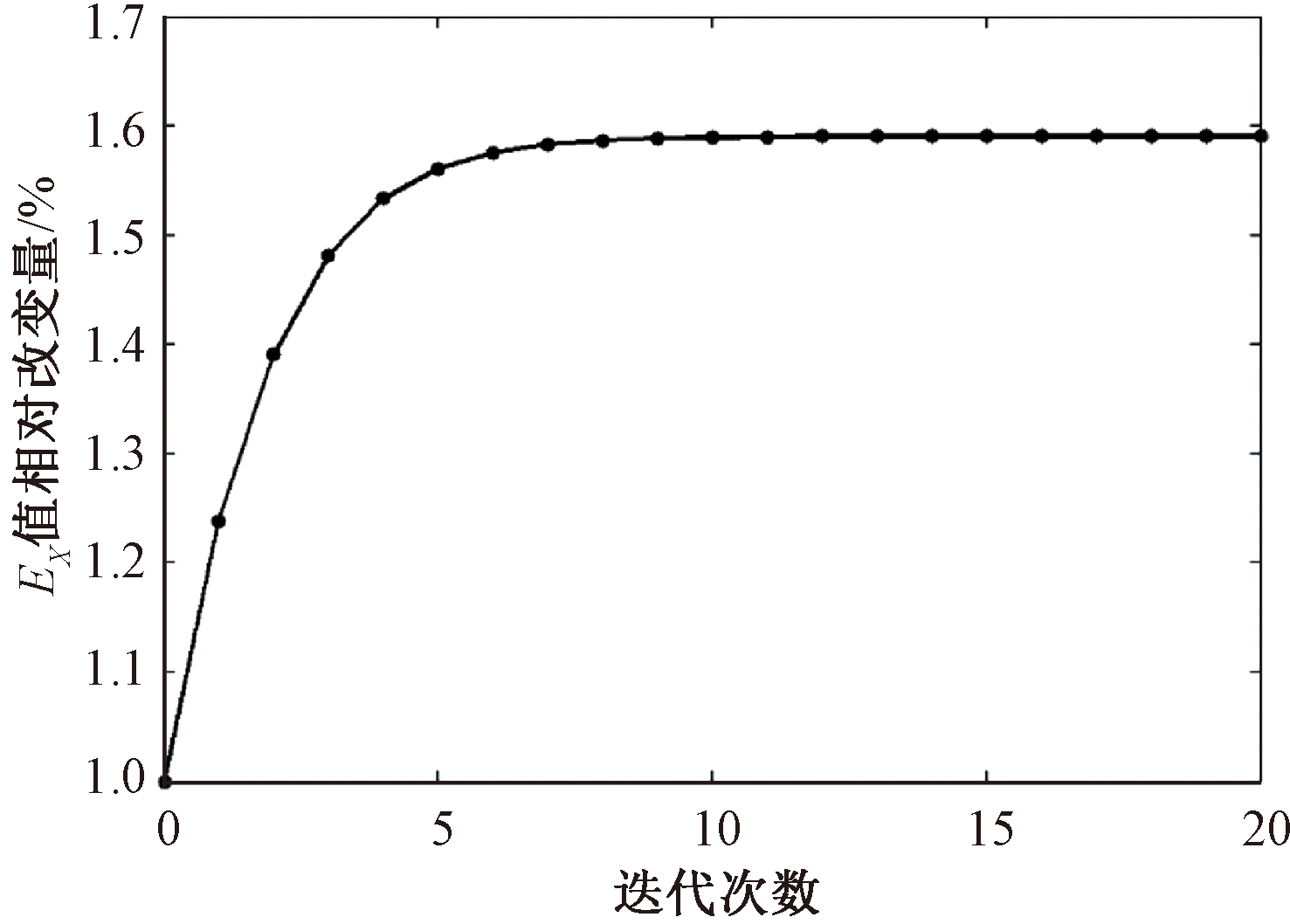
图5 弹性模量值相对改变量变化曲线
Fig.5 Relative change curve of elasticity modulus
修正后弹性模量值为334 090 MPa.对修正后的模型进行计算分析，结果如表2所示，可以看出修正后的模态频率与试验值非常接近，表明模型的修正效果良好.
表2 修正前后模态频率
Tab.2 Modal frequency before and after correction Hz
模态频率试验值修正前模态频率修正后模态频率519.64515.75519.61
针对轴承支承刚度1、支承刚度2、支承刚度3，以正交试验设计方法为基础，在参数的设计空间内确定样本点，代入有限元模型中分析计算得出样本值；对确定的各组样本数据进行方差分析，得到各阶模态的显著性参数，筛选结果见表3.选取样本数据，以子结构A前两阶模态频率为因变量，以各自对应的显著性参数为自变量，拟合响应面模型，响应面模型精度检验结果见表4，R2值在0.998以上，RMSE值接近0，响应面模型精度很高，其中一阶模态频率响应面模型如图6所示；采用MATLAB编程对模型进行修正，修正过程支承刚度值相对改变量变化曲线如图7所示.
表3 各阶模态显著性参数筛选结果
Tab.3 Significant parameters of each order modes
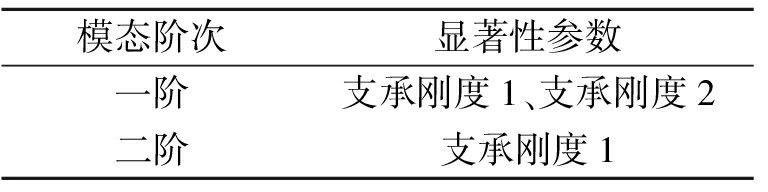
模态阶次显著性参数一阶支承刚度1、支承刚度2二阶支承刚度1
表4 响应面模型精度检验结果
Tab.4 Accuracy test results of response surface model
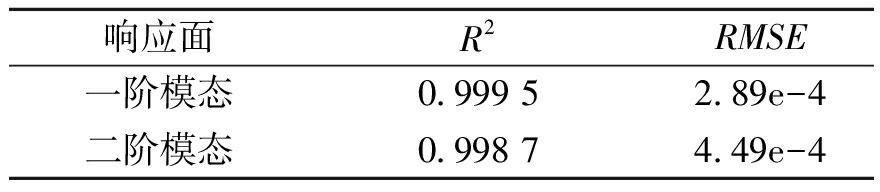
响应面R2RMSE一阶模态0.999 52.89e-4二阶模态0.998 74.49e-4
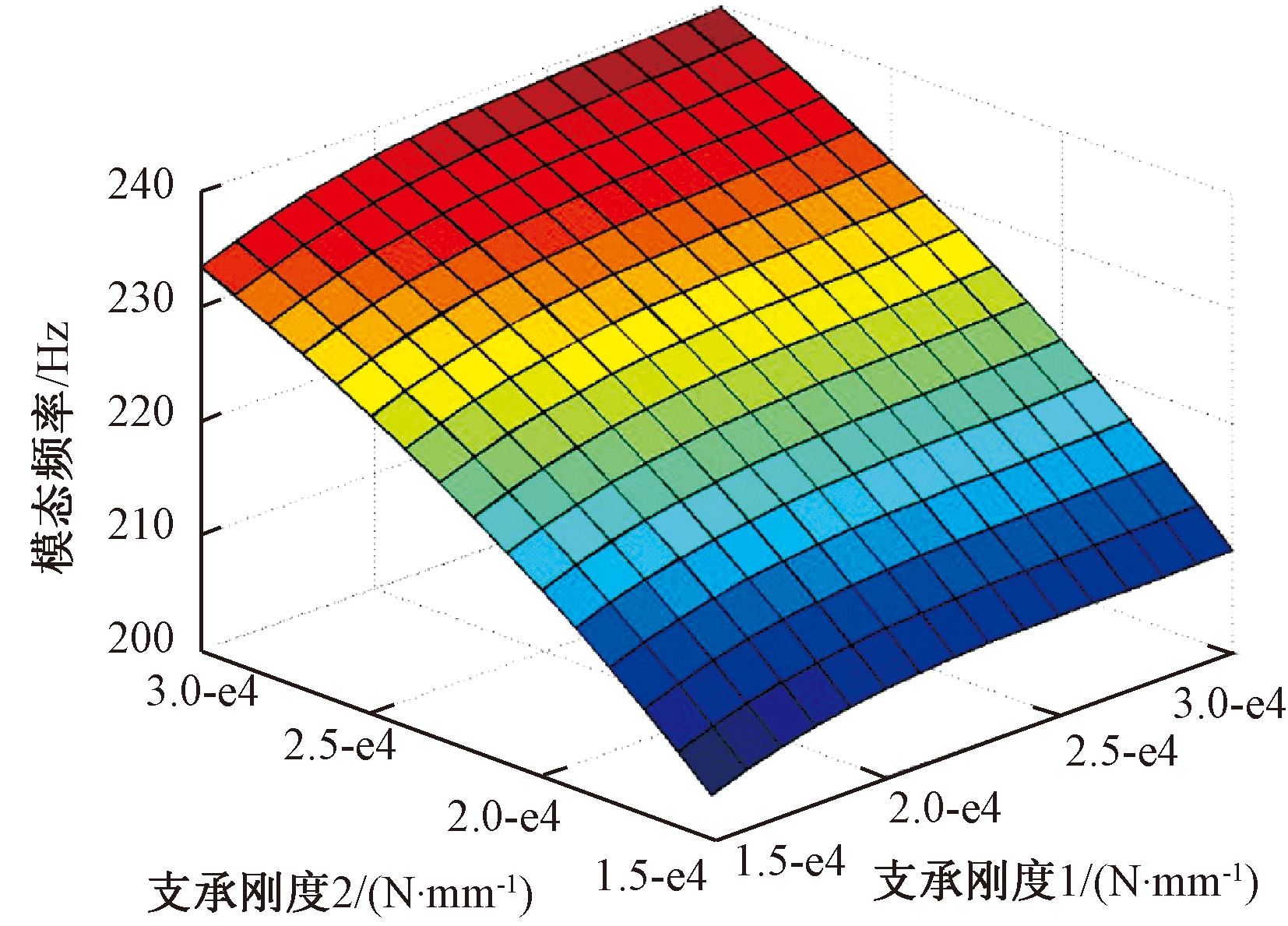
图6 一阶模态频率响应面模型
Fig.6 Response surface model of the first order modal frequency
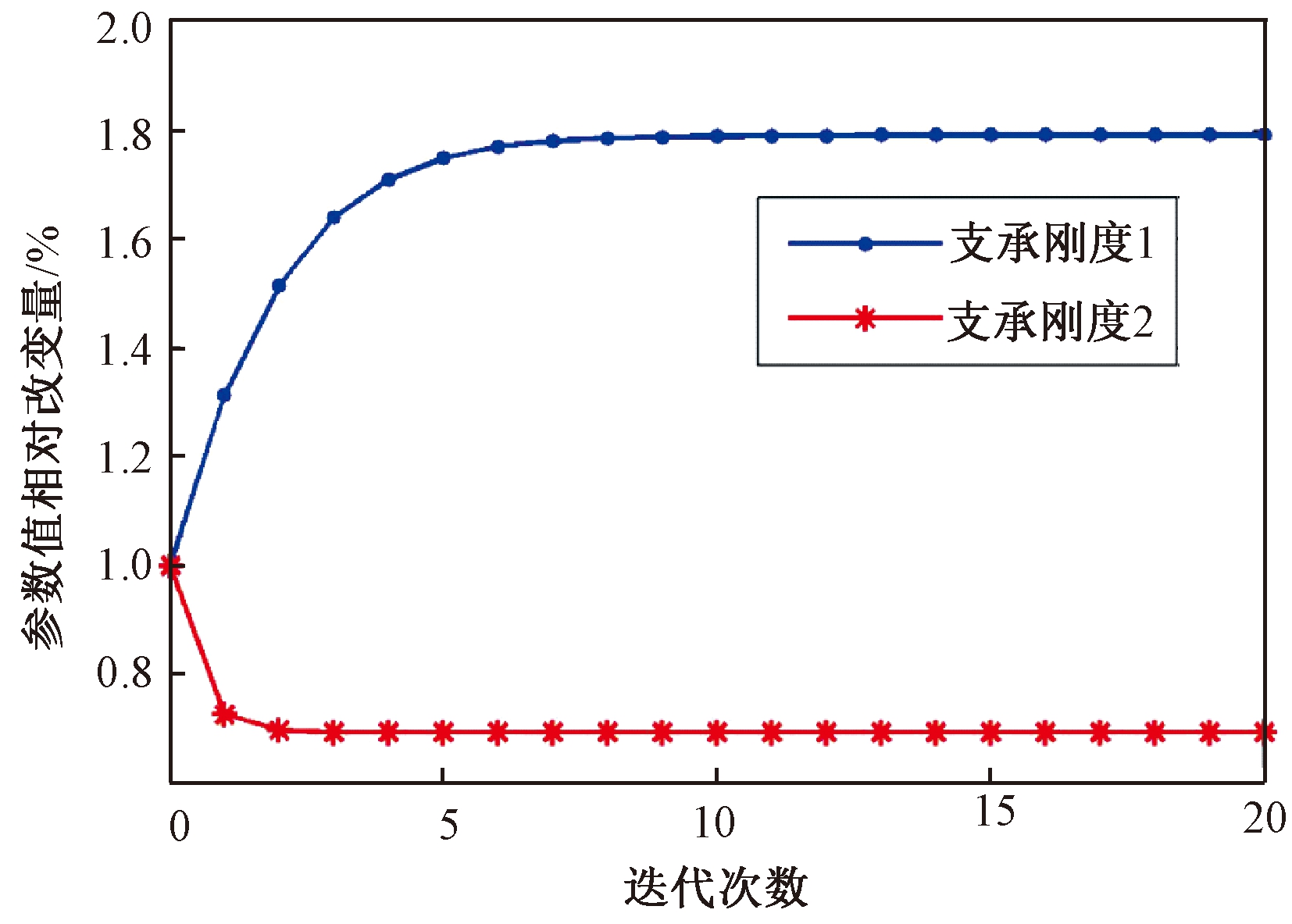
图7 支承刚度值相对改变量变化曲线
Fig.7 Relative change curve of supporting stiffness value
轴承支承刚度修正结果见表5.上述过程未对不属显著参数的支承刚度3进行识别，由于3个轴承型号尺寸相同，支承刚度值相差不大，令支承刚度3取值为支承刚度1与支承刚度2均值.对修正后的模型进行计算分析，结果如表6所示，可知修正后模态频率误差均小于0.03%，表明修正效果良好，有限元模型精度得到明显改善.
表5 子结构A轴承支承刚度值
Tab.5 Bearing stiffness values of substructure A
轴承刚度值/(N·mm-1)轴承126 883轴承220 817轴承323 850
表6 修正前后模态频率对比
Tab.6 Modal frequency comparison before and after correction
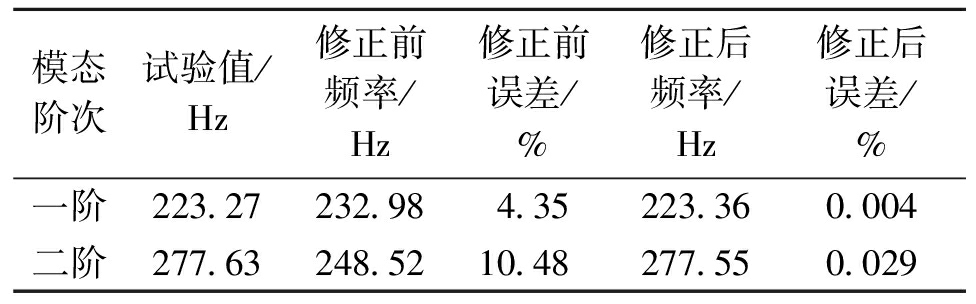
模态阶次试验值/Hz修正前频率/Hz修正前误差/%修正后频率/Hz修正后误差/%一阶223.27232.984.35223.360.004二阶277.63248.5210.48277.550.029
4.2 模态振型相关性分析
在模态试验中受到测点数量、测量频率范围、激励方式等实际测量因素的限制，可能出现测得的模态振型不完备，试验与仿真无法对应的情况.因此，为评判上述轴承支承刚度参数识别过程中仿真模型和试验模态振型的一致程度，采用了振型相关系数，即模态置信度(MAC)来计算分析[13].振型相关系数的表达式如下：
(6)
式中：
表示试验的第i阶振型向量；
表示模型的第j阶振型向量.MAC值介于0～1，越接近1说明相关性越好，工程应用中一般认为MAC值大于0.7即表示相关性良好.
计算分析子结构A模态置信度，第一阶模态MAC值为0.897 2，第二阶模态MAC值为0.913 0，表明仿真模态振型与试验振型相匹配.
4.3 频响曲线对比分析
频域分析通过不同频率谐波输入下系统的稳态响应来研究系统性能，能够深刻地反映系统参数对系统性能的影响.
对修正模型采用模态叠加法进行频率响应分析[14]，频率响应曲线如图8所示，模态试验的频响曲线如图9所示.可以看出，在修正频段(223.27～277.63 Hz)内，修正模型的仿真分析结果与试验结果接近，在修正频段外两者数据也较接近.
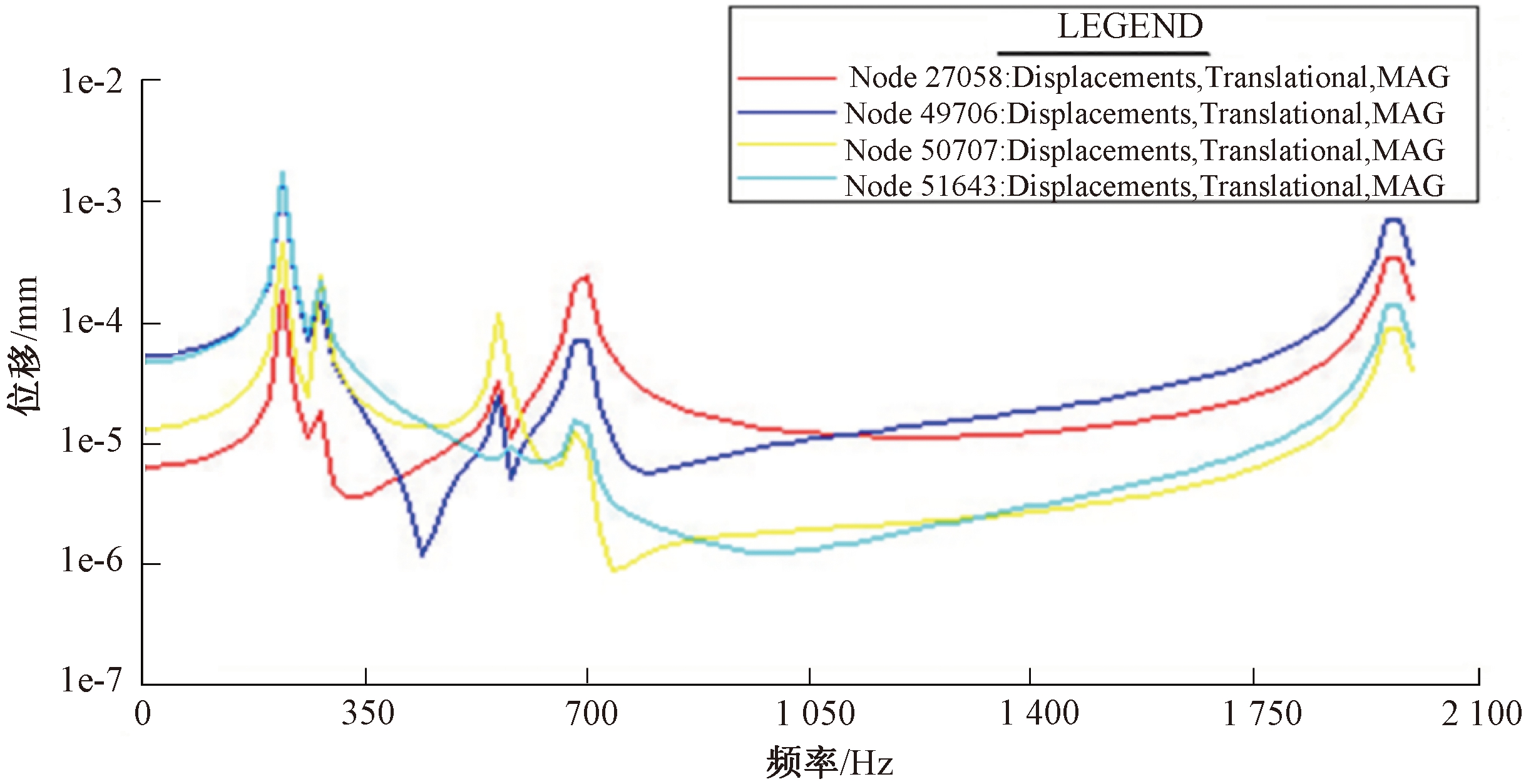
图8 子结构A有限元模型的频率响应曲线
Fig.8 Frequency response curve of substructure A finite element model
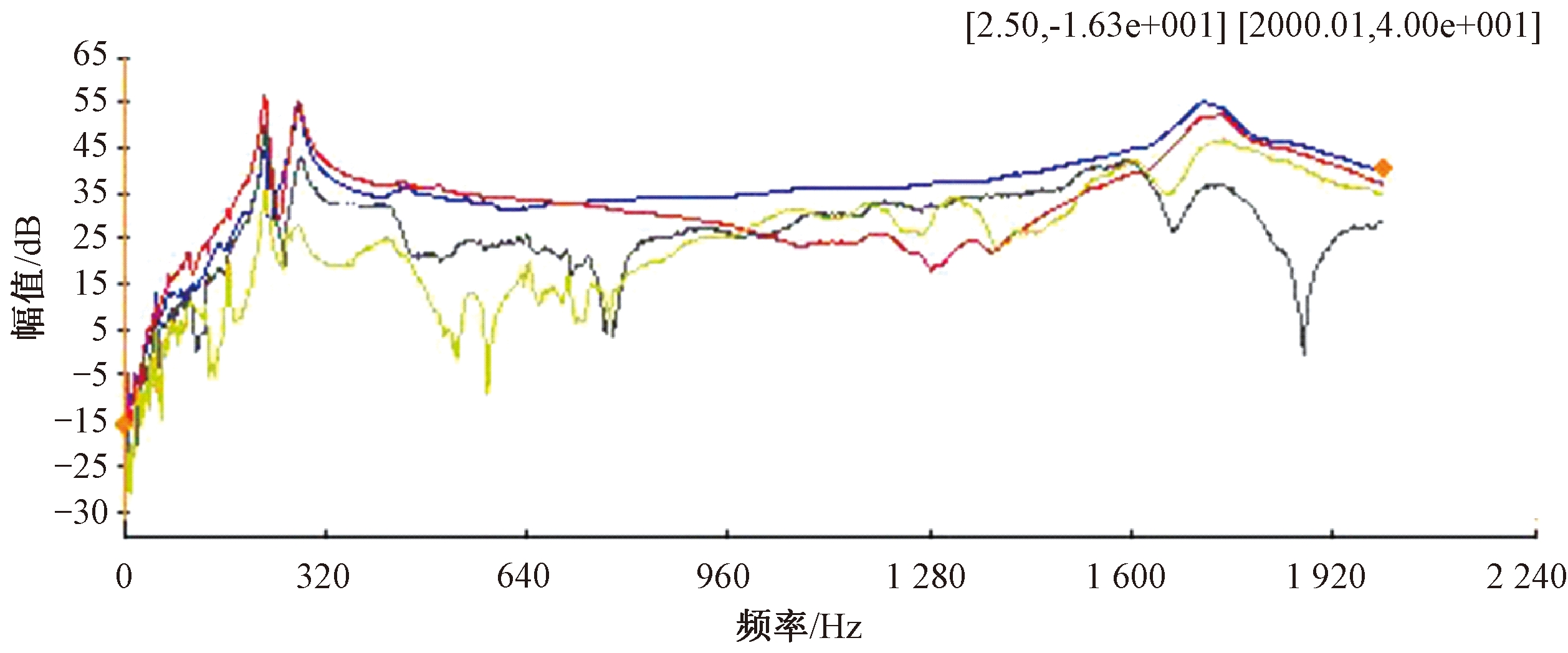
图9 子结构A模态试验的频率响应曲线
Fig.9 Frequency response curve of substructure A modal experiment
5 结论
为最终解决复杂的大型磨机传动系统有限元模型响应预测置信度的问题，笔者基于分层思想，以传动系统的子结构为研究对象，通过响应面法识别系统中的不确定性参数，对子结构模型进行修正.修正结果显示，频率误差小于0.03%，模态置信度在0.89以上，有限元模型与模态试验所得频率响应曲线接近，表明修正后的模型精度得到明显提高，能够准确反映结构的动态特性；证明了响应面法在大型磨机传动系统设计及动态特性分析中具有的良好可行性，并且为后续系统整体分析奠定了坚实的基础.
[1] 郭勤涛,张令弥,费庆国.结构动力学有限元模型修正的发展—模型确认[J].力学进展,2006,36(1):36-42.
[2] 朱跃,张令弥,郭勤涛.基于分层思想对复杂工程结构的有限元模型修正技术研究[J].振动与冲击,2011,30(12): 175-180.
[3] 秦仙蓉,潘杰,徐俭,等.塔式起重机结构有限元模型修正的响应面方法[J].振动与冲击,2018,37(06):244-250.
[4] 程军圣,余淏.基于响应面法的听小骨消声器的优化设计[J].湖南大学学报(自然科学版),2017,44(2):60-65.
[5] 陶征，刘旭，郭勤涛.响应面法用于磨机传动系统扭转振动模型修正[J].振动、测试与诊断，2016，36(6)：1222-1226.
[6] 陆森林,任栉翔.基于响应面法的车内噪声分析与优化[J].郑州大学学报(工学版),2017,38(5):65-70.
[7] 陶征,刘旭,胡斌.响应面法的杆式超声电机有限元模型修正[J].声学学报,2017,42(3):305-310.
[8] JONES D R.A taxonomy of global optimization methods based on response surfaces[J].Journal of global optimization, 2001, 21(4):345-383.
[9] 刘旭.大型机械设备齿轮传动系统的有限元模型修正研究[D].郑州：郑州大学，2016:34-36.
[10] 秦仙蓉.基于灵敏度分析的结构计算模型修正技术及相关问题的研究[D].南京:南京航空航天大学, 2001:48-51.
[11] 周美立,齐从谦,吴天星.齿轮传动系统的相似分析与设计[J].机械传动,1997(2):4-8.
[12] 胡冬奎,王平.相似理论及其在机械工程中的应用[J].现代制造工程,2009(11):9-12.
[13] ALLEMANG R J, BROWN D L.A correlation coefficient for modal vector analysis[C]//Proceedings of the 1st International Modal Analysis Conference.Orlando: USA, 1982：110-116.
[14] 龙凯,贾长治,李宝峰.Patran2010与Nastran 2010有限元分析从入门到精通[M].北京:机械工业出版社,2011：339-354.