0 引言
我国城市轨道交通的建设具有规模大、周期短、分布广、施工环境和地质条件复杂等特点.大量的市政管线将会被地铁隧道所穿越,不可避免会产生一定影响.而雨污管线的开裂或差异沉降都有可能造成周边土体性质改变,导致地面坍塌.严重的会使周围岩土稳定性发生变化,造成工程事故发生.国内外不少学者针对地铁隧道工程盾构施工对临近建(构)筑物及管道的影响进行过深入研究.理论研究方面,张治国等[1]、Vorster等[2]及Klar等[3]将弹性连续解扩展到包括沿管线的局部屈服,提出了具有节点的小直径管线连续弹性解预测公式.试验研究方面,Marshall等[4]用离心机试验验证了在隧道开挖作用下不同地层损失对相邻管线的影响.王正兴等[5]研究了在砂土条件下隧道穿越管线的相似模型试验,得出管线变形和受力与管隧间距及地层损失率有关.文献[6-11]采用有限元数值模拟方法研究了隧道施工引发地表及上覆管线的变形和应力情况.在现有成果中,隧道开挖对小直径有压管线变形和受力影响研究较多,而针对地铁隧道穿越大直径雨污管线的变形特征和应力规律则少有研究.
为弥补上述不足,笔者以北京某地铁盾构隧道穿越大直径雨污管线工程为例,采用相似模型试验和数值模拟结合的方法,对比验证雨污管线的变形特征和应力分布规律.
1 模型试验
1.1 试验原型
雨污管线材质为混凝土,采用承插式接口,管长3 m,管径2.25 m,壁厚0.175 m.研究区域内,隧道正上方为雨污管线,管线顶部距地面6.04 m.地层主要以粉质黏土为主,从地表开始向下依次为杂填土、粉质黏土、粉细砂、圆砾卵石、粉质黏土、圆砾.
隧道盾构开挖采用土压平衡式盾构机,盾构机顶部距区间地面17.45 m,隧道外径D为6 m,内径为5.4 m,衬砌为300 mm厚的C50预制混凝土管片,每环宽1.2 m,盾构机与管线间净距l为9.16 m.笔者采取管隧平行试验方案进行研究,管隧净距与隧道直径比值l/D为1.5.
1.2 相似关系的确定
文献[12] 阐述了相似正定理、相似逆定理和π定理,文献[13-14]分别从平衡方程、几何方程、物理方程(式(1)~(3))3个方面考虑建立模型试验的相似条件.
平衡方程:
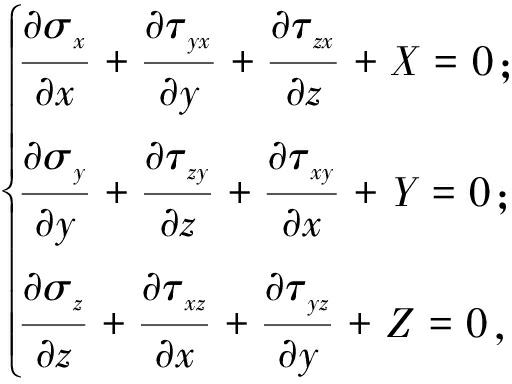
(1)
几何方程:
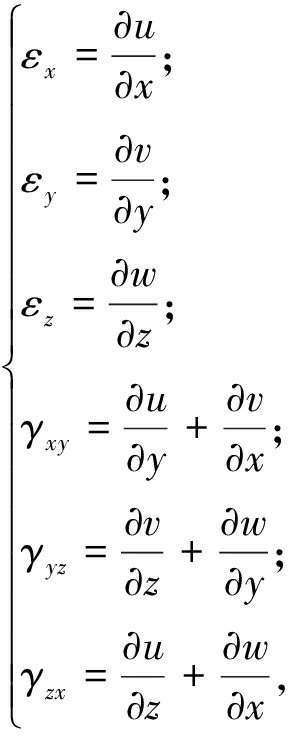
(2)
物理方程:
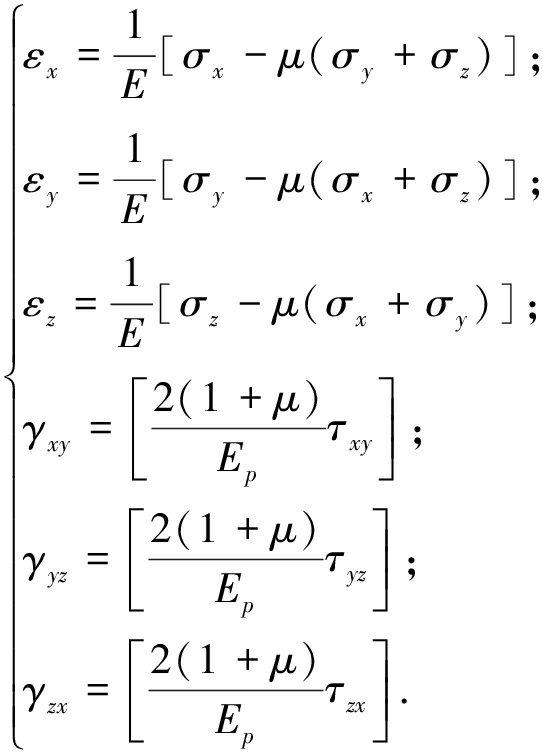
(3)
式中,X、Y、Z分别表示体积力;σ为正应力;τ为剪应力;ε为正应变;γ为剪应变.u、v、w分别是x、y、z方向的位移;E是弹性模量.σ和τ在x、y、z方向的导数分别是各方向的体力;u、v、w在x、y、z方向的导数分别是各方向的应变值.
将应力、几何及体积力的相似系数Cσ、CL、CX=CY,应变、位移、几何相似系数Cε、Cδ、CL和应变、应力、弹性模量、泊松比的相似系数分别代入式(1)~(3),可得到CY CL/Cσ=1,CεCL/Cδ=1,Cσ/CεCE=1.因此,重力与泊松比的相似系数可确定为1∶1,模型试验的几何相似、应力、位移、弹性模量以及黏聚力的相似系数可确定为15∶1.
1.3 模型箱及盾构隧道开挖方案
试验装置为地下工程试验模型箱,模型箱尺寸为3 m×1 m×2 m(长×宽×高).模型箱由钢化玻璃、有机玻璃、基准梁和角钢组成,同时采用螺栓连接,如图1所示.

图1 试验模型箱及盾构装置
Fig.1 Model test box and shielding apparatus
模型试验中,管线的布设和盾构隧道开挖与工程原型相同,见图2所示.盾构隧道模拟采用预制不锈钢圆形掘进装置来实现,如图1(b)所示.其中,不锈钢弹性模量为14 GPa.盾构隧道模型壁厚20 mm,外径400 mm,内径360 mm,长度1 000 mm;选取加筋石膏作为管节,管节直径150 mm,管壁厚10 mm,每根管节长200 mm,管线总长为1 000 mm,管顶埋深0.4 m.模型箱的四周和底板均采用角钢和螺栓固定,并在钢化玻璃拼接处用加劲肋进行加固,限制模型箱四周的侧向移动变形,从而达到消除边界效应影响的目的.
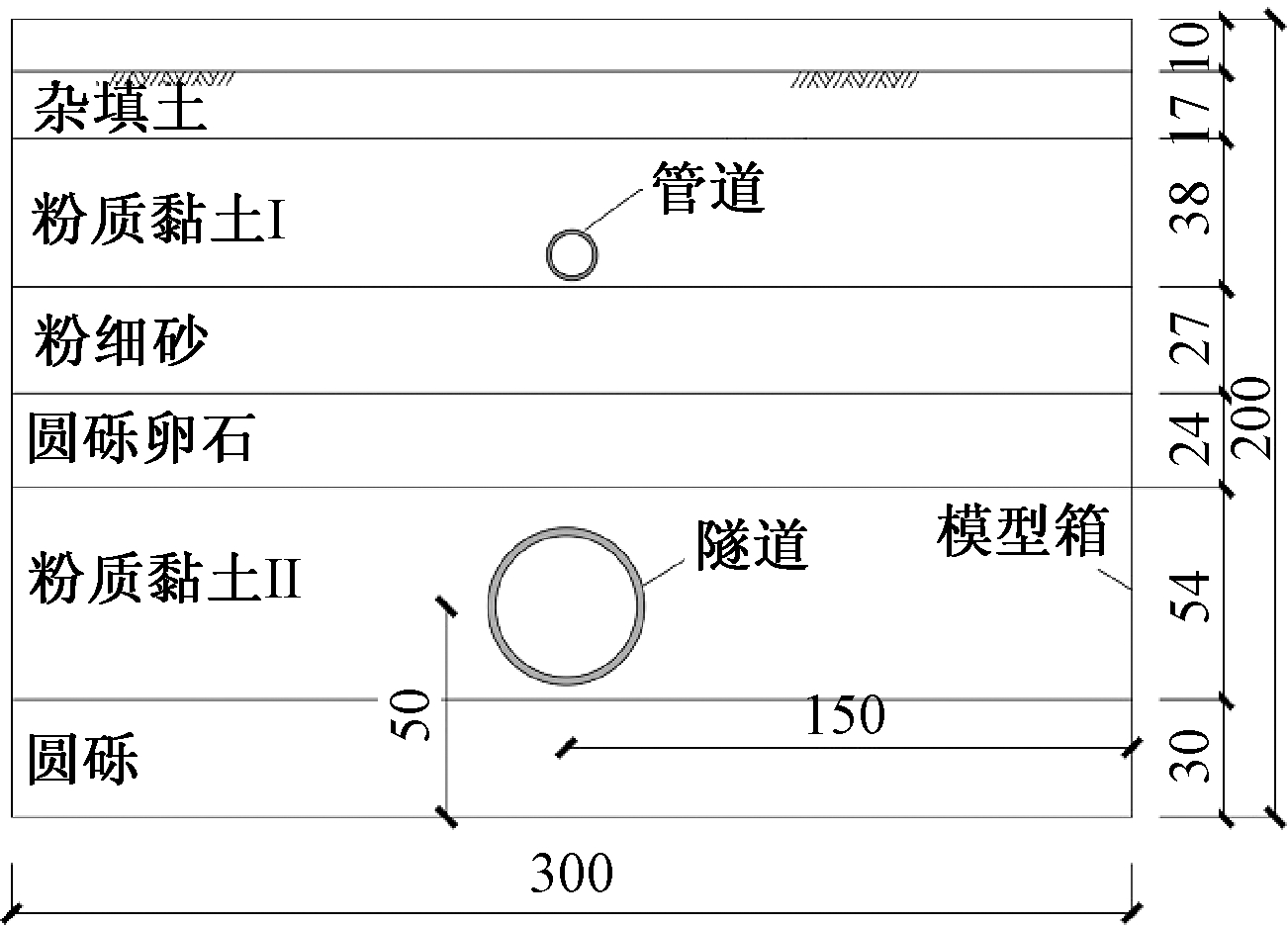
图2 管线与盾构隧道平行方案(单位:cm)
Fig.2 Relative position of pipeline and shield tunnel (unit: cm)
1.4 相似材料与试验量测方案
模型试验地层采用河砂、铁粉、石灰与石膏4种材料制作.其中骨料为河砂与铁粉,胶黏剂为石膏与石灰.黏聚力可通过直剪试验测定,具体参数见表1.相似材料组成配比如表2所示.
选用加筋配置的石膏模拟模型试验的管线,将石膏的抗压强度控制为2 MPa,弹性模量控制为2 000 MPa.
表1 模型材料物理力学参数
Tab.1 Physical and mechanical parameters of model materials
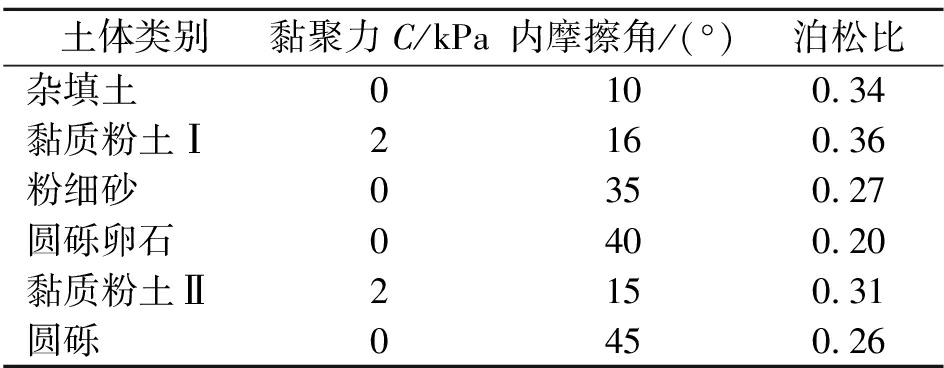
土体类别黏聚力C/kPa内摩擦角/(°)泊松比杂填土0100.34黏质粉土Ⅰ2160.36粉细砂0350.27圆砾卵石0400.20黏质粉土Ⅱ2150.31圆砾0450.26
表2 相似材料组成及配比
Tab.2 Composition and ratio of similar materials
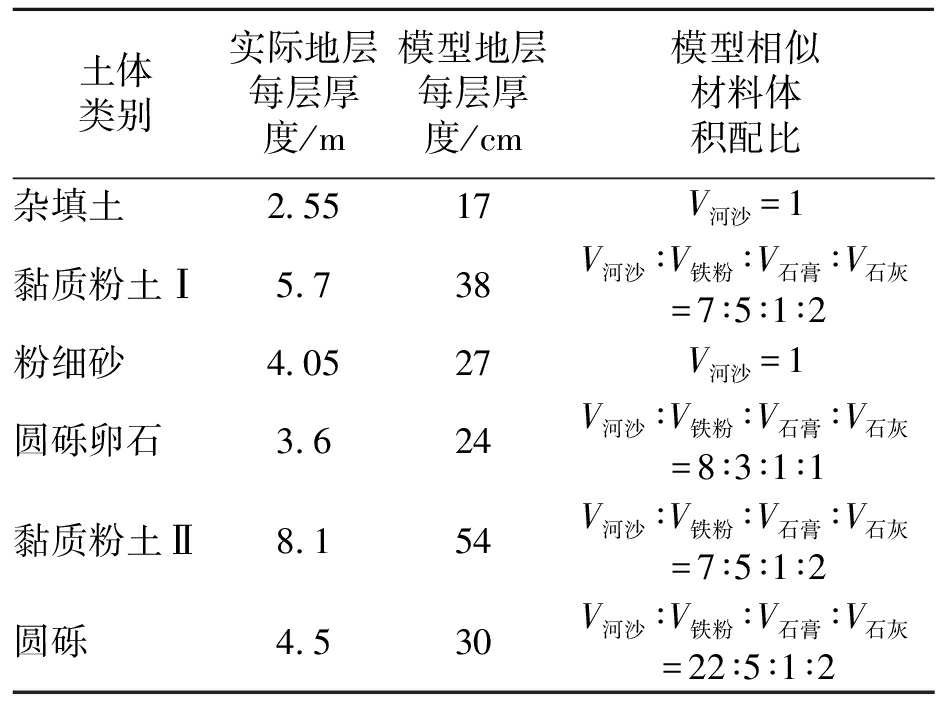
土体类别实际地层每层厚度/m模型地层每层厚度/cm模型相似材料体积配比杂填土2.5517V河沙=1黏质粉土Ⅰ5.738V河沙∶V铁粉∶V石膏∶V石灰=7∶5∶1∶2粉细砂4.0527V河沙=1圆砾卵石3.624V河沙∶V铁粉∶V石膏∶V石灰=8∶3∶1∶1黏质粉土Ⅱ8.154V河沙∶V铁粉∶V石膏∶V石灰=7∶5∶1∶2圆砾4.530V河沙∶V铁粉∶V石膏∶V石灰=22∶5∶1∶2
模型试验需要量测内容有:管线的沉降和应力.管线沉降采用拉线位移传感器,其量测范围为0~500 mm,精度为0.01 mm.管线应力采用电阻应变片及DH3816N静态应变测试系统.量测设备布设如图3.图4为承插口管节接口设计及应变片布设.拉线位移传感器固定在基准梁上,分别标记标号;在每根管节前后分别钻有小孔,将拉线穿过小孔并固定于管节内部,分别标记为A、B;在每根管节的顶部和底部分别粘贴两个应变片,记号为D-1/2和D-3/4,如图3所示.
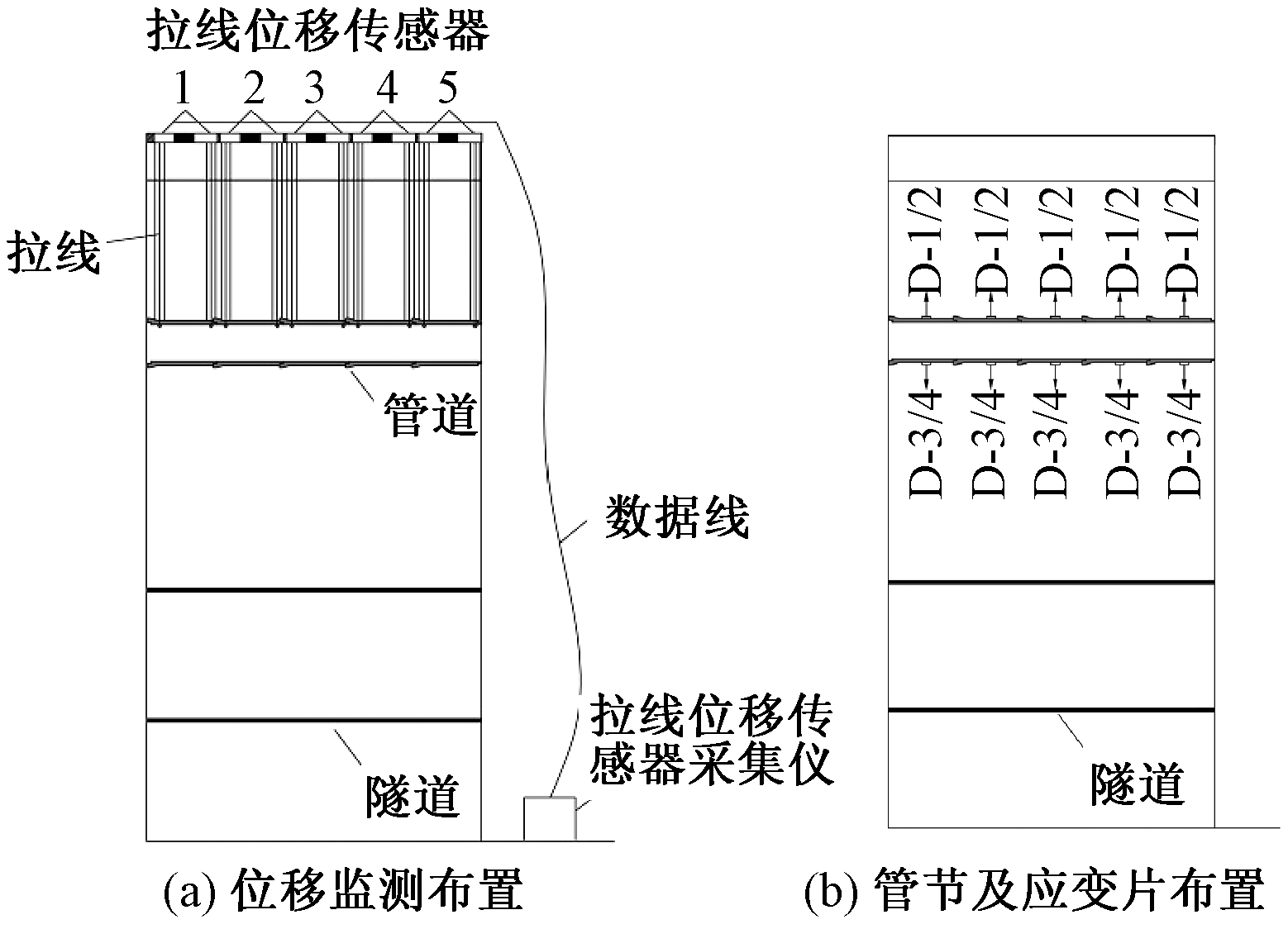
图3 量测设备布设
Fig.3 Measurements layout of pipe
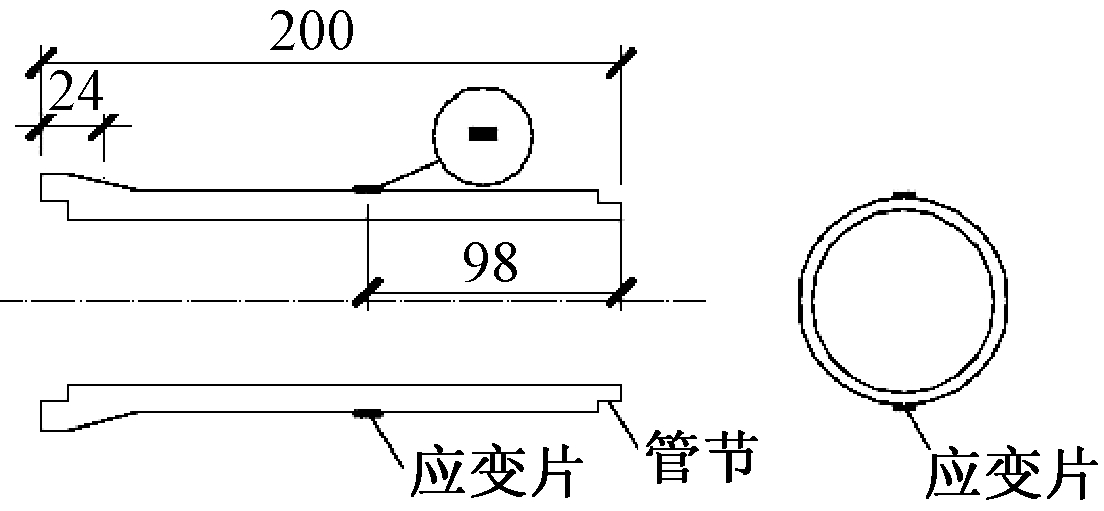
图4 管节接口及应变片布设(单位:mm)
Fig.4 Joint of pipe and layout of strain gauge(unit:mm)
1.5 模型试验过程
①首先埋设管线,将模拟地层填埋至设计高度,静止放置24 h充分固结达到稳定.②分20步工序模拟盾构施工过程,每步工序掘进5 cm,总计掘进深度100 cm.掘进间隙预留10 min,同时采集应变片及拉线位移传感器的数值.③盾构隧道开挖结束,在自重作用下模拟地层及管线分别固结4、12、24、48 h并记录下各时刻的管线位移值和管节应变.
1.6 试验结果分析
1.6.1 管线位移分析
根据相似比将试验结果恢复至工程原型.记录管线监测点的位移值及稳定后的管线整体位移分布,具体见图5、图6.由图5看出,随着盾构隧道开挖距离的增加,管线沉降不断增大,最终达到10 mm;隧道开挖结束并进入稳定静置状态后,受掌子面开挖造成的地层损失影响,隧道周围土体应力向隧道所在位置集中,土颗粒间隙被进一步挤密从而带动管节产生较大沉降,待模型静置 48 h达到稳定状态后沉降值最大接近20 mm.从图6可看出,管线沉降近似为一平缓曲线,沉降值为18 mm.
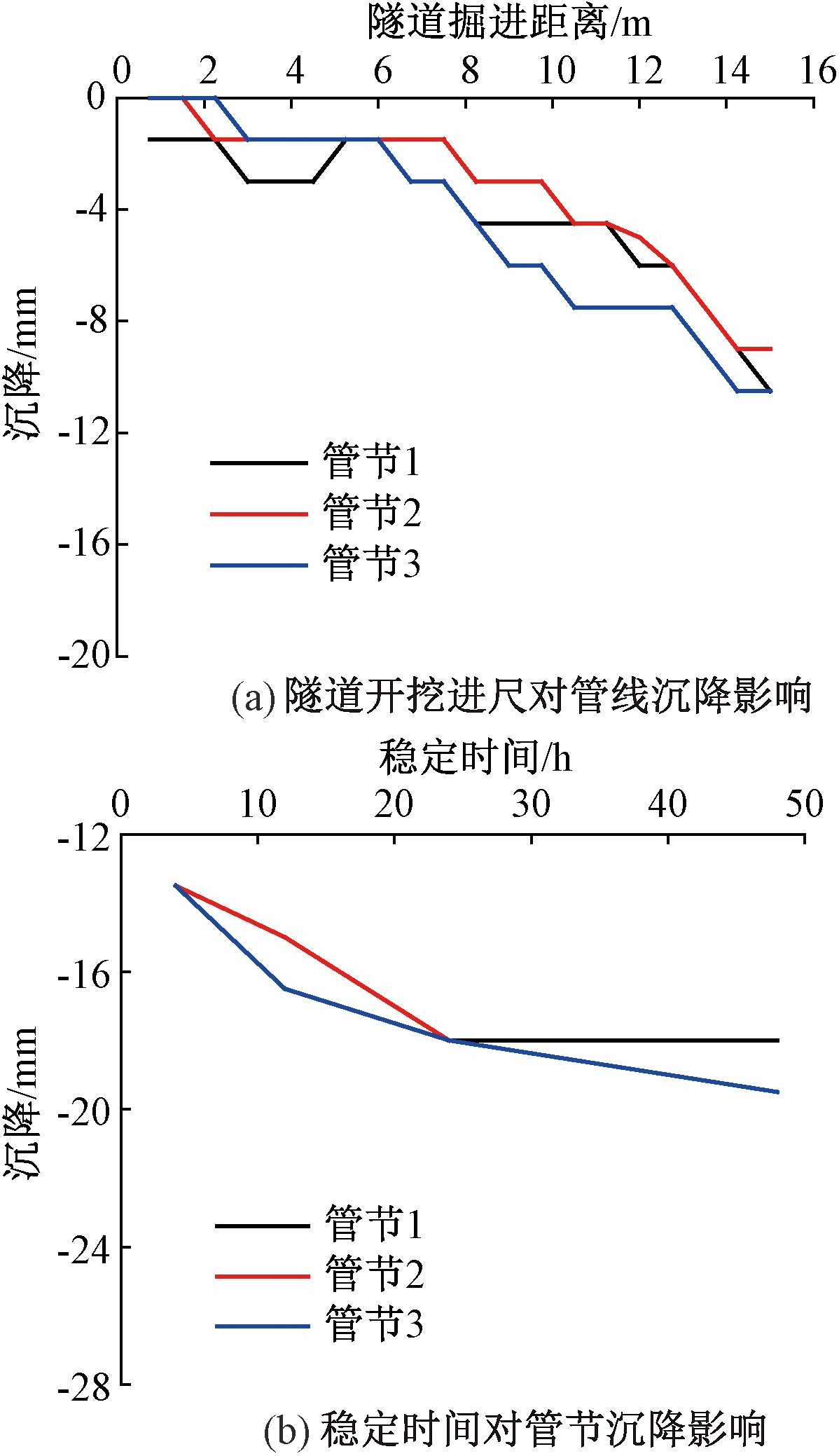
图5 开挖进尺对管线沉降影响
Fig.5 Influence curve of excavation on pipeline settlement
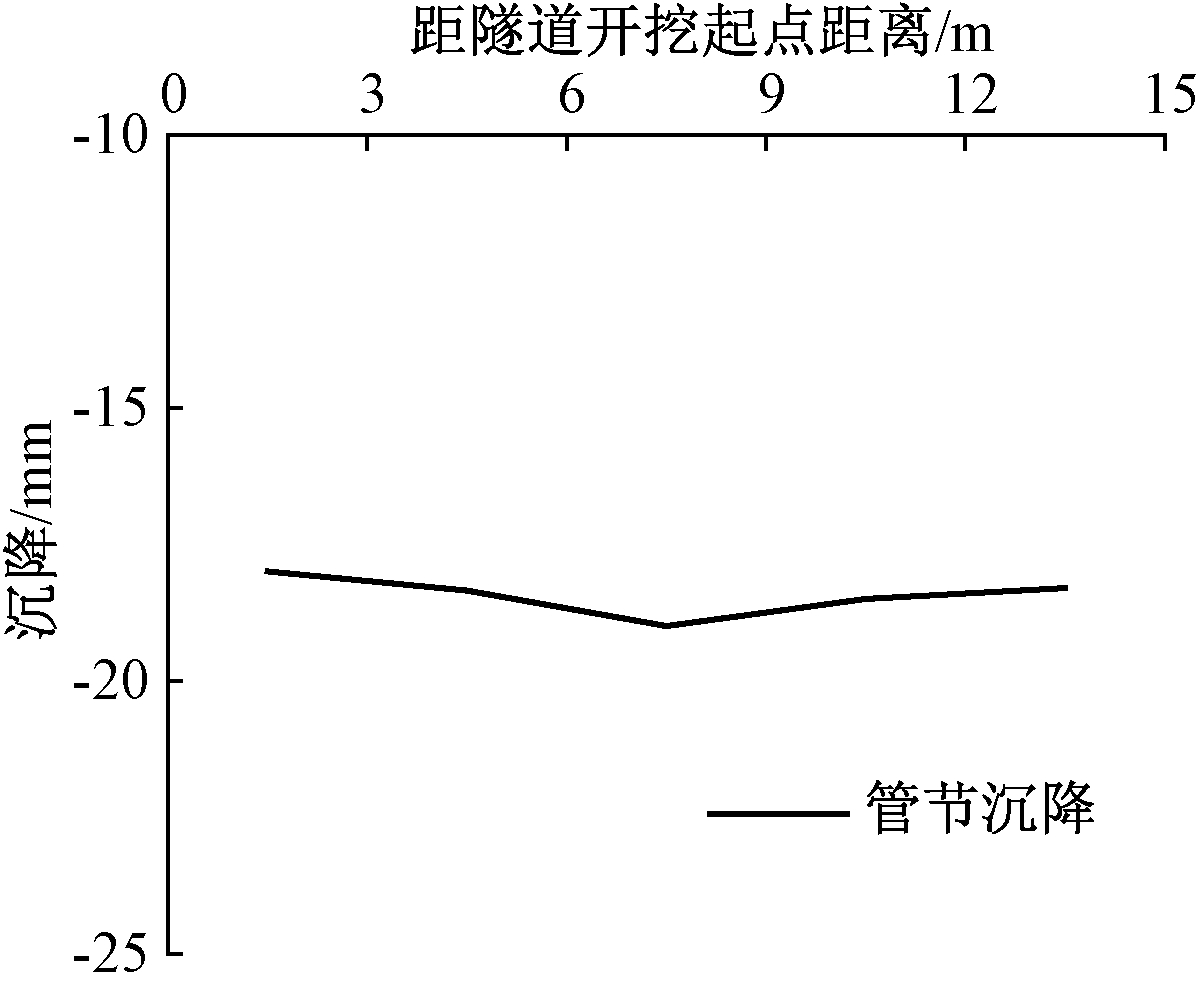
图6 管线沉降曲线
Fig.6 Settlement curve of pipe
1.6.2 管线顶部与底部应力分析
研究管隧交点正上方处管节顶部与底部应变平均值.开挖进尺对管节应力影响如图7所示,管线应力曲线如图8所示.分析图7可得,随着盾构隧道开挖的进行,管节的顶部和底部基本处于受拉状态,当开挖进展达到15 m时,顶部受拉应力达到135 kPa,大于底部应力;当隧道盾构开挖结束并静置一段时间后,顶部应力持续增大,而底部应力略有减小.管节顶部和底部应力在静置48 h后趋于稳定值,顶部应力接近240 kPa,底部应力接近70 kPa.分析图8可得,管节顶部和底部应力均为正值,表明隧道开挖后引起地层损失造成土体向隧道方向移动,管线底部受拉,而顶部土体在向下挤密过程中对管线顶部也造成受拉状态.因此在实际工程中,需做好对管线的抗拉防护措施.
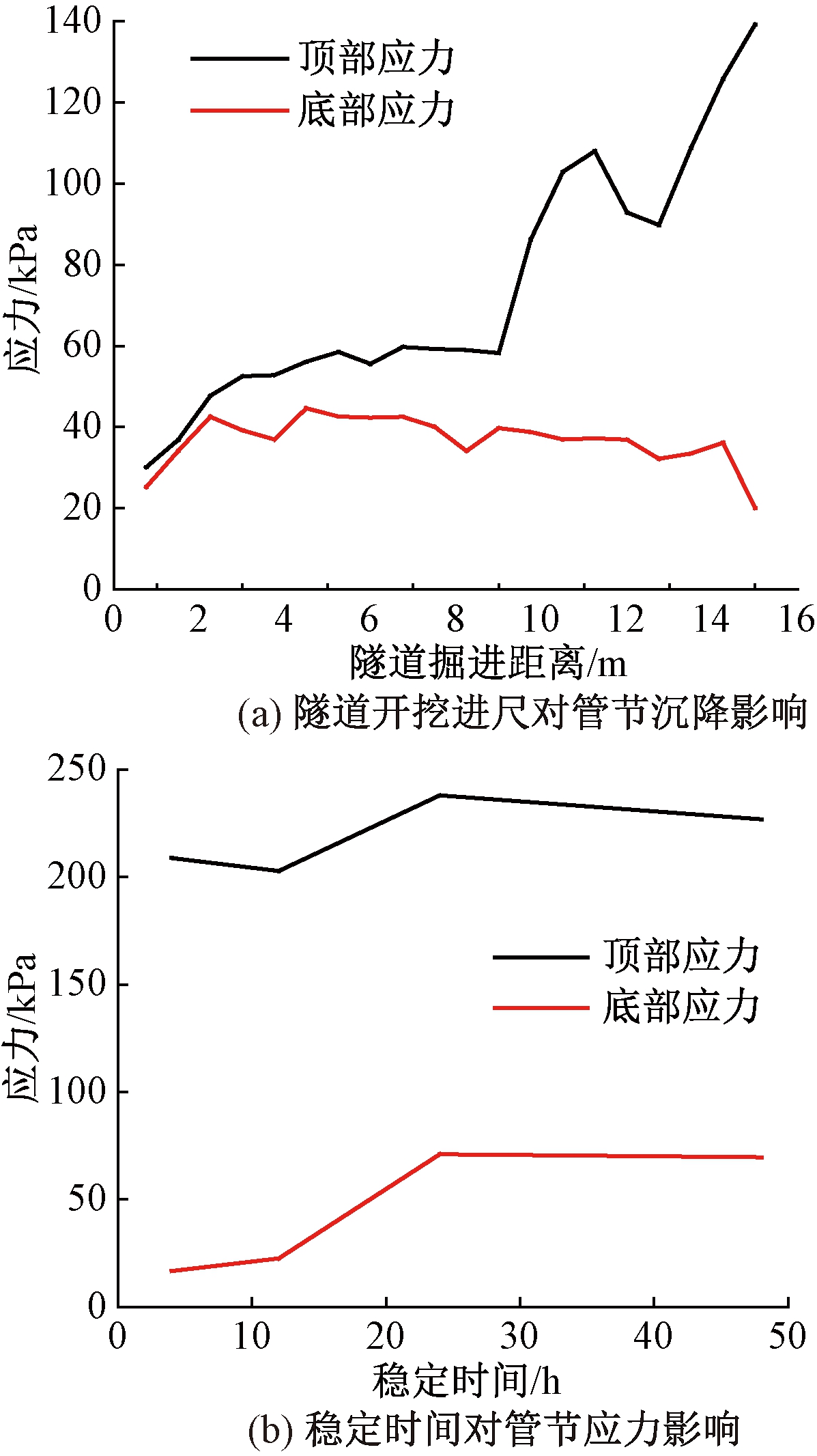
图7 开挖进尺对管节应力影响
Fig.7 Influence curve of excavation pipeline stress
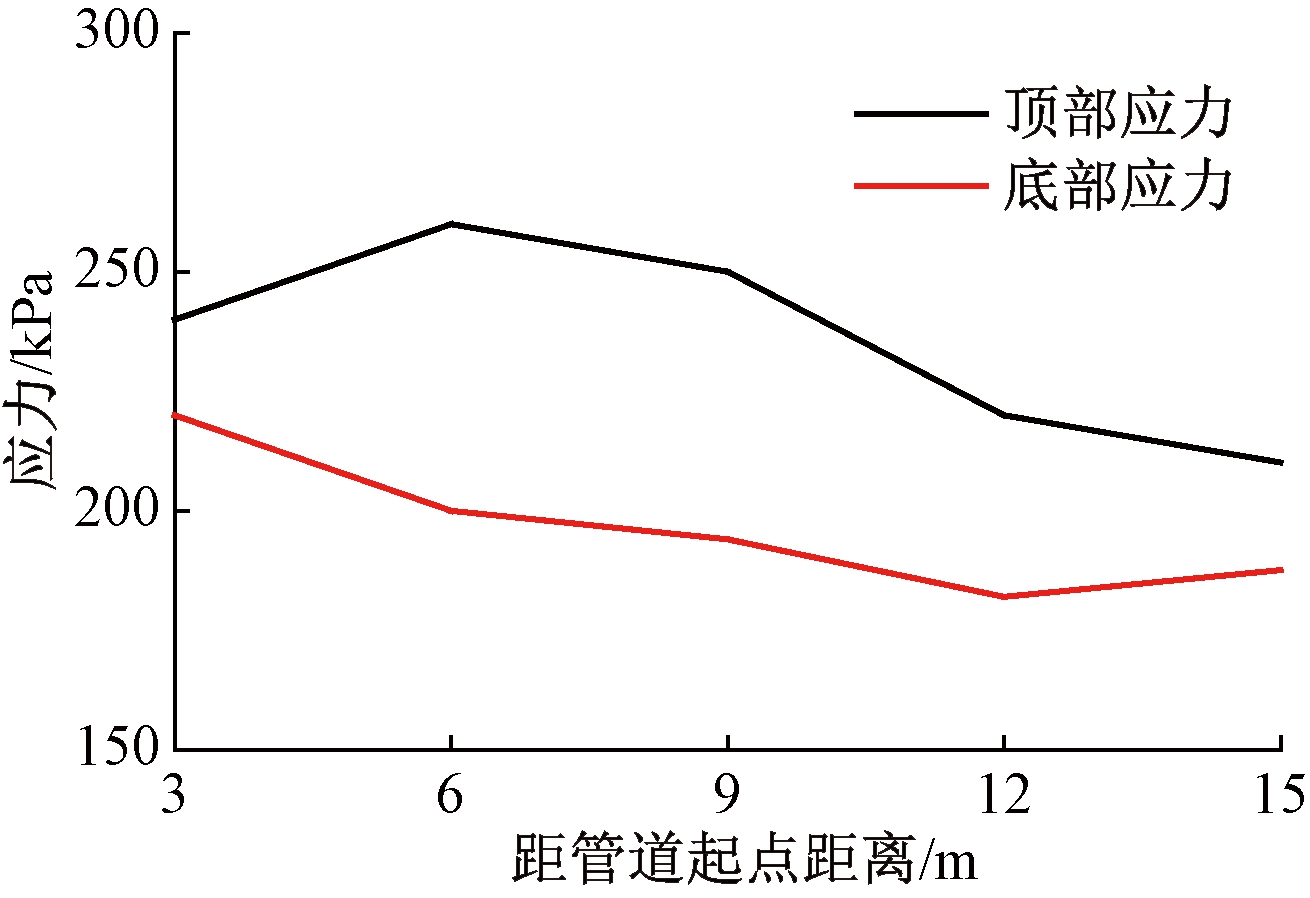
图8 管线应力曲线
Fig.8 Stress curve of pipe
2 数值模拟试验
2.1 模型范围及网格划分
采用Midas GTS NX软件对盾构隧道施工过程中的管线变形和应力变化进行数值模拟,主要针对管线沉降、应力特征进行研究.为满足边界效应要求,隧道外围土体范围需取3倍以上隧道直径长度,因此模型长、宽、高分别为60 m×45 m×30 m.采用定义线性梯度的方法划分网格,可使管线附近网格相对密集而边界处网格相对稀疏.分别在管节承插口部位设置接触面,模拟盾构隧道施工期间管节的相互错动.模型网格划分如图9(a)所示,管线和隧道网格划分如图9(b)、(c)所示.设置承插口长0.12 m,管壁长2.88 m.
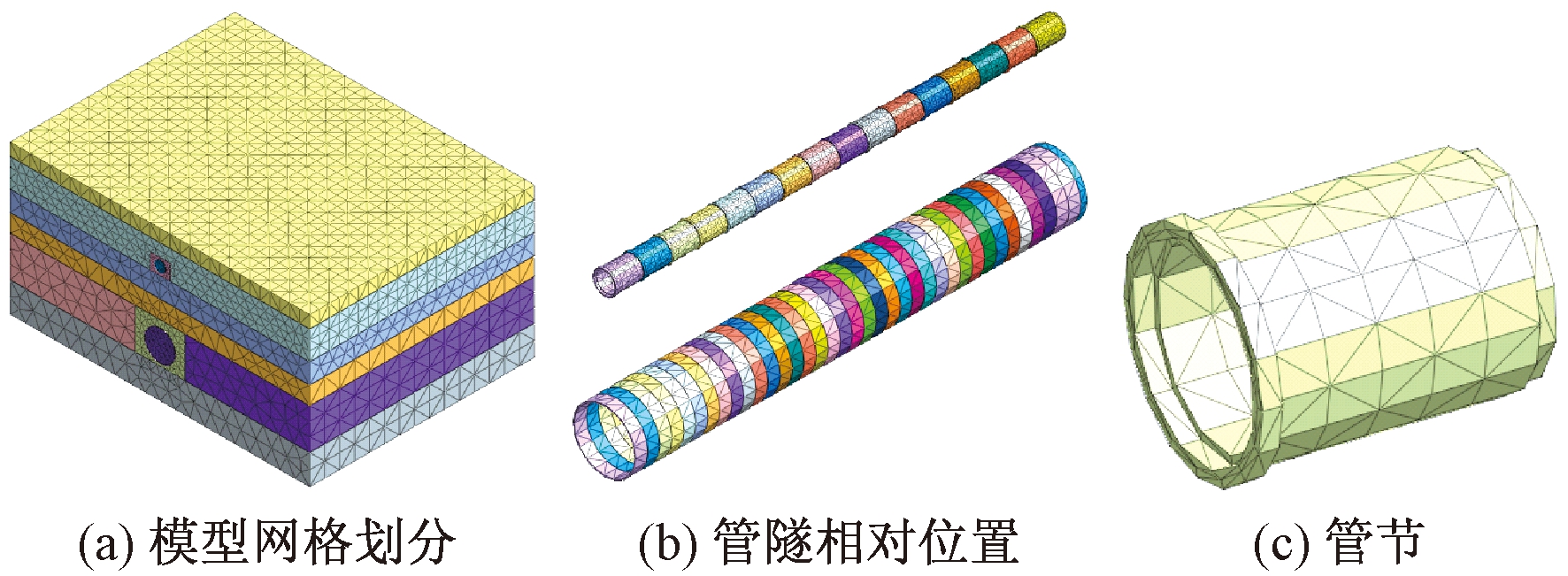
图9 数值模型网格划分
Fig.9 Mesh of calculated numerical model
2.2 模型计算参数选取
管线、盾构管片及注浆层均采用弹性本构模型,土层选用摩尔-库仑本构模型.构件均采用实体单元,盾壳采用板单元.依据岩土勘察报告,将土层力学参数相近的土层合并为5层.
接触面的切向刚度取900 MPa,法向刚度取1 260 MPa.盾构管片选用C50混凝土,壁厚为300 mm,隧道掌子面上施加300 kPa的应力模拟施工压力.考虑到隧道上方土压力的影响,采用水泥砂浆作为注浆层,注浆等代层的厚度取150 mm,可防止隧道上方地表出现过大沉降.并在掌子面径向施加150 kPa均布力模拟注浆压力.具体参数详见表3.
表3 计算模型物理力学参数
Tab.3 parameters of soil layers
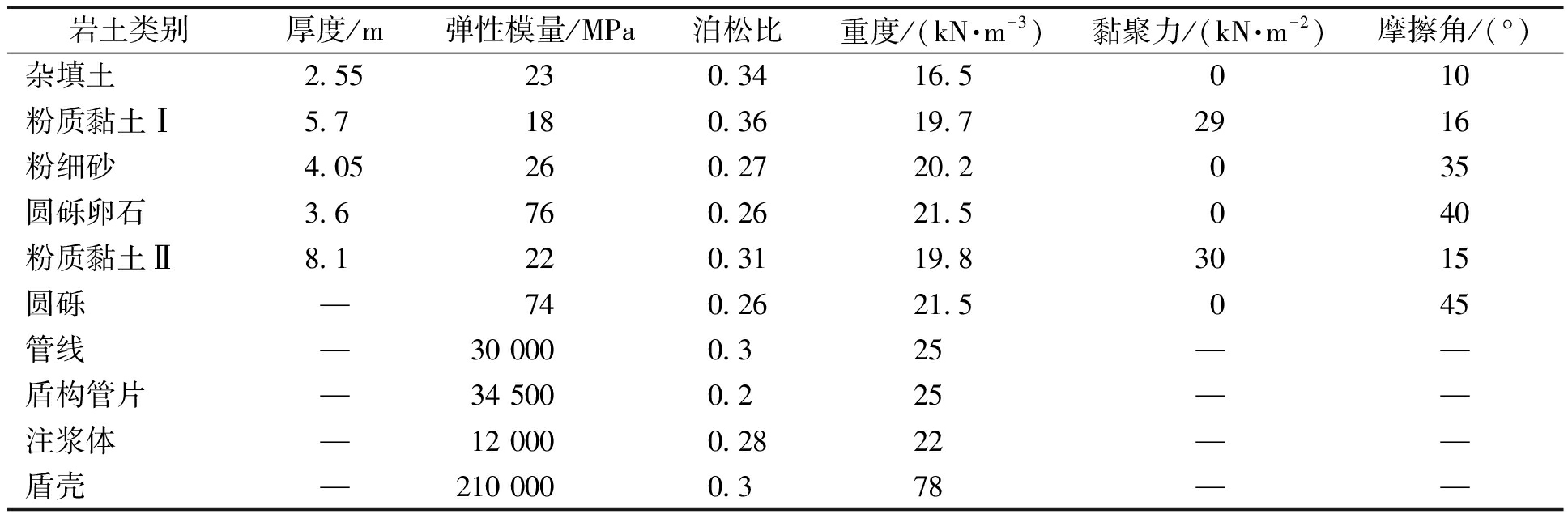
岩土类别厚度/m弹性模量/MPa泊松比重度/(kN·m-3)黏聚力/(kN·m-2)摩擦角/(°)杂填土2.55230.3416.5010粉质黏土Ⅰ5.7180.3619.72916粉细砂4.05260.2720.2035圆砾卵石3.6760.2621.5040粉质黏土Ⅱ8.1220.3119.83015圆砾—740.2621.5045管线—30 0000.325——盾构管片—34 5000.225——注浆体—12 0000.2822——盾壳—210 0000.378——
2.3 边界条件确定
模型四周设置位移边界条件约束水平运动,底部设置位移边界条件约束竖向运动,模型上表面为不设置边界条件即自由边界.
2.4 监测点的布设
为研究管节前后位移,需在管节前后设置沉降监测点.为研究管节中部和接口轴向应力,需在每个管节设置4个应力监测点.沉降监测点和应力监测点设置如图10、图11所示.
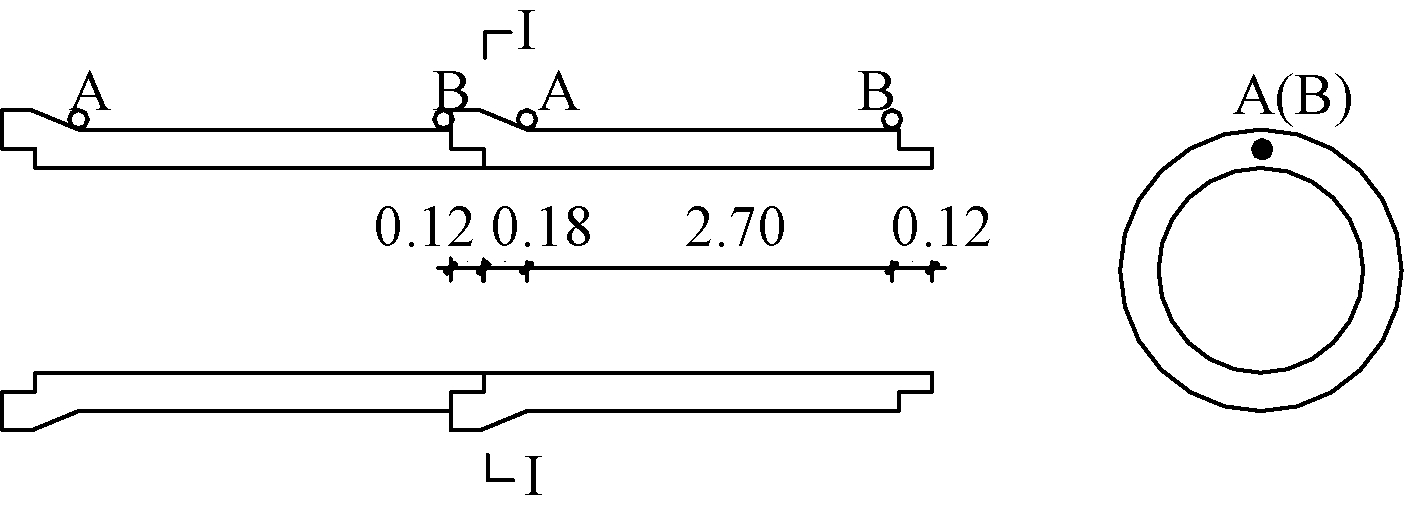
图10 管节沉降监测点布置(单位:m)
Fig.10 Layout of settlement observation points on the pipe section(unit: m)
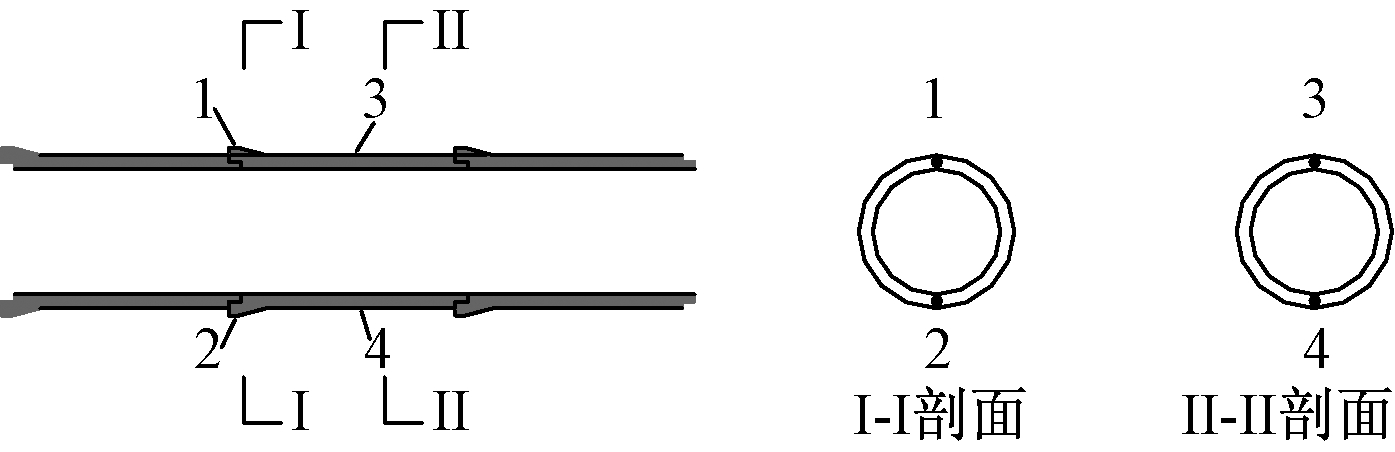
图11 管节应力监测点布置
Fig.11 Layout of stress observation points on the pipe section
2.5 数值计算工序
数值模拟计算的工序与模型试验基本相同,隧道盾构施工过程采用网格激活-钝化的方式来实现.隧道盾构开挖采用“钝化”命令,管线和隧道管片及注浆的属性采用“激活”命令.模拟工序如下:1)计算土体在自重下的初始应力场,提高收敛判别条件,土体固结稳定后,清零位移;2)“激活”管线模型,提高收敛判别条件,模拟管线施工完成后的应力场分布,清零位移;3)定义盾构隧道施工工况,按照如下施工阶段进行:土体开挖、盾壳安装、管片安装、盾尾注浆;4)依次循环第3 步至开挖完成.从隧道开挖至结束、土体达到稳定状态共计38 步;5)计算结果及后处理分析.
2.6 数值计算结果分析
2.6.1 管线位移分析
图12为管线竖向位移在模型试验与数值模拟计算中的对比曲线.由图12(a)、(b)可知,数值计算与试验测得的管线沉降影响曲线均呈折线变化,表明管线变形随施工步序的增加经历了线弹性和非线性变化两个阶段.在施工初期,由于隧道掌子面开挖导致的地层损失,数值计算曲线和模型试验曲线都出现减小趋势.模型地层在配制时可能出现搅拌不均,而数值计算选用的参数偏于理想化,因此数值计算曲线呈现出凹型变化而模型试验曲线为凸型变化;施工后期,两组曲线均呈现出非线性减小,后开挖土体产生的地层损失对该管节的影响逐渐减弱.进入稳定状态后,数值计算和模型试验结果相差不大.由图12(c)可知,数值模型中材料参数的理想化导致非线性减小过程中有限元得出管线沉降值与试验值之间的误差均在10%以内.进入稳定状态后,管线沉降分布曲线与试验值能较好的吻合,表明在隧道施工过程中管线沉降变化规律相同,说明了建模方法的合理性.
2.6.2 管线应力分析
管线中部监测点1、2的应力时程和应力分布如图13所示.由图13看出,管节顶部和底部均为受拉状态,在隧道盾构开挖结束前,管线应力缓慢增长.在静置稳定过程中,管线顶部和底部应力增长较快,且顶部拉应力大于底部.
图14(a)、(b)为隧道开挖进尺对管节应力影响,图14(c)为管线顶部所受应力对比.由图14(a)、(b)可知,随着隧道的开挖,管线顶部应力为受拉状态,在隧道开挖结束前,由于模型地层配制和有限元参数选取的理想化,数值计算结果略小于模型试验;当隧道开挖结束静置稳定48 h后,数值结果与模型试验结果基本吻合.分析图14(c)可知,管节顶部与底部均为受拉区,数值计算结果和模型试验基本吻合.
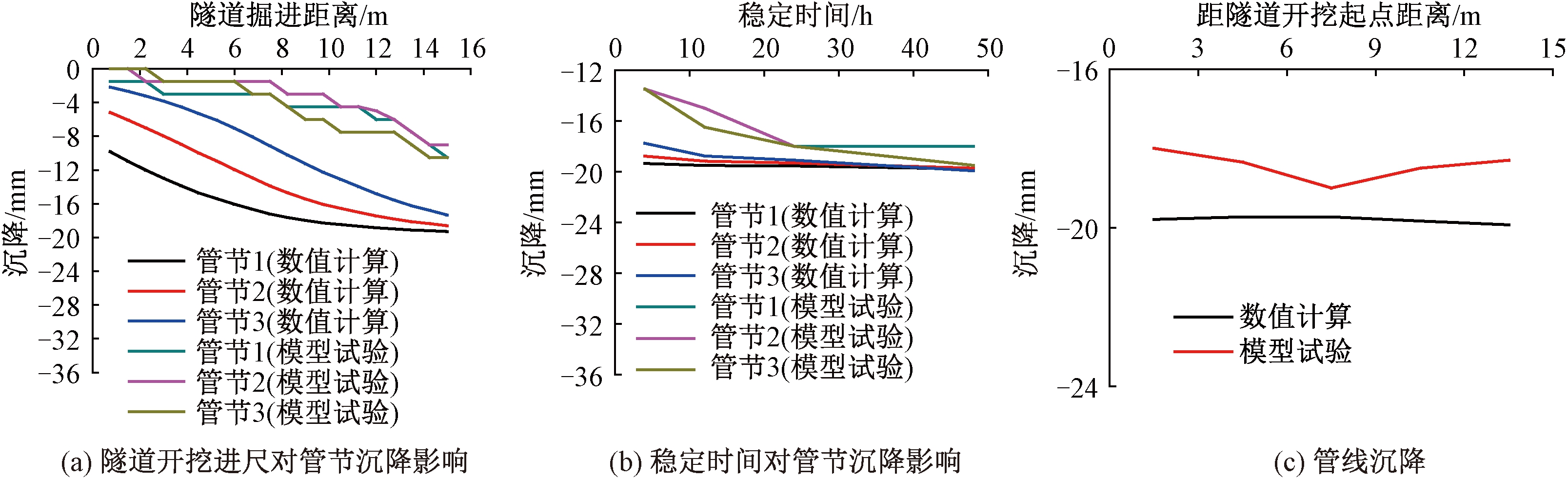
图12 模型试验与数值计算中管线位移结果对比
Fig.12 Comparison between model test and numerical calculation of pipe displacement
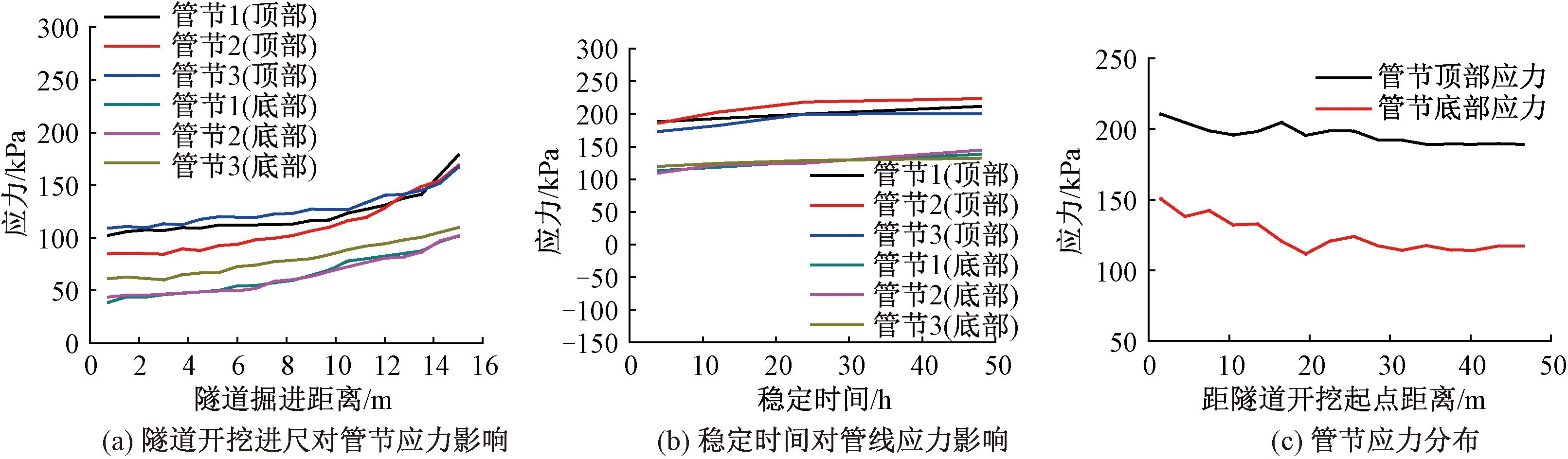
图13 管节应力曲线
Fig.13 Stress curve of pipe
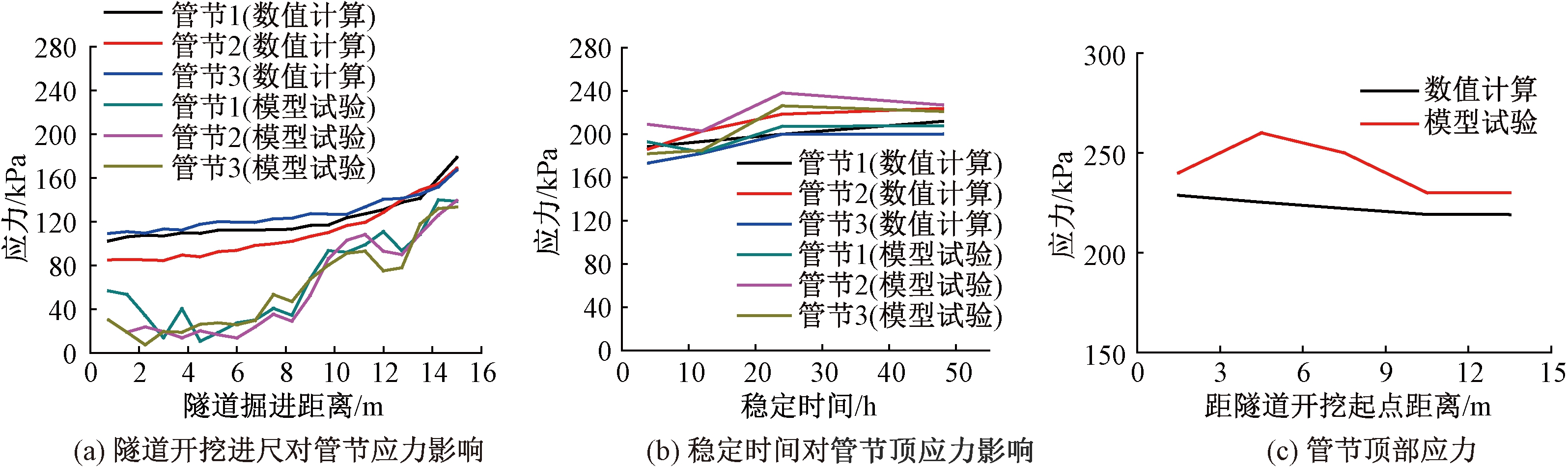
图14 模型试验与数值计算中管节应力对比
Fig.14 Comparison between model test and numerical calculation of pipe stress
有限元与试验测得管线应力分布曲线基本呈现平缓分布,两种曲线均反映出相同的应力分布规律.管节顶部与底部均为受拉区,表明随着盾构隧道开挖的进行,管线底部由于土体应力向隧道方向集中而导致管线周围土体颗粒被挤密,向管线下方移动,从而带动管线底部和顶部均产生拉应力.数值试验结果略小于模型试验,两者之间误差均在10%以内.
3 结论
通过对管隧平行条件下模型试验与数值模拟结果进行对比,针对盾构隧道开挖引发上覆雨污管线的影响进行研究,得出如下主要结论:
(1)模型试验与数值模拟结果基本吻合,验证了数值模拟的有效性.
(2)地铁盾构隧道施工时,管线沉降呈现平缓分布,最大值出现在盾构隧道尾部上方管节处.研究发现,当管隧净距l与盾构隧道直径D比值l/D为1.5时,需在掌子面距盾构隧道尾部1.5D范围内(隧道开挖进尺方向)加密监测点布设,提高监测频率.
(3)随着隧道开挖与土层沉降累积,管线上覆荷载逐渐增大;在隧道开挖过程中,盾构隧道上方管节应力分布小幅波动,总体呈现平行分布趋势.当l/D为1.5时,管线顶部与底部均为受拉状态,说明隧道开挖对管节影响主要为受拉.因此沿管线分布范围内需对管节进行防护措施,避免出现受拉破坏.
由于笔者采用的模型试验及数值模拟均未考虑隧道直径变化对管线可能产生的影响,在今后的研究中应该加以重视.
[1] 张治国, 黄茂松, 王卫东.隧道开挖对层状地基中邻近管道影响的DCBEM-FEM耦合方法[J].岩土工程学报, 2011, 33(10): 1554-1561.
[2] VORSTER T E B,KLAR A,SOGA K, et al.Estimating the effects of tunneling on existing pipelines [J].Journal of geotechnical and geoenvironmental engineering, 2005, 131(11): 1399-1410.
[3] KLAR A, VORSTER T E B, SOGA K, et al.Soil-pipe-tunnel interaction: comparison between winkler and elastic continuum solutions[J].Geotechnique, 2005, 55(6): 461- 466.
[4] MARSHALL A M, KLAR A, MAIR R J.Tunneling beneath buried pipes: View of soil strain and its effect on pipeline behavior[J].Journal of geotechnical and geoenvironmental engineering, 2010, 136(12): 1664-1672.
[5] 王正兴,缪林昌,王冉冉,等.砂土中隧道施工引起土体内部沉降规律特征的室内模型试验研究[J].土木工程学报, 2014, 47(5): 133-139.
[6] 吴锋波,金淮,尚彦军.城市轨道交通隧道周边地下管道变形预测研究[J].岩石力学与工程学报, 2013, 32(S2): 3592-3601.
[7] 张剑涛,姚爱军,胡愈,等.地铁盾构隧道下穿覆土中雨污管道影响分析[J].中国科技论文在线精品论文, 2016, 9(14):1454-1468.
[8] 郭庆海,刘文,胡群芳,等.盾构施工对沥青路面影响评估[J].郑州大学学报(工学版),2004,25(3):70-73.
[9] 张洵安,王显彬.软岩隧道开挖与支护的三维有限元仿真分析[J].郑州大学学报(工学版),2008,29(2):137-144.
[10] 孙宇坤,吴为义,张土乔.软土地区盾构隧道穿越地下管道引起的管道沉降分析[J].中国铁道科学,2009,30(1):80-85.
[11] 孙海霞,赵文,王钊宇.盾构法施工中地下管道沉降监测与数值模拟[J].沈阳工业大学学报,2010,32(4):454-458.
[12] 林韵梅.实验岩石力学[M].北京: 煤炭工业出版社, 1984.
[13] PRASAD S K.TOWHATA I, CHANDRADHARA G P, et al.Shaking table tests in earthquake geotechnical engineering[J].Current science, 2004, 87(10):1398-1404.
[14] 林皋,朱彤,林蓓.结构动力模型试验的相似技巧[J].大连理工大学学报,2000,40(1):1-8.