0 引言
交叉口是道路交通的咽喉,据统计,车辆通过信号控制交叉口时受信号灯影响被耽误的时间约占总行程时间的31%[1].而交叉口延误可以作为交叉口设施设置与信号配时改善的评价参数,也可以反映驾驶员在交叉口的受阻、耗费等情况.但由于各种因素限制,至今无法实时直接地获取信号交叉口的延误值.因此,国内外研究者对信号交叉口延误参数的获取展开了一系列研究.前期主要对延误推导的模型进行了分析[2-3],目前,国内外一些学者开始对交叉口的延误分布展开探索,Noroozi等[4]对延误分布与高峰小时流量以及HCM计算式的关系进行了分析,Chen等[5]分析了单个车辆以及车均控制延误的分布情况,并定义了延误不确定性系数,对600 s间隔下的参数情况进行了分析.
然而,由于延误参数影响因素的随机性和交叉口环境的复杂性,模型获取的方法对随机性的因素考虑不足,而实时的人工观测则存在不连续性等特点,设置先进的检测设施一方面存在设备设置费用较高的特点,另一方面设施设置的要求也较高.
信号交叉口摄像头的普遍设置为信号交叉口提取前几辆车的延误提供了契机.本文研究以信号交叉口红灯期间第一辆车辆到达分布特性为分析对象,以建立的仿真平台为基础,以正交试验设计为实验优化方法,对各种影响因素下的车辆到达特征进行了研究,本文研究成果为实时准确地获取红灯期间第一辆车的到达-离去时间差值及相关研究提供了基础,进一步为分析交叉口进口道的延误提供了一种思路,对实现信号交叉口配时方案设计与优化及交叉口服务水平评价等提供了一种更可靠的方案.
1 数据采集
本研究以安装有摄像头的信号交叉口为研究背景,由前期以及其他学者的研究可知,车辆进入进口道后,可以得到前几辆车的到达及离开时间[6].考虑到第一辆车的停车及启动时间与进口道延误有较紧密的关系,结合摄像头安装背景下的车辆信息获取情况,笔者以每个信号周期第一辆停止在停车线前的车为研究对象,以信号交叉口红灯启亮时刻作为信号周期开始的时间,则第一辆车到达时间界定为红灯启亮与第一辆车进入进口道并在停车线前停止的时间差值.
综合考虑可观测地点的选取和可用的观测方法,笔者对于数据的获取通过人工提取的方式得到,即通过现场设置摄像机拍摄视频,视频同时拍摄到车辆到达及信号灯的灯色情况,后期通过人工对视频进行逐帧观测提取了车辆到达及信号灯转变时间等需要的参数.考虑到架设的摄像机需要同时拍摄到红灯启亮的时间以及第一辆车的停车时间等信息,通过筛选初步选定地点后,最终通过现场核实选择了重庆市南岸区学府大道与重庆交通大学三号门前的信号交叉口(称为第1信号交叉口)以及重庆市南岸区渝南分流道与民主新街交叉口(称为第2信号交叉口)作为视频拍摄及参数提取的观测地点.
所调查的第1信号交叉口的进口道与上游交叉口的间距接近1 000 m,观测时段所涉及的进口道饱和度范围为0.43~0.8,大车率为8%~13%;而观测的第2信号交叉口与上游交叉口的间距也超过了1 000 m,所调查的进口道饱和度范围为0.27~0.85,大车率为11%~ 25%.
后期通过人工观测对第一辆车的到达时间进行了提取.得到第1信号交叉口的第一辆车到达时间的有效周期为260个.第2信号交叉口的第一辆车到达时间的有效周期为45个.第1信号交叉口观测相位的红灯时长为30 s,经统计,该交叉口红灯期间第一辆车到达的时间分布均值为14.17 s,到达时间最大值为30 s,最小值为0 s,即平均到达时间为接近红灯一半的时间,最大到达时间为红灯即将结束的时间车辆刚好到达停车线并停车,而最小的时间对应的场景为红灯启亮的瞬间.第2信号交叉口观测相位的红灯时长为70 s,经统计,该交叉口红灯期间第一辆车到达时间的均值为11.89 s,到达时间最大值为37 s,最小值为1 s.
2 车辆到达分布拟合
对第一辆车到达的时间情况进行了拟合,拟合效果图如图1和图2所示.
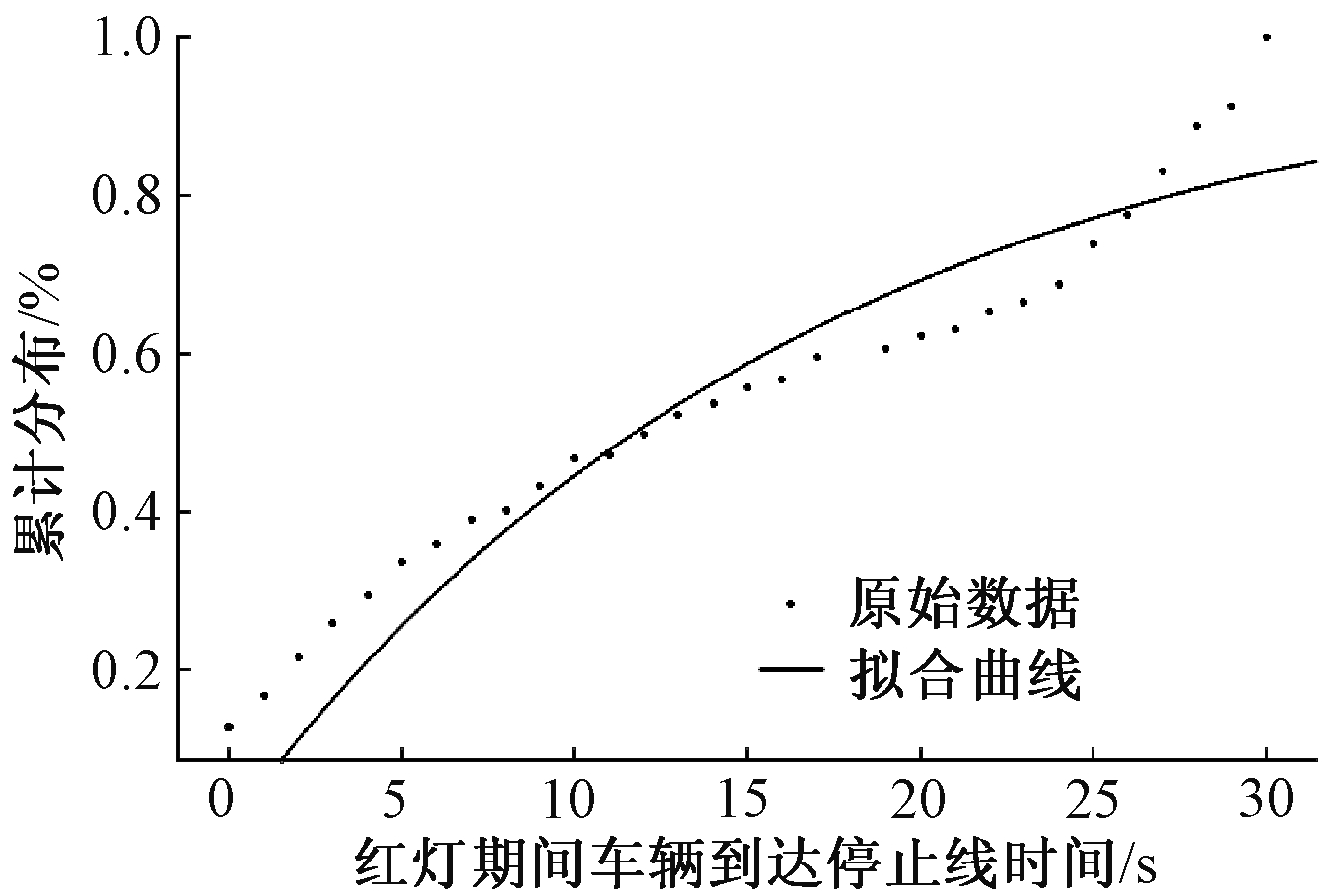
图1 第1信号交叉口第一辆车到达时间拟合结果
Fig.1 Fitting result of the time difference between red time and the first vehicle′s arriving time at the No. 1 intersection
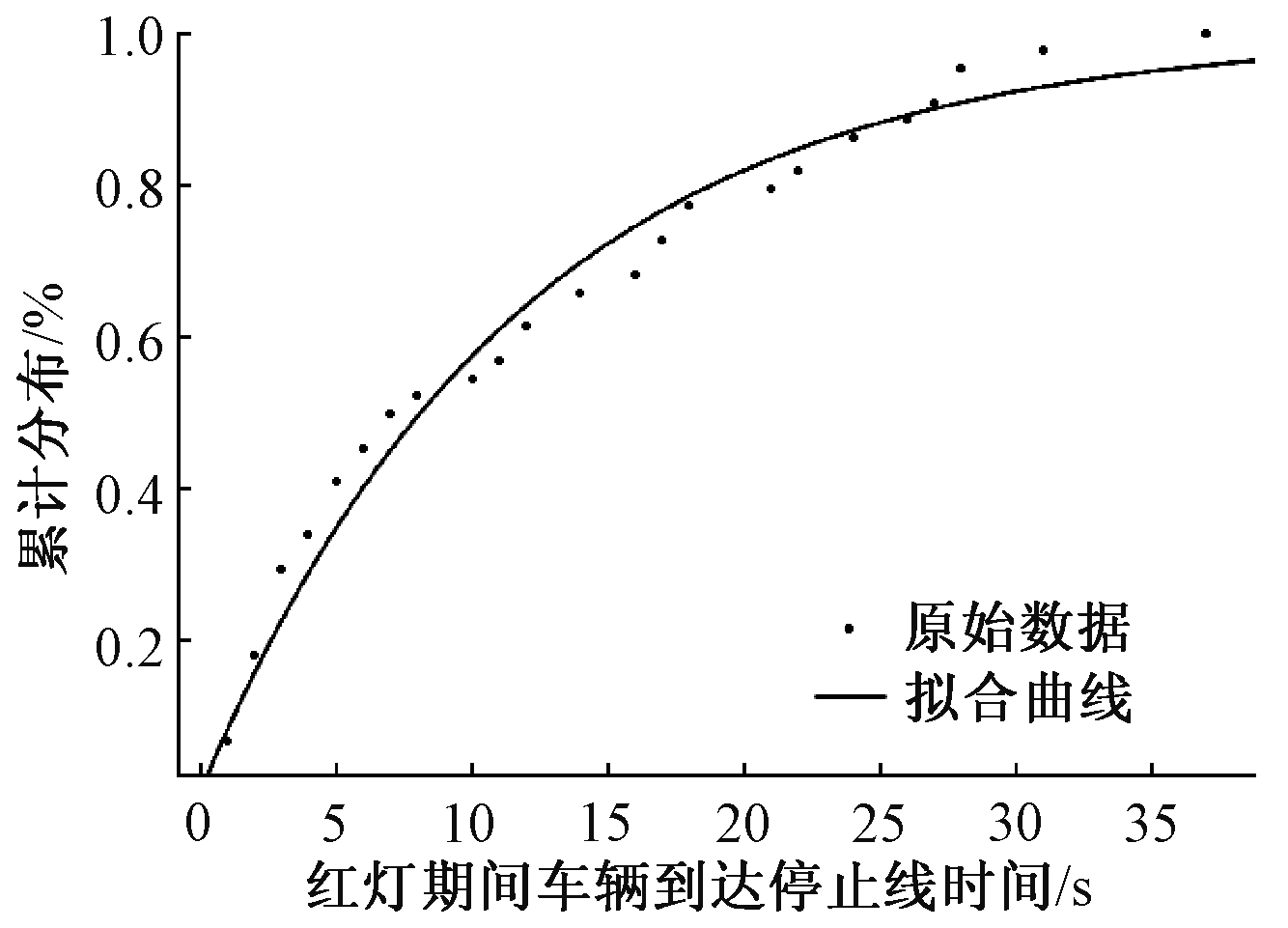
图2 第2信号交叉口第一辆车到达时间拟合结果
Fig.2 Fitting result of the time difference between red time and the first vehicle′s arriving time at the No. 2 intersection
由图1和图2可以看出,每个周期的第一辆车到达时间分布服从泊松分布,且分布模型可以拟合为:
f(x)=1-exp(-x/b).
(1)
式中:f(x)指红灯启亮与第一辆车到达时间的差值小于等于x的概率;b为待估参数.
由上述提取的数据进行拟合,得到第1信号交叉口系数b的拟合结果为16.89,95%置信区间(15.39,18.38),拟合优度结果为0.072 72,R2为0.891 7,表明拟合效果好.第2信号交叉口系数b拟合结果为12.14,95%置信区间(11.36,12.91),拟合优度结果为0.042 85,R2为0.972 2.
3 正交试验设计
通过对调查的两个交叉口车辆到达时间进行分析,得到在饱和度较低的情况下,第一辆车的到达时间相对较长,而在饱和度相对较高的情况下,第一辆车的到达时间相对较短.结合现场的观测及车辆在上下游交叉口间行驶特征的分析,参考相关指南文献[7]等,信号交叉口与上游交叉口是否采用协调控制以及上下游交叉口间车辆行驶的速度主要对信号交叉口不同信号期间的车辆到达类型等产生影响;而上游交叉口的形式等其他因素的影响可以化解为下游进口道的饱和度、车辆到达类型等因素.考虑到上游及其他方向大车混入情况、交叉口距离等均可能会对第一辆车的到达时间产生影响,因此本部分对可能影响第一辆车到达的因素进行分析,并对试验进行了设计.综合上述分析,论文主要考虑了车辆到达类型、交叉口间距、进口道饱和度、饱和流量、绿信比以及大车比例等因素对第一辆车到达分布的影响.具体因素的设置情况为:
(1)车辆到达类型.对于车辆到达类型,参考文献[7],车辆的到达类型可以分为五类,分别为:超过80%的车辆在红灯期间到达;有40%~80%的车辆在红灯期间到达;随机到达,即该交叉口受其他交叉口影响较小;有40%~80%的车辆在绿灯期间到达;有超过80%的车辆在绿灯期间到达[8].本次分析也选取这5类作为车辆到达类型的分析水平.
(2)交叉口间距.交叉口间距对上游车辆行驶的离散型有较大的影响,如车辆成队列到达或者随机到达.参考相关的研究成果[9],研究中对于交叉口间距的选择区段分别为<150~≤300 m、<300~≤450 m、<450~≤600 m、<600~≤800 m、大于800 m等5个等级.
(3)进口道饱和度.进口道饱和度与交叉口延误之间有着较紧密的关系,且可能会影响第一辆车到达的情况.结合交通场景中的低饱和度、中等饱和、接近饱和以及过饱和,考虑水平的分析情况.研究中将进口道饱和度分为5级,分别为:饱和度小于0.25,[0.25,0.5),[0.5,0.75),[0.75,1),≥1等情况.
(4)饱和流量.饱和流量能够反映道路的通行能力,将直接影响饱和度的大小,进而会对第一辆车的到达情况产生影响.参考相关文献[9-11],将饱和流量分为以下5级:1 500、1 600、1 650、1 750、1 800 pcu·h-1.
(5)绿信比.绿信比决定车辆的通行权,也会对第一辆车的到达情况产生影响.参考Piotr等的研究结果[12-13],将绿信比分为以下5级:0.2、0.3、0.4、0.5、0.6.
(6)大车比例.由于大车的体积较大,在行驶中所占用的空间也较大,而且大车的启动时间较长,行驶速度也较慢,所以大车对道路交通的影响较大,对第一辆车的到达情况也可能会产生影响.结合目前城市道路的实际情况,对于大车率分为≤5%,<5%~≤10%,10%~≤25%,25%~≤40%,>40%.
上述6个因素,均为5个水平,如果逐个情况考虑,需要15 625次试验,试验次数太大.另外,所考虑的各因素之间可能存在交互影响的情况,且上述6个因素中,影响车辆到达的程度也不能确定.实验优化设计可以在较少的试验场景下获取较佳的效果.正交试验的试验方案是有代表性的,且能够比较全面地反映各因素水平指标影响的大致情况.因此,对各种情况下的第一辆车的到达时间进行分析,使用正交试验来优化实验方案的设置,此次共设置25种试验方案,详细方案设置如表1所示.
4 仿真分析
为了对各种因素影响下的第一辆车到达时间分布进行分析,鉴于实际数据获取的场景较难实现,研究中通过构筑仿真平台对第一辆车的到达分布影响因素进行了分析.研究以实际调查的第1信号交叉口调查得到的大车及小车车辆速度作为标定数据,在微观仿真软件VISSIM中构筑了上述25种实验场景.构建的部分仿真场景如图3.

图3 部分仿真试验场景构筑界面
Fig.3 Parts of the simulation scenar of building interface
如图3所示,通过构筑的仿真场景,提取车辆的运行轨迹和信号控制周期,即可得出所要分析的第一辆车的到达情况.
表1 正交试验场景下的时间差值及直观分析
Tab.1 time difference and intuitive analysis of the orthogonal experiment simulation
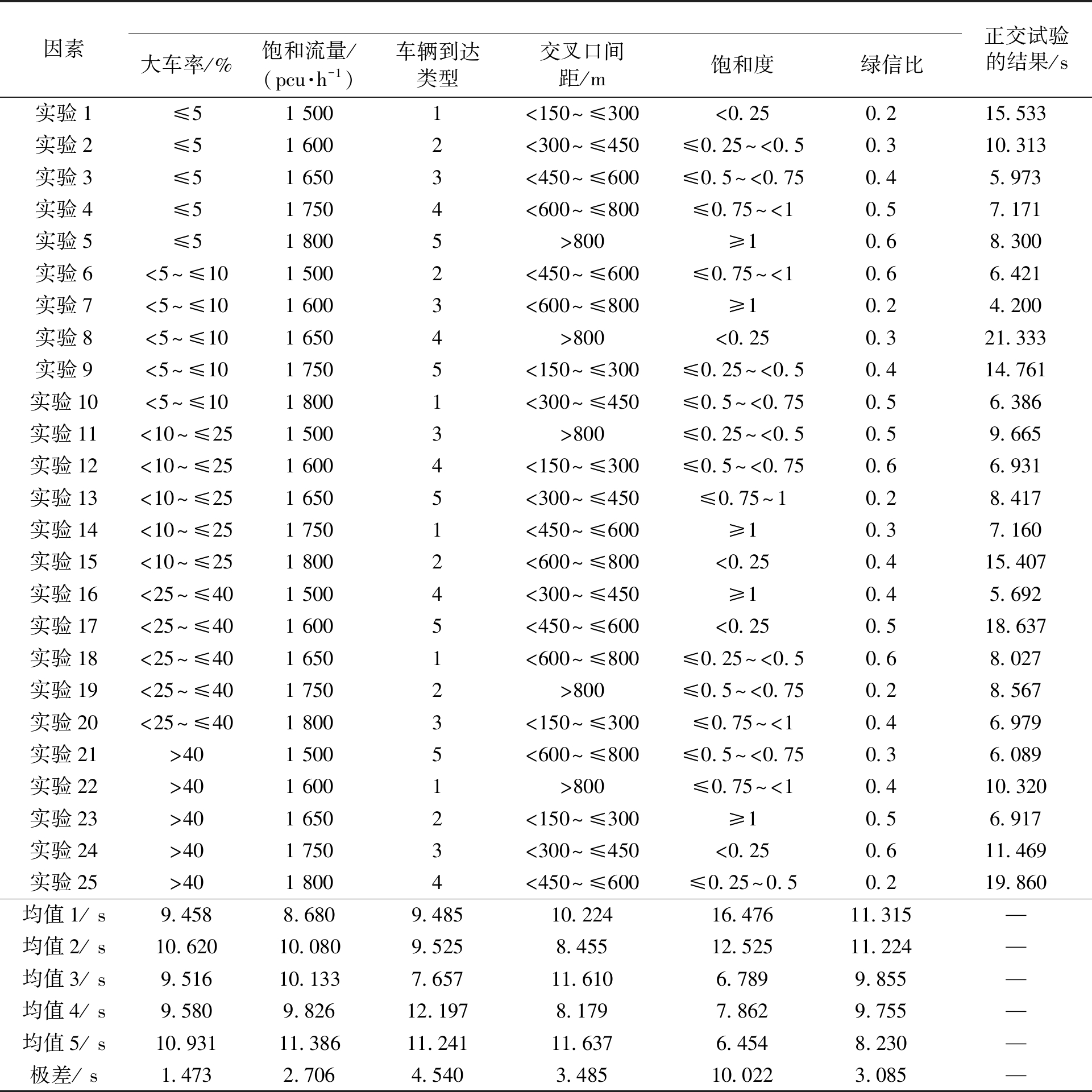
因素大车率/%饱和流量/(pcu·h-1)车辆到达类型交叉口间距/m饱和度绿信比正交试验的结果/s实验1≤51 5001<150~≤300<0.250.215.533实验2≤51 6002<300~≤450≤0.25~<0.50.310.313实验3≤51 6503<450~≤600≤0.5~<0.750.45.973实验4≤51 7504<600~≤800≤0.75~<10.57.171实验5≤51 8005>800≥10.68.300实验6<5~≤101 5002<450~≤600≤0.75~<10.66.421实验7<5~≤101 6003<600~≤800≥10.24.200实验8<5~≤101 6504>800<0.250.321.333实验9<5~≤101 7505<150~≤300≤0.25~<0.50.414.761实验10<5~≤101 8001<300~≤450≤0.5~<0.750.56.386实验11<10~≤251 5003>800≤0.25~<0.50.59.665实验12<10~≤251 6004<150~≤300≤0.5~<0.750.66.931实验13<10~≤251 6505<300~≤450≤0.75~10.28.417实验14<10~≤251 7501<450~≤600≥10.37.160实验15<10~≤251 8002<600~≤800<0.250.415.407实验16<25~≤401 5004<300~≤450≥10.45.692实验17<25~≤401 6005<450~≤600<0.250.518.637实验18<25~≤401 6501<600~≤800≤0.25~<0.50.68.027实验19<25~≤401 7502>800≤0.5~<0.750.28.567实验20<25~≤401 8003<150~≤300≤0.75~<10.46.979实验21>401 5005<600~≤800≤0.5~<0.750.36.089实验22>401 6001>800≤0.75~<10.410.320实验23>401 6502<150~≤300≥10.56.917实验24>401 7503<300~≤450<0.250.611.469实验25>401 8004<450~≤600≤0.25~0.50.219.860均值1/ s9.4588.6809.48510.22416.47611.315—均值2/ s10.62010.0809.5258.45512.52511.224—均值3/ s9.51610.1337.65711.6106.7899.855—均值4/ s9.5809.82612.1978.1797.8629.755—均值5/ s10.93111.38611.24111.6376.4548.230—极差/ s1.4732.7064.5403.48510.0223.085—
将仿真场景得到的各种试验下的第一辆车平均到达时间使用正交试验的方法进行分析,得出各试验场景下的分布参数.
正交试验分析过程如下:假设Kij为第j列因素第i水平下所有试验结果之和,如K12=Y1+Y5+Y9+Y13(Yi表示试验号为i的试验结果,i=1,2,…,16);ωij为第j列因素第i水平的试验指标的平均值,即 ωij=Kij/4;Rj为极差,即ωij中的最大值减去最小值,Rj=(ωij)max - (ωij)min[14].
所得到的25种试验场景下红灯期间到达信号交叉口第一辆车的到达时间及不同影响因素在各水平下的第一辆车的到达时间的结果分析如表1所示.
由表1最后一行可以看出,各因素中极值大小的分布为: R饱和度>R车辆到达类型>R交叉口间距>R绿信比>R饱和流量>R大车率,表明饱和度对交叉口车辆到达的影响最大,大车率对交叉口车辆到达的影响最小.各因素对交叉口车辆到达的影响程度由大到小依次为:饱和度>车辆到达类型>交叉口间距>绿信比>饱和流量>大车率.
图4的曲线表示各影响因素在上述五个水平下的试验指标第一辆车的到达时间的平均值.由图4中各曲线的上升及转折情况可以看出,大车率从5%增加到<5%~≤10%的时候时间差有所增加;从<5%~≤10%增加到<10%~≤25%的时候时间差减少;从<10%~≤25%到<25%~≤40%时,时间差基本一致;从<25%~≤40%增加到40%以上时,时间差减少;饱和流量从1 500 pcu·h-1增加至1 600 pcu·h-1,时间差有所增加,在<1 600~≤1 750 pcu·h-1处,时间差基本一致;车辆到达类型为随机到达时时间差最小,车辆到达类型为40%~80%的车辆在绿灯期间到达交叉口时,时间差最大;交叉口间距对时间差影响较为显著,但是没有一定规律;饱和度从≤0.25~<0.5时,时间差明显减少,从≤0.5~<0.75时,时间差稍稍增加,从≤0.75~<1增加到1及以上时,时间差减少,可以看出饱和度对车辆到达类型有显著影响;绿信比从0.2增加到0.6时,时间差呈递减状.
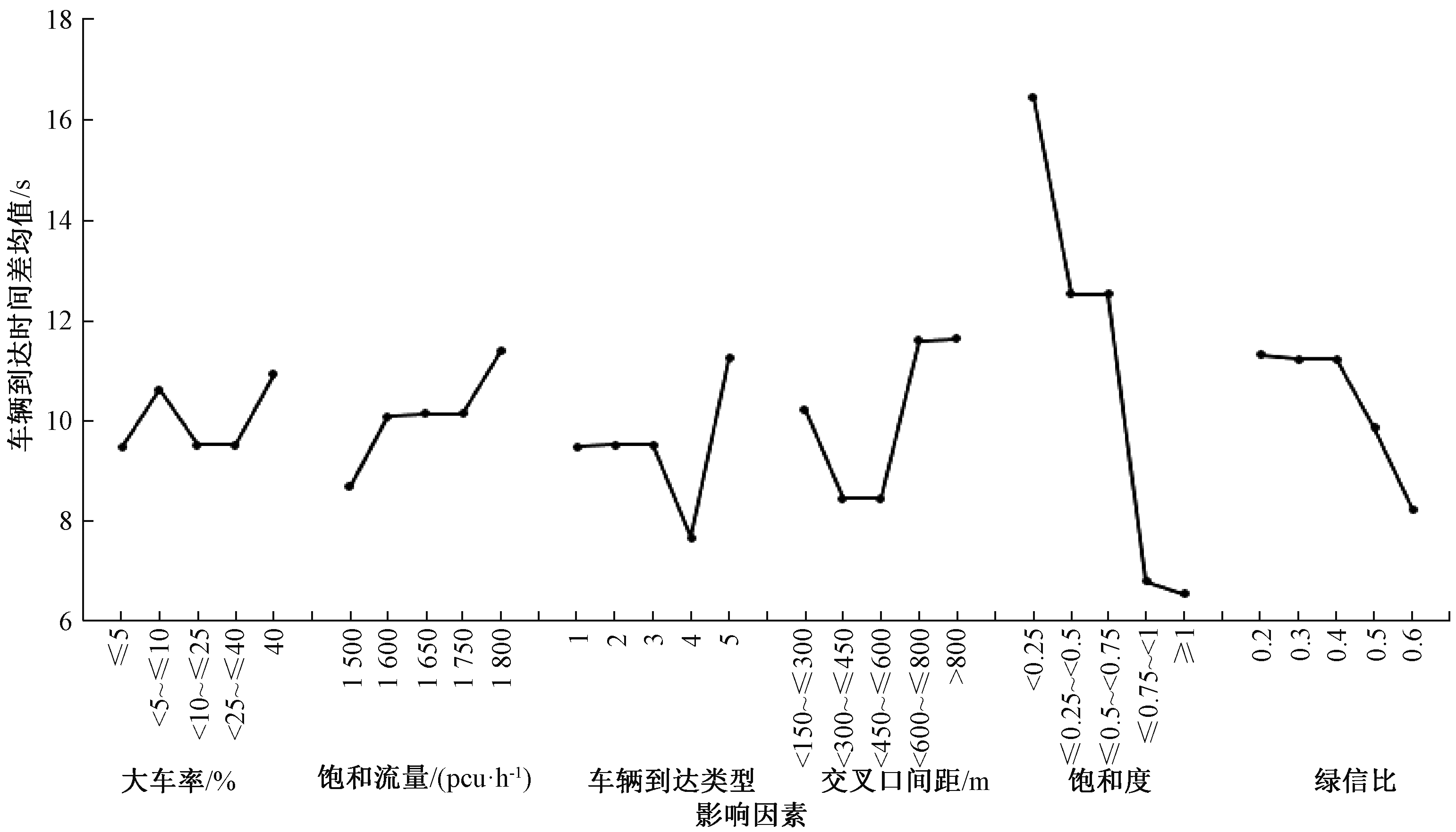
图4 正交试验效应曲线
Fig.4 The response curve of the orthogonal experiment simulation
由于饱和流量和饱和度会对时间差产生交互作用,使用交互作用表进行分析,交互作用的数值根据表1对应的饱和流量和饱和度下的第一辆车到达时间的正交试验结果得到.如当饱和度<0.25、饱和流量为1 500 pcu·h-1时,表1对应的第一辆车到达时间的正交试验结果为15.333 s,即为表2中饱和度<0.25、饱和流量为1 500 pcu·h-1时的交互作用数值.详细交互作用如表2所示.
表2 饱和流量和饱和度交互作用
Tab.2 The interactive table of the saturation and saturated flow s
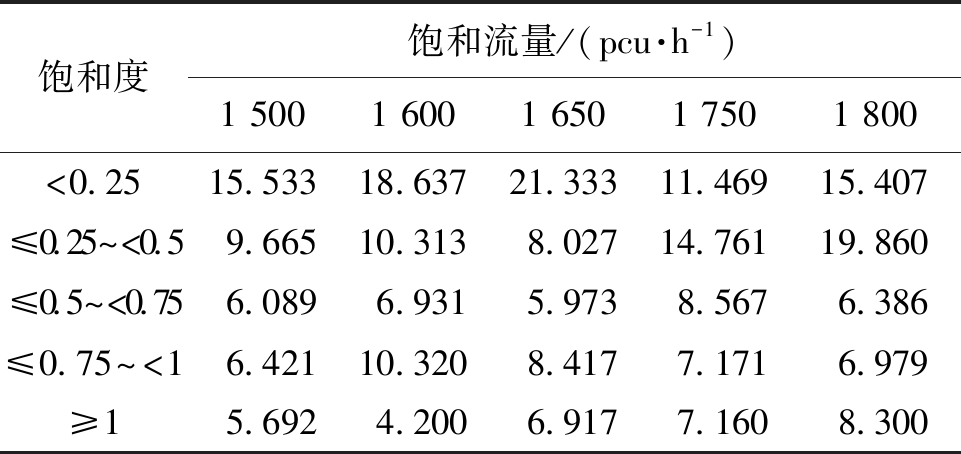
饱和度饱和流量/(pcu·h-1)1 5001 6001 6501 7501 800<0.2515.53318.63721.33311.46915.407 ≤0.25~<0.59.66510.3138.02714.76119.860 ≤0.5~<0.756.0896.9315.9738.5676.386 ≤0.75~<16.42110.3208.4177.1716.979 ≥15.6924.2006.9177.1608.300
由表2可以看出,在饱和流量为1 650 pcu·h-1,且饱和度<0.25时,该交互作用的值达到最大,为21.333 s,说明在该交互作用下,对车辆到达的影响程度最高.
5 结论
第一辆车的到达情况与延误参数之间有紧密的关联关系,主要对红灯期间第一辆车的相关特征进行了分析.研究结论主要有:
(1)通过2个信号交叉口的信号转换以及车辆到达进行提取和分析,拟合了第一辆车到达交叉口的函数.
(2)对可能影响车辆到达的因素进行了选取,最终选择车辆到达类型、交叉口间距、进口道饱和度、饱和流量、绿信比、大车率等作为可能影响车辆到达的因素,并通过正交试验设置了优化试验方案.
(3)通过微观仿真平台,对正交试验构筑的场景进行了分析,最终得到了影响车辆到达的因素排序依次为饱和度、车辆到达类型、交叉口间距、绿信比、饱和流量、大车率.在饱和流量为1 650 pcu·h-1,且饱和度<0.25时,对车辆到达的影响程度最高.
(4)对第一辆车到达特征与其他参数的关联分析将是本项目后续研究的主要方向.
[1] 马天宇.信号交叉口倒计时显示屏对驾驶员行为影响分析[D].长春:吉林大学交通学院,2008.
[2] WEBSTER F V. Traffic signal settings[R]. Road Research Technical Paper No.39, Road Research Laboratory. Her Majesty Stationary Office,London,UK.1958.
[3] AKCFLIK I, ROUPHAIL N. Overflow of queues and delays with random and platooned arrivals at signalized intersections [J]. Journal of advanced transportation, 1994, 28(3):227-251.
[4] NOROOZI R, HELLINGA B. Distribution of delay in signalized intersections: day-to-day variability in peak-hour volumes [J]. Journal of transportation engineering, 2012, 138(9):1123-1132.
[5] CHEN P, ZHENG F F, LU G Q, et al. Comparison of variability of individual vehicle delay and average control delay at signalized intersections [J].Transportation research record, 2016,2553:128-137.
[6] 张惠玲,李克平,敖谷昌. 监控环境下信号交叉口控制延误的获取方法[J].北京交通大学学报,2010,34(6):40-45.
[7] Transportation Research Board. Highway capacity manual 2010[R].Washington D C: National Research Council, 2010.
[8] 李志.平面交叉口间距对道路交通的影响[J].山西建筑,2014,40(26):157-159.
[9] 吴兵,李晔.交通管理与控制[M].北京:人民交通出版社,2009.
[10] 陈锦秀, 陈小鸿, 林航飞. 《城市道路平面交叉口规划与设计规程》基本饱和流量与大车校正系数检验研究[J].城市交通,2004,2(3):17-20.
[11] 沈家军,王群. 基于通行效率最优的交叉口控制方式优选[J].郑州大学学报(工学版), 2016,37(3):60-63.
[12] OLSZEWSKI P S. Modeling probability distribution of delay at signalized intersections[J].Journal of advanced transportation, 1994,28(3):253-274.
[13] 董海龙,汤旻安,程海鹏. 非均衡交通流五岔路口交通信号智能控制研究[J].郑州大学学报(工学版), 2017,38(1):68-73.
[14] ADESOLA O I. Orthogonal experiments in the develo-pment of carbon-resin for chloride removal from solutions [J].Statistical methodology, 2009, 6 (2):109-119.