0 引言
滚动轴承的运行状态良好与否将直接影响机械系统的可靠性和使用寿命,准确地判断出滚动轴承的运行状态将在很大程度上避免事故发生,因此对滚动轴承进行状态识别具有重要意义[1].
近年来,由压缩感知发展而来的基于稀疏编码的模式识别方法已广泛应用于图像识别、语音识别等相关领域.在国外,Wright等[2]首先将稀疏编码应用于模式识别,其提出的稀疏表征分类(sparse representation classification, SRC)方法经验证是一种有效的人脸识别方法.Yang等[3]在SRC方法的基础上进行了相关改进,提出了Metaface方法,分别对每类样本学习一组字典,大大缩小了字典规模,提高了SRC的识别效率.稀疏编码是一种自适应好、稳定性高的机器学习方法[4],近年来国内一些研究人员已尝试将其应用于旋转机械的故障识别,并提出了一些有效的故障识别方法,降低了故障诊断的工作难度.Liu等[5]利用移不变稀疏编码(SISC)对信号进行字典学习,从而解决了时域信号分割所造成的特征时移问题,并利用LDA分类器对所提取的稀疏特征进行模式识别,取得了较优异的效果,但是该方法所需的计算量非常大,在处理海量冗余数据方面具有一定的局限性.朱会杰等[6]利用频域信号进行字典学习,且利用计算效率更高的稀疏编码对滚动轴承进行状态识别,该方法既解决了时域信号特征时移问题,又提高了识别效率和准确率.但由于该方法仅将单通道信号作为训练样本进行字典学习,存在信息利用不全面等问题,所构造字典的鲁棒性有待进一步提高.
基于以上分析,笔者提出一种结合全矢谱和稀疏编码的滚动轴承故障识别方法.首先利用全矢谱技术对训练样本进行信息融合.然后,利用全矢融合后的主振矢信号构造自适应字典,从而避免了信息遗漏问题,由于主振矢信号属于频域信号,因此也不会出现特征时移现象.最后,利用稀疏编码对滚动轴承各类信号进行状态识别.
1 全矢谱与稀疏编码理论
1.1 全矢谱理论
在各谐波频率组合作用下,转子的涡动轨迹为一系列椭圆.全矢谱技术定义上述椭圆的长轴和短轴分别为主振矢和副振矢,将其作为评价转子振动强度的指标和故障诊断的依据.
设x,y方向上的离散信号分别为{xn}和{yn},将其融合为复序列,即
{zn}={xn}+j{yn}.
(1)
对{zn}做傅里叶变换得到{Zn},由傅里叶变换的共轭性可得到:
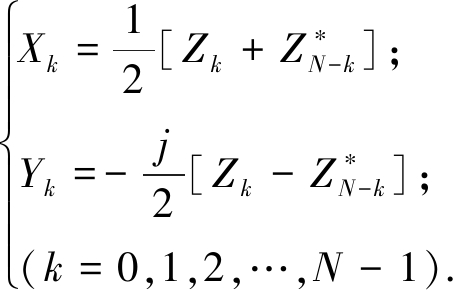
(2)
再根据傅里叶变换性质可得下式(具体推导过程参考文献[7]):
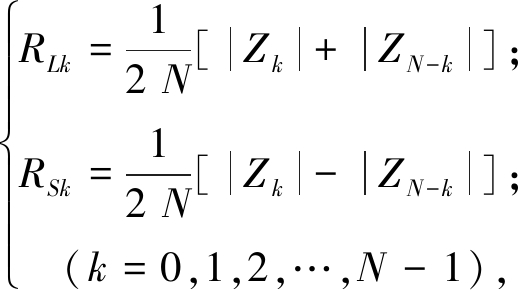
(3)
式中:RLk为主振矢;RSk为副振矢.
全矢谱在算法上结构稳定,且与单通道分析方法兼容,可满足实际诊断要求.
1.2 稀疏编码模型
稀疏编码源自生物神经学,旨在以最高效的编码方式最大程度地反映信号的特征信息.稀疏编码的数学模型可表示为:
(4)
式中:X∈RM×T为一个输入信号;D∈RM×K为过完备字典;dk为字典中的基函数;s为信号X的稀疏表征系数;ε一般为高斯白噪声.
在式(4)所示模型中,信号X的维数应小于基函数dk的个数,即M<K,且在大部分情况下M≪K,即字典D为过完备字典.这是由于稀疏编码模型旨在求X的稀疏解,而D若为满秩矩阵则将不满足要求.
通常采用l0范数的大小来表征稀疏性,因此稀疏编码的过程可转化为求解下式:
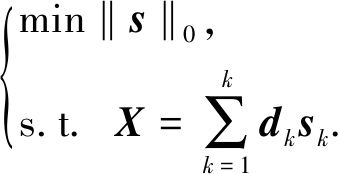
(5)
1.3 自适应字典学习
字典学习是稀疏编码中的重要部分,主要包括固定字典和自适应字典[8].其中自适应字典能根据不同类型的信号自适应地产生最能匹配信号内在结构的基函数库.
采用K-SVD算法构造自适应字典,该算法灵活性好、匹配精度高,主要步骤如下:
(1)依次将样本信号以列向量赋值给字典矩阵,构造初始字典D;
(2)根据上述稀疏编码模型,求解稀疏系数s;
(3)更新字典.该计算步骤等同于求解以下问题:
![]() ∀i,‖si‖0≤T0,
∀i,‖si‖0≤T0,
(6)
式中:T0为稀疏编码中对应基函数上限,即稀疏度.
2 全矢稀疏编码模式识别原理
2.1 基于全矢谱的模式识别机理
将一段较长的时域信号分割为若干信号段来进行分析是一种常见的信号处理方法.然而,由于时域信号中的特征位置分布具有随机性,因此其中的特征模式会因信号分割而被移动,从而造成特征时移现象[9].图1为不同状态下滚动轴承两个方向的时域振动信号.
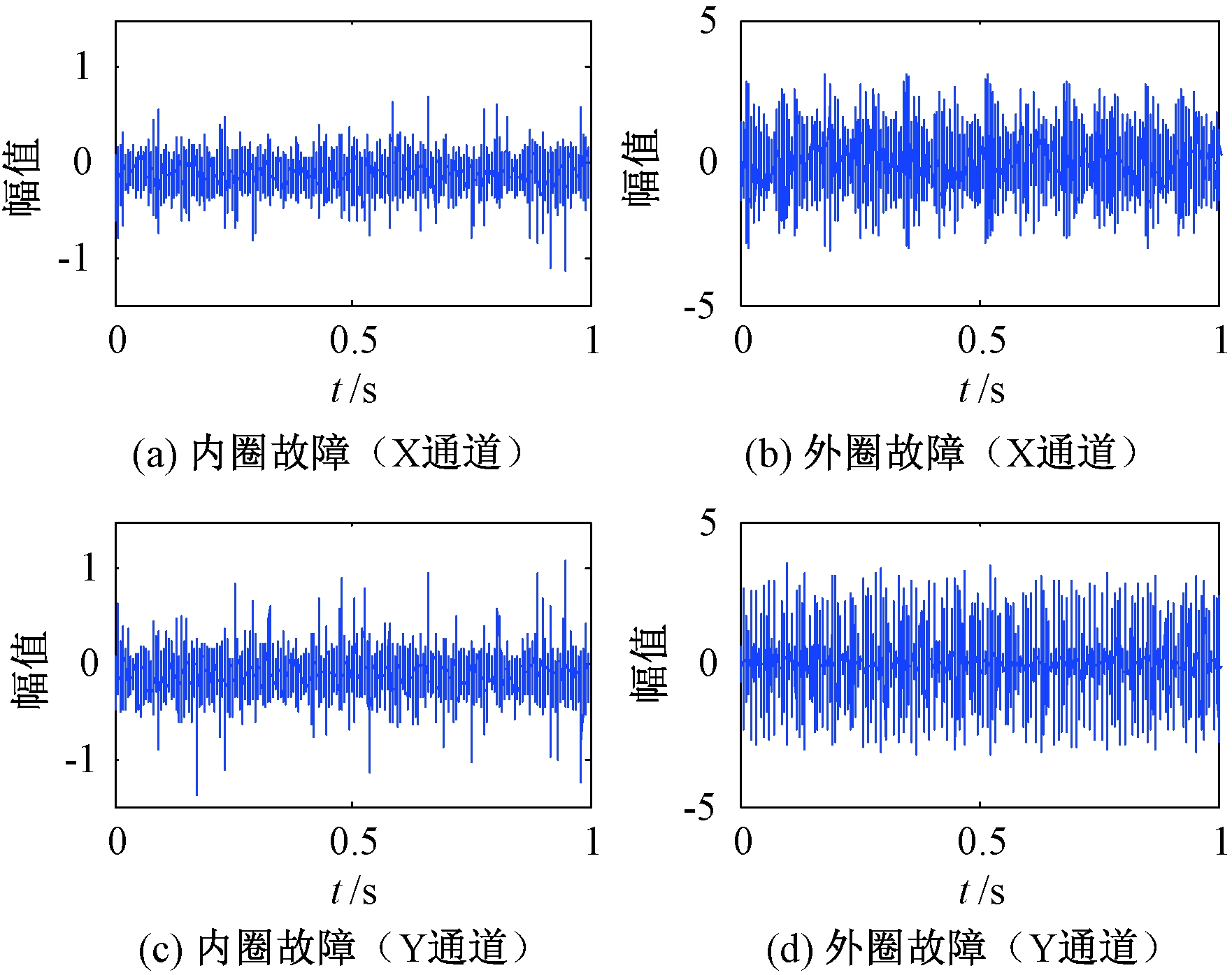
图1 不同状态下的轴承时域信号
Fig.1 Bearing time domain signals under different status
由图1可知,当滚动轴承处于不同运行状态时,其时域信号差异明显.且当其运行状态相同时,由于信号采集位置及截取起点的不同,其时域信号也具有差异.因此,基于时间序列对相同状态下的信号进行稀疏编码不能保证其特征模式相同.
文献[6]利用单通道实际信号验证了当滚动轴承处于不同状态时,其频谱之间具有很大差异,因此无法互相稀疏表征.而当滚动轴承处于相同状态时,其频谱的统计规律相似,因此可相互稀疏表征.
然而,对于同一截面上的同源振动信号,当传感器布置的方向不同时,所采集到的信号之间往往存在差异.图2为上述时域信号对应的频谱和将其进行全矢融合后的主振矢谱.
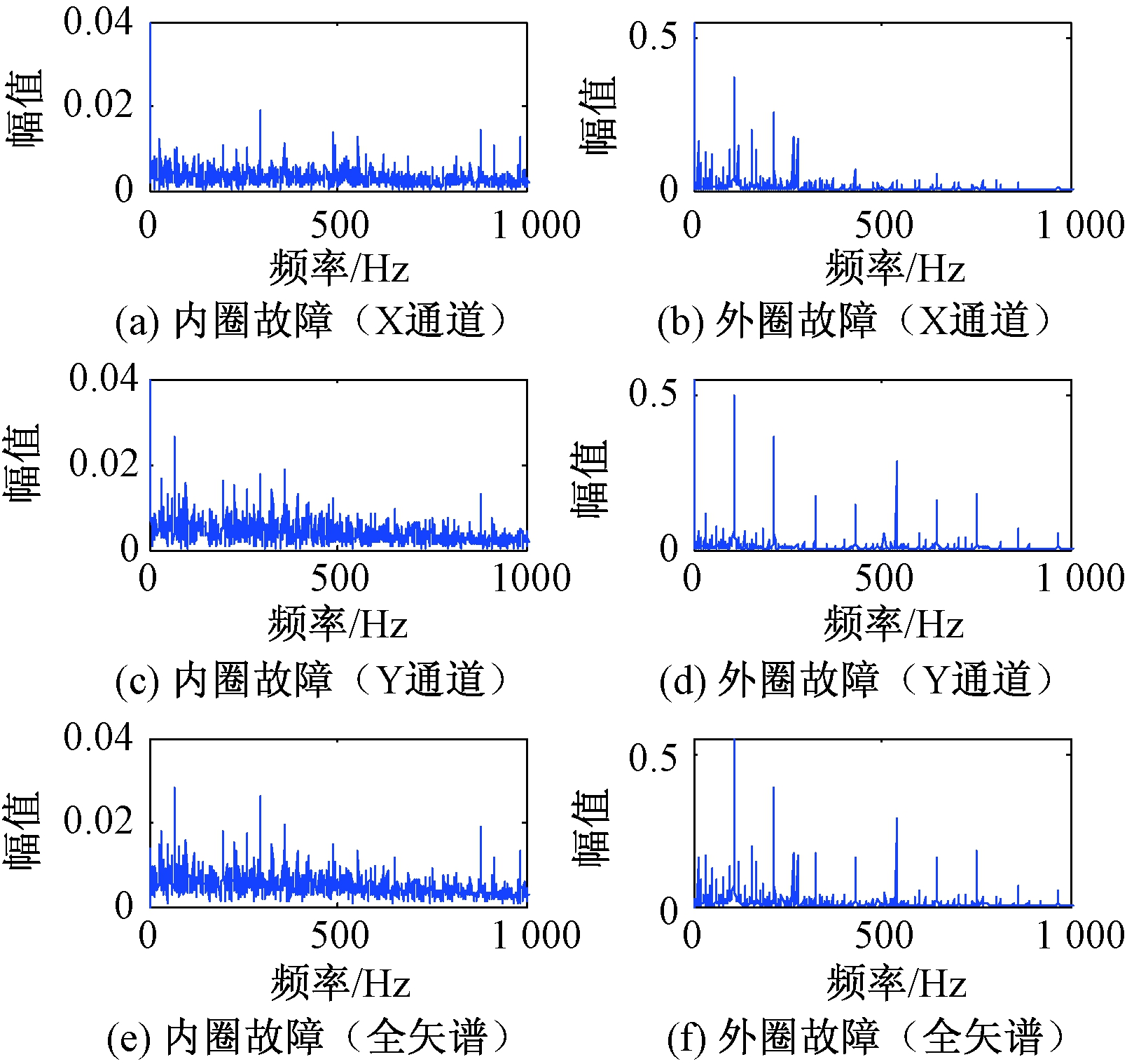
图2 不同状态下的轴承频谱及全矢谱
Fig.2 Bearing frequency spectrum and full vector spectrum under different status
由图2可知,不同通道的同源信号的频谱结构差别明显,因此相互稀疏表征的效果将会较差.而图2(e)和图2(f)所示的主振矢谱有效地融合了两个通道的频率特征信息,因此可以更好地实现频谱的相互稀疏表征,避免了信息缺失问题的出现.
由上述可知,将两个方向的时域样本信号进行全矢融合后得到其主振矢谱,可更好地利用稀疏编码对样本信号进行状态识别.
2.2 基于稀疏重构误差的模式识别原理
由式(6)可知:当稀疏度T0(稀疏编码的基函数个数)确定时,采用由字典学习算法得到的字典D对原信号X进行重构,可得到最小的重构误差,即
![]() ∀i,‖si‖0≤T0,
∀i,‖si‖0≤T0,
(7)
式中:l为不符合稀疏编码条件的字典的编号,l∈(0,n).
由上述分析可知,当样本信号X与字典D所对应的状态一致时,该字典D符合稀疏编码的模型成立条件,即该样本信号X可在已指定的稀疏度T0下很好地被稀疏重构,且其重构误差将会很小.由于不同状态下的主振矢信号之间具有明显差异,则其各自由字典学习算法得到的字典也将差别显著.因此,当样本信号X与当前字典Dl所对应的状态不同时,字典Dl将不适用于对样本信号X进行稀疏编码,即样本信号X在理论上无法在稀疏度T0下很好地被稀疏重构,其重构误差将会明显较大,即
![]() ∀i,‖si‖0≤T0,
∀i,‖si‖0≤T0,
(8)
式中:ε0为稀疏编码的误差限.
因此,可根据上述稀疏编码的特点进行状态识别,为了便于对比,将与样本之间具有最小重构误差率的字典类别作为该样本的状态.稀疏编码的重构误差率表示为:
(9)
基于全矢稀疏编码的滚动轴承模式识别方法主要步骤如下:
(1)利用全矢谱技术对滚动轴承同源双通道信号进行融合,把得到的主振矢信号作为训练样本;
(2)分别对处于每类状态下的主振矢信号进行字典学习,以构造各类状态下所对应的子字典,则所有子字典构成了一个大的基函数库;
(3)确定稀疏编码中的稀疏度T0,利用已构造的各类子字典以相同的稀疏度分别对样本信号进行稀疏编码,得到该样本在各类子字典下进行稀疏编码后的重构信号;
(4)按照式(12)所示计算样本信号和各子字典重构信号之间的重构误差率,当样本与子字典的类别相同时,所得的重构误差率将会很小,且明显小于使用其他子字典重构时所得的误差率.将所得误差率最小的子字典的类别作为该样本的状态类别.
3 实验与分析
本实验采用美国辛辛那提大学智能维护中心提供的滚动轴承数据进行分析.该实验装置如图3所示,其主轴上安装有4个轴承,实验装置中的传动轴由一个直流电机驱动,电动机的转速约为2 000 r/min,转轴和轴承上通过弹性系统施加径向载荷为6 000磅,并且所有轴承都得到了充分润滑.轴承参数如表1所示.在实验中,每个轴承座安装有两个美国PCB公司生产的353B33型ICP加速度传感器(相互垂直布置:一个水平方向,一个垂直方向),因此所采集到的信号属于同源双通道信号,可满足全矢谱融合的基本条件.采样频率为20 000 Hz,每10 min记录一组数据,每组数据共有20 480个点.
表1 实验轴承参数
Tab.1 Experimental bearing parameters

轴承型号滚子个数滚子直径/mm节圆直径/mm接触角/(°)ZA-2115双列轴承168.471.515.17
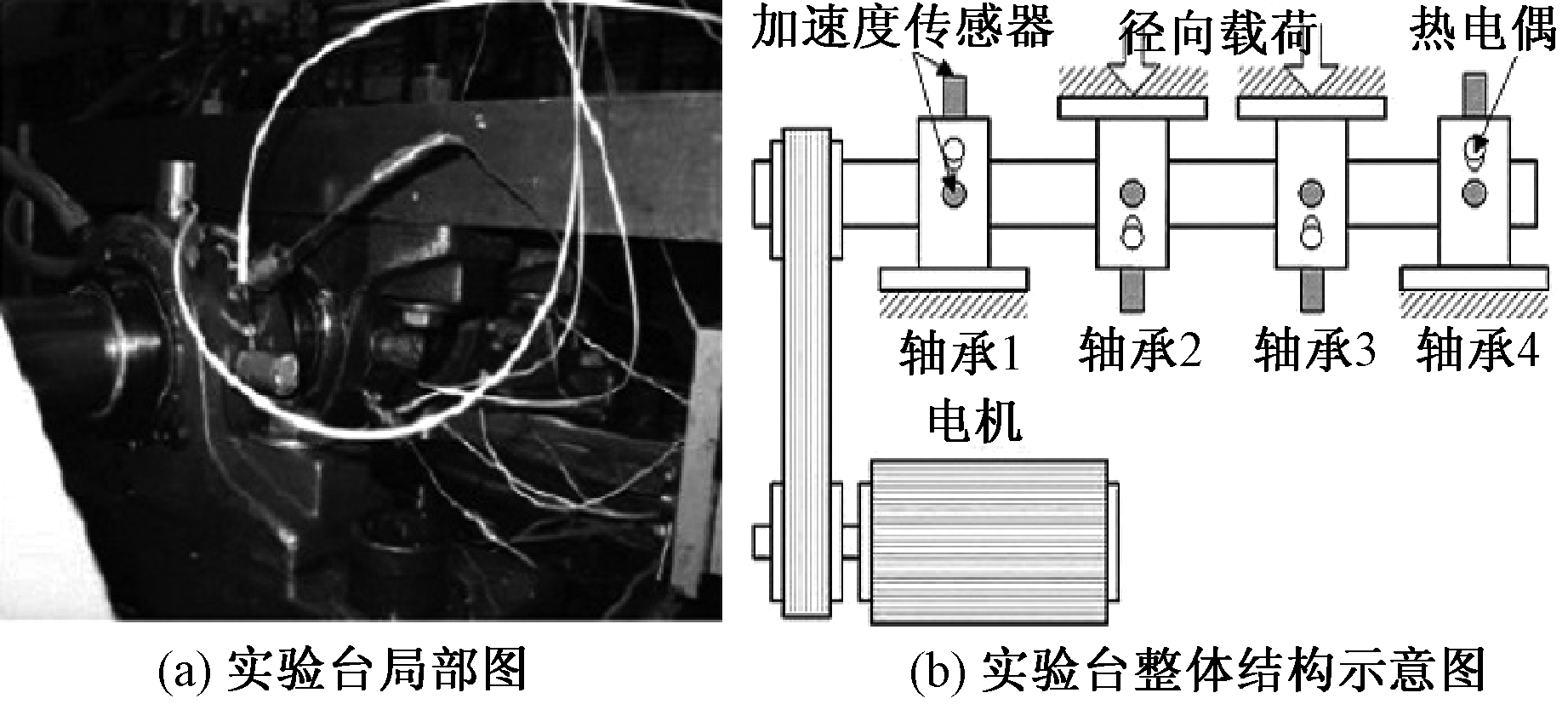
图3 实验装置说明图
Fig.3 Test Rig Illustration
为了更全面地获取信号中的特征信息,首先,利用全矢Hilbert方法对实验信号进行信息融合,得到各信号的Hilbert主振矢谱,并以其作为构造字典的训练样本.然后,利用自适应字典学习算法分别对处于内圈故障、外圈故障、滚动体故障及正常状态下的训练样本进行字典学习,得到滚动轴承在各状态下所对应的子字典.每类子字典的基函数个数为30,稀疏度为5,训练迭代次数为80.各类字典中的部分基函数波形如图4所示.
由图4可知,不同类型字典的基函数差别显著,而相同类型字典的基函数之间具有相似的统计规律.
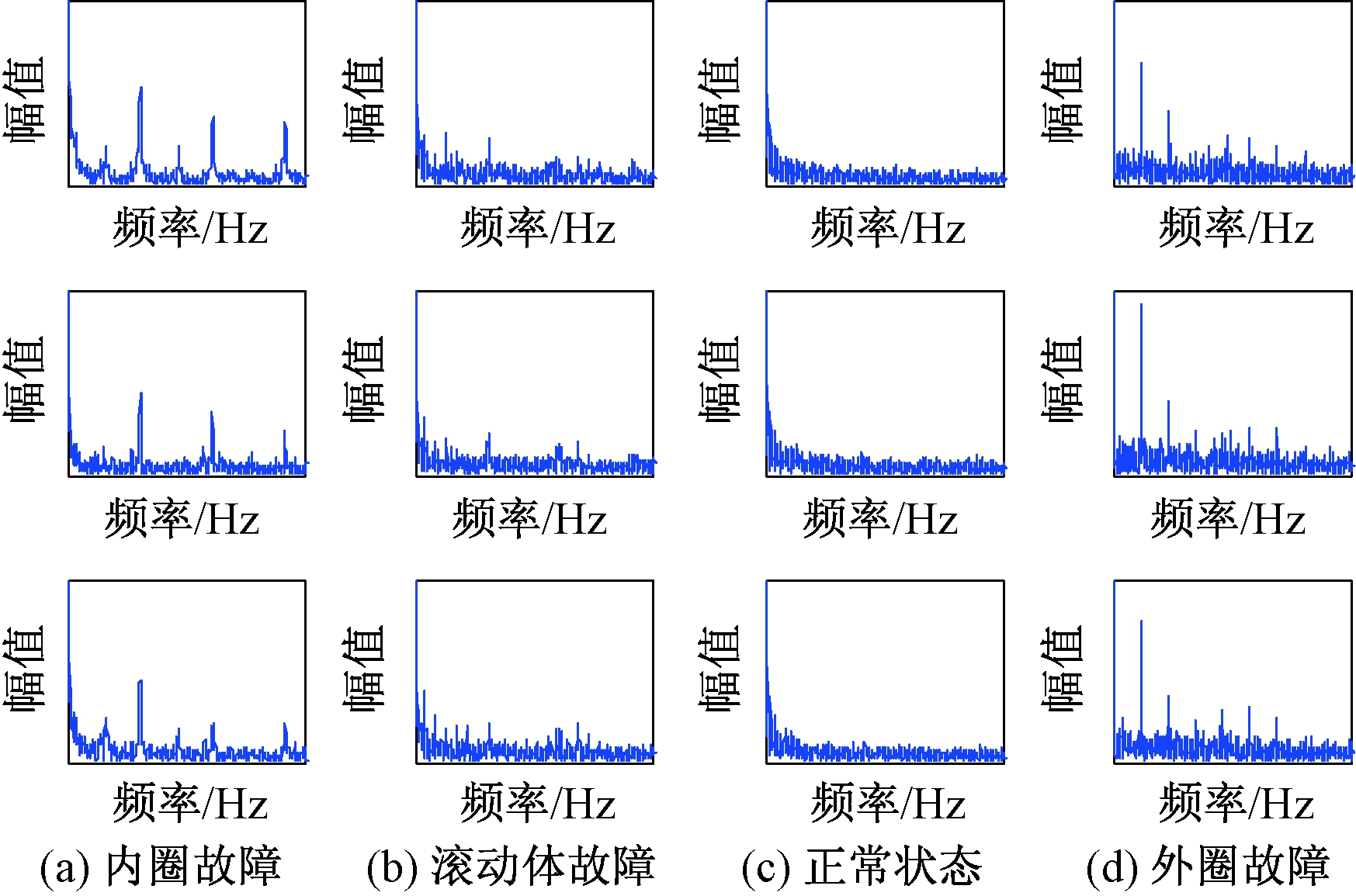
图4 各类字典中的部分基函数
Fig.4 Some basis functions of each class dictionary
为了验证本文所述方法的有效性,将各状态下的实验信号分割为长度为2 048点且不互相重叠的样本,共得到两个通道的样本各300组,然后将样本信号进行全矢信息融合,最后以融合后得到的Hilbert主振矢谱作为测试样本,利用已构造的各类子字典依次对其进行稀疏编码.实验表明:该方法在所有状态下的平均识别准确率为99.8%,所得到的部分相应重构误差结果(选取30组)如图5所示.图中:![]() ”表示采用不同状态类别的字典得到的重构结果,实线表示采用相同状态类别的字典得到的重构结果.
”表示采用不同状态类别的字典得到的重构结果,实线表示采用相同状态类别的字典得到的重构结果.
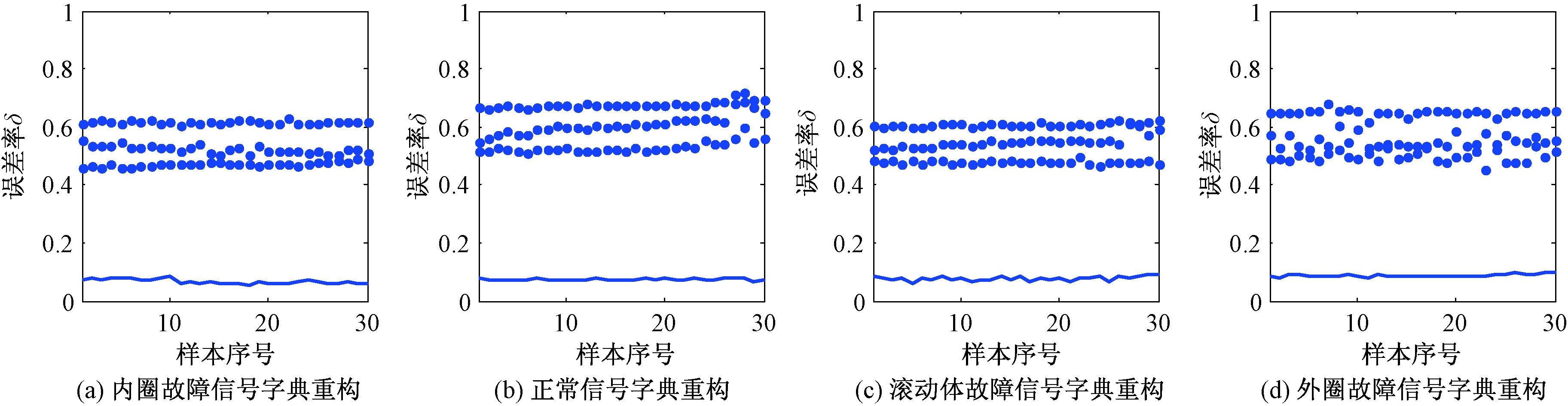
图5 全矢稀疏编码方法得到的分类结果
Fig.5 Classification result obtained by using the method of full vector sparse coding
由图5可知,各类测试样本在与其状态相同的字典下的稀疏重构误差率均远低于在其他字典下的稀疏重构误差率,因而可明显地识别出测试样本的状态类型,且具有很高的准确率.
文献[6,10]分别使用时域信号和单通道频谱作为训练样本构造字典,然后利用稀疏编码的特性对轴承进行了故障检测和分类.为了突出本文方法的优势,分别利用各状态下本实验轴承的时域信号和单通道频谱构造字典,其他分析步骤与本文方法相同,稀疏编码重构结果分别如图6和图7所示.
由图6可知,采用各类字典重构所得到的重构误差率的值很不稳定,区分度也较低.对于与各字典状态类别相同的测试样本,其重构误差率仍然较高,甚至多次出现高于其他类型测试样本的情况.因此,通过比较时域信号的重构误差率大小无法判断出测试样本的状态类型,即使用时域信号进行状态识别的效果不太理想.
由图7可知,相对于时域分析方法,基于单通道频谱的分析方法可有效识别实验轴承的状态类型,但是其识别准确率低于本文所提出的方法,而且测试样本在对应状态字典下的重构误差和在其他状态类别字典下的重构误差之间的区分度较低,误差率波动也较大,这说明基于单通道频谱的识别方法在稳定性方面也低于基于全矢谱的识别方法.

图6 以时域信号作为训练样本得到的分类结果
Fig.6 Classification result obtained by using time-domain signals as training data
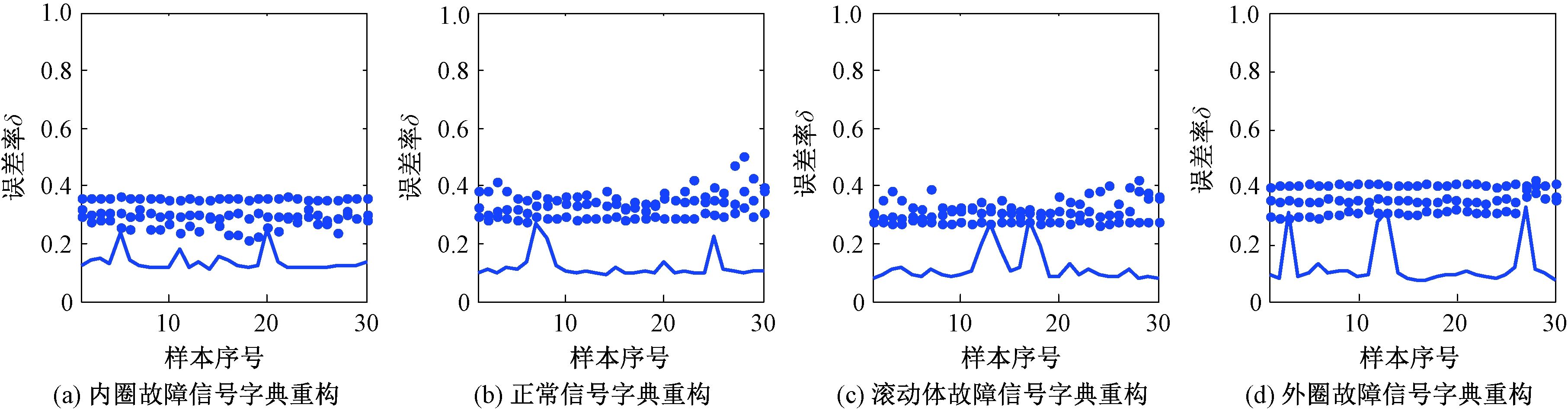
图7 以单通道频谱作为训练样本得到的分类结果
Fig.7 Classification result obtained by using single channel frequency spectrum as training data
综上所述,融合了双通道信息的全矢稀疏编码模式识别方法的综合性能优于时域分析方法和单通道频谱分析方法.
4 结论
(1)提出了一种结合全矢谱和稀疏编码的滚动轴承故障识别方法,将滚动轴承信号进行全矢信息融合后得到的主振矢谱作为训练样本进行字典学习,既解决了时域信号的特征时移问题,又解决了单通道信号的特征信息遗漏问题,提高了所构造字典的鲁棒性.实验结果表明,该方法能以较高的准确率和效率实现对滚动轴承信号的状态识别.
(2)与传统的稀疏编码模式识别方法相比,本文方法省去了人工提取特征的步骤,可减少前期工作量,在处理海量冗余数据方面具有明显的优势.
[1] 熊庆,张卫华.基于MF-DFA与PSO优化LSSVM的滚动轴承故障诊断方法[J]. 振动与冲击,2015, 34(11):188-193.
[2] WRIGHT J, YANG A Y, GANESH A, et al. Robust face recognition via sparse representation[J]. IEEE transactions on pattern analysis & machine intelli-gence, 2009, 31(2): 210-227.
[3] YANG M, ZHANG L, YANG J, et al. Metaface learning for sparse representation based face recognition[C]//IEEE International Conference on Image Processing.Hong Kong,China:IEEE, 2010: 1601-1604.
[4] DING X X, HE Q. Time-frequency manifold sparse reconstruction: A novel method for bearing fault feature extraction[J]. Mechanical systems & signal proces-sing, 2016, 80:392-413.
[5] LIU H N, LIU C L, HUANG Y X. Adaptive feature extraction using sparse coding for machinery fault diagnosis[J]. Mechanical systems & signal processing, 2011, 25(2): 558-574.
[6] 朱会杰,王新晴,芮挺,等. 基于频域信号的稀疏编码在机械故障诊断中的应用[J]. 振动与冲击, 2015, 34(21): 59-64.
[7] 李凌均, 陈超, 韩捷,等. 全矢支持向量回归频谱预测方法[J]. 郑州大学学报(工学版), 2016, 37(3):78-82.
[8] ZHANG H, CHEN X F, DU Z H, et al. Nonlocal sparse model with adaptive structural clustering for feature extraction of aero-engine bearings[J]. Journal of sound & vibration, 2016, 368:223-248.
[9] 苗中华,周广兴,刘海宁,等. 基于稀疏编码的振动信号特征提取算法与实验研究[J]. 振动与冲击, 2014, 33(15): 76-81.
[10] 张新鹏,胡茑庆,程哲,等. 信号稀疏分解理论在轴承故障检测中的应用[J]. 国防科技大学学报, 2016, 38(3): 141-147.