0 引言
在诸多建设工程中,建筑物基础经常被设置在靠近一定斜坡的地基上(简称临坡地基).在现行成果中,对临坡地基的破坏模式没有给出明确阐述,对临坡地基极限承载力的确定也没有给出具体计算方法.对于临坡地基,基础两侧土体埋深不同,因此并不能按传统的地基极限承载理论进行求解[1-2].Meyerhof[3]最早研究了临坡地基极限承载力问题,提出当地基距离斜坡较近时,其最终承载力将明显降低,同时其极限承载力将受到斜坡高度的显著影响,斜坡高度越大其承载力越低;Narita等[4]认为斜坡地基沿对数螺线面破坏,但没有进行深入研究;Saran等[5]针对临坡地基的破坏形态开展了相关研究,认为其基础底部的三角形弹性区并非呈左右对称分布;徐守国[6]、王晓谋[7]认为,条形基础荷载作用下的临坡地基,基础下两侧土体将按直线+螺旋线+直线的模式滑动;尉学勇等[8]推导出一个临坡地基极限承载力上限解公式,但结果缺少实验验证;杨峰等[9]、胡卫东等[10]等进行了临坡地基滑移破坏模式及极限承载力分析,但均没有考虑坡后土体的贡献.笔者基于双侧滑移破坏模型,采用解析及实验方法对临坡地基极限承载力进行研究,以期完善临坡地基极限承载力分析理论与方法.
1 极限平衡法计算
假设地基破坏时,基础下方为三角形弹性密实区,临坡一侧整体产生向外侧滑动,在坡后一侧土体则按虚拟滑移面方向产生滑动,滑动破坏模式如图1所示.
1.1 基本假定
①将浅埋条形基础的基底以上土重折算为超载进行计算;②基础底面按粗糙条件考虑,三角形弹性区的坡前、坡后侧底角分别为φ、φm;③土体采用理想弹塑性本构模型,服从摩尔-库仑屈服准则;④土体按直线+螺旋线+直线的模式滑动.
τ=c+σtan φ,
(1)
式中:φ为地基土内摩擦角;c为地基土黏聚力;σ为剪切滑动面上的法向应力;τ为剪切滑动面上的剪应力.
1.2 临坡地基计算模型
基于假想滑动面的分布形态,临坡地基土体由5个区块组成(如图1所示),滑动螺旋线AEK的中心点位置通过编程计算获取,该点处于直线EA的延长线上.坡后一侧土体存在DEFG假想滑动面,并用强度发挥系数m来对坡后土体强度进行折减,即在临坡地基达到极限承载状态时,坡后土体强度只是得到部分发挥,相应的坡后土体强度参数表示为:抗剪强度τm、黏聚力cm、内摩擦角φm.而三角形弹性区的坡后侧底角表示为φm,坡后螺旋滑动面EF的中心处于ED延长线方向或位于D点.
1.3 极限平衡法计算原理
临坡地基的极限承载力由三部分组成,其抗力效用3个承载力系数来表达,即Nr、Nq、Nc.则地基承载力为:
(2)
根据静力平衡条件,具体判断基底三角形弹性土楔ADE(如图2所示)的受力状态,建立平衡方程,通过编程计算得到m系数的取值.
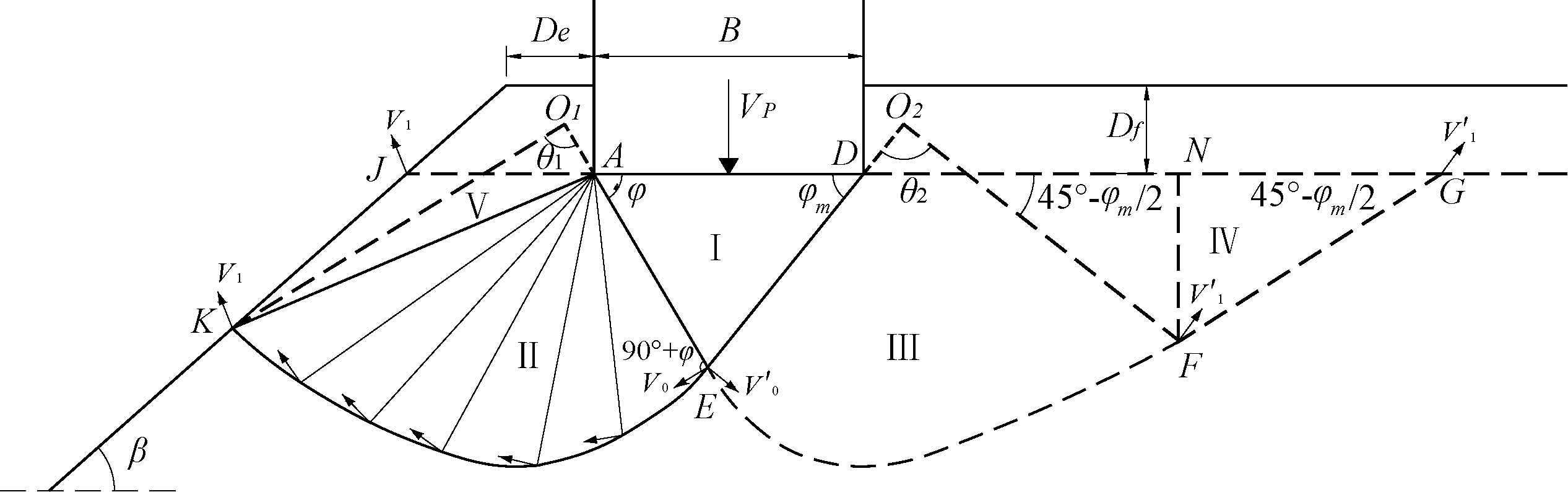
图1 临坡地基计算模型
Fig.1 Calculation model for ground foundation adjacent to slope
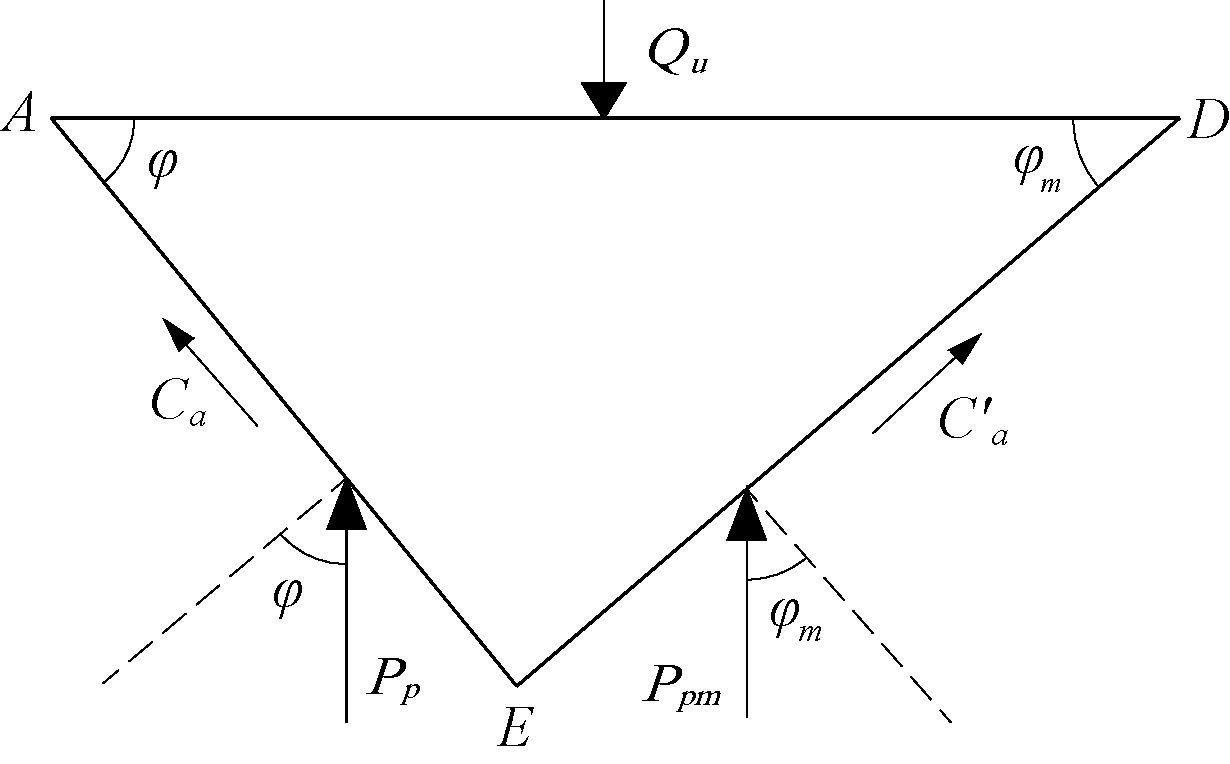
图2 基底弹性土楔ADE的受力示意图
Fig.2 Forces on elastic wedge ADE
坡前及坡后土体被动土压力均由三部分构成,则三个承载力系数可表示为:
(3)
(4)
(5)
式中:Ppr、Ppq、Ppc可根据土体AEKJ的平衡条件求得,如图1、图3所示;Ppmr、Ppmq、Ppmc可根据土体DEFN的平衡条件求得,如图1、图4所示.
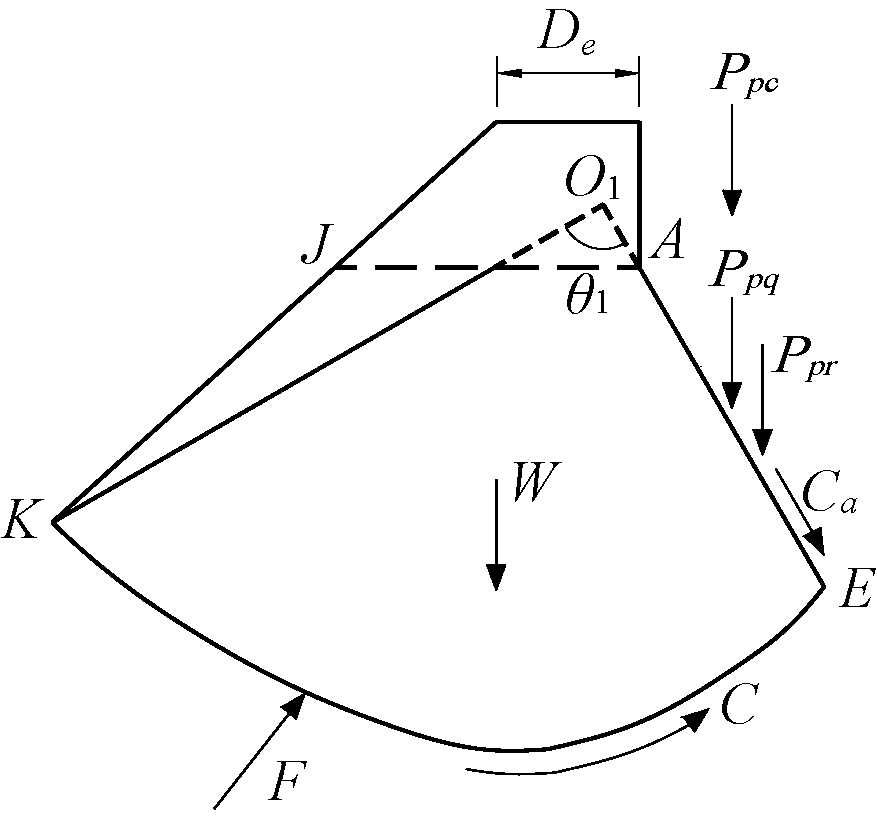
图3 AEKJ上的力系
Fig.3 Forces on soil mass AEKJ
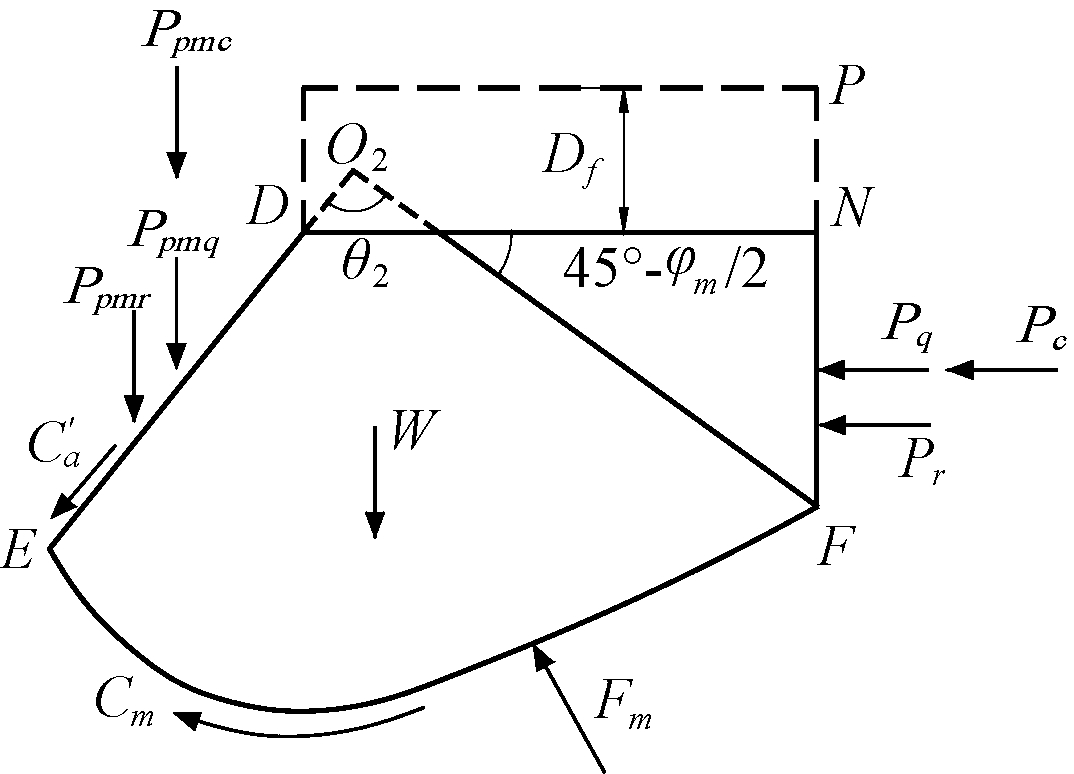
图4 DEFN上的力系
Fig.4 Forces on soil mass DEFN
Ppr、Ppq、Ppc及Ppmr、Ppmq、Ppmc为地基土物理力学参数、几何尺寸及发挥系数m的函数.根据三角形土楔ADE的力矩平衡条件可通过试算法计算出c=q=0、c=γ=0、q=γ=0时的发挥系数m,进而求出Ppr、Ppq、Ppc及Ppmr、Ppmq、Ppmc值.
1.4 典型m值计算结果
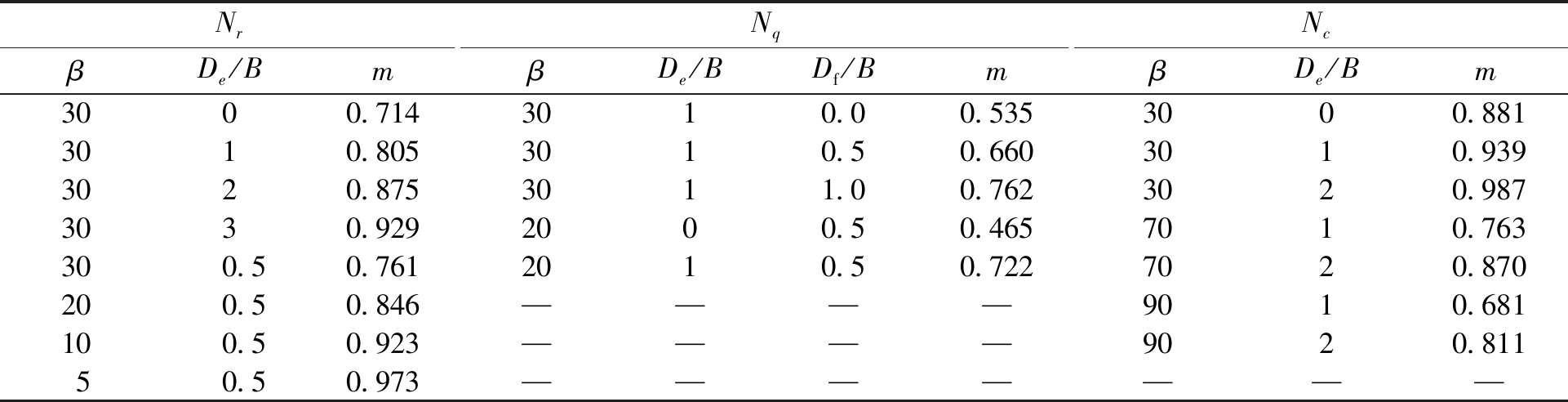
在表1中列出了典型m值计算结果,可以看出:边坡坡度一定时,m随相对坡顶距增大而增大;相对坡顶距一定时,m随边坡坡度的增大而减小;边坡坡度及相对坡顶距均一定时,m随相对埋深的增大而增大.
2 极限分析法求解
基于假想的临坡地基双侧非对称破坏模型(图1),通过极限分析上限定理,求得满足运动许可速度场的临坡地基极限承载力上限解[11].在此基础上,进一步对比极限平衡法计算结果,寻求临坡地基极限承载力的真实解答,并有效验证
表1 典型m值计算结果(φ=40°)
Tab.1 Computed results for representative values of m
NrNqNcβDe/BmβDe/BDf/BmβDe/Bm3000.7143010.00.5353000.8813010.8053010.50.6603010.9393020.8753011.00.7623020.9873030.9292000.50.4657010.763300.50.7612010.50.7227020.870200.50.846————9010.681100.50.923————9020.81150.50.973———————
不同计算方法的合理性与可靠性.
2.1 基本假定
①采用理想弹塑性本构模型,服从摩尔-库仑屈服准则;②在极限分析中,运用相关联流动法则,基于塑性理论计算土体应力应变特征;③运用虚功原理,忽略土体破坏时的瞬时变形.
极限分析法取用与极限平衡法相同的假想滑动面,如图1所示.
2.2 地基极限承载力公式
应用上限定理,建立虚功方程:
∑D=∑W+∑P,
(6)
式中:∑D为地基土内部能量耗损率;∑W为地基土自重所作功;∑P为外荷载所作功.
基于图1所示的假想破坏机构,求解∑D、∑P及∑W,并代入虚功方程,令![]() 可得到地基极限承载力Qu表达式:
可得到地基极限承载力Qu表达式:
Qu=![]()
3tan φcos(θ1+φ)]-4sin φ}-
c·r0·cot φsec φ(e2θ1tan φ-1)+c·r0·sin φ+
(7)
将![]() 代入式(7),并令
代入式(7),并令![]() 进一步整理可得承载力系数表达式:
进一步整理可得承载力系数表达式:
Nr=![]()
![]() {e3θ1tan φ[sin(θ1+φ)+
{e3θ1tan φ[sin(θ1+φ)+
3tan φcos(θ1+φ)]-4sin φ}-
![]()
![]()
![]() }-
}-
(8)
Nq=![]()
cos(θ1+φ)sec φ·eθ1 tan φ.
(9)
Nc=![]() ·(e2θ1 tan φ-1)+
·(e2θ1 tan φ-1)+
![]()
(10)
2.3 计算结果比较
两种方法的计算结果如表2所示.从表2可以看出,承载力系数Nr、Nq、Nc随影响因素De/B、Df/B、φ、β的变化趋势基本一致.
表2 极限分析法与极限平衡法结果对比
Tab.2 Comparison of results obtained by limit equilibrium and limit analysis approaches

De/Bφ=40°,β=30°, Df/B=1极限分析法极限平衡法NrNqNcNrNqNc0.095.95115.47073.57193.94713.50472.2211.0126.34231.18382.443124.50228.78380.6432.0150.94552.05282.974148.78150.04981.214
3 离心模型试验
制作部分典型工况的临坡地基模型,利用土工离心机开展相关离心模型试验研究.有效揭示临坡地基在极限承载状态下的滑移破坏特征,并定量分析诸多影响因素(如基础尺寸、地基模型几何尺寸、荷载条件等)对于临坡地基极限承载力的具体影响.
3.1 试验设备及方法
3.1.1 土工离心机
土工离心机的组成如图5所示,主要由挂斗、转臂、支座、连轴器、减速器、传动轴、调速电动机及其控制器等组成,其主要参数如表3所示.

图5 50gt土工离心机
Fig.5 50gt geotechnique centrifuge
表3 TH-50gt土工离心机参数
Tab.3 Parameters of 50gt geotechnique centrifuge

有效半径/m最大加速度最大荷载/(g·t)电机功率/kW2250 g5055
3.1.2 模型箱
试验中固壁式模型箱内部尺寸长×宽×高为500 mm×200 mm×350 mm,在模型箱内壁粘贴减震塑料板,以减少反射波的影响.在模型箱一侧装有透明的有机玻璃,厚40 mm,用于观察试验过程中模型的变形破坏过程.
3.1.3 加载系统
离心场坡表加载系统通过加载板对基础的顶面施加荷载,该系统主要由加速器、涡轮蜗杆以及直流永磁电机组成,整个加载以恒定位移速率进行.
3.1.4 非接触位移测量系统
位移测量系统及高质量离心场图像采集系统能够对试验过程中土体的变形进行测量和记录,即通过固定的摄像头对土体侧面进行拍摄,再通过远程计算机系统进行记录,并加以分析和处理,从而得到试验中土体位移的完整数据.
3.2 试验方案与试验模型
3.2.1 试验方案
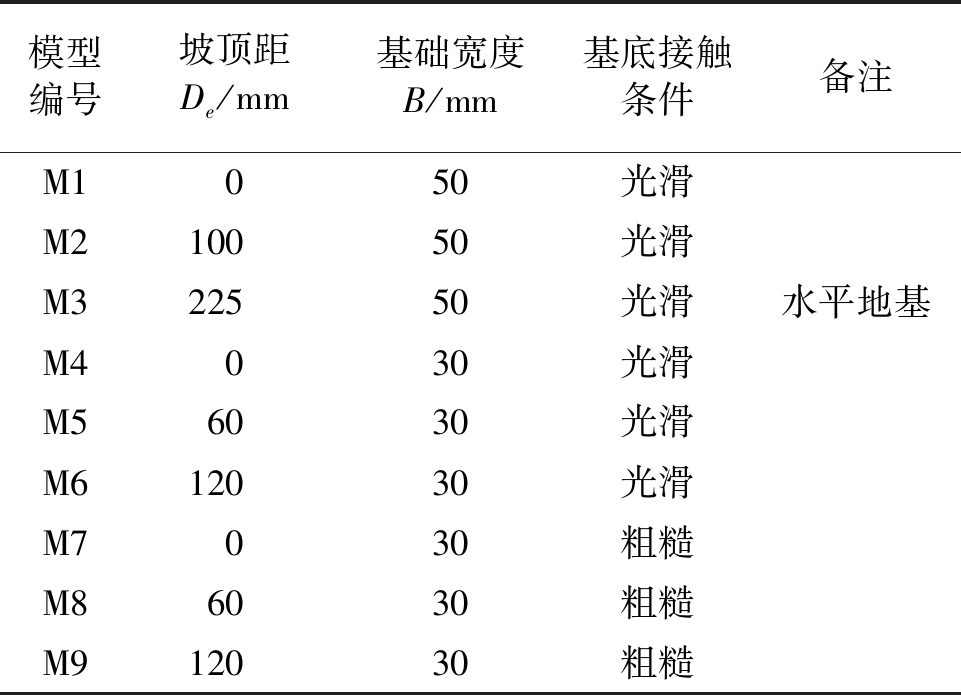
受模型箱尺寸的限制,将需研究的斜坡地基按照一定的比例缩小,制作成试验模型.根据研究目标,设计3组试验模型,每组设计3种工况,具体如表4所示.
表4 模型制作方案一览表
Tab.4 Make scheme of test model
模型编号坡顶距De/mm基础宽度B/mm基底接触条件备注M1050光滑M210050光滑M322550光滑水平地基M4030光滑M56030光滑M612030光滑M7030粗糙M86030粗糙M912030粗糙
若基底接触条件为光滑,则在基础上设置专门的滑块来实现基础与地基之间的光滑接触;若基底接触条件为粗糙,则去掉滑块,同时在基础底面贴上砂纸来实现粗糙接触.
3.2.2 试验模型
采用黏性土制作离心试验模型.对制备好的土样进行分层击实,并严格控制土样的干密度指标.再削去多余土样,制作成临坡地基土体模型,土样高度为20 cm.为降低基座对试验结果的影响,模型土体下半部分的水平土层应保留10 cm的厚度.此外,在模型箱的两侧均涂抹硅油,以降低模型土体与模型箱侧壁之间的摩擦力,并在模型箱外侧粘贴聚四氟乙烯膜.同时,为了保证在试验中土坡可以向临空面方向自由变形,模型的坡脚与模型箱侧壁之间保留一定距离.
3.3 试验结果分析
试验表明,试验模型的实际破坏形态与前述假定破裂面相似.
3.3.1 不同条件下的临坡地基极限承载力
(1)不同地基类型.从图6可见,在地基土参数相同条件下,水平地基的极限承载力明显高于斜坡地基.临坡地基与水平地基的q-s曲线形态存在差异,在开始阶段,临坡地基的承载力增长较快,后期逐步趋于平缓;而水平地基的承载力增长较为平缓,更为均匀.
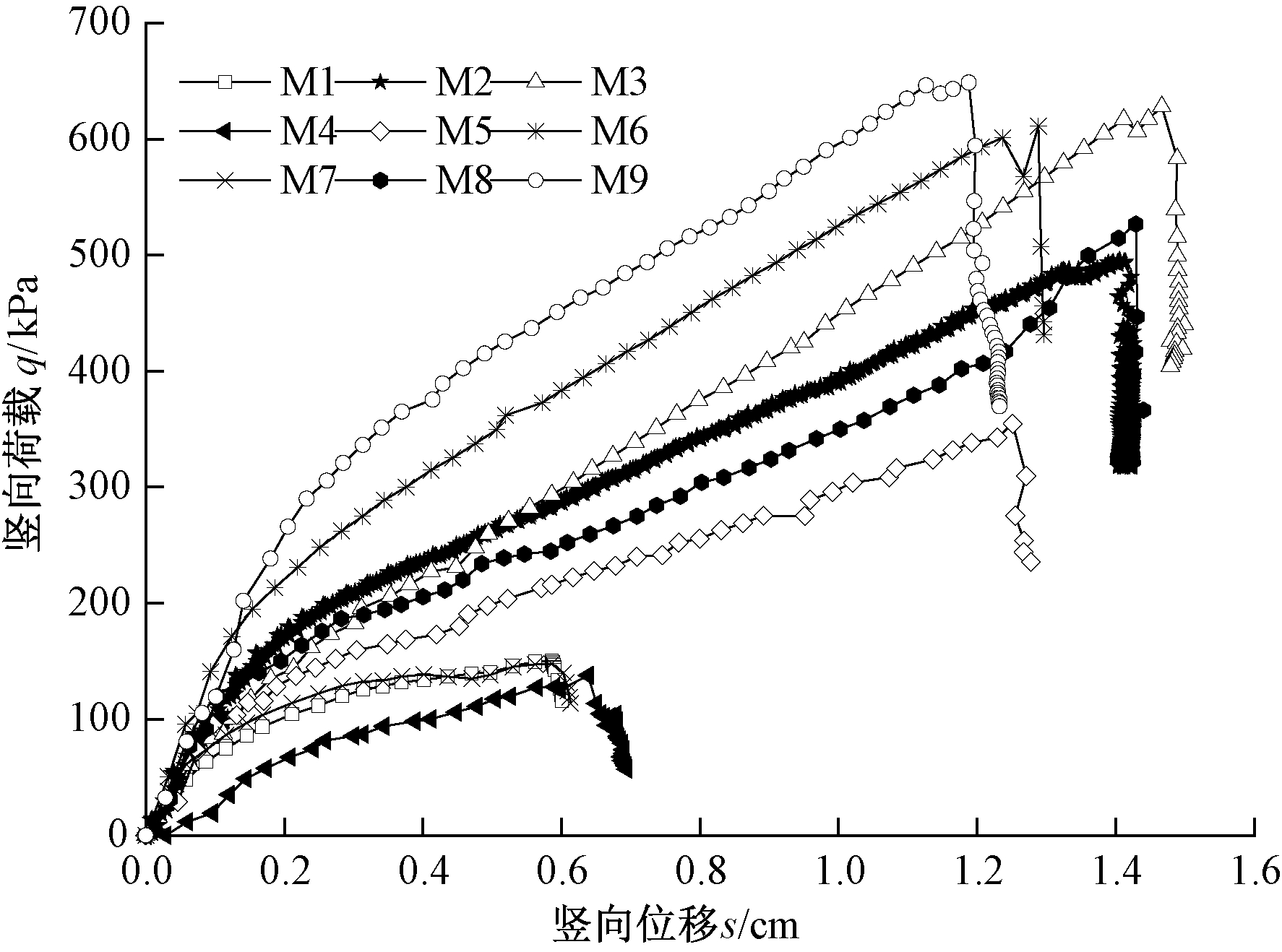
图6 地基类型对极限承载力的影响
Fig.6 Influence of ground foundation type on bearing capacity
(2)不同基础宽度.试验表明,M5与M2模型相比,同样坡顶距为两倍基础宽,但破坏形态有所差异:M5模型地基变形更快,破坏事件更短;M5模型的地基土变形扩展范围更小,坡顶拉裂缝分布更为集中;M5模型斜坡上土体溢出位置更靠近坡顶.从图6可见,条形基础宽度对临坡地基的极限承载力有一定的影响[12].其他条件均相同时,基础宽度越大,临坡地基极限承载力越高,如M1模型的极限承载力高于M4模型,M2模型的极限承载力高于M5模型,q-s曲线形态基本一致.
(3)不同坡顶距.从图6可见,坡顶距对于临坡地基极限承载力具有显著影响,坡顶距越大,地基极限承载力越高;坡顶距越大,地基破坏时,基础达到的位移越大,而坡顶距较小时,滑移土体范围较小,地基很快形成连贯滑移面;另外,坡顶距较大时,地基存在明显渐进破坏过程;再者,坡顶距越大,在加载稳定阶段,q-s曲线斜率越大,即随着基础的下沉,地基土强度发挥更加充分[13].
(4)不同基底接触条件.试验表明,基底接触条件对于临坡地基极限承载力具有显著影响.基底粗糙相对于基底光滑条件,承载力的提高主要体现在加载初期.在加载初期,基底粗糙时,基础底面与地基顶面的摩阻作用约束了土体的侧向位移,在基础下方形成弹性核.相对于光滑基础,粗糙基础下的土体压缩时间持续更长,地基深处土体发生侧向滑移时间相对延后,在图6中表现为,加载初期(如s<0.4 cm),基底粗糙条件下的q-s曲线斜率更大.在加载后期,两种基底接触条件下的地基承载力增长速度相差不大,即q-s曲线斜率基本相等.
3.3.2 试验结果与理论计算结果的比较
在本次离心模型试验方案中,基底接触条件为粗糙的有M7、M8、M9号模型,在此对上述模型计算结果进行对比.
由式(2)可知,临坡地基的极限承载力计算公式为:
(11)
式中:Nγ、Nq、Nc为承载力系数,在极限平衡方法中分别按式(3)、式(4)、式(5)计算,在极限分析法中分别按式(8)、式(9)、式(10)计算;γ为地基材料的重度,根据前述试验用土的干密度、含水量,可换算得到地基土的自然重度为16.45 kN/m3;B为条形基础宽度,根据离心模型试验的相似比,可确定原型中的基础宽为1.2 m;c为地基材料黏聚力,与离心模型试验中相同,取为22 kPa;Df为基础埋深,无埋深,取为0.
将上述参数代入式(11),可得
qu=9.87Nr+22Nc.
(12)
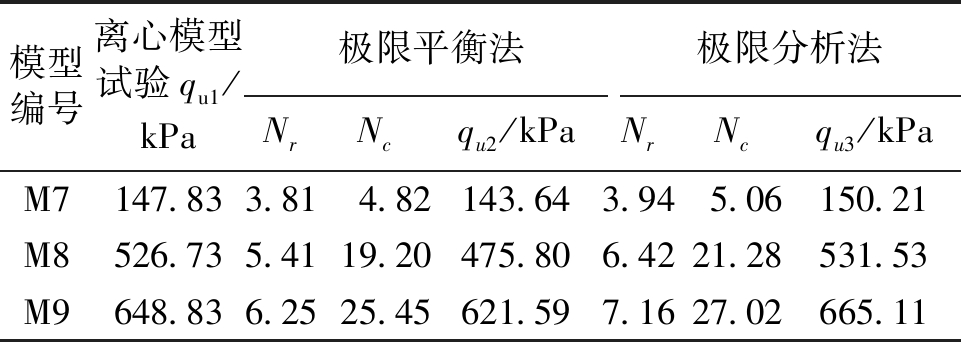
根据地基土的物理力学参数及基础相对位置等几何尺寸参数,按前述极限平衡法和极限分析法进行计算,可得到承载力系数,代入式(12)可求得相应结果,如表5所示.
结果表明,理论计算结果与离心模型试验结果较为吻合,总体误差在10%以内.另外,试验值介于极限平衡法和极限分析法计算结果之间,极限平衡法相对较低,而极限分析法相对较高,主要原因在于极限平衡及极限分析法计算中,计算模型及假想滑动面的选择与实际存在一定的误差.
表5 试验结果与理论计算结果比较一览表
Tab.5 Comparison of results by test and theoretical calculation
模型编号离心模型试验qu1/kPa极限平衡法 极限分析法NrNcqu2/kPaNrNcqu3/kPaM7147.833.814.82143.643.945.06150.21M8526.735.4119.20475.806.4221.28531.53M9648.836.2525.45621.597.1627.02665.11
4 结论
笔者引入坡后土体强度发挥系数的概念,考虑坡后土体强度的折减,从而建立双侧非对称破坏模式的临坡地基极限承载力计算模型.通过编程计算,获得极限平衡条件下的坡后土体强度折减值,以m值表征.计算结果表明:边坡坡度一定时,m随相对坡顶距增大而增大;相对坡顶距一定时,m随边坡坡度的增大而减小;边坡坡度及相对坡顶距均一定时,m随相对埋深的增大而增大.进而,基于极限平衡法和叠加原理,可求得承载力系数Nr、Nq、Nc的表达式.
基于假定临坡地基极限承载力计算模型,构建运动许可速度场,进行极限分析计算,得到地基极限承载力上限解.3个承载力系数的计算结果显示,极限平衡法计算结果略小于极限分析法计算结果,但3个承载力系数随影响因素De/B、Df/B、φ、β的变化规律基本一致.
利用离心模型试验定性分析了临坡地基在极限承载状态下的变形破坏特征,定量分析了诸多影响因素对于其极限承载力的具体影响.
试验结果表明:①临坡地基与水平地基的q-s曲线形态存在差异,在开始阶段,斜坡地基的承载力增长较快,后期逐步趋于平缓;而水平地基的承载力增长较为平缓,更为均匀.②其他条件均相同时,基础宽度越大,临坡地基极限承载力越高.③坡顶距较小时,滑移土体范围较小,地基很快形成连贯滑移面;而坡顶距较大时,地基存在明显渐进破坏过程.④基底接触条件对于临坡地基极限承载力具有显著影响.在加载初期,粗糙基础下方局部土体压缩时间更加持久,q-s曲线斜率更大;在加载后期,两种基底接触条件下的地基承载力增长速度相差不大.
离心模型试验结果与理论计算结果较为吻合,总体误差在10%以内,文中所述理论方法可为实际工程计算提供借鉴.
[1] 徐洋,谢康和,刘干斌,等. 复合双层地基的极限承载力计算[J]. 土木工程学报,2004,37(4):82- 86.
[2] 马强,朱健,邢文文,等. 具有硬壳层的涵洞地基极限承载力分析[J]. 郑州大学学报(工学版),2016,37(1):70-74.
[3] MEYERHOF G G. The ultimate bearing capacity of foundations on slopes-lafore portante des foundation sur talus[C]∥The Proceedings of the Fourth International Conference on Soil Mechanics and Foundation engineering. London:Routledg, 1957:384-386.
[4] NARITA K, YAMOGUCHI H. Bearing capacity analysis of foundations on slopes by use of log-spiral sliding surfaces[J]. Soils and foundations,1990, 30(3): 144-152.
[5] SARAN S, SUD V K, HANDA S C. Bearing capacity of footings adjacent to slopes[J]. Journal of geote-chnical engineering,1989, 115(4): 553-573.
[6] 徐守国. 斜坡上地基承载力的研究[D]. 西安: 西安公路学院,1992.
[7] 王晓谋,徐守国. 斜坡上的地基承载力的有限元分析[J]. 西安公路学院学报,1993,13(3):13-17.
[8] 尉学勇,王晓谋,怀超. 斜坡地基极限承载力上限解计算与分析[J]. 岩土工程学报,2010,32(3):381-387.
[9] 杨峰,阳军生,张学民,等. 斜坡地基单侧滑移破坏模式及承载力上限解[J]. 工程力学,2010,27(6):162-168.
[10] 胡卫东,曹文贵. 基于Meyerhof理论的临坡地基极限承载力简化分析方法[J].湖南大学学报(自然科学版),2015,42(1):81-89.
[11] CHEN W F. Limit analysis and soil plasticity[M].New York:Elsevier,1975.
[12] 杨光华,王恩麒.基础宽度对地基承载力影响的数值分析[J].岩土力学,2013,34(增刊2):383-392.
[13] 余新才,李剑,尚义敏,等. 斜坡地基承载力及其影响因素的数值模拟研究[J]. 科学技术与工程,2012,12(35):9753-9759.