0 引言
近些年来,全断面隧道掘进机(tunnel boring machine,TBM)由于其开挖效率高、安全性好、对周围环境扰动小等优点已经被广泛应用于地下洞室的开挖中。TBM开挖过程中会遇到各种复杂的地质条件,如高地应力、节理发育、软弱复合地层、岩溶等。这些不良地质条件给TBM施工带来了很大困难,会造成开挖效率低、卡机、停工,甚至危及周围环境的人员安全及生命财产。
目前,许多专家学者针对节理发育这一不良地质因素对TBM滚刀破岩的影响进行了大量的实验和数值模拟研究。Gong等[1]和Bejari等[2]采用离散元法对节理发育程度和特征对TBM滚刀破岩过程和破岩效率的影响进行了研究;邹飞等[3]、谭青等[4]、张银霞等[5]针对不同节理特征条件对隧道掘进破岩特征的影响进行试验和数值模拟研究。在研究节理特征对TBM破岩影响的过程中,连续节理的间距和倾角是热点,极少针对断续节理的几何特征对TBM破岩的影响进行研究。
近两年,Li等[6]采用岩体相似材料,通过室内实验研究了单根断续节理模型在TBM刀头侵入情况下,不同的节理位置、倾角以及不同的节理填充情况下,模型的破坏模式和破坏效率。杨圣奇等[7]采用颗粒流模拟单滚刀作用下单根断续节理岩体的破岩过程,得到随着裂隙倾角的增大在裂隙尖端更容易萌生翼型裂纹,裂隙岩体比完整岩体更容易发生破坏的结果。从他们的研究成果发现,断续节理对TBM滚刀破岩过程的影响区别于连续节理。
笔者采用一种新的无网格数值模拟方法GPD[8]研究TBM滚刀破岩机理。在以前的工作中,GPD法已成功应用于模拟连续节理对TBM滚刀破岩效果的影响[9-10]。笔者运用GPD法研究断续节理的倾角对TBM滚刀破岩模式和破岩效率的影响。
1 GPD算法的基本理论
1.1 本构模型
通常情况下,岩石材料表现出脆性特性,为模拟滚刀作用下压碎区的形成和裂纹的起裂、扩展问题,笔者采用弹脆性本构关系,如图1所示。
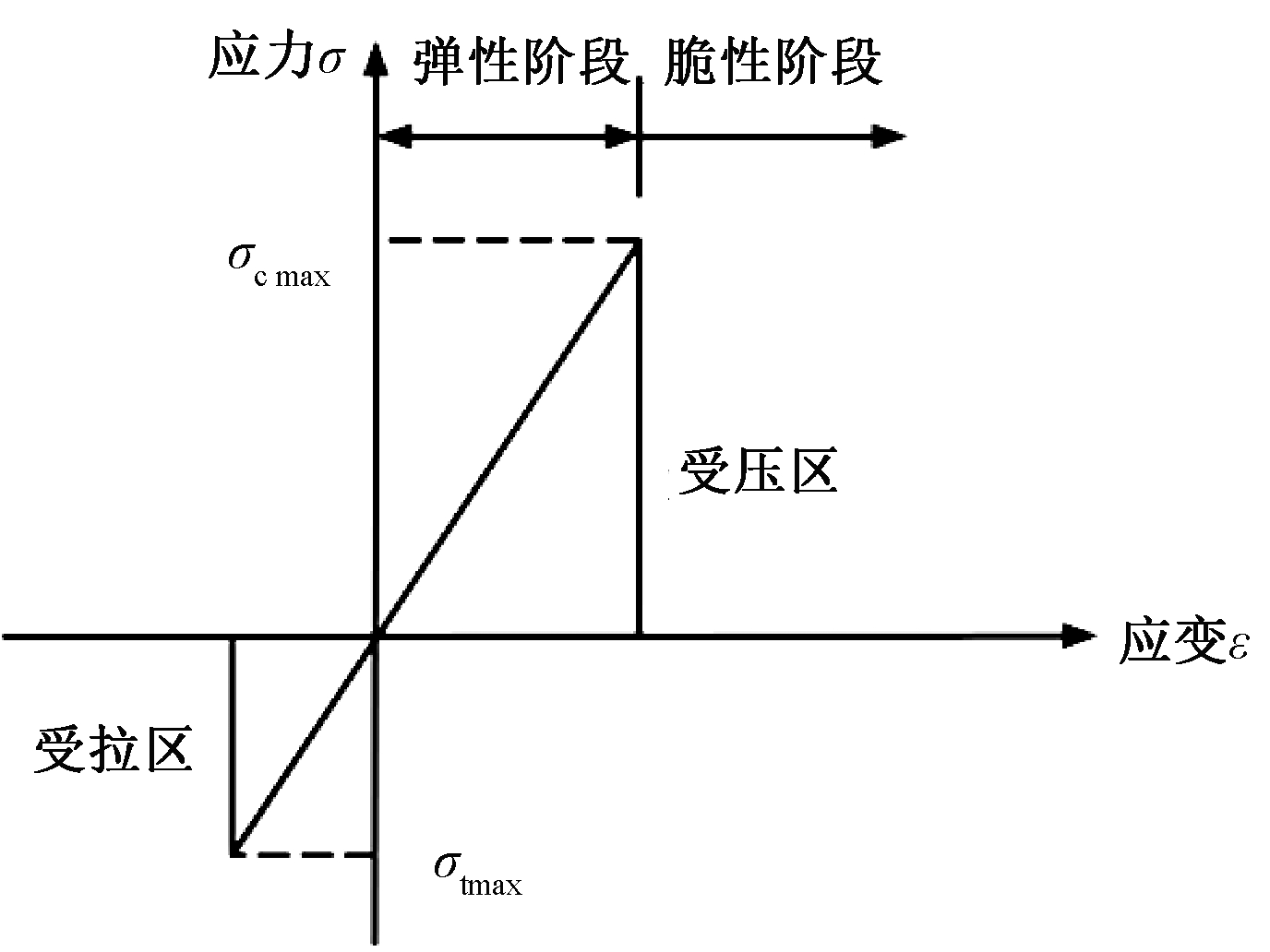
图1 线性弹脆性法则
Figue 1 Linear elastic brittle law
笔者采用Hoek-Brown强度对损伤的开始和扩展进行判断。Hoek-Brown强度准则可以表述为[11]:
(1)
在本文模拟中采用的岩体为多矿物结晶的粗粒花岗岩,其岩体质量好、轻微风化,力学参数如表1所示。根据岩体质量和强度参数m和s之间的关系表[12],本文中强度参数m、s分别取2.5、0.004。
表1 岩体的力学参数
Table 1 Mechanical parameters of rock

力学参数数值密度/(kg·m-3)2780内摩擦角/(°)30°黏聚力/MPa25弹性模量/GPa23泊松比0.19单轴抗压强度/MPa108
1.2 GPD算法的程序化
图2给出了GPD算法实现程序化的流程图。
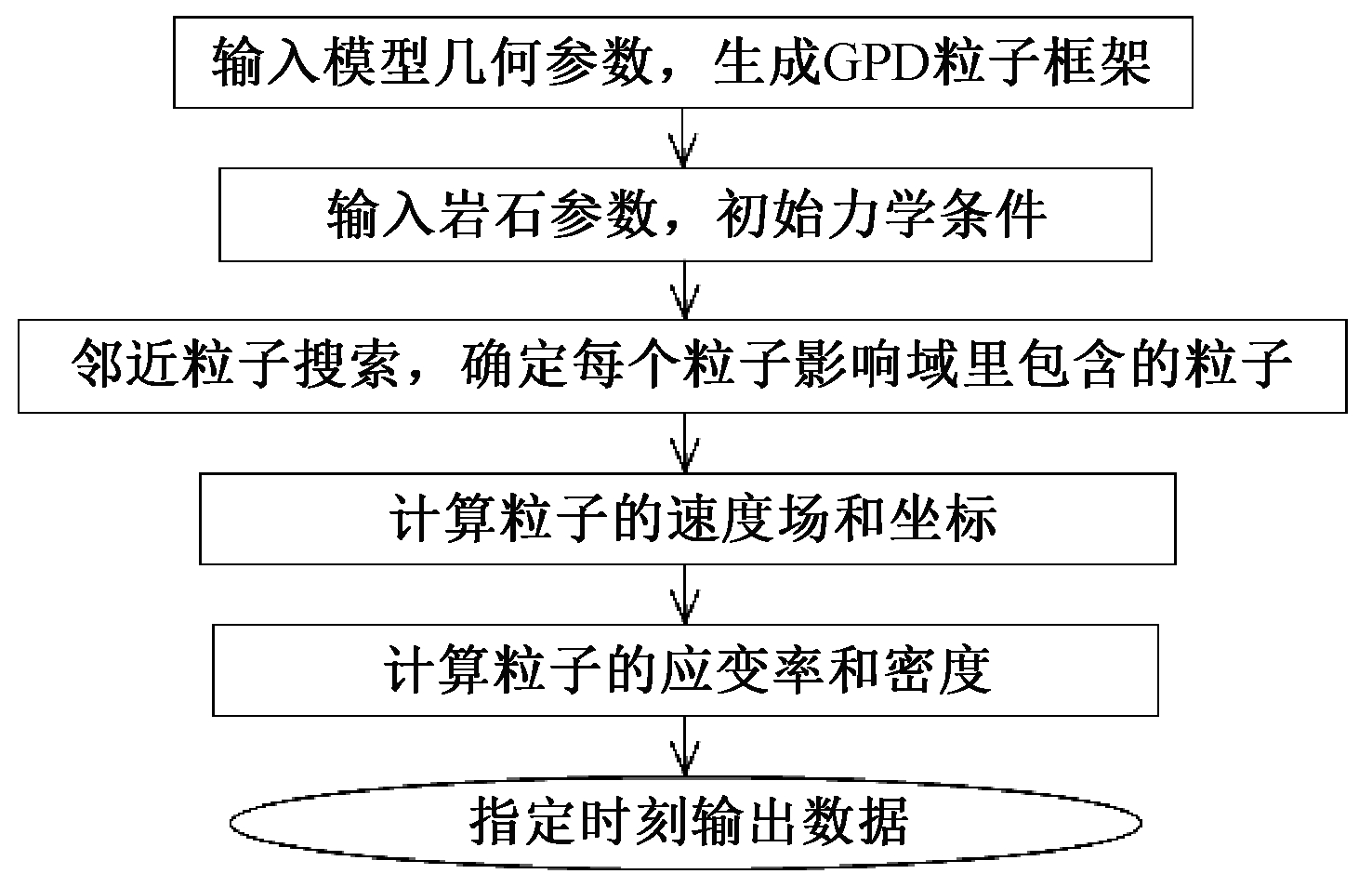
图2 GPD程序流程
Figue 2 The flow chart of GPD program
2 建立模型
如图3所示,建立单根断续节理单滚刀破岩模型,模型尺寸为0.1 m×0.1 m,断续节理在程序中通过挖掉该处的粒子来实现。断续节理的中心点位于模型的对称轴上,且距离加载面的距离为40 mm,断续节理的倾角用β表示。节理长度为40 mm,节理倾角β取0°、15°、30°、45°、60°、75°和90°。模型中忽略滚刀的切向滚动力和侧向力,采用位移加载方式模拟滚刀的法向力,法向力与上边界接触宽度为15 mm。位移加载速度为0.01 m/s,属于拟静力加载方式。上边界为自由边界,左、右、下边界为固定位移边界。
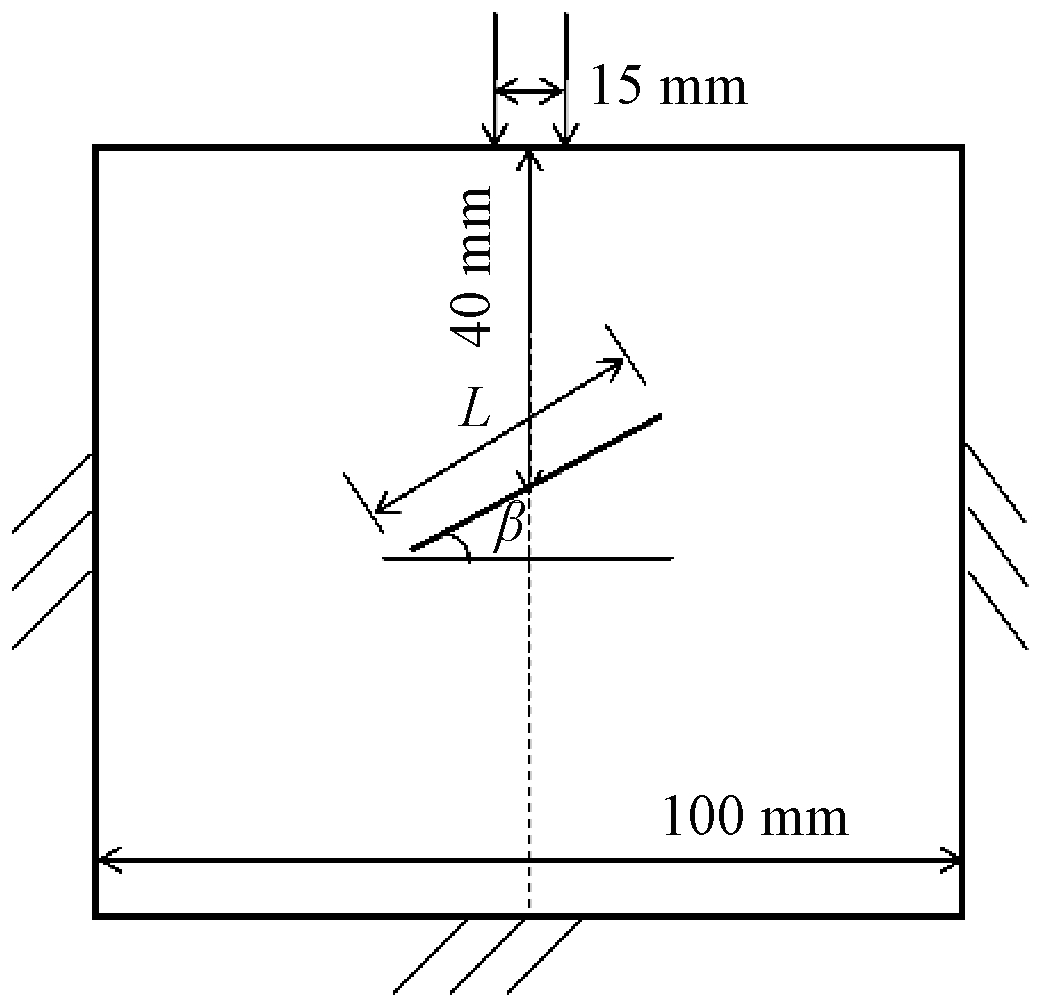
图3 单滚刀侵入断续节理岩体的模型
Figue 3 Numerical simulation model of the intrusion into intermittent jointed rock by one cutter
3 断续节理倾角对TBM滚刀破岩的影响
3.1 断续节理岩体的TBM滚刀破岩过程
图4(A)~(G)分别给出了不同节理倾角下,滚刀贯入度P为0.12 mm、0.42 mm、0.72 mm、1.02 mm所对应的破岩状态。图中粒子类型3代表破坏粒子(红色),粒子类型2代表非破坏粒子(蓝色),白色线条代表断续节理的位置。
由图4(A)~(G)可以看出,单滚刀侵入不同倾角的断续节理岩体时,破岩过程大致相同,可以分为3个阶段:①压碎区形成阶段,如图4(A)~(G)中的图(a);②裂纹区形成阶段,如图4(A)~(G)中的图(b);③断续节理处裂纹的起裂扩展阶段,如图4(A)~(G)中的图(c)和(d)。
如图4(A)~(G)中的图(a)所示,滚刀向岩体加载时,在滚刀的下方形成扇形压碎区。如图4(A)~(G)中的图(b)所示,在滚刀下方压碎区的两边可以看到不规则的锥形裂纹,这些裂纹形状像赫兹波,被称为赫兹裂纹[12]。在压碎区的下方存在长度大于2 mm,并且扩展方向垂直向下的裂纹,称为中央裂纹[13]。同时,在断续节理位置处有破坏点出现。如图4(A)~(G)中的图(c)和(d)所示,中央裂纹、赫兹裂纹及起裂于断续节理处的微裂纹均不断扩展。
应力的扩展是导致裂纹起裂和扩展的原因,图5给出了断续节理倾角β=0°、滚刀贯入度P=1.02 mm时,滚刀作用下最大主应力分布图,可以得到:①在压碎区的下方存在高应力区,且随着与加载点的距离的增大,应力逐渐减小;②中央裂纹、赫兹裂纹及断续节理尖端为拉应力;③断续节理的存在对应力的传播有一定的阻挡作用,将应力的扩展限定在一定范围内,有利于滚刀下方岩体的破碎。
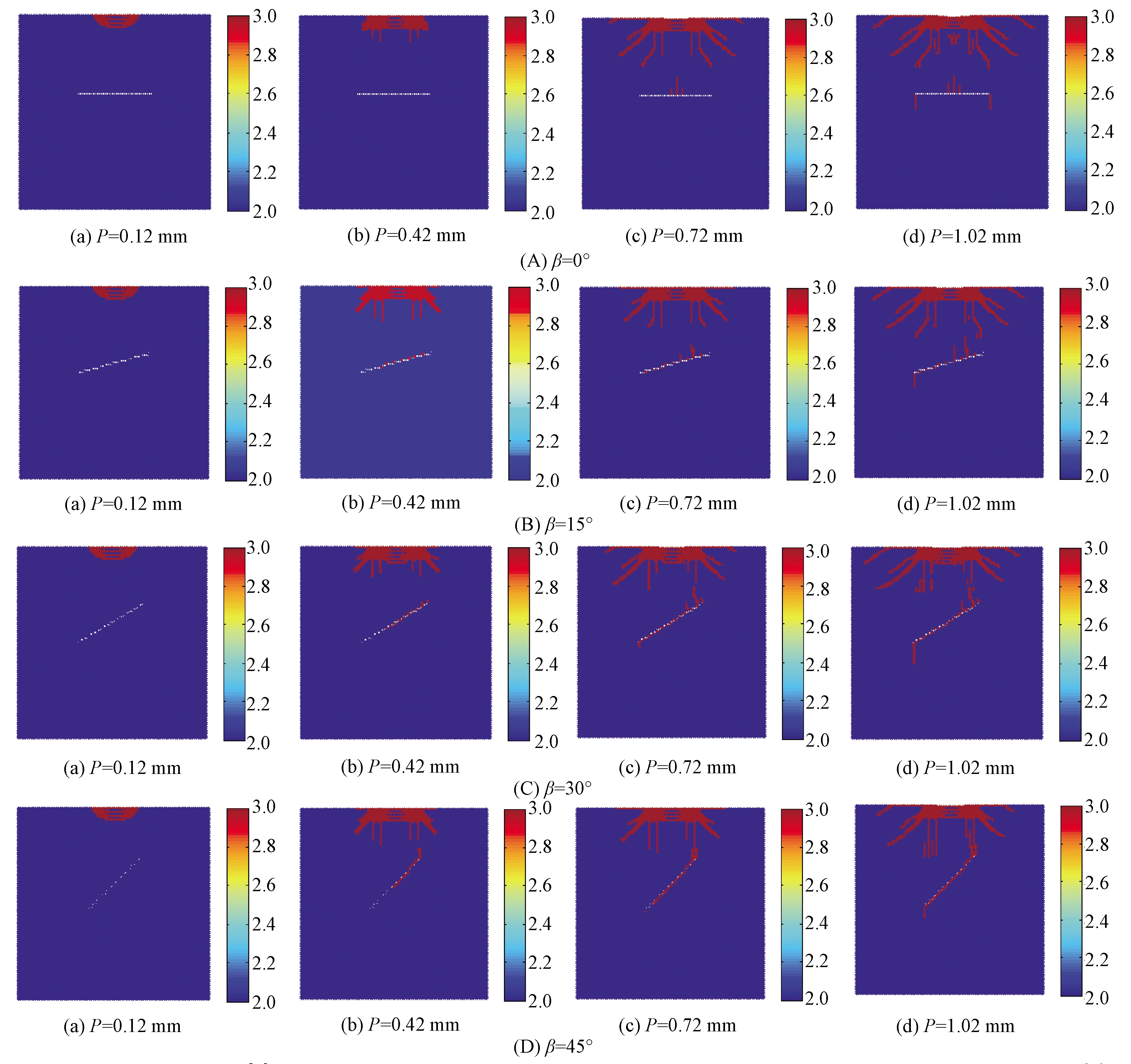
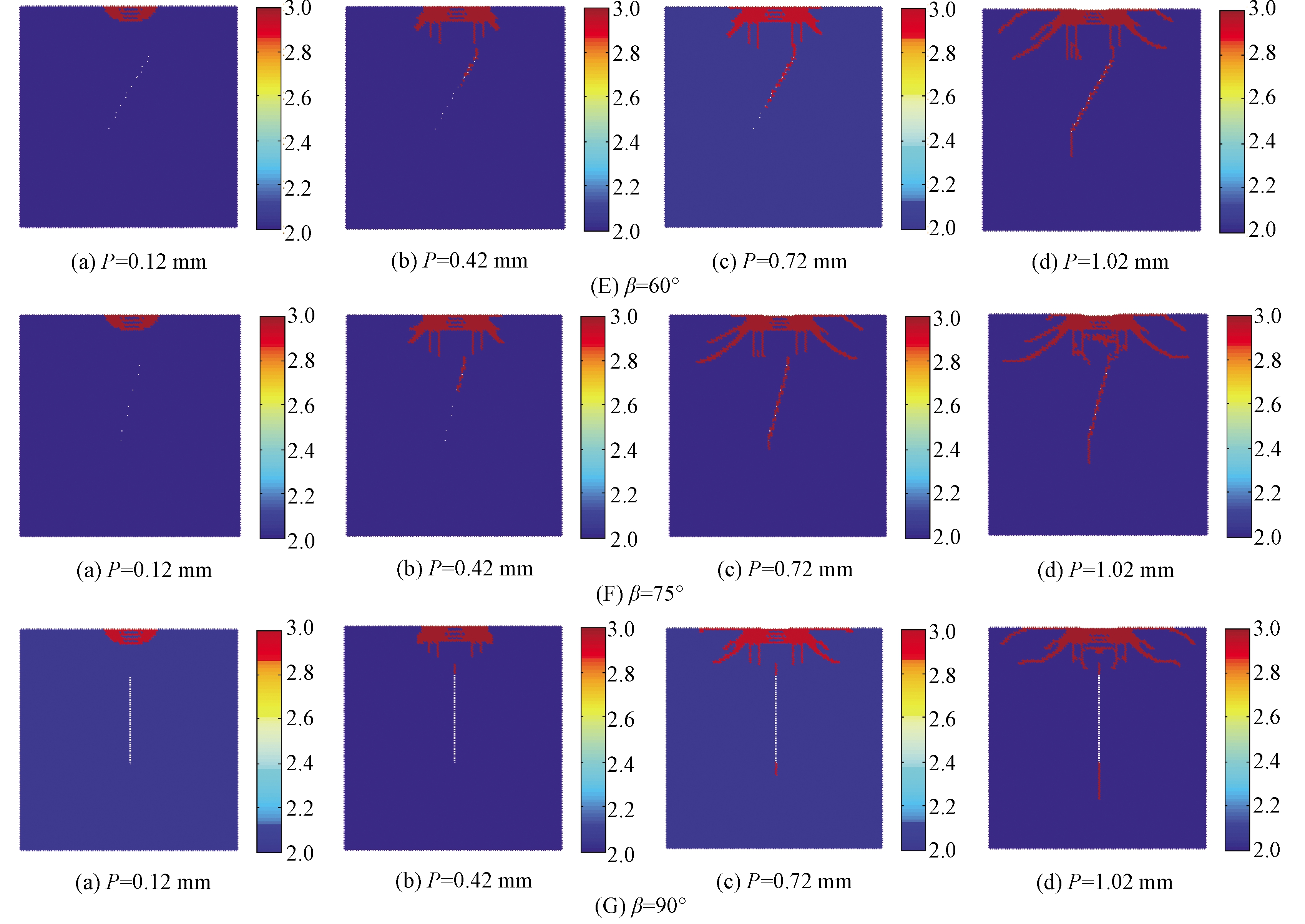
图4 不同断续节理倾角岩体的单滚刀破岩过程
Figue 4 Process of rock fragmentation in rock mass with different joint inclination angle
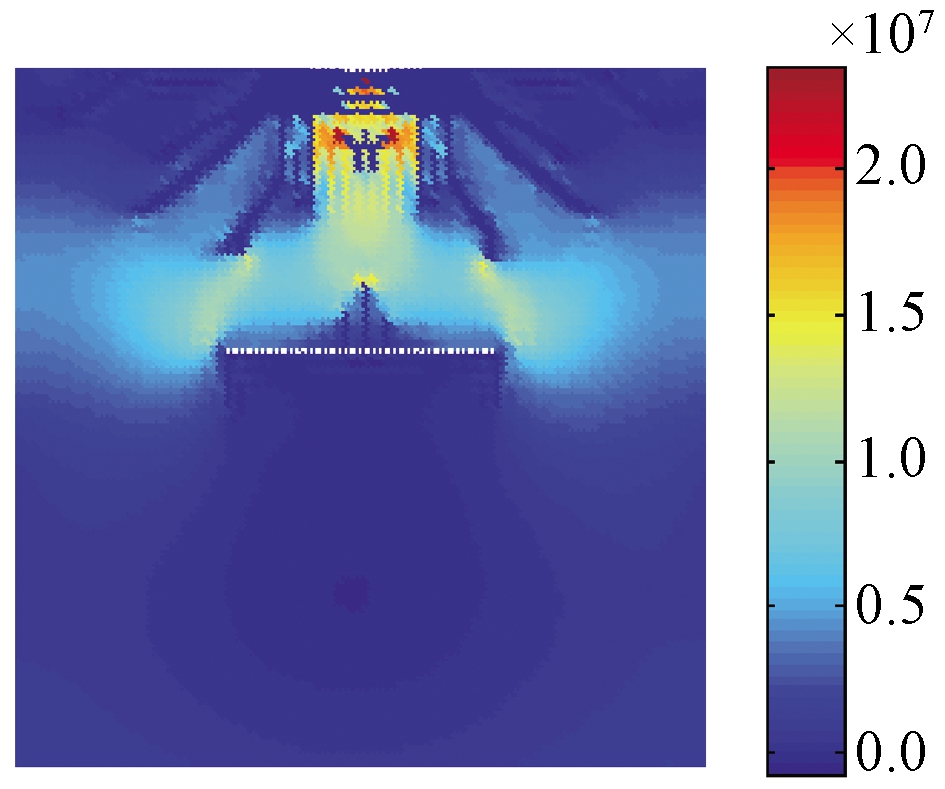
图5 滚刀作用下的最大主应力
Figue 5 Principal stress contour by one cutter
从图4(B)~(F)中的图(d)可以看出:由于模型的不对称性,同一节理倾角时,滚刀左右两侧的赫兹裂纹的扩展深度不相同。对比图4(A)~(G)中的图(d)可以看出:随着节理倾角的增加,赫兹裂纹的扩展深度有较大变化。从图4(A)~(G)可以看出,随着节理倾角β的增加,中央裂纹的扩展长度和扩展方向有较大差异。
3.2 断续节理倾角对裂纹扩展的影响
由图4可以看出,随着断续节理倾角β的增加,中央裂纹扩展方式和扩展长度均有变化。当β≤15°时,中央裂纹向下扩展一段后,改变扩展方向,沿“八”字形扩展,最终两中央主裂纹的水平距离等于断续节理水平宽度,但破岩完成时中央裂纹与断续节理未能连接;当30°≤β≤75°时,中央裂纹向下扩展,最终右侧中央裂纹与断续节理上尖端连接;当β=75°时,中央裂纹向下扩展一段后,停止扩展。随着倾角β的增加,赫兹裂纹的扩展角度基本不变,但其扩展深度却有明显变化,这直接表现为滚刀破岩深度的变化。
为了分析中央裂纹扩展长度和破岩深度的直接影响因素,图6显示了断续节理两端点的位置与中央裂纹长度和破岩深度的关系。随着节理倾角的增加,中央裂纹的扩展长度和节理上端点与加载中心点的距离具有相同的发展趋势;随着节理倾角的增加,左、右侧破岩深度和节理左、右端点与加载面的距离具有相同的发展趋势。
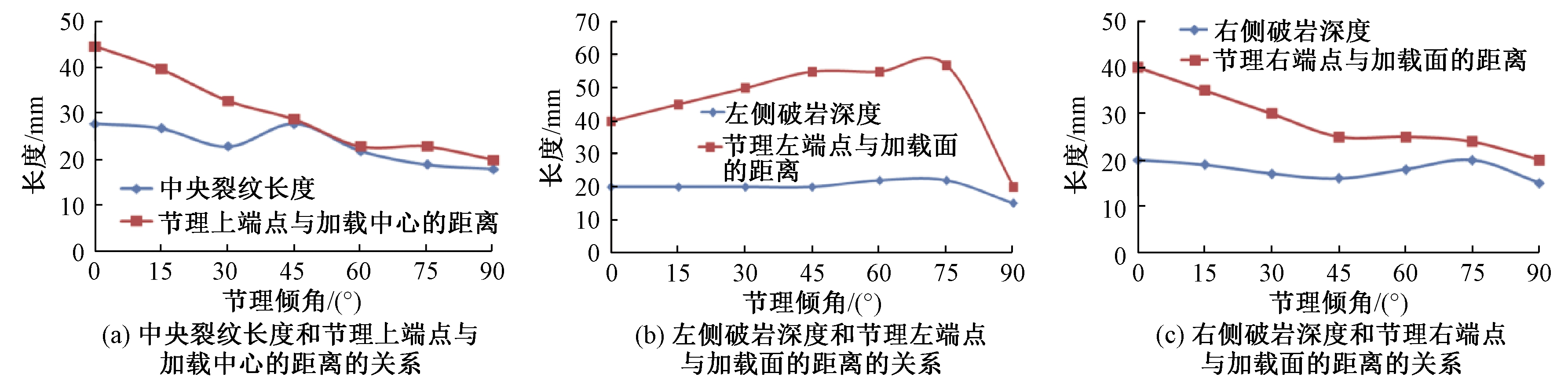
图6 断续节理两端点位置与TBM破岩参数的关系
Figue 6 Relation between the location of endpoints of intermittent joint with parameters of rock fragmentation
3.3 断续节理倾角对破岩效率的影响
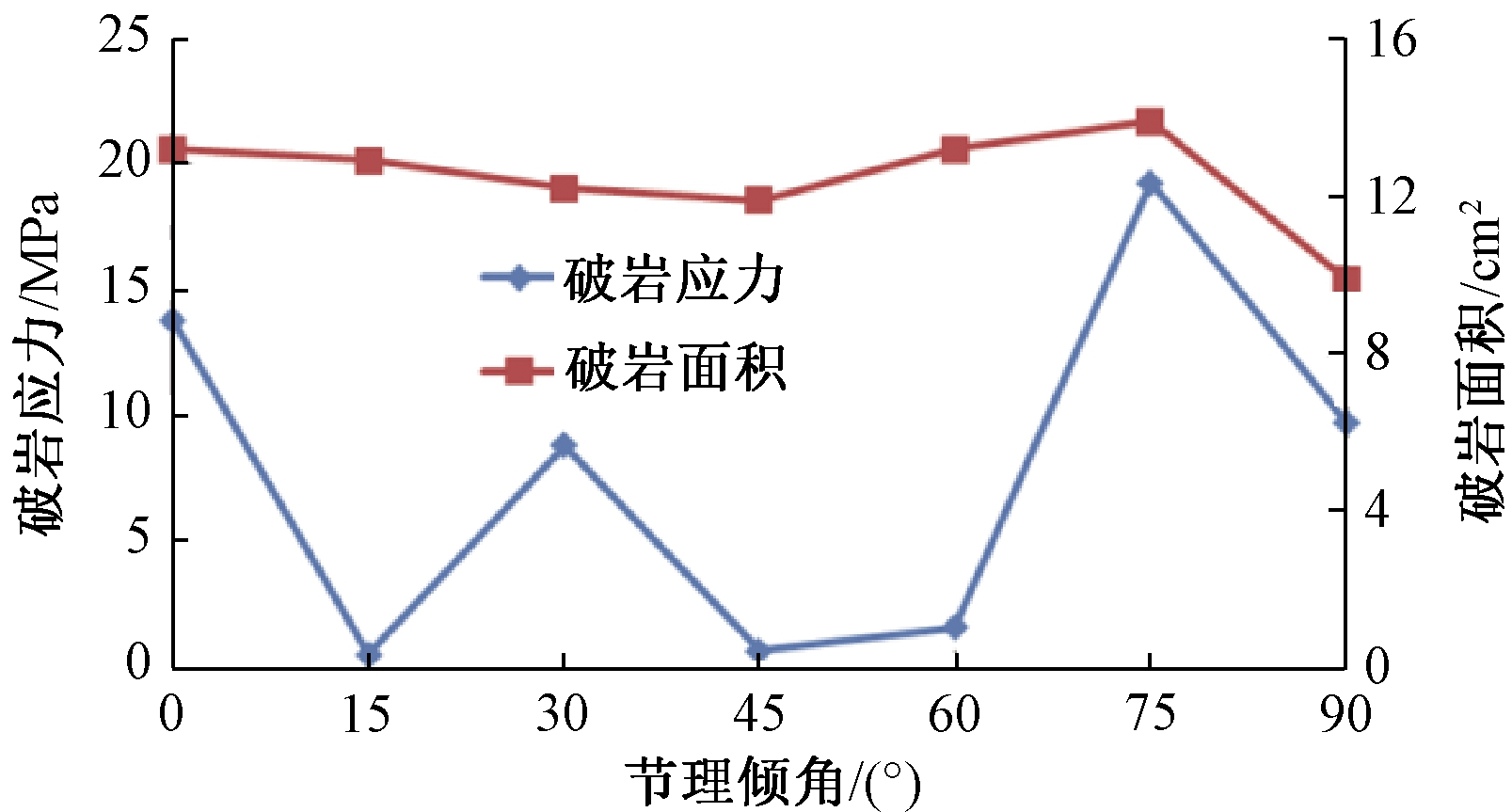
图7 节理倾角与破岩应力、破岩面积之间的关系
Figue 7 Relation between joint inclination angles and the chipping stress and area
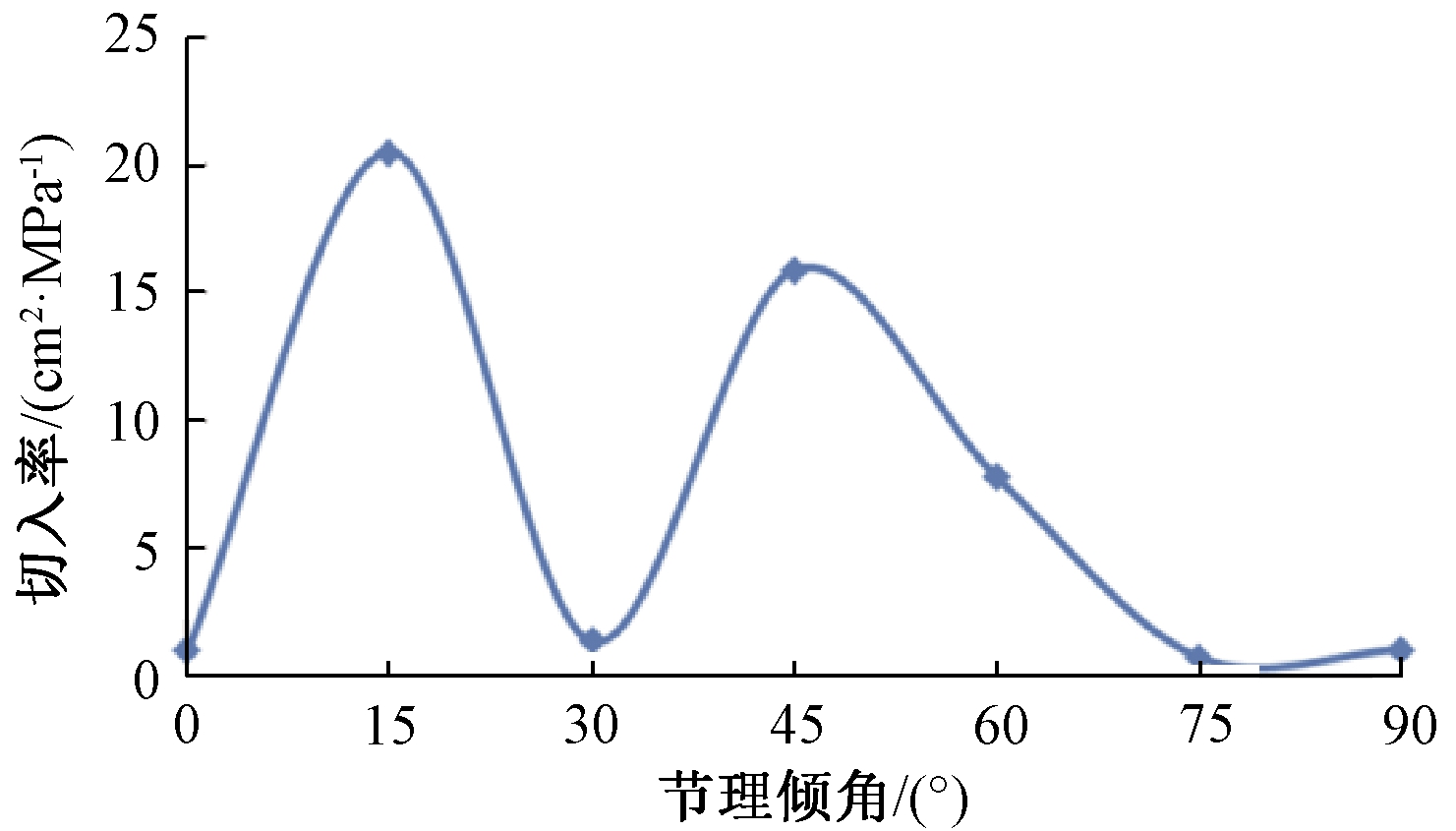
图8 节理倾角与破岩效率之间的关系
Figue 8 Relation between joint inclination angles and the efficiency of rock fragmentation
图7和8显示了随着节理倾角的变化,滚刀破岩力、破岩面积和切入率的变化趋势。图中切入率Pβ=A/σβ,σβ为岩石破碎所需要的最小应力值,A为潜在破岩面积。由图7可知,不同节理倾角时,破岩力出现较大跳动。当β=15°、45°、60°时,破岩力较小,其数值范围为0.63~1.69 MPa;当β=0°、30°、75°、90°时,破岩力较大,变化范围为8.9~19.3 MPa;当β=75°时,破岩力达到最大值19.3 MPa。破岩面积的变化趋势为β从0°~45°时逐渐减小,从45°~75°时逐渐增加,90°时又明显减小。由图8可知滚刀切入率与节理倾角之间的关系。随着β的增加,切入率振动显著。当β=0°、30°、75°、90°时,切入率较小,数值在1附近波动;当β=0°、15°、45°、60°时,切入率较大,最大数值达到20。由此排出以下顺序:P75°<P0°<P90°<P30°<P60°<P45°<P15°,依照此顺序,破岩难度逐渐减小。这与连续节理岩体中,节理倾角对TBM破岩效率的影响截然不同。
4 结论
对含单根断续节理的岩体,中央裂纹的扩展长度和破岩深度的大小与断续节理两端点的位置密切相关。节理尖端越靠近加载面,同时越靠近滚刀加载位置时,节理对中央裂纹和破岩深度抑制作用越大。断续节理倾角对TBM滚刀破岩效率的影响不同于连续节理,滚刀切入率P75°<P0°<P90°<P30°<P60°<P45°<P15°,即按照此顺序破岩难度逐渐减小。
[1] GONG Q M, ZHAO J, JIAO Y Y.Numerical modeling of the effects of joint orientation on rock fragmentation by TBM cutters[J].Tunnelling and underground space technology, 2005,20(2): 183-191.
[2] BEJARI H, HAMIDI J K.Simultaneous effects of joint spacing and orientation on TBM cutting efficiency in jointed rock masses[J].Rock mechanics and rock engineering, 2013,46(4): 897-907.
[3] 邹飞,李海波,周青春,等.岩石节理倾角和间距对隧道掘进机破岩特性影响的试验研究[J].岩土力学, 2012,33(6): 1640-1646.
[4] 谭青,朱逸,夏毅敏,等.节理特征对TBM盘形滚刀破岩特性的影响[J].中南大学学报(自然科学版), 2013,44(10): 4040-4046.
[5] 张银霞,江志强,段留洋,等.TBM盘形滚刀破岩过程的数值研究[J].郑州大学学报(工学版), 2016,37(1): 75-78.
[6] LI K H, CAO P, Liu J.Experimental study of effects of joint on rock fragmentation mechanism by TBM cutters[J].Applied mechanics and materials, 2014,711: 44-47.
[7] 杨圣奇,黄彦华.TBM滚刀破岩过程及细观机理颗粒流模拟[J].煤炭学报, 2015,40(6): 1235-1244.
[8] ZHOU X P, BI J, QIAN Q H.Numerical simulation of crack growth and coalescence in rock-like materials containing multiple pre-existing flaws[J].Rock mechanics and rock engineering, 2015,48(3):1097-1114.
[9] ZHAI S F, ZHOU X P, BI J, et al.The effects of joints on rock fragmentation by TBM cutters using general particle dynamics[J].Tunnelling and underground space technology, 2016, 57:162-172.
[10] 翟淑芳,周小平,毕靖.TBM滚刀破岩的广义粒子动力学数值模拟[J].岩土力学, 2018, 39(7): 2699-2707.
[11] HOEK E, BROWN E T.Empirical strength criterion for rock masses[J].Journal of the geotechnical engineering division, 1980,106(9): 1013-1035.
[12] YIN L J, GONG Q M, MA H S, et al.Use of indentation tests to study the influence of confining stress on rock fragmentation by a TBM cutter[J].International journal of rock mechanics and mining sciences, 2014,72: 261-276.
[13] PANG S S, GOLDSMITH W.Investigation of crack formation during loading of brittle rock[J].Rock mechanics and rock engineering, 1990,23(1): 53-63.