0 引言
在对综合运输系统规划与管理时,忽视不确定因素的影响,可能带来巨大的经济损失.近年来,对于交通系统不确定性的研究逐渐成为热点,涌现于交通工程的各个领域[1-2].交通网络中的不确定性来自3个方面:运输需求的不确定性、运输供给的不确定性以及运输模型内在的不确定性.运输需求的变动性是随机的,例如,具有出行经验的网络使用者更容易识别路径上的非常规状态,而新出行者则受突发事件的影响明显[3].交通运输网络的可靠性概念,建立在系统不确定性的基础上.相关研究始于通信网络,而后逐渐渗透到电力网络、计算机网络、给排水网络等网络系统.近年来,随着交通运输业的迅速发展,人们在追求运输的可达性、时效性的同时,也追求运输系统的可靠性.于是交通网络可靠性方面的研究得到了快速发展.
网络容量概念在运输系统规划与管理过程中扮演了重要的角色.交通网络容量被描述为在预期的服务水平下运输网络系统所能运转的最大需求总量[4].在由多种运输方式构成的综合运输系统中,网络容量表现为某个运输周期内,基于现状的网络运输需求水平,综合运输网络能够承载的最大运输总量,其中考虑:①各运输区段上开行的各类运输服务的最大运输能力(或服务水平);②各运输枢纽内部不同方式之间的中转能力.网络容量模型可用于反映现有状况下系统尚能加载的额外需求.综合运输网络对需求的承载量主要受限于各个基本设施的运输服务能力,这具体是指系统中的枢纽节点设施和线路设施[5].
笔者以定量化分析综合运输网络容量的可靠性为目标,充分反映交通系统中的不确定因素.研究考虑了运输作业过程中的时间和费用成本,构建了运输线路和枢纽上的广义运输费用函数.在此基础上提出基于随机均衡的综合运输网络分配模型及算法,体现了运输企业对运输线路选择的不确定性.假定网络中的需求水平可变,基于储备容量概念[6]提出了综合运输网络容量双层规划模型,体现了运输需求水平的不确定性.最后,借鉴道路系统的网络容量可靠性研究[7],应用蒙特卡洛仿真,对系统中各运输线路、节点设施的运输能力不确定性进行模拟,并结合实际算例评价综合运输网络容量的可靠性.
1 综合运输网络容量模型
1.1 综合运输线路的广义运输费用
(1)物理弧段上的广义运输费用计算公式.为反映不同运输对象对不同运输方式的适应性,本研究采用运输对象的时间价值损耗概念,反映不同品类运输对象的时效性要求.时间价值损耗高的运输对象将选择速度更快的运输方式.d类运输对象沿地理区间a的单位运输成本![]() 通过下式计算:
通过下式计算:
m∈M,d∈D,a∈A,
(1)
式中:κm表示第m种运输方式的单位距离运输成本,元/km;τd为运输对象随时间的价值损耗,元/h;la表示第a个运输区间的距离,km;sm表示第m种运输方式的平均运输速度,km/h.
(2)联运弧段上的运输费用计算公式.枢纽内部不同运输方式之间的联合运输关系,可采用虚拟的联运弧段显性表示,将货(客)运输对象在枢纽处的中转成本换算为广义运输成本,反映了不同方式之间联合运输的时间、经济成本.d类运输对象在枢纽n采用t类联运方式的中转成本为:
d∈D,t∈T,n∈N,
(2)
式中:![]() 表示运输对象在第n个节点采用第t种联运方式的固定成本;
表示运输对象在第n个节点采用第t种联运方式的固定成本;![]() 表示各类货物在节点n处采用第t种联运方式的中转量;
表示各类货物在节点n处采用第t种联运方式的中转量;![]() 代表第t类联运方式的中转时间,考虑了枢纽处的中转运输作业拥挤效应,表示为货(客)流量的增函数,函数形式可根据实际数据标定具体形式.
代表第t类联运方式的中转时间,考虑了枢纽处的中转运输作业拥挤效应,表示为货(客)流量的增函数,函数形式可根据实际数据标定具体形式.
1.2 综合运输网络容量模型及算法
(1)综合运输网络流量分配模型.为构建综合运输网络货流分配模型,将综合运输网络G(N, A)各相关要素的符号定义如下:N表示运输节点集合,n为运输节点编号,A表示运输弧段集合,a为运输弧段编号.弧段a具有方向性,连接相邻两个节点,可表示为(nt, nh),其中,nt是弧段a的上游节点,nh是下游节点.M表示运输方式集合,m为运输方式编号.W表示运输区间的集合,w为运输起讫点区间(OD对)编号.考虑网络中存在多种货流,D表示货流集合,d为货流编号.每种货流的运输需求量已知,表示为![]() 根据文献[8],将综合运输物理网络抽象为引入联运弧的扩展网络,T表示联运模式的集合,t为联运模式编号.
根据文献[8],将综合运输物理网络抽象为引入联运弧的扩展网络,T表示联运模式的集合,t为联运模式编号.
对于每种货流需求存在若干条备选路径连接运输起点和终点,定义![]() 表示OD对之间运输d货流的路径集合,其中第k条路径
表示OD对之间运输d货流的路径集合,其中第k条路径![]() 上的运量表示为
上的运量表示为![]() 综合运输网络分配问题就是在OD对之间的货流需求
综合运输网络分配问题就是在OD对之间的货流需求![]() 已知的条件下,确定各路径上的货流运输量
已知的条件下,确定各路径上的货流运输量![]()
因此,综合运输网络运量分配模型表示为以下数学规划问题:
(3)
![]() ∀w∈W,d∈D;
∀w∈W,d∈D;
(4)
(5)
(6)
![]() ∀t∈T,n∈N;
∀t∈T,n∈N;
(7)
(8)
式中:![]() 为路段a上第m种运输方式的总运量;
为路段a上第m种运输方式的总运量;![]() 为第a个运输区间上第m种运输方式对第d种货物的运量;
为第a个运输区间上第m种运输方式对第d种货物的运量;![]() 表示运输弧段a上运输方式m与运输路径的关联系数,当w之间路径k上的货流d经过路段a并使用第m种运输方式时,
表示运输弧段a上运输方式m与运输路径的关联系数,当w之间路径k上的货流d经过路段a并使用第m种运输方式时,![]() ,否则为0;
,否则为0;![]() 为节点n处第t种联运方式的中转运量;
为节点n处第t种联运方式的中转运量;![]() 为联运弧段与运输路径的关联系数,当w之间路径k上的货流d通过节点n上的t种联运方式时,
为联运弧段与运输路径的关联系数,当w之间路径k上的货流d通过节点n上的t种联运方式时,![]() 否则为
否则为![]() 为运输弧上采用第m种方式运输1单位d货物的广义费用,与路径运输量
为运输弧上采用第m种方式运输1单位d货物的广义费用,与路径运输量![]() 无关,由式(1)求出.此外,用
无关,由式(1)求出.此外,用![]() 表示OD对之间第k条路径上d货物的广义运输费用,采用如下公式计算:
表示OD对之间第k条路径上d货物的广义运输费用,采用如下公式计算:
(9)
通过构造上述数学规划的拉格朗日函数,易证该数学规划问题的解服从Logit选择模型.证明略.
(2)综合运输网络流量分配算法.为求解上述综合运输网络容量模型,笔者将综合运输服务网络中的运量分配过程分为两个阶段:首先,确定各OD对不同货流的可行运输路径集,采用K最短路径方法[9];其次,基于给定路径集合,应用前面给出的综合运输网络流量分配模型,进行运量分配,具体实现如下.
步骤1:根据综合运输网络中的运输弧段与枢纽联运方式,应用节点拆分法将原网络转换为拓展网络,并输入运输网络基本属性.
步骤2:根据网络拓扑和初始权重进行K最短路径搜索,生成各货流d的OD可行路径集![]()
步骤3:初始化路段运量,令![]() 对不同OD对之间的各类货流d,计算运输弧段的广义费用
对不同OD对之间的各类货流d,计算运输弧段的广义费用![]() 与联运弧段的广义费用
与联运弧段的广义费用![]() ;对各类货流d的可行运输路径,初始化各路径费用
;对各类货流d的可行运输路径,初始化各路径费用![]() 令i:=0(冒号为对左侧变量赋值,用于算法循环).
令i:=0(冒号为对左侧变量赋值,用于算法循环).
步骤4:对每个OD对之间的各类货流d,通过以下Logit分配模型计算路径运量,
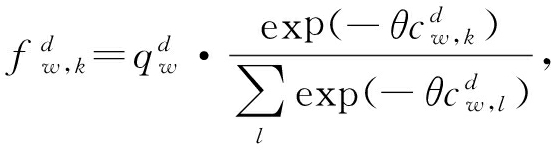
∀![]()
w∈W,d∈D.
步骤5:由路径运量![]() 计算运输弧段的辅助运量
计算运输弧段的辅助运量![]() 和联运弧段的辅助运量
和联运弧段的辅助运量![]()
∀m∈M,a∈A;
![]() ∀t∈T,n∈N.
∀t∈T,n∈N.
步骤6:更新路段运量,
![]() ∀m∈M,a∈A;
∀m∈M,a∈A;
![]() ∀t∈T,n∈N.
∀t∈T,n∈N.
步骤7:更新路段广义费用![]() 和
和![]()
步骤8:更新路径费用![]()
步骤9:收敛性检验,如果路段运量的相对误差满足给定的收敛精度ε,
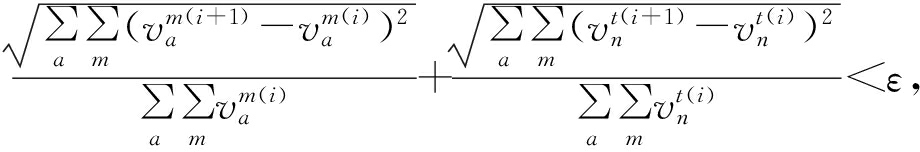
则算法停止;否则,返回步骤4,并令i:=i+1.
(3)综合运输网络容量模型及评估方法.借鉴道路网络储备容量模型[10],综合运输网络容量模型可表示为如下双层规划问题:
(10)
![]() ∀a∈A,m∈M;
∀a∈A,m∈M;
(11)
![]() ∀n∈N,t∈T.
∀n∈N,t∈T.
(12)
式(10)~(12)表示的上层问题中,![]() 为第a个运输弧上第m种运输方式的输送能力;
为第a个运输弧上第m种运输方式的输送能力;![]() 为第n个运输结点上第t种联运方式的中转能力
为第n个运输结点上第t种联运方式的中转能力![]() 和
和![]() (μ)的函数关系由式(3)~(8)所定义的下层数学规划问题给出.
(μ)的函数关系由式(3)~(8)所定义的下层数学规划问题给出.
2 综合运输网络容量可靠性分析
2.1 综合运输网络容量可靠性评价流程
笔者采用蒙特卡罗仿真来模拟设施服务能力的不确定因素,即各独立弧段的容量随机变化情况,进而计算整个运输网络容量的可靠性结果.具体步骤如下.
步骤1:初始化参数,给定运输网络各弧段容量的分布特征![]() ;初始的预期运输能力θD和运输能力的变化量ΔθD;仿真样本量I;设置样本数i:=1.
;初始的预期运输能力θD和运输能力的变化量ΔθD;仿真样本量I;设置样本数i:=1.
步骤2:根据初始化的容量分布特征,生成各弧段容量随机数![]()
步骤3:根据生成的随机数,运用1.2节中的网络容量模型求解综合运输网络容量.
步骤4:记录第i个样本的计算结果.
步骤5:如已经生成的样本数i小于预设样本量I,则增加样本数量,令i:=i+1并返回步骤2;否则进入步骤6.
步骤6:计算运输网络的容量可靠性结果.
步骤2采用了Chang等[11]提出的随机变量产生过程来产生网络容量随机数,是蒙特卡罗模拟的一种常用方法.这种方法可以用于产生多元、非正态、具有相关性的随机变量.随机变量的通用产生过程参考文献[5].对于每次蒙特卡罗的模拟值,都需要计算运输网络保留容量,在步骤4中,各种统计值(各种货物的路段货运量、中转货运量、路径货运量、路网最大运输量、各弧段饱和度等)均需要收集,用于在步骤6中来计算综合运输网络容量的可靠性.需要说明的是,上述方法产生的随机容量结果仅是服从预定均值和协方差的随机变量,并不严格限定为正态分布(即非正态).
2.2 综合运输网络容量可靠性评价的算例分析
考虑图1所示的综合运输网络,网络包含13个运输弧段,4种运输方式(即公路、铁路、水运、航空),8个运输节点,其中5个节点为枢纽点.4种运输方式的平均运输速度与单位距离运价如表1所示.网络中各运输弧段的实际运输距离如表2所示.各运输节点提供相应的不同方式之间的联运服务,其可行的联运形式由枢纽点的前趋弧段与后继弧段上的运输方式确定,中转运输的参数设定如图2所示.假定货流在枢纽中转过程中的延误时间函数采用以下具体形式:
(13)
式中:![]() 为该结点联运方式t的最大中转能力;
为该结点联运方式t的最大中转能力;![]() 为最小中转作业时间.
为最小中转作业时间.
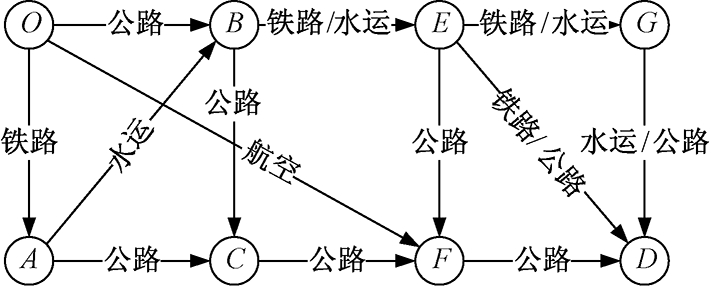
图1 综合运输网络实例图
Fig.1 An example of comprehensive transportation network
表1 综合运输网络中各运输方式属性
Tab.1 Features for transportation modes in comprehensive transportation network
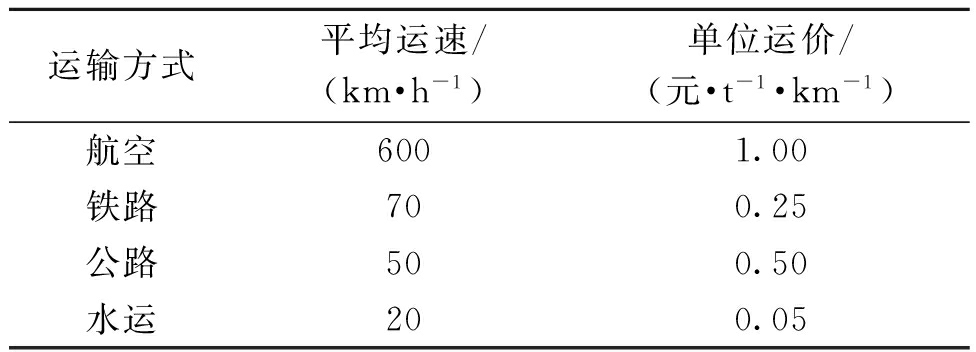
运输方式平均运速/(km·h-1)单位运价/(元·t-1·km-1)航空6001.00铁路700.25公路500.50水运200.05
表2 综合运输网络中各运输区间属性
Tab.2 Characteristics of transport links in the comprehensive transportation network
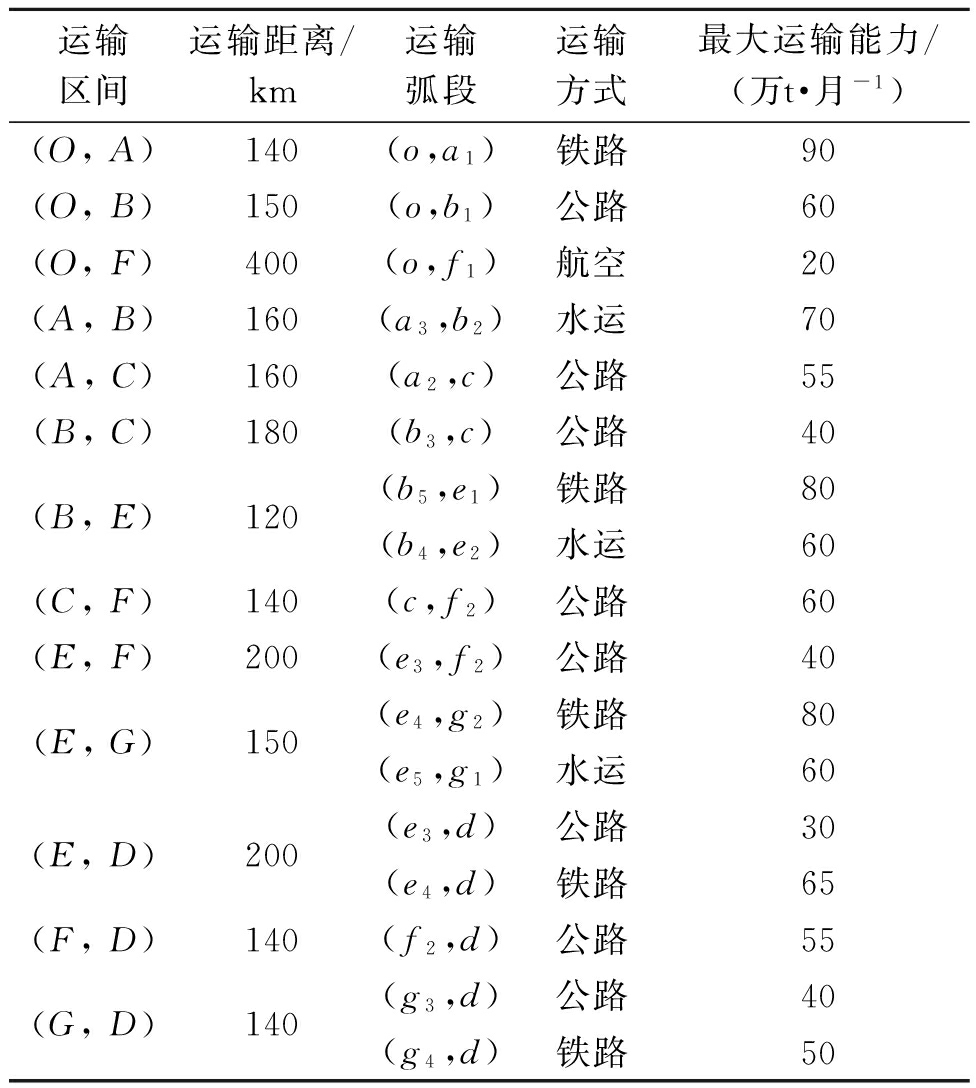
运输区间运输距离/km运输弧段运输方式最大运输能力/(万t·月-1)(O,A)140(o,a1)铁路90(O,B)150(o,b1)公路60(O,F)400(o,f1)航空20(A,B)160(a3,b2)水运70(A,C)160(a2,c)公路55(B,C)180(b3,c)公路40(B,E)120(b5,e1)铁路80(b4,e2)水运60(C,F)140(c,f2)公路60(E,F)200(e3,f2)公路40(E,G)150(e4,g2)铁路80(e5,g1)水运60(E,D)200(e3,d)公路30(e4,d)铁路65(F,D)140(f2,d)公路55(G,D)140(g3,d)公路40(g4,d)铁路50
考虑网络中的运输区间为起点O到终点D,(O, D)之间存在3种运输货流,运输需求量分别为![]() 万t/月,
万t/月,![]() 万t/月,
万t/月,![]() 万t/月;其货物价值随运输时间价值分别为τ1=1.0元/h,τ2=20.0元/h,τ3=100.0元/h,即时间价值越高,对运输时间的要求越紧急.
万t/月;其货物价值随运输时间价值分别为τ1=1.0元/h,τ2=20.0元/h,τ3=100.0元/h,即时间价值越高,对运输时间的要求越紧急.
首先采用节点拆分方法,可将图2中的网络在枢纽节点处进行拆分,增加相应的虚拟弧段和虚拟节点,得到图2所示的扩展运输网络.为便于表述,对各弧段进行编号(如图2).区间弧段上的运输能力和中转能力的分布区间依据表2和表3所示的最大运输(中转)能力上下浮动10个单位.为了方便起见,假设容量之间的协方差矩阵为0,运输容量、中转容量之间均不相关.采用上一节介绍的方法,共生成了500组路段容量和中转容量随机数.
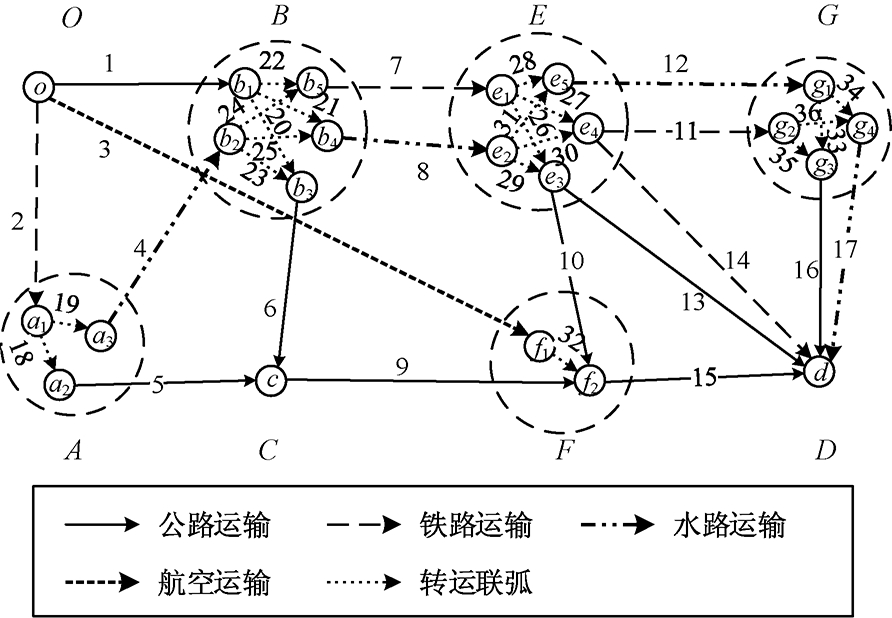
图2 扩展后的运输网络及编号
Fig.2 Expanded transportation network with indices
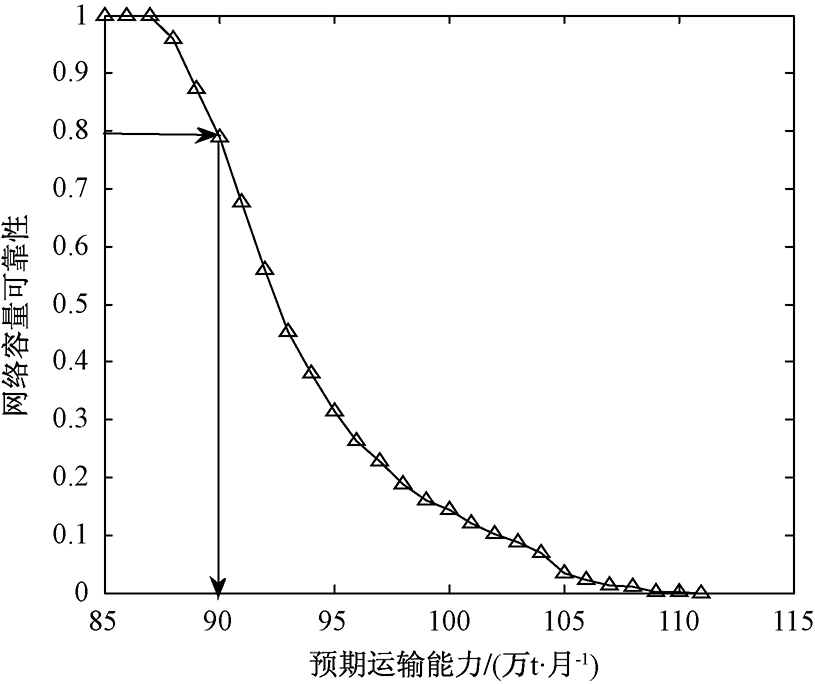
图3 网络容量可靠性随不同预期货运能力变化
Fig.3 Capacity reliability for different expected values
综合运输网络容量可靠性评估通过这500组随机容量值演化过程来计算,结果如图3所示.可以发现该运输网络容量能力上限为110.25万t/月,下限为87.85万t/月,即当预期货运能力小于等于87.85万t/月时,系统是100%可靠的;随着预期货运能力的提高,网络容量可靠性逐渐减小;而当预期运输能力大于等于110.25万t/月,系统将完全不可靠.在80%可靠性的情况下,综合运输网络达到90万t/月的货运能力.
表3 各运输枢纽内联运弧段的属性
Tab.3 Characteristics of transfer links in transport hubs
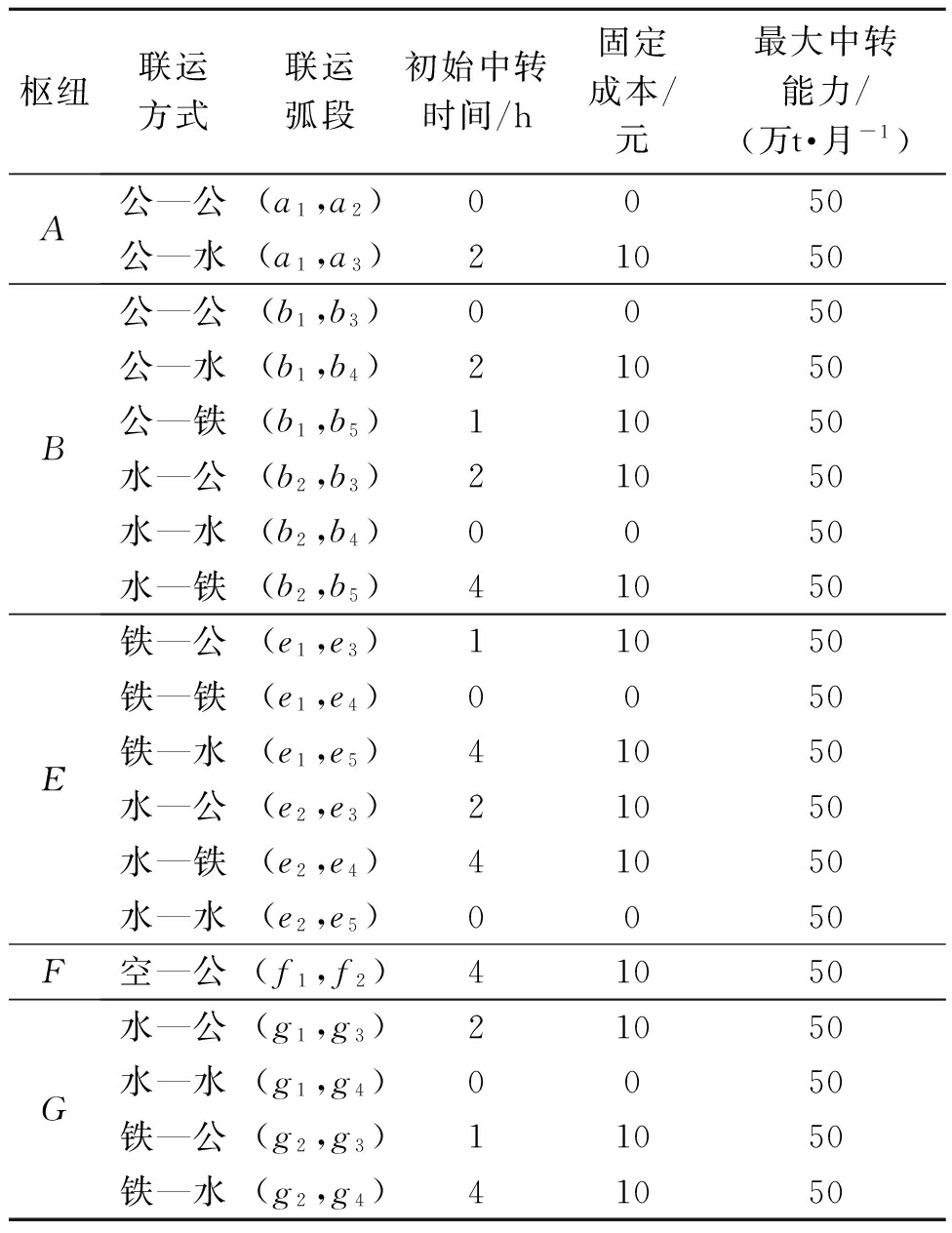
枢纽联运方式联运弧段初始中转时间/h固定成本/元最大中转能力/(万t·月-1)A公—公(a1,a2)0050公—水(a1,a3)21050B公—公(b1,b3)0050公—水(b1,b4)21050公—铁(b1,b5)11050水—公(b2,b3)21050水—水(b2,b4)0050水—铁(b2,b5)41050E铁—公(e1,e3)11050铁—铁(e1,e4)0050铁—水(e1,e5)41050水—公(e2,e3)21050水—铁(e2,e4)41050水—水(e2,e5)0050F空—公(f1,f2)41050G水—公(g1,g3)21050水—水(g1,g4)0050铁—公(g2,g3)11050铁—水(g2,g4)41050
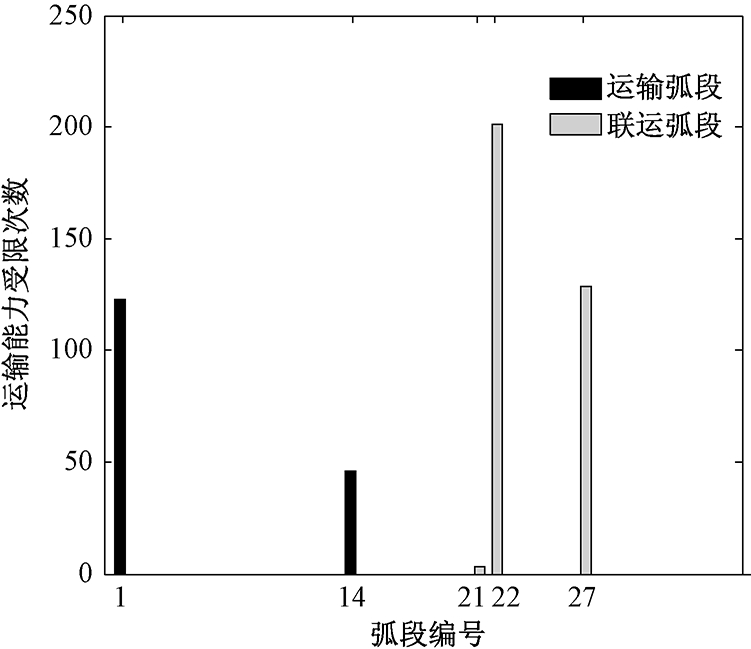
图4 运输能力受限的弧段统计分析
Fig.4 Times of links constrained by capacities
为进一步分析影响网络容量提高的关键弧段有哪些,图4给出了容量受限的弧段的统计分析结果.在500次模拟过程中,弧段1、14、21、22、27的饱和度会达到1.0,因而这些弧段的容量有待提高.其中弧段22和27均位于货物中转枢纽,达到饱和的频次最高,可见枢纽在综合运输网络中占据重要的地位,它影响着网络运输能力的提高.
最后,笔者对弧段22和弧段27上的运量和容量进行统计分析,具体如图5和图6所示.图5和图6再现了不确定环境下交通设施运量和容量的关系.可以发现,这两条弧段的运量和容量均有重叠,因而这两条弧段自身的运输能力(即容量)会影响综合运输网络总体容量的提高.相比于弧段27,弧段22的运量和容量频次重叠部分更多,且运量和容量的累计概率分布曲线更为接近.因此说明,弧段22对整个综合运输网络容量更具影响力.通过定量化分析设施运量和容量频次的关系,可以有效地帮助决策者识别运输网络中的关键区间.

图5 弧段22货运量和容量统计分析
Fig.5 Distributions of link capacity and link flow on link 22
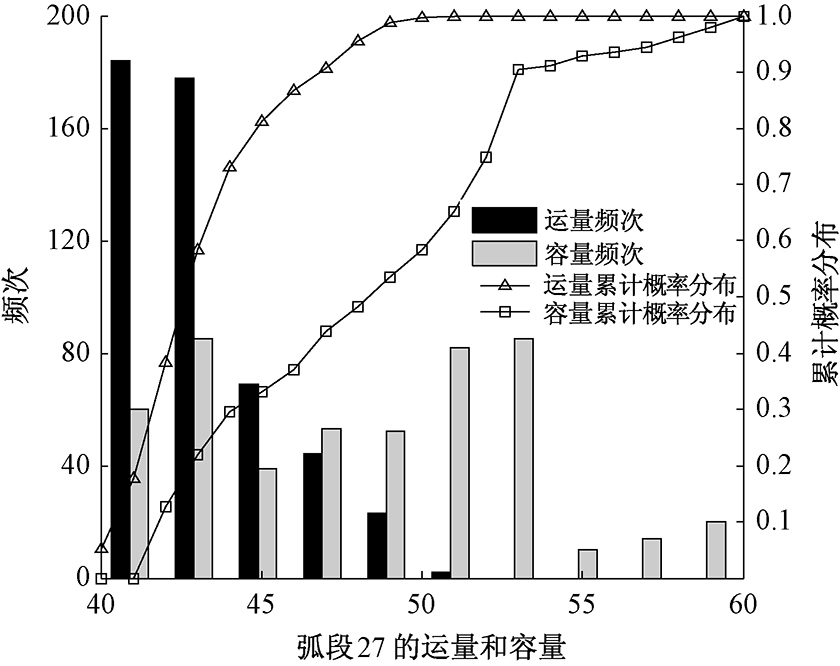
图6 弧段27货运量和容量统计分析
Fig.6 Distributions of link capacity and link flow on link 27
3 结论
笔者针对综合运输系统总体运输能力这一问题,考虑系统运行过程中来自内部和外部的不确定因素,对综合运输网络的容量可靠性评价提出了具体的分析模型与方法.为此,定义了广义运输费用并提出了用于多方式多用户的综合运输网络分配模型及算法.并且借鉴道路交通网络容量可靠性分析框架,提出了用于综合运输系统的容量可靠性分析方法.结合实例,验证了所提出可靠性分析方法的有效性.通过该综合运输网络的容量可靠性进行评估,可以发现枢纽点中转能力对整个网络可靠性有重要的影响作用.本研究从综合运输网络系统的宏观角度为交通运输管理部门的决策工作提供了有效的数学工具.
参考文献:
[1] 杨高飞,徐睿,秦鸣,等.基于ARMA和卡尔曼滤波的短时交通预测[J].郑州大学学报(工学版), 2017, 38(2): 36-40.
[2] 常玉林,汪小渟,张鹏.改进蚁群算法在交通分配模型中的应用[J].郑州大学学报(工学版), 2017, 38(2): 41-44.
[3] Al-DEEK H, EMAM E B. New methodology for estimating reliability in transportation networks with degraded link capacities[J]. Journal of intelligent transportation systems, 2006, 10(3): 117-129.
[4] 刘兰芬,杨信丰,李引珍,等. 基于服务水平下用户均衡的交通网络容量研究[J]. 兰州交通大学学报, 2012, 31(6): 108-113.
[5] 朱森来,程琳,许项东.基于储备容量的交通网络潜在瓶颈路段识别[J]. 系统工程理论与实践, 2014, 34(6): 1572-1577.
[6] 杨超,蒲琪,涂颖菲.交通需求组合模型的不确定性分析[J]. 同济大学学报(自然科学版), 2010, 38(1): 58-64.
[7] CHEN A, YANG H, HONG K L, et al. Capacity reliability of a road network: an assessment methodology and numerical results[J]. Transportation research part B: methodological, 2002, 36(3): 225-252.
[8] 郑长江,高正平.区域货物综合运输网络容量可靠性分析[J]. 大连交通大学学报, 2012, 33(2): 32-36.
[9] 段宗涛, WANG W X, 康军, 等. 面向城市交通网络的K最短路径集合算法[J]. 交通运输系统工程与信息, 2014, 14(3): 194-200.
[10] KASIKITWIWAT P, CHEN A. Analysis of transportation network capacity related to different system capacity concepts[J]. Journal of the eastern asia society of transportation studies, 2005,6: 1439-54.
[11] CHANG C, TUNG Y, YANG J. Monte Carlo simulation for correlated variables with marginal distributions[J]. Journal of hydraulic engineering, 1994, 120(3): 313-331.