0 引言
铁水含硫量直接影响钢材的韧性、塑性和抗疲劳等性能,铁水预脱硫是生产优质钢的重要环节.KR机械搅拌法因设备简单、可操作性强和脱硫效率高等优势被广泛应用于钢铁行业[1-2].目前,冶金工作者主要通过热态实验和水模实验研究搅拌器结构和工艺参数等对脱硫效果和混合时间的影响,以确定最优的参数组合[3-5].Nakai等[6-7]利用水模试验研究了不同转速和搅拌器安装位置下液面漩涡深度对脱硫剂分散的影响.Busciglio和Brucato等[8-9]通过试验数据拟合预测了搅拌桨转速、装液高度和搅拌桨离底高度对搅拌效果的影响.与试验方法相比,数值仿真具有更加经济、高效和直观的特点.党林贵等[10]采用Fluent软件对3种组合桨搅拌器在搅拌槽内的流动混合特性进行了数值模拟.Yeoh等[11-14]利用多重坐标系法和欧拉-欧拉多相流模型解决搅拌槽内的流场运动及分散悬浮问题.在实际KR机械搅拌脱硫过程中,密度较小的脱硫剂大量漂浮在铁水表面,搅拌作用形成的流场可以将内部铁水输送到表面与脱硫剂反应.此外,受漩涡卷吸作用进入流场内部的脱硫剂也能在流场的带动下与内部铁水充分反应.目前,专家学者在对搅拌槽流场特性进行数值模拟时,一方面假设自由液面为对称边界面,忽视了液面漩涡对脱硫剂混合的影响,另一方面将脱硫剂视为拟流体,无法直观显示颗粒在内部流场的运动情况.采用DPM方法对大量脱硫剂颗粒运动轨迹跟踪以及考虑液面对颗粒分散状态影响的数值研究鲜有报道.因此,研究搅拌罐内不同工况下的流场和自由液面对脱硫剂分散的影响具有重要意义.
1 数值建模
1.1 几何模型及相关参数
由于高温铁水的热态实验条件苛刻且会造成一定的危险,而冷态水易于操作,且其在20 ℃时的运动黏度与1 600 ℃铁水的运动黏度相当,保证了运动学相似,故用水模实验代替热态铁水实验.笔者建立的水模试验模型是在几何相似前提下,将实际工况下的搅拌罐和搅拌器模型按照1∶8的比例进行缩小,具体水模试验装置如图1所示,搅拌罐与搅拌器的尺寸及相关工艺参数如表1所示.在电机带动下,将十字形搅拌器插入平底搅拌罐中.水模试验在目前的铁水脱硫研究中应用广泛,且能够为真实的铁水脱硫分析提供指导和借鉴意义.为了验证数值模型的正确性,建立与试验模型相同的搅拌罐与搅拌器几何模型,如图2所示.

图1 水模试验装置
Fig.1 Water model experimen
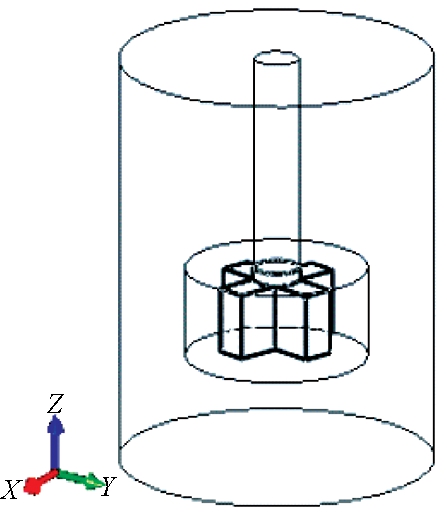
图2 搅拌罐与搅拌器几何模型
Fig.2 Stirred vessel and stirrer model
表1 搅拌罐与搅拌器相关尺寸及工艺参数
Tab.1 Related sizes and parameters of stirred vessel and stirrer

搅拌罐搅拌器脱硫剂颗粒高度/mm直径/mm液深/mm高度/mm直径/mm叶宽/mm浸入深度/mm转速/(r·min-1)直径/mm密度/(kg·m-3)69552341411020352214,276,338160,240,320130
1.2 计算区域分割和网格划分
根据多重坐标系法将搅拌罐分割为动、静两个区域,其中包含搅拌器的动区域采用旋转参考系,槽体周围的静区域采用静止参考系,动、静区域划分如图3所示.两区域的界面为相互作用面,假定通过该界面的流动为稳态的,通过相互作用面进行流场计算数据的交换.利用ICEM软件分别对动、静区域进行网格划分,如图4所示.
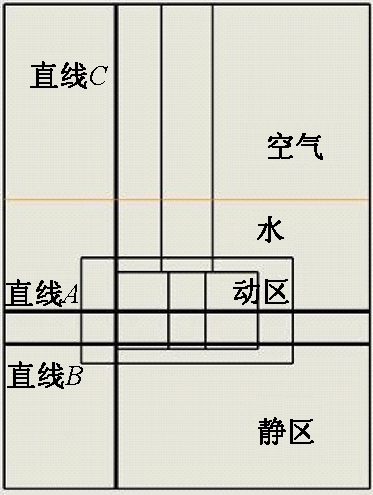
图3 动、静区域划分
Fig.3 Dynamic and static zone

图4 搅拌罐网格图
Fig.4 Diagram of stirred vessel grid
两区域均采用欧拉三维网格,其中静区域网格划分采用六面体结构单元,动区域网格划分采用四面体非结构单元,动区域网格设置较静区域网格细密,网格数量为20万左右.通过改变网格密度验证网格独立性,在节省计算成本的前提下,该网格划分的数量和质量均满足搅拌器仿真的精度要求.
1.3 边界条件和数值算法设置
初始时搅拌罐内的水和空气都处于静止状态,气液交界面为水平面,利用Adapt Region分别设置液体和气体区域.采用DPM方法在搅拌罐顶部产生1 200个颗粒.将搅拌罐壁面定义为无滑移壁面边界条件,近壁区采用标准壁面函数.将位于静区域中的搅拌轴定义为运动壁面边界条件,其绝对转速与动区域网格相同.将动区域搅拌器壁面定义为运动壁面边界条件,其相对转速设为零,即搅拌器与动区域网格同步旋转.气相上表面定义为压力出口.将动静区域的接触面定义为interface交界面.笔者使用标准κ-ε湍流模型描述流场的湍流特性,采用VOF法捕捉KR法铁水搅拌过程中的自由液面.使用SIMPLE算法进行压力-速度耦合,差分运算统一采用一阶迎风格式,各项收敛残差设为10-3,时间步长设为0.001 s.在数值模拟时,待残差稳定后输出变量结果.
2 仿真结果及分析
2.1 模型验证
通过在水模试验中的搅拌罐侧壁竖立标尺,得到漩涡高度和深度的测量结果,并与数值模拟结果进行比较.图5和图6分别为水模试验和数值模拟得到的漩涡深度及高度随转速变化图.从图5和图6可以看出,数值模拟和水模试验得到自由液面漩涡深度和漩涡高度结果基本一致,其中两者的漩涡深度最大相对误差仅为3.1%,漩涡高度最大相对误差仅为6.5%.通过与试验结果的对比可知,利用该数值模型对KR法搅拌罐内流场及自由液面进行数值模拟是可行的.
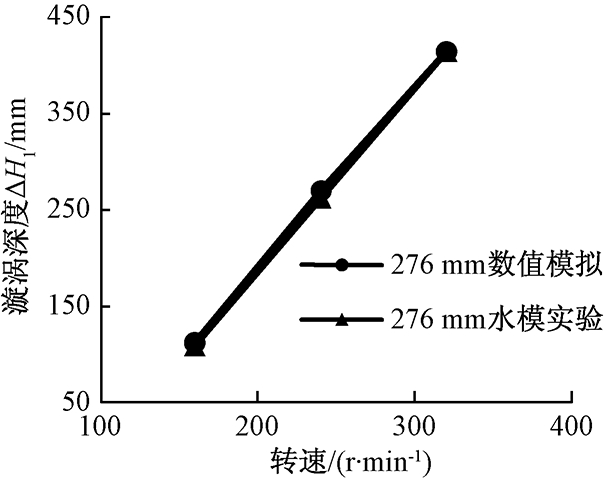
图5 水模试验与数值模拟漩涡深度结果对比
Fig.5 Comparison of vortex depth from water model experiment and numerical simulation
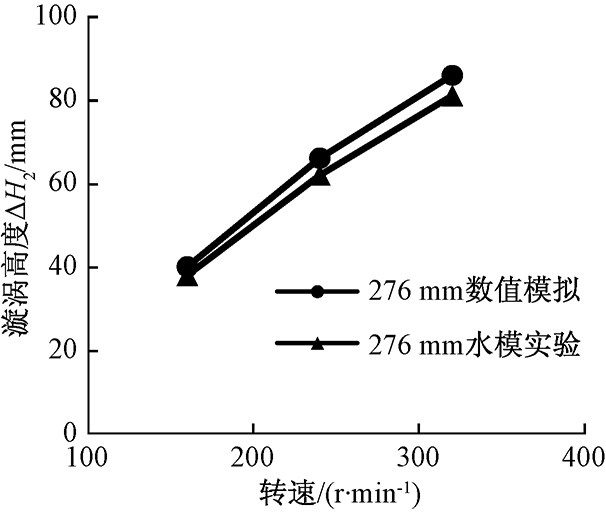
图6 水模试验与数值模拟漩涡高度结果对比
Fig.6 Comparison of vortex height from water model experiment and numerical simulation
2.2 流速场模拟结果
图7为数值模拟得到的XOZ截面流速场矢量云图.由图7可以看出,最大速度位于叶轮端部,且沿着搅拌罐壁方向,速度逐渐降低.搅拌罐壁附近和叶轮正下方速度较小,容易出现流动死区,不利于物料的混合.从流迹线可以看出,在搅拌过程中,搅拌器周围流体沿叶径向罐侧壁流动,在侧壁位置处分流形成向上流动和向下流动两部分,向上流动的流体受到压差和重力等作用,形成返回叶轮上方的环流,而向下运动的流体在压差作用下形成叶轮下方的环流.返回的流体在搅拌作用下形成上下两部分循环运动.由于流体流动是关于搅拌轴对称分布的,罐内形成4股循环流动,这种流场分布特点有助于物料随流体输运至流场内部,实现充分的混合和反应.
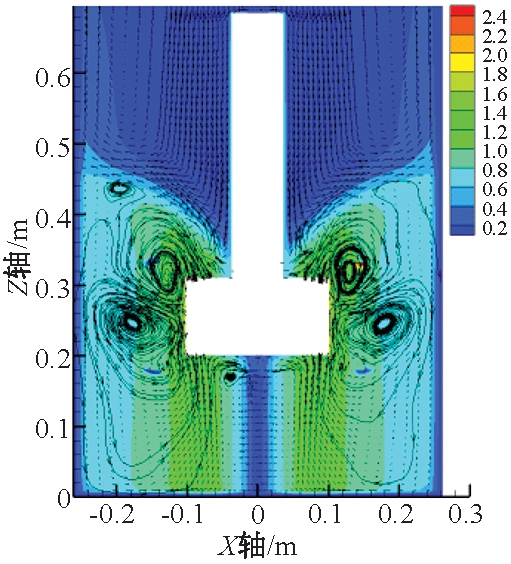
图7 XOZ截面流速场矢量云图
Fig.7 Vector contour of velocity field on XOZ section
2.3 转速对流速场的影响
为衡量不同转速下流场径向和轴向速度分布,在图3上选取XOZ截面上直线A和直线C.直线A过搅拌器几何中心,直线C过搅拌器叶轮端部.图8和图9分别是不同转速下搅拌罐内部流场径向速度和轴向速度分布曲线.
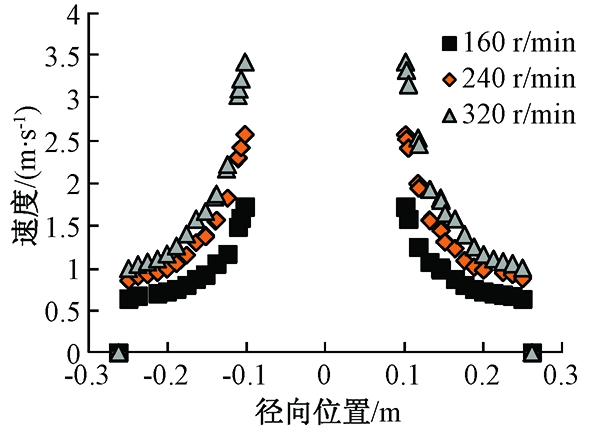
图8 不同转速下径向速度分布曲线
Fig.8 Diagram of radial velocity distribution under different stirring speeds
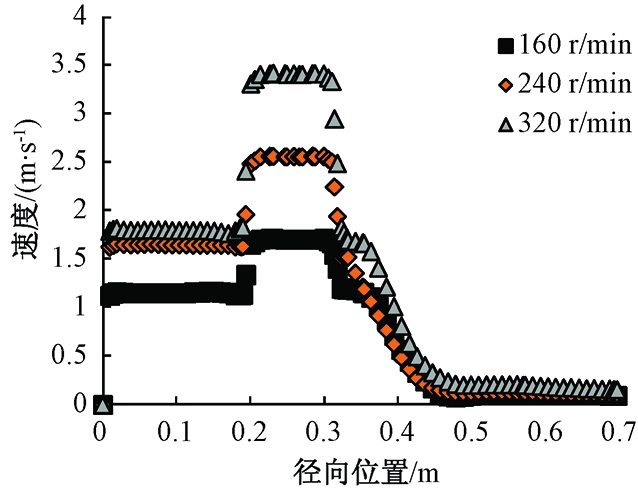
图9 不同转速下轴向速度分布曲线
Fig.9 Diagram of axial velocity distribution under different stirring speeds
分析图8可知,直线A上的速度为对称分布,速度从搅拌罐壁到叶端不断增大,在叶端处达到最大值.随着转速增加,流场速度在径向上逐渐增加,但增加的趋势略有减缓.分析图9可知,从罐底部到叶端处,速度保持在一定水平,当达到叶端处,速度达到最大值,其最大值范围与叶片的高度相关.在越过叶端后,速度逐渐递减.随着转速增加,流场速度在轴向上逐渐增加,但增加的趋势略有减缓.综上分析,随着转速增加,流场的速度逐渐增加,但是仅叶端的最大速度增加较为明显.因此,在满足搅拌效果的情况下,选择适宜的转速可以节约能耗.
2.4 浸入深度对流速场的影响
在图3上选取XOZ截面上直线B和直线C作为衡量不同浸入深度下流场径向和轴向速度分布的参照,直线B位于1/2液深.图10和图11分别为转速为240 r/min,搅拌器浸入深度分别为214、276、338 mm的直线B上径向速度和轴向速度分布曲线.
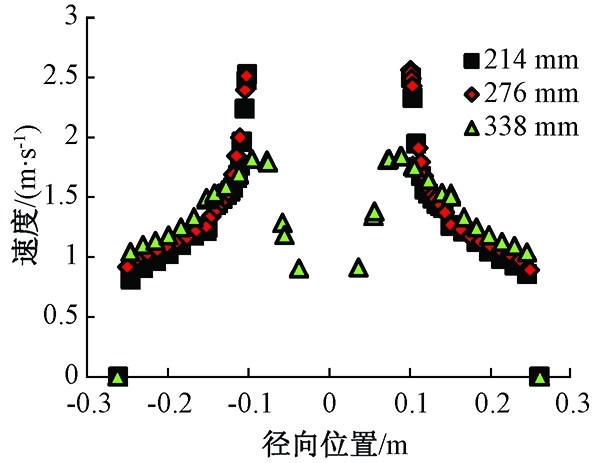
图10 不同浸入深度下的径向速度分布曲线
Fig.10 Diagram of radial velocity distribution under different stirrer immersed depths
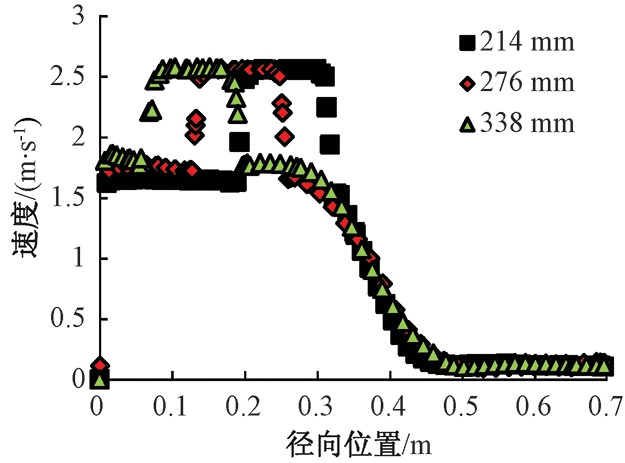
图11 不同浸入深度下的轴向速度分布曲线
Fig.11 Diagram of axial velocity distribution under different stirrer immersed depths
图10中对应搅拌器浸入深度为214 mm和276 mm的径向速度分布与图8中的径向速度分布相似,这是由于在该液深下直线B位于叶片高度范围内.而当搅拌器浸入深度为338 mm时,搅拌器完全浸没到直线B以下,速度从搅拌罐侧壁到搅拌器叶端处逐渐增加,在达到最大值之后沿搅拌轴方向逐渐减小.随着浸入深度的增加,同一液深下的最大速度逐渐减小,搅拌罐侧壁附近的速度在径向上略有增加.分析图11可知,搅拌罐内流场的最大速度分布在搅拌器叶端,随着搅拌器浸入深度的增加,最大速度逐渐靠近搅拌罐底部.搅拌罐底部附近的速度在轴向上略有增加,而叶轮上方的速度在轴向上略有降低.因此,随着搅拌器浸入深度的增加,流场的最大速度逐渐靠近搅拌罐底部.搅拌罐侧壁和底部附近的速度逐渐增加,有利于脱硫剂颗粒与搅拌罐底部流场的混合,而远离搅拌器上方附近的速度逐渐减小,削弱了脱硫剂颗粒与搅拌罐上部流场的混合.
2.5 转速对自由液面的影响
KR法脱硫搅拌过程中形成的漩涡卷吸脱硫剂颗粒进入铁水内部,从而与铁水充分混合并发生脱硫反应以实现脱硫目的.自由液面漩涡的形态将直接影响脱硫剂颗粒的分散过程,从而影响脱硫反应的最终效果.图12为搅拌器浸入深度为338 mm时不同转速下的自由液面波形图.由图12可以看出,机械搅拌过程中自由液面的漩涡深度和漩涡高度均随转速的增加而不断增大,自由液面的漩涡底部随着转速增加逐渐延伸到搅拌器叶轮上部,最终到达搅拌器底部.整个自由液面呈V字型的抛物状,并随转速增加在径向上不断扩大.搅拌器转速增加促使漩涡底部延伸至搅拌罐底部,虽然有助于脱硫剂分散,但是也会将整个搅拌器叶轮暴露在空气中,降低搅拌效果.
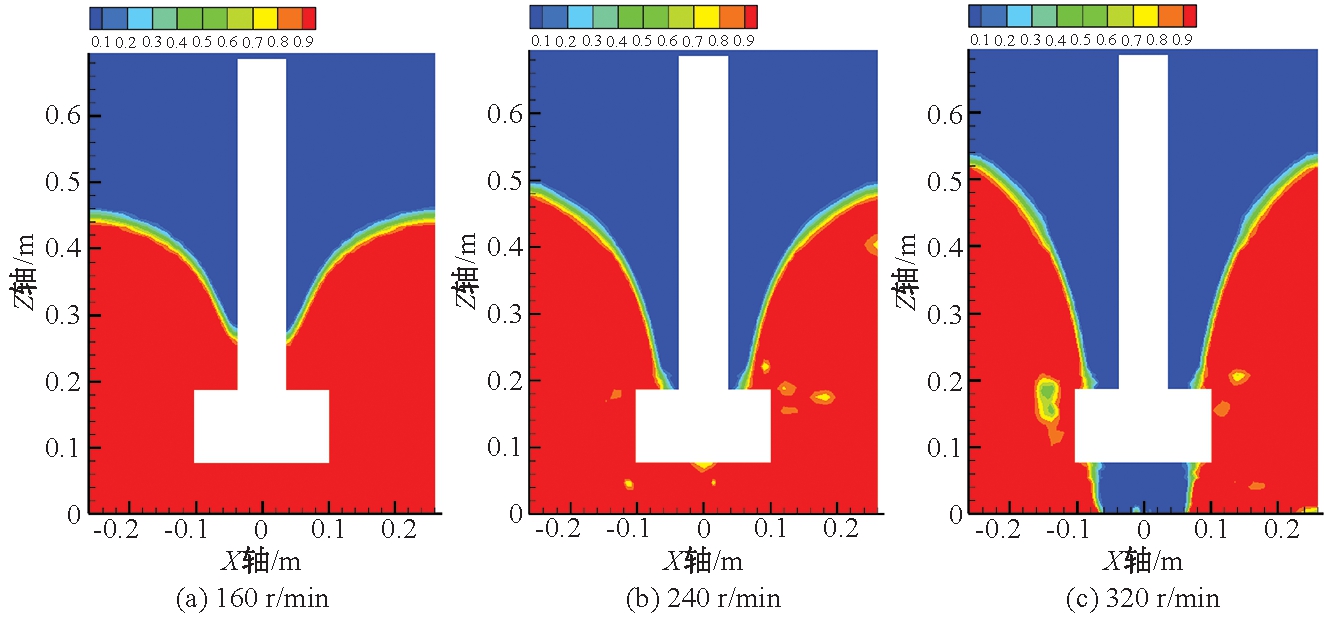
图12 各转速下的自由液面波形图
Fig.12 Surface fluctuation under different stirring speeds
2.6 脱硫剂颗粒分散的空间分布规律
采用DPM方法将脱硫剂固体颗粒离散为球状粒子单元,与流体连续相单元进行耦合建模,可得到脱硫剂颗粒在搅拌罐内的运动轨迹和空间离散分布等利用传统多相流模型无法得到的仿真内容.在转速为160 r/min工况下,搅拌开始时,颗粒从搅拌罐顶部自由下落,其运动轨迹如图13所示.从图13可以看出,2 s时刻的液面开始略微呈现下凹的漩涡,此时的脱硫剂颗粒速度较小,在浮力作用下漂浮于液面,并逐渐向搅拌轴靠拢;在4 s时刻,自由液面形成明显的漩涡,脱硫剂受到漩涡的卷吸作用聚集在搅拌轴附近的强漩涡中心处,并随着漩涡深度的增加而逐渐向下运动;在10 s之前,脱硫剂颗粒主要分布在强制涡流区,无法扩散到流场内部,此时的混合的效果较差;在10 s以后,自由液面的漩涡底部延伸至搅拌器叶轮上部,脱硫剂获得较大的速度,并通过与搅拌器的碰撞作用而克服流体阻力进入流场内部,通过4股循环流动实现与铁水的充分混合.将图12(a)与图13(c)对比分析可知,在相同的转速下,搅拌器浸入深度较浅时能促进漩涡底部延伸至搅拌器叶轮上部;而在同一浸入深度下,转速直接决定漩涡底部延伸至叶轮上部的能力.由于搅拌器转速和浸入深度直接决定漩涡底部延伸至搅拌器叶轮的能力,从而影响脱硫剂颗粒与铁水混合反应的效果.
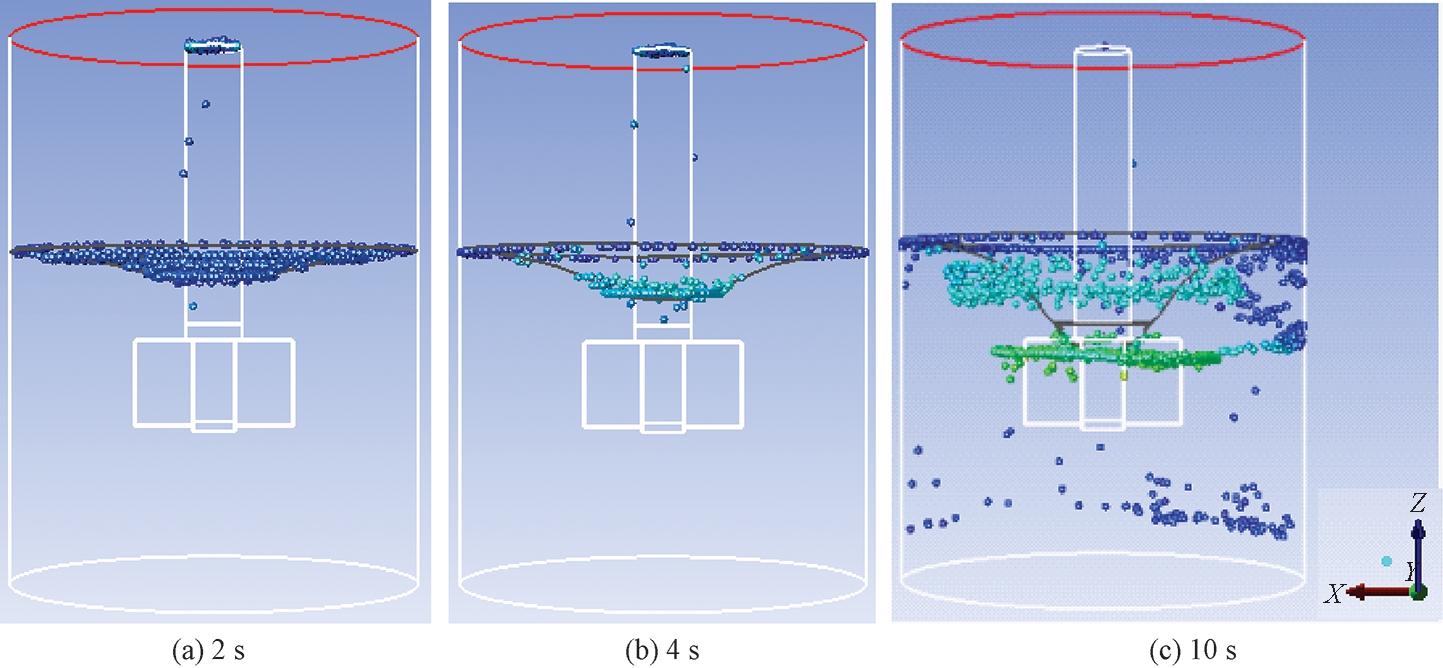
图13 不同时刻脱硫剂分散的空间分布
Fig.13 Spatial distribution of desulfurizer dispersion at different times
3 结论
笔者探究了搅拌器转速和浸入深度对流场速度分布、自由液面漩涡和脱硫剂分散的影响规律.数值模拟与水模试验得到的自由液面漩涡深度及高度结果一致,验证了数值模拟的可行性.数值模拟主要得到以下结论:
(1) 在固定转速下,搅拌罐内流场的最大速度位于搅拌器叶端,流场内部存在4股影响脱硫剂颗粒混合的循环流动.随着搅拌器转速的增加,搅拌罐内流场的速度在径向和轴向上逐渐增加.
(2) 随着搅拌罐浸入深度的增加,流场的最大速度逐渐靠近搅拌罐底部,搅拌罐侧壁和底部附近的速度逐渐增加,有利于脱硫剂颗粒与搅拌罐底部流场的混合,而远离搅拌器上方附近的速度逐渐减小,削弱了脱硫剂颗粒与搅拌罐上部流场的混合.
(3) 自由液面的漩涡底部随着转速增加逐渐延伸到搅拌器叶轮上部,最终到达搅拌器底部.整个自由液面呈V字型的抛物状,并随转速增加在径向上不断扩大.
(4)通过DPM方法得到大量脱硫剂颗粒在搅拌罐内的空间分布状况,搅拌器转速和浸入深度直接决定漩涡底部延伸至搅拌器叶轮的能力,当漩涡底部到达叶轮顶部时,脱硫剂颗粒将与叶轮直接接触而获得较大速度,使其克服流体的浮力和阻力进入流体内部,增强其与内部铁水的混合及反应作用.
参考文献:
[1] 李志杰, 张召, 杨小光, 等.KR法脱硫搅拌转速对流场影响的数值分析[J]. 山东冶金, 2016, 38(1): 27-30.
[2] 程新德, 孙江龙, 周家健, 等.KR法铁水脱硫的流动数值模拟分析[J]. 武汉科技大学学报 (自然科学版), 2015,38(5): 330-335.
[3] 欧阳德刚, 朱善合, 李明晖, 等. KR 搅拌脱硫传输动力学水模实验研究及进展[J]. 钢铁研究,2011, 39(5): 49-53.
[4] NAKAI Y, HINO Y, SUMI I, et al. Effect of flux addition method on hot metal desulfurization by mechanical stirring process[J]. Tetsu-to-hagane, 2015, 101(1):1-10.
[5] XU A J, ZHANG M L, ZHANG H N,et al. Simulation of thermo dynamics and kinetics for KR desulphur-ization[J]. ISIJ international, 2011, 18(S2): 98-106.
[6] NAKAI Y, SUMI I, MATSUNO H, et al. Effect of flux dispersion behavior on desulfurization of hot metal[J]. ISIJ international, 2010, 50(3): 403-410.
[7] NAKAI Y, SUMI I, KIKUCHI N,et al. Aggregation behavior of desulfurization flux in hot metal desulfurization with mechanical stirring[J]. ISIJ international, 2013, 53(8): 1411-1419.
[8] BUSCIGLIO A, CAPUTO G, SCARGIALI F. Free-surface shape in unbaffled stirred vessels: experimental study via digital image analysis[J]. Chemical engineering science, 2013, 104:868-880.
[9] BRUCATO A, CIPOLLINA A, MICALE G, et al. Particle suspension in top-covered unbaffled tanks[J]. Chemical engineering science, 2010, 65(10): 3001-3008.
[10] 党林贵, 郭淑雪, 王定标, 等. 不同组合桨搅拌器搅拌特性的数值研究[J]. 郑州大学学报(工学版), 2013,34(3): 59-63.
[11] YEOH S L, PAPADAKIS G, YIANNESKIS M. Numerical simulation of turbulent flow characteristics in a stirred vessel using the LES and RANS approaches with the sliding/deforming mesh methodology[J]. Chemical engineering research and design, 2004, 82(7): 834-848.
[12] 奚超超, 文光华, 刘江, 等. KR 铁水脱硫罐内流场优化模拟[J]. 炼钢, 2016, 32(1): 1-5.
[13] 王永庆, 朱冰, 赵頔,等. 一种强化换热流道的传热特性及流体扩散性分析[J]. 郑州大学学报(工学版), 2017,38(1):41-45.
[14] 李良超, 杨军, 徐斌. 轻密度颗粒在搅拌槽内悬浮特性的数值模拟[J]. 农业工程学报, 2013, 29(16): 42-49.