0 引言
由于工程材料(尤其是岩土材料)的特殊性(非均匀、有缺陷和不确定性),对工程材料的本构模型研究具有相当的复杂性和艰巨性.因此弹性、塑性、热塑性、热黏塑性、连续介质损伤理论等常被用以建立工程材料的本构模型.美国学者Desai等[1-3]提出了扰动状态概念(disturbed state concept)本构模型(DSC本构模型),假定材料在作用力下从最初的相对完整状态经过一个自调整和自组织过程达到最终的完全调整状态,分别用不同的本构关系描述两种不同状态的材料,建立扰动函数来描述材料从相对完整状态到完全调整状态的变化过程.Katti等[4]将扰动状态概念用于黏性土本构模型.Shao等[5]编制了嵌有DSC模型的动力有限元程序DYN2D,并将该程序用于模拟桩基施加循环荷载的现场试验.Park等[6]将DSC模型用于砂土在循环荷载作用下的液化分析.Desai等[7]基于扰动状态概念对饱和孔隙材料进行分析.MINH等[8]基于DSC模型模拟了砂土的软化特性.在扰动状态本构模型用于软黏土方面,付平等[9]基于扰动状态概念以Duncan-Chang 模型描述相对完整状态下材料的响应,以临界状态模型描述完全调整状态下颗粒材料的力学行为.于小军等[10]运用电阻率不规则因子表征和测定土样的扰动变量,建立了一个考虑结构性的软黏土本构模型.刘维正等[11]将附加孔隙比用来作为表征原状土的结构状态参数,基于扰动状态概念得到一维扰动状态概念压缩模型.刑国起等[12]研究了适用于描述结构性强度和变形规律的新型结构三维本构模型.经过Desai不断研究,该理论已经推广和应用到多种工程材料,如:饱和土(砂土和黏土)、非饱和土、岩石和堆石料、混凝土、界面和节点、金属和合金、聚合物、陶瓷等[13].
然而,作为工程材料的统一模型,DSC本构模型并不是针对岩土材料提出的,而是从金属或其他无明显体积变形的工程材料提出的,模型中扰动函数只考虑塑性偏应变对扰动的影响而没有考虑塑性体积应变的影响.笔者改进Desai等人提出的DSC模型(以下简称DSC本构模型)的扰动函数,使之能够考虑塑性体积应变对扰动的影响.并通过室内固结不排水三轴试验、室内固结排水三轴试验和室内一维压缩试验验证了改进扰动函数的DSC本构模型的正确性和在模拟结构性软土上的优越性.
1 扰动状态本构理论
扰动状态本构理论认为:在变形的任何一个阶段,材料单元的一部分处于相对完整状态,另一部分达到完全调整状态或临界状态.材料是相对完整状态(RI)的部分和完全调整状态(FA)部分的随机的混合体.在材料的变形过程中,材料逐渐从初始相对完整状态达到完全调整状态.因此,材料的总体响应是相对完整状态和完全调整状态的耦合作用,可以通过相对完整状态的响应和完全调整状态的响应来表达.如图1所示,扰动状态概念通过一个扰动因子D来衡量处于相对完整状态的材料和处于完全调整状态的材料所占的权重.为扰动因子D建立一个与塑性应变相关的扰动函数来描述这种微结构变化的过程.扰动状态概念(DSC)通过扰动函数考虑相对完整状态和完全调整状态的耦合作用,不需要在微观结构上定义材料的响应.如图1所示,在初始相对完整状态下,D=0,随着塑性应变的发展,扰动状态的部分逐渐增多,D>0,最终达到完全调整状态D=1.
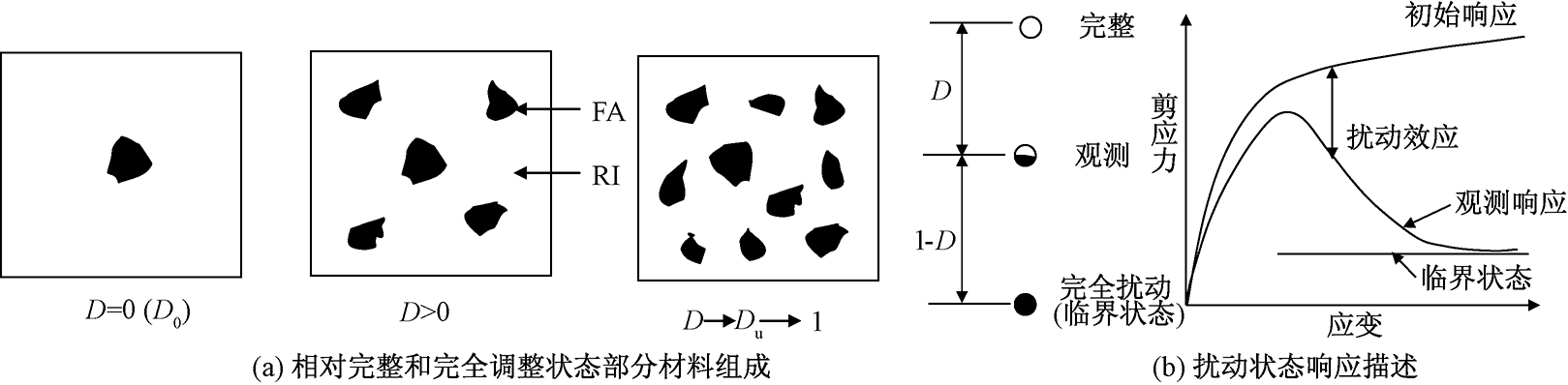
图1 扰动状态概念示意图
Fig.1 Schematic view of disturbed state concept
因此DSC本构模型的观测响应可以表示为:
dσa=(1-D)dσi+Ddσc+dD(σc-σi),
(1)
式中:a、i、c分别用来表示同观测响应、相对完整状态响应和完全调整响应;σ和ε分别表示应力和应变张量;D是标量型的扰动因子.DSC本构模型用分级单屈服面模型(HISS模型)[14]描述相对完整状态的响应.HISS模型是一个统一的塑性模型,有多种不同的版本用于描述关联的各向同性硬化、非关联的各向同性硬化、各向异性硬化和黏塑性等.笔者只采用其最基本的模型δ0版本.该模型的屈服面表达式为:
(2)
Fb=-α![]() n+γ
n+γ![]() 2;
2;
(3)
Fs=(1-βSr)-0.5;
(4)
(5)
式中:J1为应力张量的第一不变量;J2D和J3D分别为偏应力张量的第二和第三不变量;γ、β、n、3R为材料参数;α为硬化函数.该模型参数的物理含义及确定方法参考文献[13-14].
α=α(ξ,ξv,ξD),
(6)
式中:ξ、ξv、ξD分别为塑性总应变、塑性体积应变和塑性偏应变的迹.
完全扰动状态可以用临界状态模型来描述[13],临界状态下的响应可用以下公式来描述:
;
(7)
![]() ;
;
(8)
(9)
式中:ec为临界孔隙比;![]() 为
为![]() 时的临界孔隙比;
时的临界孔隙比;![]() 和
和![]() 分别临界状态下偏应力张量的第二不变量和应力张量的第一不变量;λ和
分别临界状态下偏应力张量的第二不变量和应力张量的第一不变量;λ和![]() 为模型参数,分别为e-lnP平面各向同性压缩曲线斜率和
为模型参数,分别为e-lnP平面各向同性压缩曲线斜率和![]() 平面临界状态线斜率.
平面临界状态线斜率.
2 扰动函数改进
扰动函数D发挥耦合作用,通过耦合RI和FA两种响应来确定观测响应.对于饱和土体,扰动因子可以通过下式确定:
(10)
式中:σ选用合适的应力,可以是轴应力σ1、剪应力τ、主应力差σ1-σ3或者![]() 上标i、c、u分别表示相对完整状态、临界状态和实际观测状态.
上标i、c、u分别表示相对完整状态、临界状态和实际观测状态.
DSC本构模型的扰动函数一般用下式来表达[12]:
(11)
式中:Du为极限扰动参数;A和Z为扰动函数的参数;ξD为塑性偏应变的迹.
DSC本构模型是从金属或其他变形过程中没有明显体积应变的材料出发提出的,模型中的扰动函数只考虑了塑性偏应变的影响.而对于土体,尤其是结构性软土这种材料,土体结构性的扰动不但会由塑性偏应变引起,而且会由塑性体积应变引起,这两种应变同时存在.在研究其结构性扰动的时候仅仅考虑其中任何一方面都是不全面的.因此,扰动变量采用这两种应变的耦合形式是一种较好的解决思路.如何耦合可以有很多方式,笔者提出在原扰动函数的基础上引入一个塑性偏应变迹和塑性体积应变迹的耦合形式作为扰动函数的扰动变量,如下式所示:
(12)
式中:ξV为塑性体积应变的迹;ξD为塑性偏应变的迹.分别可通过式(13)和(14)计算得到.
(13)
(14)
(15)
式中:![]() 分别为塑性体积应变和塑性偏应变张量;δ为耦合参数,这是比例参数,本身没有物理意义,仅用于表达塑性体积应变和塑性偏应变对扰动的贡献比例,当δ=0时,扰动完全由塑性体积应变产生,当δ=1时,扰动完全由塑性偏应变产生,扰动函数退化为原来的形式,实际上对于土体材料,0<δ<1.在进一步深入研究之前,具体δ的值可通过对试验应力应变曲线的拟合得到,为方便使用,在工程中令δ=0.5可满足精度要求.
分别为塑性体积应变和塑性偏应变张量;δ为耦合参数,这是比例参数,本身没有物理意义,仅用于表达塑性体积应变和塑性偏应变对扰动的贡献比例,当δ=0时,扰动完全由塑性体积应变产生,当δ=1时,扰动完全由塑性偏应变产生,扰动函数退化为原来的形式,实际上对于土体材料,0<δ<1.在进一步深入研究之前,具体δ的值可通过对试验应力应变曲线的拟合得到,为方便使用,在工程中令δ=0.5可满足精度要求.
根据新的扰动变量ξδ,则改进后的扰动函数如下式所示:
(16)
3 改进扰动函数后的模型验证
DSC本构模型一般采用δ0版本的各向同性HISS模型[14]描述相对完整(RI)状态,采用临界状态模型描述完全扰动(FA)状态,并采用相关联流动法则.笔者自编Fortran程序对室内试验(三轴压缩试验、一维压缩试验)进行模拟.其计算过程为首先利用HISS模型计算相对完整(RI)状态的应力,然后在假设![]() 基础上,计算完全调整状态的应力,从而利用扰动函数D计算DSC本构模型实际的应力.其编程步骤如下.
基础上,计算完全调整状态的应力,从而利用扰动函数D计算DSC本构模型实际的应力.其编程步骤如下.
(1)将硬化参数ξ、ξD、ξV作为状态变量,计算硬化参数ξ、ξD、ξV的初始值.
(2)计算弹性刚度矩阵Ce,用弹性刚度矩阵Ce计算试探应力dσ=Ce·dε.
(3)根据试探应力判断HISS模型屈服面F是否大于0.
(4)如果F<0,则此增量步为弹性加载或者弹性卸载,弹性试探应力即为增量步后的RI状态实际应力.
(5)如果F>0,则此增量步为弹塑性加载,判断此增量步开始前的屈服面是否F<0.
(6)如果增量步开始前屈服面F<0,说明增量步开始前的应力点处于弹性域内,在本增量步内产生屈服,用牛顿迭代法判断产生屈服时的应力![]() 计算产生屈服部分的应变增量.
计算产生屈服部分的应变增量.
(7)如果增量步开始前的屈服面F≥0,说明此增量步处于塑性状态,应变增量全部产生屈服.
(8)将产生屈服的应变增量分为N个子增量进行弹塑性计算,即![]()
(9)判断每一子增量步后是否![]() 如果是,计算弹塑性矩阵
如果是,计算弹塑性矩阵![]() 和新的硬化参数.并转回步骤(9)继续进行下一增量步计算;如果不是,则进行漂移修正,然后计算弹塑性矩阵
和新的硬化参数.并转回步骤(9)继续进行下一增量步计算;如果不是,则进行漂移修正,然后计算弹塑性矩阵![]() 和新的硬化参数,转回步骤(9)继续进行下一增量步计算.
和新的硬化参数,转回步骤(9)继续进行下一增量步计算.
(10)循环进行步骤(9)和(10),直到完成N个子增量步计算,得到增量步后RI状态的实际应力σi、弹塑性刚度矩阵和硬化参数.
(11)假设![]() 根据临界状态模型计算完全扰动状态的应力
根据临界状态模型计算完全扰动状态的应力![]()
(12)根据增量步中产生的塑性应变计算扰动函数D.
(13)计算DSC本构模型的实际应力σa=(1-D)σi+Dσc.
HISS模型的独立参数包括弹性模量E、泊松比v、极限参数γ、形状参数β、相变参数n;临界状态参数包括各向同性压缩曲线斜率λ、临界状态线斜率![]() 和初始临界孔隙比
和初始临界孔隙比![]() ;扰动参数包括极限扰动参数Du和扰动参数A和Z.各参数的物理意义及其确定方法详见文献[13],可采用Desai编制的Parameters-Back Prediction程序计算DSC本构模型的参数,只需要将3组不同围压下的室内3轴试验(CU试验或CD试验)应力应变数据导入程序即可自动计算出以上各个参数.
;扰动参数包括极限扰动参数Du和扰动参数A和Z.各参数的物理意义及其确定方法详见文献[13],可采用Desai编制的Parameters-Back Prediction程序计算DSC本构模型的参数,只需要将3组不同围压下的室内3轴试验(CU试验或CD试验)应力应变数据导入程序即可自动计算出以上各个参数.
通过一种室内试验获取本构模型参数,然后再通过其他没有用来获取模型参数的室内试验或现场试验进行验证才能更好地验证本构模型.为验证改进后的本构模型,取温州结构性软土做了一系列3轴压缩试验和一维压缩试验.取土位置位于温州民营科技产业基地滨海园区,取土深度为地面以下2 m,通过薄壁取土器取得原状结构性软土.笔者通过3轴固结不排水(CU)试验应力应变数据导入Parameters-Back Prediction程序获取模型参数,并通过3轴固结排水(CD)剪切试验和一维压缩试验应力应变数据对改进后的模型进行验证.
通过3轴固结不排水(CU)试验获得的DSC本构模型参数如表1所示.
表1 温州结构性软土DSC本构模型参数
Tab.1 DSC constitutive model parameters of Wenzhou structured clay

E/MPavγβnh1h2ec0λmDuAZ1.790.350.00260.582.30.001260.421.320.130.0750.991.690.31
对于改进扰动函数后的DSC本构模型,通过3轴固结不排水(CU)试验确定改进后的扰动函数的参数A=1.88,Z=0.33,δ=0.5(δ=0.5为默认值),其他参数均与改进前相同,如表1所示.用DSC本构模型和改进后DSC模型分别模拟温州结构性软土3轴固结不排水(CU)试验、三轴固结排水(CD)试验和一维压缩试验,将模拟结果与试验数据进行比较.
DSC本构模型和改进后的DSC本构模型对CU试验的模拟结果如图2所示,对CD试验的模拟结果如图3所示,对一维压缩试验的模拟结果如图4所示.
通过图2和图3中DSC本构模型和本文改进后的DSC本构模型模拟3轴CU和CD试验结果的比较可以看出,改进后的DSC本构模型对3轴试验应力应变关系的模拟结果与试验结果更为吻合,DSC本构模型预测的强度偏高,改进后DSC本构模型对这一缺点有所改进,在三轴CD试验中这一点尤其明显.图4可以看到,由于没有考虑塑性体积应变对结构的破坏(扰动),DSC本构模型模拟一维压缩试验得到的结构屈服压力比实际偏大,对扰动函数改进后能够更好地预测一维压缩过程中由于结构的破坏而发生的孔隙比的减小.
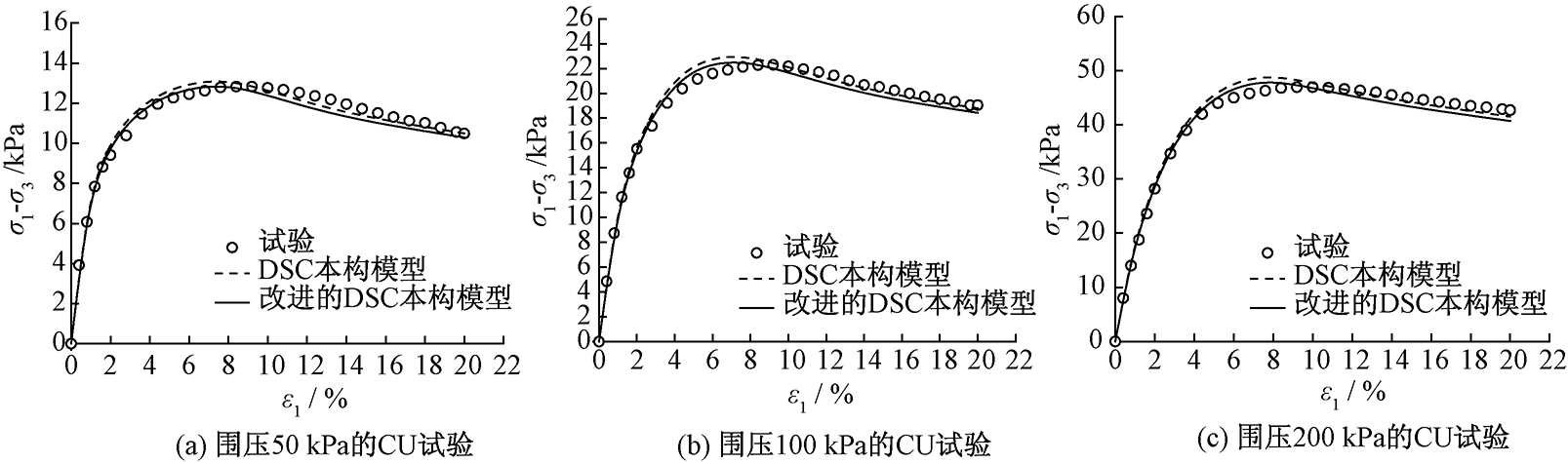
图2 DSC本构模型和改进的DSC本构模型模拟3轴固结不排水(CU)试验结果对比
Fig.2 Comparison of DSC constitutive model and modified DSC constitutive model via simulation of CU test
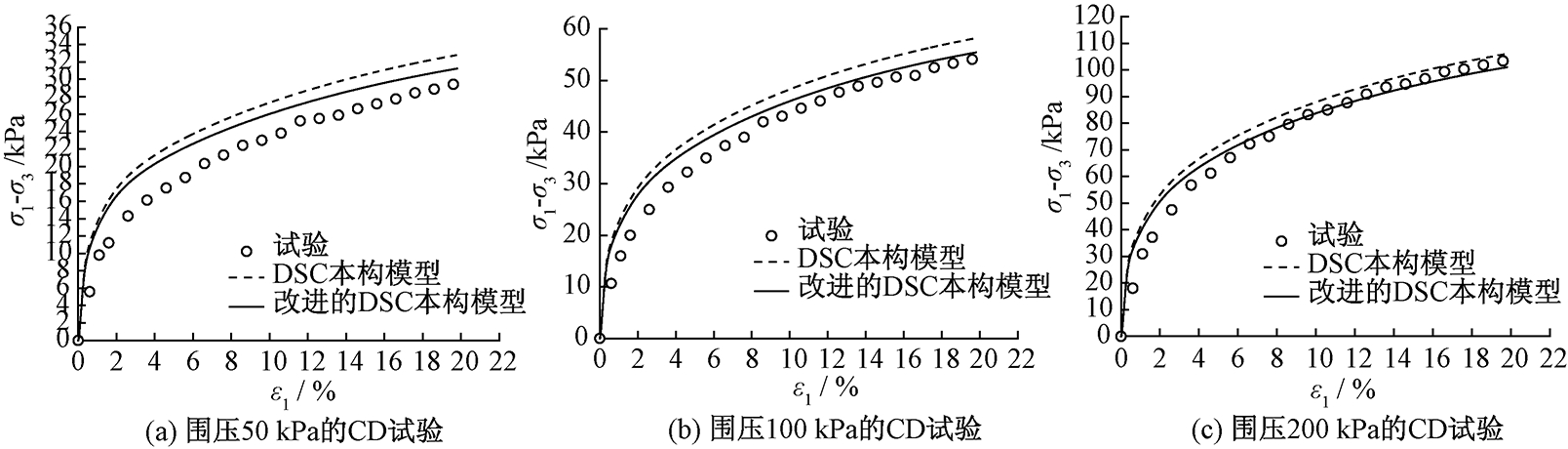
图3 DSC本构模型和改进的DSC本构模型模拟3轴固结排水(CD)试验结果对比
Fig.3 Comparison of Desai’s DSC constitutive model and modified DSC constitutive model via simulation of CD test
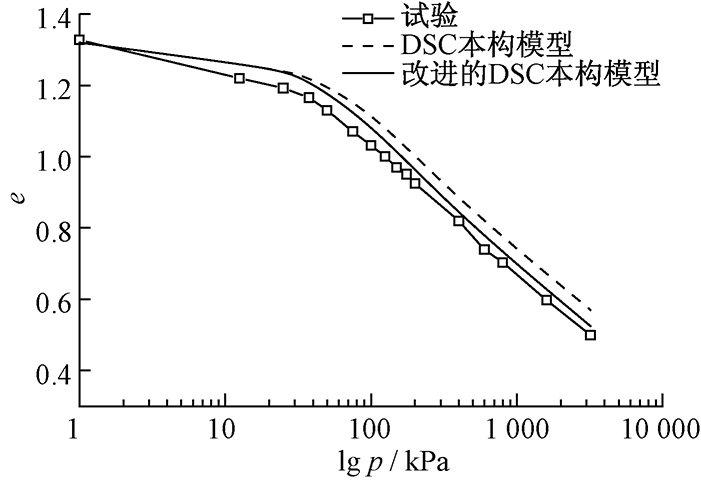
图4 DSC本构模型和改进的DSC本构模型模拟一维压缩试验结果对比
Fig.4 Comparison of DSC constitutive model and modified DSC constitutive model via simulation of one dimensional compression test
值得说明的是,图2为CU试验结果,是笔者用于确定模型参数的,由于部分扰动参数是通过拟合应力应变曲线得到的,因此改进前后的模拟结果与试验数据相比均很接近,这是正常的.图3和图4是CD试验和一维压缩试验模拟结果与试验数据的对比,用于验证模型精确性,从对比结果来看还是能够明显看到改进后的模型模拟结果与试验数据更为吻合,从图上来看差异没有想象的那么显著,这是由于原状结构性软黏土的室内试验有难度,原状土在取回和试验的过程中本身扰动就已经发生,很难做到完全的原状样.虽然无法保证对完全原状土做试验,但结构性特征都已经明显表现出来,而且改进前后对比的差异也能够被证明.从图3(c)中看到围压200 kPa下模型在改进前后的模拟结果相差不大,这是由于在较大的围压下土体的应变以塑性体积应变为主,本模型在改进前以塑性体积应变为扰动变量,能够反映塑性体积应变对结构性扰动的影响.改进后的模型参数虽然考虑了塑性体积应变与塑性偏应变的共同影响,但所采用的耦合参数是一个固定的比例参数,不受应力水平的影响,如果能够在耦合参数中考虑应力水平的影响,将对本文模型是个比较大的提升,也是作者要进一步努力的方向.因为对道路、涵洞等自重压力不高的软土地基静力特性和动力特性方面的研究[15-16]均表明,地基的承载特性主要由浅层土体决定,如地下20 m以上,软土地基的结构性特征也在浅层土体中表现最为明显.常规(较低)应力水平下对土体结构性扰动模拟准确与否对工程计算的准确性具有重要意义.笔者改进后的模型对于浅层土体应力应变性质的模拟更具有优势,而在深层土体(较高应力水平),笔者改进后的模型也能够满足工程计算精确性的要求.
原状结构性软土受力后发生的塑性体积应变是非常明显的,塑性体积应变的扩展也会破坏土体的结构,从而使土体由相对完整状态向完全调整状态转变.DSC本构模型的扰动函数只考虑了塑性偏应变对扰动的影响,而没有考虑塑性体积应变的影响,因而DSC本构模型对结构性软土这种受力后会产生较大体积应变的材料的模拟有一定的误差,改进后的DSC本构模型增加了塑性体积应变对扰动的影响,因而更加符合土体的力学特性,对结构性软土应力应变关系的描述也更精确一些.改进后DSC本构模型这一特点对除原状结构性软土外的其他岩土材料的适用性需要进一步的试验验证.
4 结论
(1)DSC本构模型作为工程材料的统一模型,只考虑塑性偏应变对扰动状态的影响,而没有考虑塑性体积应变对扰动状态的影响.岩土材料塑性体积应变对扰动状态的影响相当显著,应在岩土本构模型中予以考虑.
(2)对DSC本构模型的扰动函数进行改进,在原扰动函数的基础上引入塑性偏应变迹和塑性体积应变迹的耦合形式作为扰动函数的扰动变量,能方便考虑塑性体积应变对岩土扰动状态的影响.
(3)通过温州结构性软土3轴固结不排水(CU)试验、3轴固结排水(CD)剪切试验和一维压缩试验应力-应变数据对改进后的模型进行验证.验证结果表明改进前模型对结构性软土的不排水强度和排水强度预测均略偏高,改进后的模型对结构性软土应力应变关系的模拟结果更为精确.
(4)改进扰动函数后增加了一个耦合参数δ,该参数的取值可通过对试验应力应变曲线的拟合得到,在工程中令δ=0.5可满足精度要求.
参考文献:
[1] DESAI C S. Disturbed state concept as unified constitutive modeling approach[J]. Journal of rock mechanics and geotechnical engineering, 2016, 8(3):277-293.
[2] DESAI C S, TOTH J. Disturbed state constitutive modeling based on stress-strain and nondestructive behavior[J]. International journal of solids and structures, 1996, 33(11): 1619-1650.
[3] DESAI C S. Constitutive modeling of materials and contacts using the disturbed state concept: part 1 - background and analysis[J].Computers & structures, 2015,146:234-251.
[4] KATTI R D, DESAI C S. Modeling and testing of cohesive soil using disturbed state concept[J]. Journal of engineering mechanics, 1995, 121 (5):648-658.
[5] SHAO C, DESAI C S. Implementation of DSC model and application of analysis of field pile load tests under cyclic loading[J]. International journal of numerrical and analytical methods in geomechanics, 2000, 44(6): 601-624.
[6] PARK I J, DESAI C S. Cyclic behavior and liquefaction of sand using disturbed state concept[J]. Journal of geotechnical and geoenvironmental engineering, 2000, 126(9): 834-846.
[7] DESAI C S, WANG Z. Disturbed state model for porous saturated materials[J]. International journal of geomechanics, 2003, 3(2): 260-265.
[8] MINH N H, SUZUKI K, ODA M, et al. Numerical simulation using disturbed state concept (DSC) model for softening behavior of sand[J]. Journal of southeast Asian geotechnical society, 2008, 34(1): 25-35.
[9] 付平, 楚锡华, 余村,等. 基于扰动状态概念的颗粒材料应变局部化行为模拟[J].华南理工大学学报(自然科学版), 2014, 42(4):59-69,71.
[10] 于小军, 齐志宏. 基于扰动状态概念的结构性软黏土本构模型[J]. 岩土工程学报, 2009, 31(12): 1882-1887.
[11] 刘维正, 石名磊, 缪林昌. 基于扰动状态概念的结构性土压缩特性分析[J]. 岩土力学, 2010, 31(11): 3475-3480.
[12] 邢国起,肖洪天,李大勇.一种新型结构性土三维本构模型[J].水利水电技术,2017,48(6):54-59.
[13] DESAI C S. Mechanics of materials and interfaces: the disturbed state concept[M]. CRC Press: Boca Raton, FL, 2001.
[14] DESAI C S, SOMASUNDARAM S, FRANTZISKONIS G. A hierarchical approach for constitutive modelling of geologic materials[J]. International journal for numerical and analytical methods in geomechanics, 1986, 10(3): 225-257.
[15] 张浩,杨玲,郭院成.交通荷载作用下低填道路软土地基的动力响应分析[J].郑州大学学报(工学版),2017,38(1):11-15.
[16] 马强,朱健,邢文文,等.软土硬壳层涵洞地基极限承载力分析[J].郑州大学学报(工学版),2016,37(1):70-74.