0 引言
连续刚构桥以其经济良好性和施工方便性在山区高速公路大跨度桥梁中得到快速的发展[1-2].连续刚构桥随着跨径的增长,桥墩的高度也在逐渐增高,目前大部分高墩是采用空心单薄壁墩,在承台和空心墩中间部分是采用实心过渡墩,《云南省高速公路连续刚构桥梁关键技术指南》规定空心薄壁墩墩底宜有适当的实心段以便承台和薄壁墩刚度过渡,建议墩底实心段取3~5 m,但是目前国内外尚鲜见文献对实心段的设计长度选取进行研究.国内外对桥墩及承台的刚度分析已经开展了较为系统的研究[3-8],文献[3]分析了承台刚度的影响因素,并对影响程度进行了研究;文献[4]分析了桩基础对于柔性墩墩顶抗推刚度的影响,推导出来墩顶抗推刚度;文献[5]通过连续刚构桥墩身变形机理分析,提出了主动变形阶段和被动变形阶段单肢墩的抗推刚度计算方法;文献[6]对高薄壁墩墩底弹性和墩底固结时的抗推刚度进行了分析,得出当墩高稍低或地基较柔时,计算桥墩抗推刚度必须计入弹性地基的影响;文献[7]以弹性支承的连续梁理论为基础,建立了任意荷载作用位置和任意布桩形式下承台刚度的计算方法;文献[8]通过将桩-承台体系简化为弹簧支承的连续梁,对承台的刚度进行了分析.目前工程中墩底实心段计算长度的选取都是依据设计经验来选取的,文献[4-9]只是对桥墩和承台的刚度进行了研究,并未对墩底实心段的刚度过渡进行分析,因此笔者将基于上述文献的分析,通过推导空心单薄壁墩空心段和实心段的顺桥向抗推刚度来对实心段过渡长度进行分析,并以工程实例验证了文章分析思路和推导过程的正确性和适用性.
1 桥墩抗推刚度计算
1.1 实心段墩身抗推刚度
连续刚构桥空心单薄壁墩在墩底与承台相接处一般都会采用实心段进行过渡,假设实心墩墩高为h1,空心段墩高为h2,空心薄壁墩实心段受到墩底承台的约束作用,墩底边界条件可以模拟成固结模式;墩顶受到墩高为h2的空心段的约束,可将空心段的自重转化为作用在墩顶的竖向荷载P1=A2h2ρ2,其中A2为空心段墩横截面面积,ρ2为空心墩材料容重.实心段墩身荷载集度为q1=A1ρ1,实心段抗推刚度计算模式如图1所示.
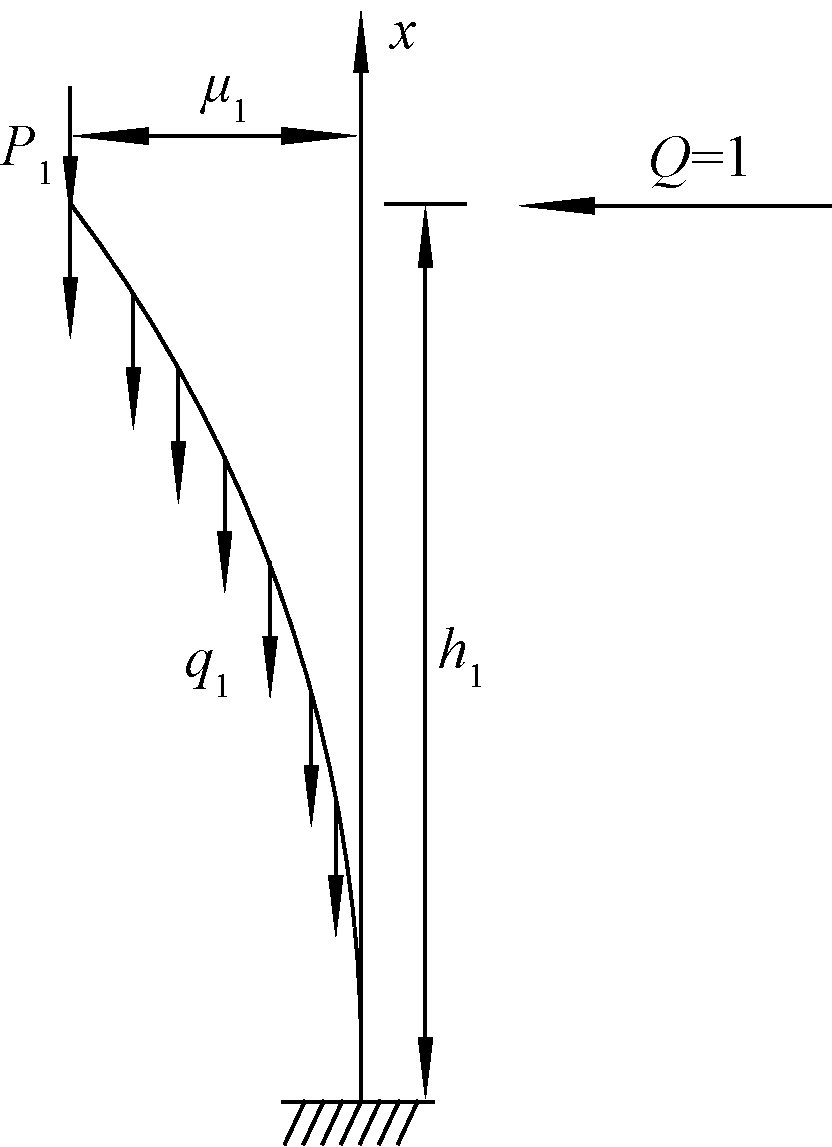
图1 实心段抗推刚度计算模式示意图
Fig.1 Calculation model schematic diagram of solid sections′ anti-pushing rigidity
假设墩身的近似变形曲线为:
(1)
总势能Π1为:
q1![]() Δ(x)dx-Qμ1,
Δ(x)dx-Qμ1,
(2)
式中,Δmax为弯曲变形后墩顶的最大竖向位移;Δ(x)是以Δmax为幅值按二次抛物线变化的竖向位移函数;E1为实心段墩身弹性模量;I1为实心段墩身截面惯性矩.
将公式(1)代入总势能公式(2),再由最小势能原理![]() 解得:
解得:
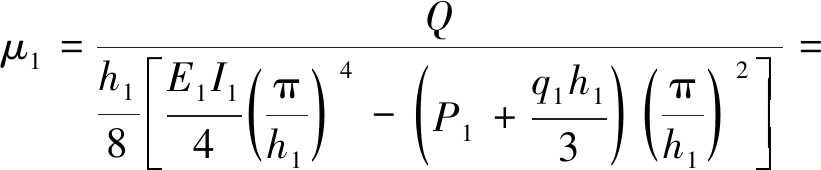
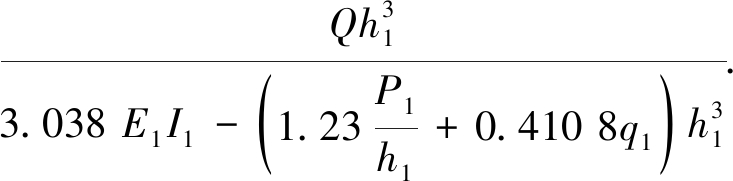
令Q=1,即可得实心段墩身的顺桥向抗推刚度:
(3)
1.2 空心段墩身抗推刚度
空心段的墩底和实心段的上部相连接,在连接部位两者有相同的水平位移和转角位移.分析空心段墩身抗推刚度时,可以将连接处的约束作用用弹簧约束刚度来表示,如图2所示,其中KH表示平动约束弹簧;KM表示转动约束弹簧;KHM表示平转动耦合约束弹簧[10-11].
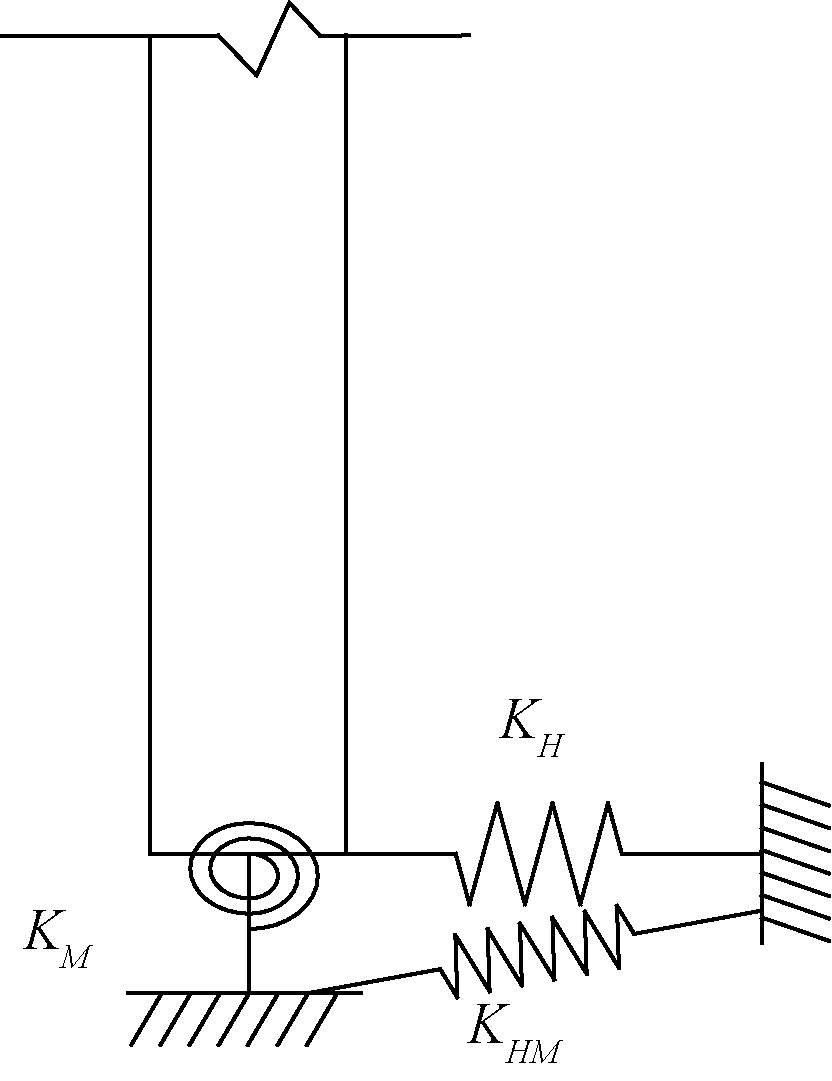
图2 连接处约束作用示意图
Fig.2 Schematic diagram of the constraint effect at the junction
假设在图2计算模式下,当空心段顶部作用单位水平力H=1,弯矩M=0时,在空心段墩底产生的转角为δMH,水平位移为δH;当空心段顶部作用单位弯矩M=1,水平力H=0时,在空心段墩底产生的转角为δM,水平位移为δHM,则可得此模式下约束的柔度系数矩阵,即
![]() 其中,δHM=δMH.
其中,δHM=δMH.
求柔度系数矩阵的逆矩阵,可得刚度系数矩阵:
高度为h2的空心段桥墩所承受的荷载主要有墩身自重q2,桥面及挂篮自重及挂篮施工时悬臂端不平衡竖向力和弯矩,将其简化为施加于桥墩墩顶形心处竖向集中力P2和水平推力F,如图3所示.
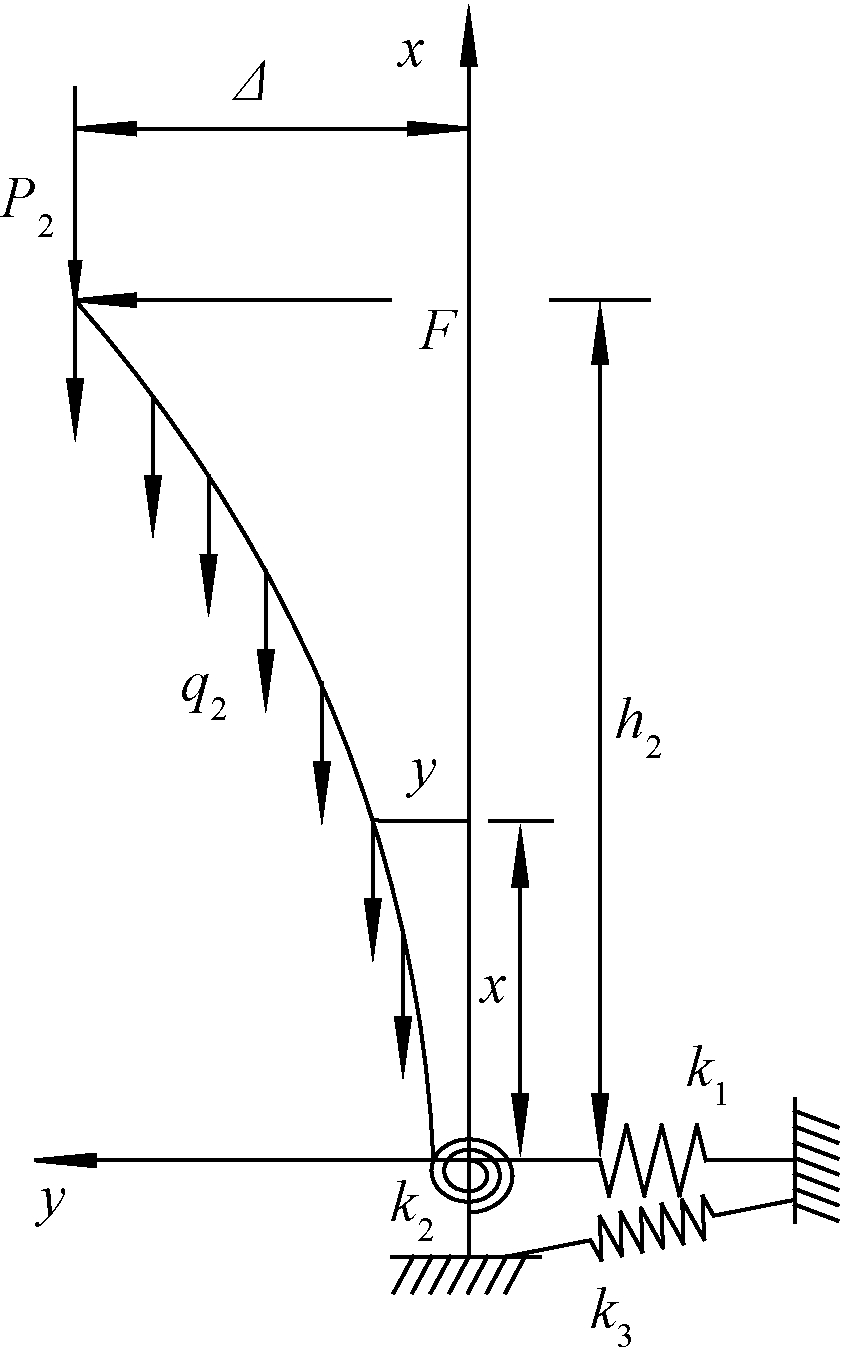
图3 空心段抗推刚度计算模式示意图
Fig.3 Calculation model schematic diagram of hollow sections′ anti-pushing rigidity
假设墩身变形函数为y2,则墩身自重引起的势能:
墩顶竖向集中力引起的势能为:
墩顶水平集中力引起的势能为:
V3=-Fy2(h2);
结构的应变能为:![]()
式中,E2为空心段墩身弹性模量;I2为空心段墩身截面惯性矩.
墩底的约束弹簧产生的弹簧势能为:
则墩的总势能为:
Π2=U1+U2+V1+V2+V3.
(4)
在弹簧KH、KM、KHM约束下,墩身将产生弹性弯曲变形、刚体转动和刚体平移三部分挠度.文献[11]指出墩身的形函数应取墩底固结时的弹性变形与由转动弹簧所产生的刚体转动位移及刚体平动位移之和.此处通过相应的等效,对墩本身的变形函数采用三次多项式表示,而刚体位移则用线函数表示,则墩身变形函数可取:
(5)
其中,y2i(i=1,2,3)分别表示墩顶在单位水平推力下,墩身弹性弯曲变形、刚体转动和刚体平移所引起的墩顶位移.
y23=δH+h2(-δMH).
当x=h2时,墩顶在单位水平推力下产生的位移y2(h2)=(y21+y22+y23)μ2[12].
将公式(5)代入总势能公式(4),得
F(y21+y22+y23)μ2.
由最小势能原理![]() 可得:
可得:
μ2=[F(y21+y22+y23)]/[(y21+y22+y23)-
![]() ].
].
墩顶在单位水平推力下产生的位移为:
y2(h2)=(y21+y22+y23)μ2,再令F=1,即可得空心段墩身的顺桥向抗推刚度:
k2=![]()
![]() ]/(y21+y22+y23)2.
]/(y21+y22+y23)2.
笔者在分析空心段墩身的顺桥向抗推刚度时,令P2=0,则
(6)
根据式(3)和式(6),将桥梁计算参数代入公式,使其在空心段和实心段交界处的抗推刚度基本保持相等,就可以计算出实心段墩身的高度h1.
2 算例分析
为验证本文关于空心段墩和实心段墩顺桥向抗推刚度计算公式和本文分析思路的正确性和适用性,下面以两个连续刚构桥梁为例,两个算例为沮河特大桥和柳沟大桥,桥墩类型均为单肢空心薄壁墩.通过式(3)和式(6)来计算实心过渡段的长度,并和工程实例进行对比,各桥计算参数如下.E1,2=3.25×104MPa,ρ1,2=25 kN/m3,算例1:A1=32.5 m2,A2=12.54 m2,h1=5 m,h2=52 m,I1=67.71 m4,I2=44.06 m4;算例2:A1=34 m2,A2=11.6 m2,h1=6 m,h2=72 m,I1=70.83 m4,I2=35.35 m4.
下面以算例1进行实心过渡段墩身长度的计算分析:将算例1的计算参数代入式(3),可得k1和h1的关系如图4实线所示.
由式(3)可知,当h1=0时,k1趋于无穷,可以认为墩底的抗推刚度为无穷大,本文分析时认为承台刚度也为无穷大,这样就可以认为承台和实心段墩底在连接处刚度实现了过渡.从图4可以看出随着h1的增大,k1在逐渐减小,减小幅度越来越小,根据算例1的实桥数据,当h1=5 m时,k1=4.91×104kN/m.
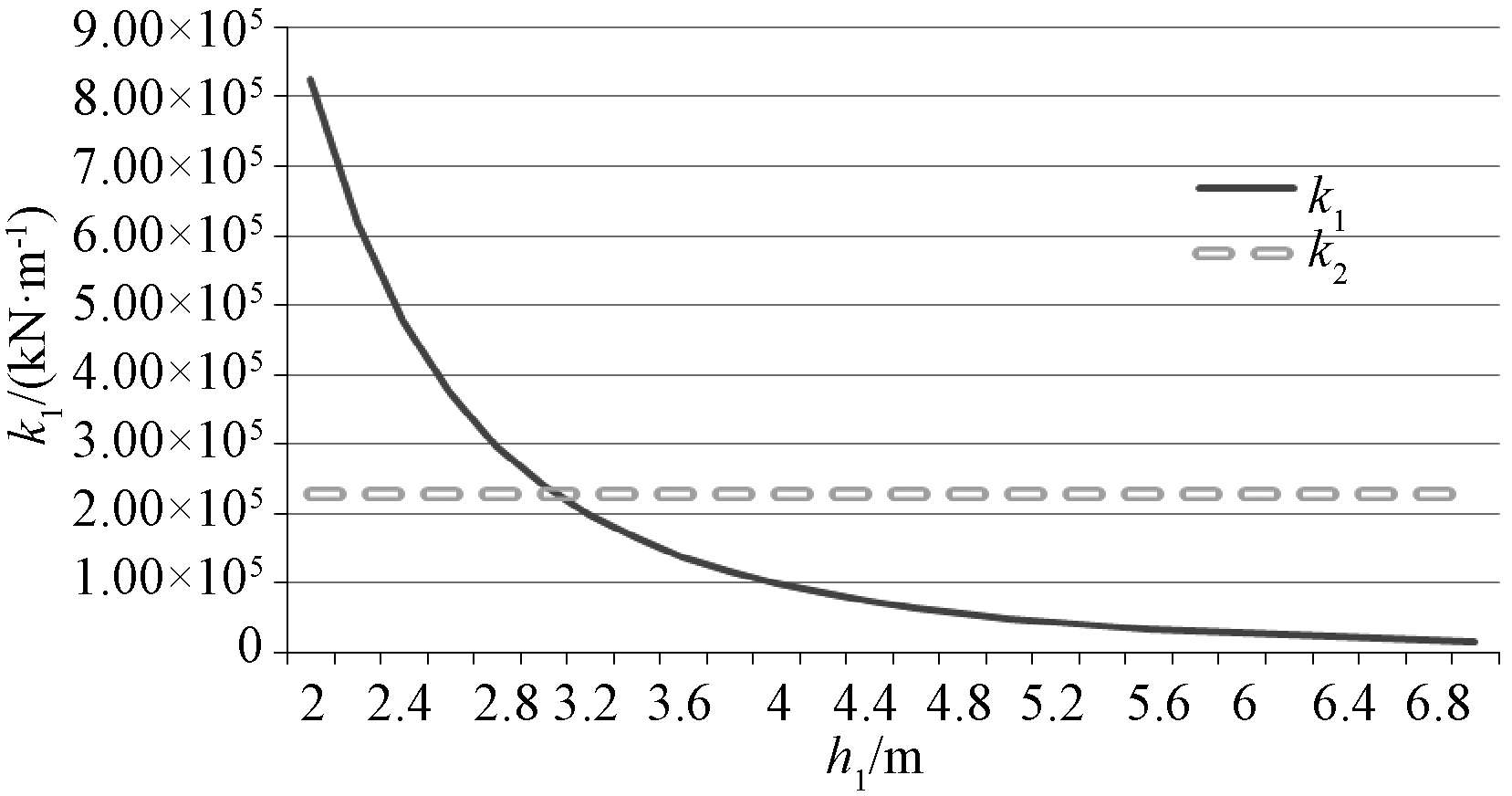
图4 h1与k1的关系示意图
Fig.4 Schematic diagram of the relationship between h1 and k1
文献[13]规定:当墩顶承受单位横向作用力H=1和单位力矩M=1时,该处水平位移δH和δHM及转角δM和δMH可按下列公式计算[14]:
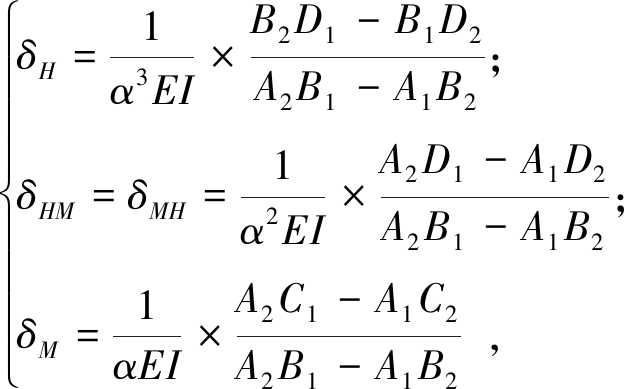
(7)
式中,Ai、Bi、Ci、Di为系数,在计算δH、δM、δHM和δMH时,根据文献[13]第P.0.8条查取:α为变形系数,经计算α=0.188 .
文献[13]的系数取值是针对当桩基嵌固在基岩中,而文中的KH、KM、KHM是将空心段的墩底和实心段的上部连接部位进行了弹簧转变模拟.根据文献[13]的规定和边界模拟可得系数的取值如下:A1=0.999 74,A2=-0.002 6,B1=0.499 96,B2=0.999 48,C1=0.125,C2=0.499 94,D1=0.020 83,D2=0.124 99.将数据代入式(7),可得:δH=4.38×10-9,δHM=δMH=1.86×10-9,δM=2.47×10-9,然后令h2=0时,k2=2.28×105kN/m,为了保证实心段和空心段的刚度实现过渡,令k1=k2,如图4中虚线所示,交点处对应的横坐标为h1=3.05 m.
同理对算例2分析,并将最后的分析结果和实桥数据进行对比,对比结果见表1.
表1 实心段长度分析结果对比
Tab.1 Comparison of the analytical results

算例计算长度/m实桥长度/m误差/%算例13.055.0039算例24.126.0031
注:误差=本文计算值和实桥数据差的绝对值/实桥数据.
由表1对比结果可知,依据本文计算原理推导出来的实心段计算长度和实桥数据的误差分别为39%和31%,误差较大的原因是工程实际中一般都是将实心段过渡长度选取的稍微偏大以方便施工及施工存在一定的偏差;同时结果也满足《云南省高速公路连续刚构桥梁关键技术指南》的取值范围规定,这说明本文计算原理和分析过程的正确性.
为了得出单肢空心薄壁墩墩底实心段计算长度的取值范围,通过Midas Civil软件对上述两个算例进行有限元分析.分析时保持桥墩高度不变,改变实心段的长度来验算空心段墩和实心段墩交接处的应力,计算对比结果见表2.
表2 交接部位应力对比结果
Tab.2 Transition section stress comparison results
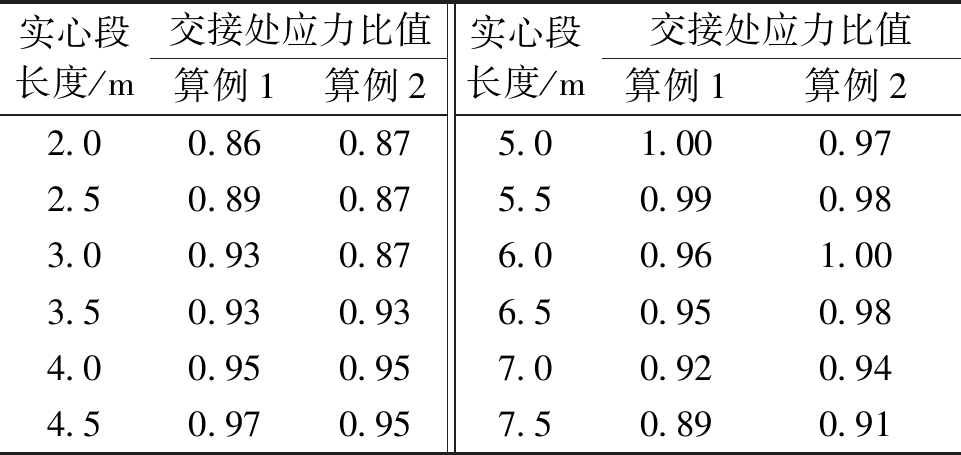
实心段长度/m交接处应力比值算例1算例2实心段长度/m交接处应力比值算例1算例22.00.860.875.01.000.972.50.890.875.50.990.983.00.930.876.00.961.003.50.930.936.50.950.984.00.950.957.00.920.944.50.970.957.50.890.91
注:表中数据为不同实心段取值长度与实桥实心段计算长度在交接处的应力比值.
由表2对比结果可得,实心段计算长度取不同值时,空心段和实心段交接部位的应力变化幅度不大,根据统计整理的国内外近百座连续刚构桥的单肢空心薄壁墩的实心段过渡长度数据[1],可以得出目前大部分墩底实心段计算长度的取值范围为3~6 m,因此根据本文的分析统计结果及已有的规定可以建议将墩底实心段计算长度取值范围3~6 m写入规范中,具体设计参考时可以上下稍微浮动.同时分析结果也证明了在空心段的墩底和实心段的上部相连接处采用平动约束、转动约束和平转动耦合约束弹簧来模拟连接处的约束作用是可行的.综上所述,笔者推导出的墩底实心段计算长度可以指导大跨连续刚构桥的设计及施工.
3 结论
(1)本文的计算原理和单肢空心薄壁墩墩底实心段计算长度的公式是正确的,对大跨连续刚构桥的设计及施工具有指导意义;
(2)在计算墩底实心段计算长度时,将空心段和实心段连接处用平动约束、转动约束和平转动耦合约束弹簧来模拟相互之间约束作用是可行的;
(3)建议将单肢空心薄壁墩墩底实心段计算长度取值范围3~6 m写入规范中来指导高墩的设计,具体设计参考时可以上下稍微浮动.
[1] 李艺林, 杨秀荣, 刘英. 连续刚构桥高跨比参数线性关系分析[J]. 河南城建学院学报, 2016, 25(6): 26-30.
[2] 李杰, 陈彬. 连续刚构桥顶推力计算与优化分析[J]. 郑州大学学报(工学版), 2013, 34(6): 85-89.
[3] KHODAIR A, HASSIOTI S. Rigidity of abutments in integral abutment bridges[J]. Structure and infrastructure engineering, 2013, 9(2): 151-160.
[4] 孙立刚. 柔性墩墩顶抗推刚度的计算[J]. 北方交通, 2012(2): 82-84.
[5] 张永水, 曹淑上. 连续刚构桥薄壁墩抗推刚度计算方法研究[J]. 中外公路, 2006, 26(3): 144-147.
[6] 刘志峰, 孙学先, 杨霞林. 考虑地基变形影响的高墩柱抗推刚度的解析方法[J]. 水利与建筑工程学报, 2007, 5(4): 63-66.
[7] 陈竹昌, 刘利民, 王建华. 承台刚度的研究[J]. 同济大学学报, 1999, 27(1): 29-33.
[8] 卢建峰, 蒋永生, 梁书亭. 依据刚性要求确定承台厚度[J]. 建筑结构, 2011, 41(增刊): 375-377.
[9] 王新玲, 杜琳, 黄伟东. 混合配筋预应力混凝土管桩抗弯刚度模型研究[J]. 郑州大学学报(工学版), 2013,34(6): 80-84.
[10] 邬晓光,李艺林,贺攀,等. 基于能量法分析大跨连续刚构桥高墩稳定性[J]. 铁道科学与工程学报,2017,14(2):290-295.
[11] 邬晓光,李艺林,何启龙,等. 基于频率合成法分析大跨连续刚构桥高墩横向振动基频[J]. 内蒙古大学学报(自然科学版),2017,48(2):213-218.
[12] 白青侠, 宋一凡. 高桥墩几何非线性的能量法[J]. 西安公路交通大学学报, 2001, 21(2): 50-52.
[13] 中交公路规划设计院有限公司. 公路桥涵地基与基础设计规范:JTG/D 63—2007[S]. 北京:人民交通出版社, 2007.
[14] 宁明哲, 李德建, 邹振兴. 变截面双肢薄壁高墩基础约束刚度动力识别方法[J]. 铁道科学与工程学报, 2013, 10(6): 74-78.