0 引言
钢管混凝土是由钢管与混凝土两种材料组合而成,两种材料之间的界面承载力的大小是保证两者协同工作的基础.现阶段对钢管混凝土粘结性能的研究采用推出试验.国内外学者对钢管混凝土的粘结滑移性能进行了试验研究和数值分析,邓洪洲等[1]通过推出试验研究提出了相关粘结强度计算公式;杨有福等[2]研究了矩形钢管自密实混凝土柱的粘结性能,认为采用自密实混凝土可以显著地增强钢管与混凝土间的界面粘结强度;康希良等[3]通过试验和理论分析得到了钢管与混凝土界面的粘结力传递规律,并回归得到粘结力计算模型;曲秀姝等[4-7]通过推出试验得到钢管混凝土柱之间的粘结力分布规律和界面承载力对钢管混凝土柱极限承载力的影响;刘永健等[8]提出了钢管与混凝土界面抗剪粘结应力和粘结滑移的本构关系,并认为粘结强度不受混凝土强度的影响.陈宗平等[9-12]通过推出试验得出了钢管与再生混凝土之间的粘结分布规律.但现阶段推出试验有一点不足,即钢管内部混凝土应力较低,混凝土横向膨胀较小,未考虑混凝土膨胀性对粘结能力的影响,而实际圆钢管混凝土柱中混凝土应力较高,混凝土膨胀性较大;同时钢管混凝土柱在节点处设有隔板及横穿钢管的钢筋等将限制钢管内混凝土的自由滑动.但现阶段推出试验中并未考虑这两种重要的因素,导致以往推出试验所得到的钢管与混凝土之间的粘结强度与实际工程中粘结能力并不相符.为使推出试验更接近实际工程中钢管混凝土柱的受力状态,笔者对钢管混凝土柱中的混凝土施加单调增加荷载,并对钢管进行推出试验.
1 试验概况
1.1 试件设计与制作
试验设计了3组共10个构件,根据混凝土应力水平和钢管内壁涂抹黄油情况,将试验构件分为3组.钢管混凝土柱试件构件具体参数见表1.
高应力下试件制作时,在钢管的一端焊接端板,在试件另一端与钢管直径相交处分别焊接一块耳板,耳板用于测量钢管和混凝土之间的相对滑移.为避免耳板处焊缝对钢管和混凝土之间粘结产生影响,浇筑混凝土时混凝土浇筑面距钢管有耳板的一端预留10 mm的空隙.低应力下试件制作时钢管两端不焊接端板和耳板,浇筑混凝土时混凝土浇筑面距钢管上端预留40 mm的空隙.具体如图1所示.
表1 试件主要参数
Tab.1 Main parameters of the specimens
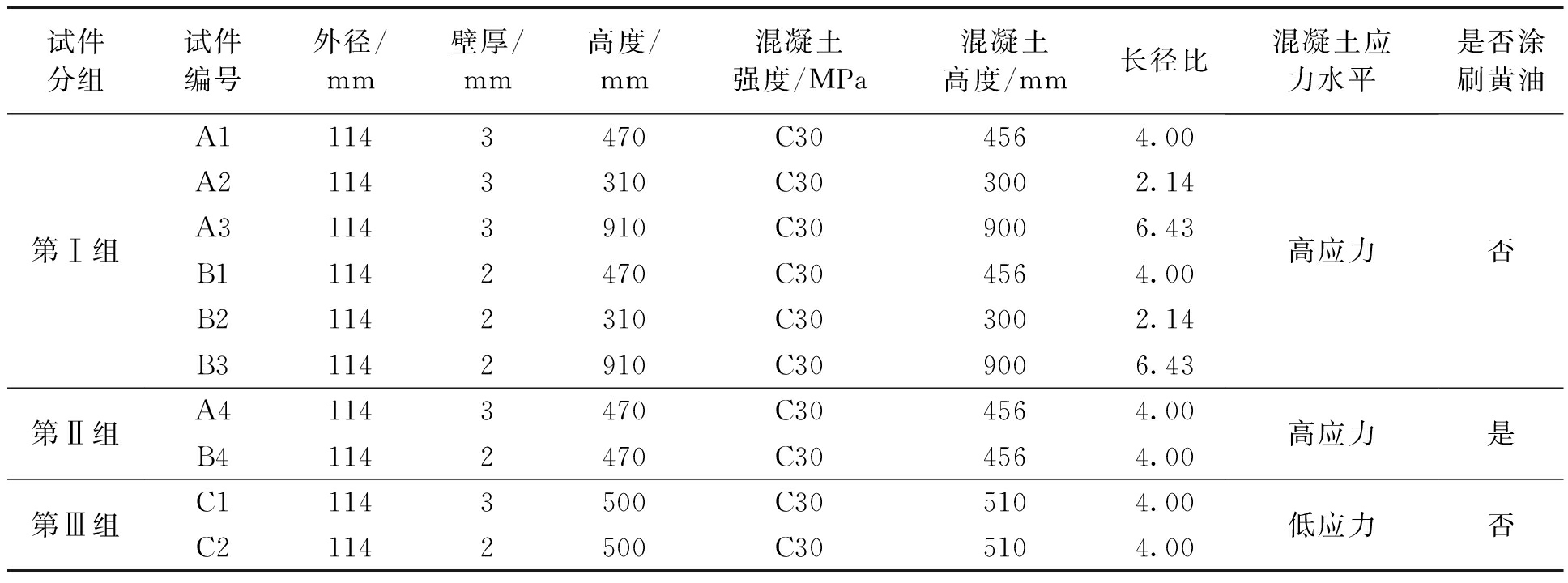
试件分组试件编号外径/mm壁厚/mm高度/mm混凝土强度/MPa混凝土高度/mm长径比混凝土应力水平是否涂刷黄油第Ⅰ组第Ⅱ组第Ⅲ组A11143470C304564.00A21143310C303002.14A31143910C309006.43B11142470C304564.00B21142310C303002.14B31142910C309006.43A41143470C304564.00B41142470C304564.00C11143500C305104.00C21142500C305104.00高应力高应力低应力否是否
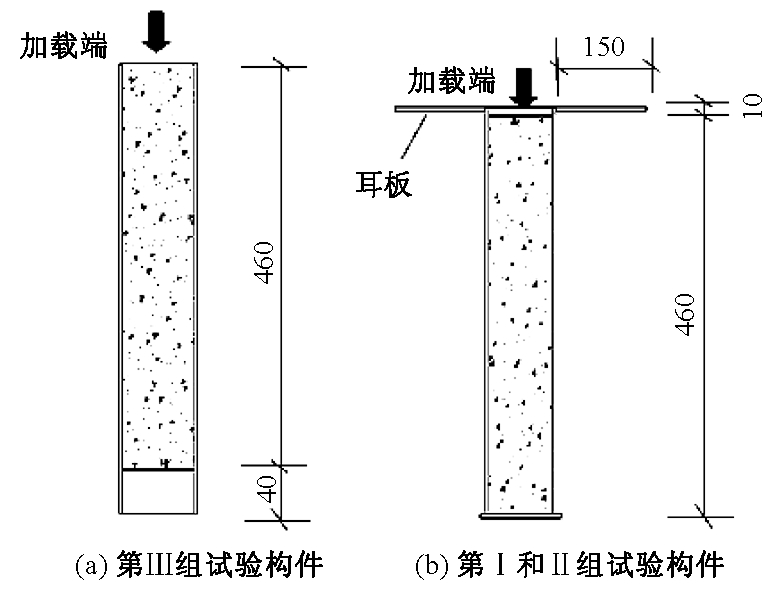
图1 试件的几何尺寸
Fig.1 The geometry of the specimens
1.2 材性试验
通过材性试验,钢材屈服强度为278 MPa,弹性模量为1.96×105 MPa.用标准试验方法在28 d龄期测得混凝土强度为29.4 MPa,弹性模量为3.01×104 MPa.
1.3 加载装置与加载制度
高应力下钢管混凝土柱推出试验采用2 000 kN的压力机加载,采用分级加载方式.对于高应力下推出试验每级荷载值为10 kN,当达到极限荷载值的90%时,采用缓慢连续加载的方式直至试验构件破坏;对于低应力下推出试验每级荷载值为5 kN,直至钢管与混凝土之间的粘结力达到极限承载力.推出试验加载装置如图2所示.

图2 推出试验加载装置
Fig.2 Push-out test loading device
1.4 测量内容和测点布置
在此次推出试验中,在圆钢管表面沿着轴向和环向粘贴较为密集的电阻应变计,测量推出过程中钢管纵向应变和环向应变.应变计布置如图3所示.
低应力下推出试验中,为了测量钢管和混凝土的相对位移,在压力机底部小车对角处布置两个位移计.高应力下的推出试验中,在钢管混凝土柱耳板下面布置两个位移计,测量钢管和混凝土的相对位移,除此之外,在压力机底部小车对角处布置两个位移计,测量钢管混凝土柱的压缩量.
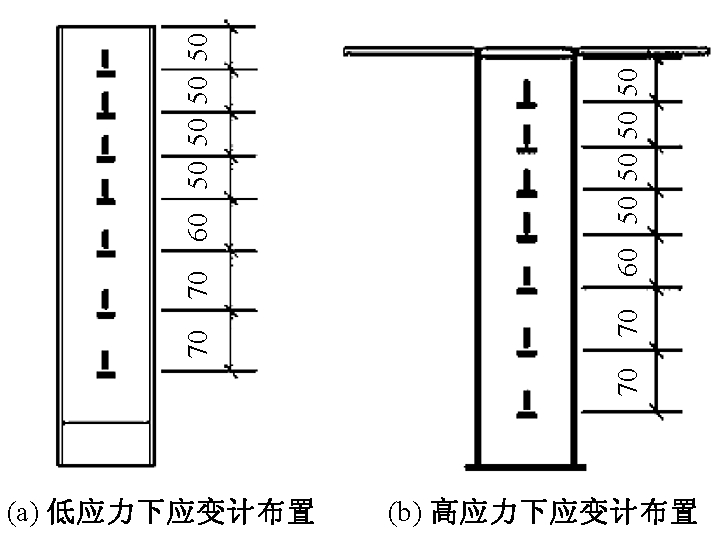
图3 钢管应变计的布置
Fig.3 Steel strain gauge layout
2 试验结果及分析
2.1 试验现象
低应力下推出试验中,试件C1和C2在加载初期,钢管与混凝土基本没有相对位移.随着荷载的增加,位移缓慢增加,位移偶尔会以跳跃的方式增加.当加载到极限荷载的80%~90%时,钢管与混凝土发生相对位移,并发出清脆的响声;当达到极限荷载后,位移开始快速增加,同时荷载缓慢下降,直到加载过程结束.在加载过程中,混凝土没出现压坏现象,钢管也未屈曲.钢管与混凝土之间有较明显摩擦痕迹,破坏模式如图4(a)所示.
高应力下推出试验加载初期,钢管和混凝土基本没有相对位移.随着荷载的增加,混凝土压缩量缓慢增加,钢管与混凝土的相对位移也开始增加.钢管与混凝土相对位移在加载过程中会间隔出现跳跃增加现象.当加载到极限荷载的85%~100%时,钢管表面氧化皮逐渐开裂剥落,表面微微鼓曲,同时位移增加较快.当达到极限荷载后,位移开始快速增加,钢管中部发生较大屈曲,同时荷载开始缓慢下降.钢管与混凝土之间摩擦痕迹不明显,构件的破坏模式如图4(b)所示.

图4 推出试验构件破坏模式
Fig.4 Failure mode of push-out test components
2.2 荷载-位移曲线
低应力下推出试验中,荷载小于弹性极限荷载时,荷载-位移成线性关系,在此过程中混凝土与钢管之间的胶结力逐渐消失,而两者之间的摩擦力和机械咬合力逐渐增加;在达到弹性极限荷载时,钢管与混凝土之间只剩摩擦力和机械咬合力,荷载-位移曲线呈现非线性关系变化;当相对位移增加到大约是5 mm左右时,钢管与混凝土之间的粘结力到达极限值,钢管与混凝土之间的相对位移增加较快,随后荷载开始缓慢下降,但下降幅度不大.荷载-位移曲线如图5(a)所示.
高应力下推出试验的荷载-位移曲线与钢管混凝土柱的荷载-位移曲线变化趋势基本相同,如图5(b)所示.
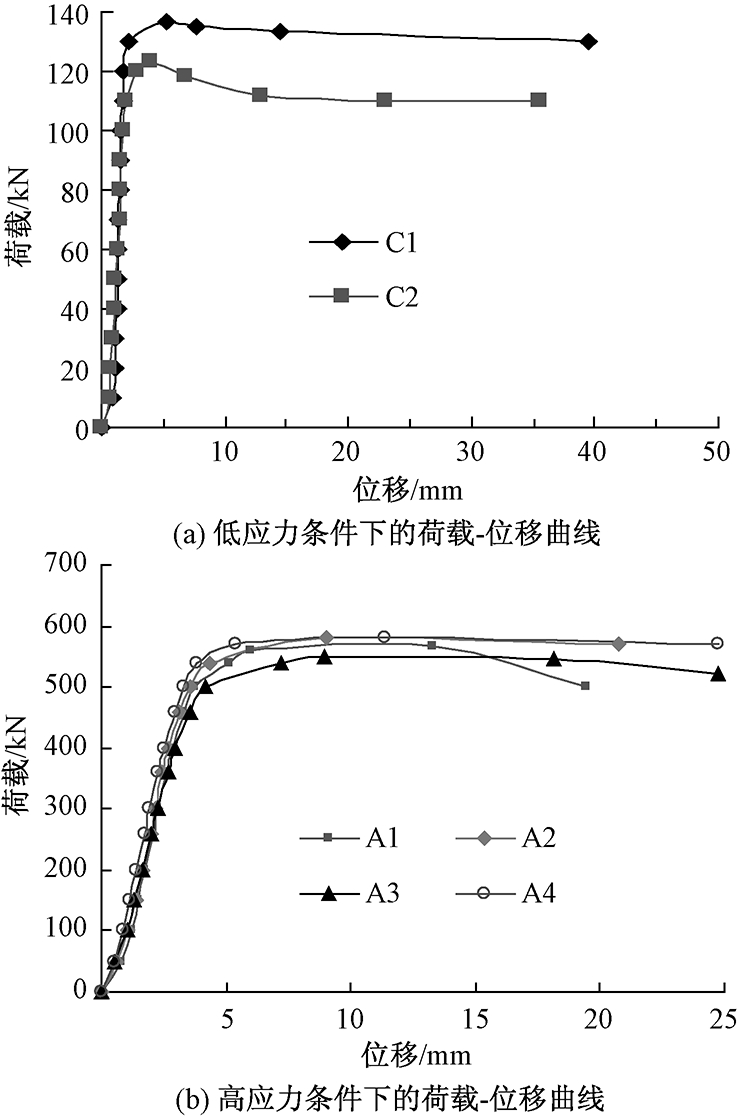
图5 推出试验荷载-位移曲线
Fig.5 Push-out test load-displacement curve
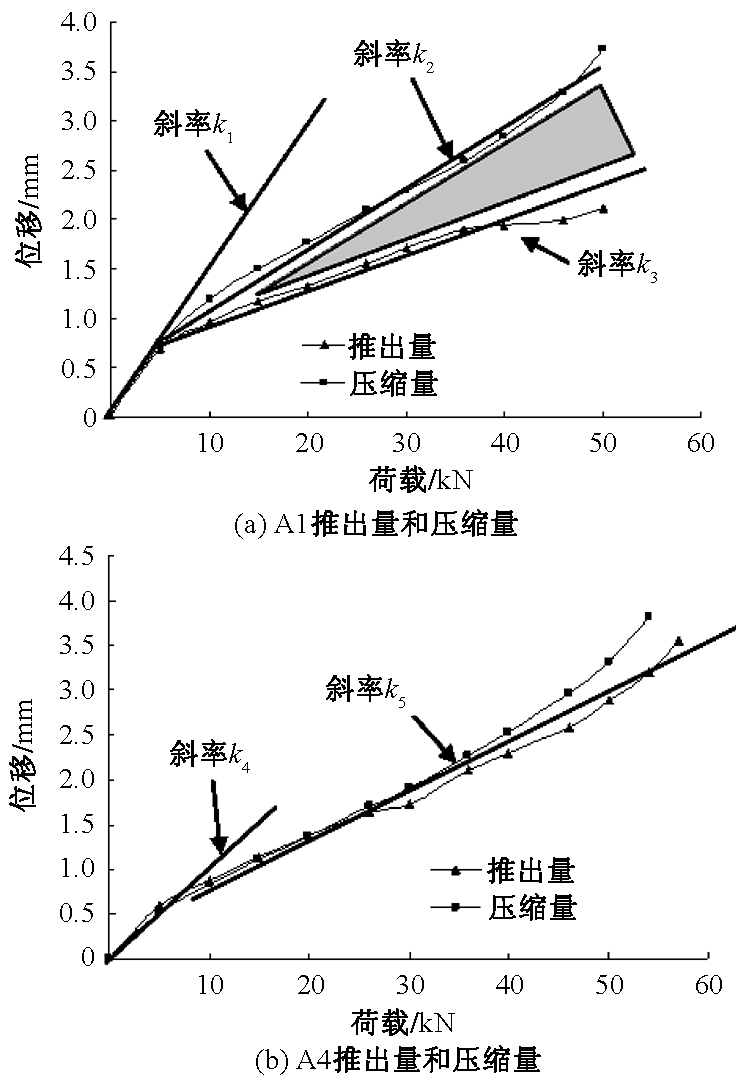
图6 弹性荷载条件下推出量和压缩量
Fig.6 The amount of pushout and the amount of compression under elastic loading conditions
高应力下荷载大于弹性极限荷载时,钢管将产生较大的变形,测量钢管与混凝土之间相对位移的耳板将产生较大的变形,量测的准确性受到较大的影响.因此,图6只绘出弹性荷载条件下推出量和压缩量之间的关系.其中压缩量是指在压力作用下混凝土的压缩值;推出量是指钢管端部由耳板测量的钢管向上的位移量.以试件A1和试件A4为例说明高应力下的整个推出过程.
图6(a)中,试件A1在荷载小于50 kN时,压缩量和推出量以斜率k1增加较快;当荷载大于50 kN时,压缩量和推出量将分别以不同的斜率k2和k3线性增加,压缩量的增加速度比推出量的增加速度快.压缩量曲线和推出量曲线之间的阴影即为在不同荷载条件下钢管与混凝土的共同变形量.从图7(a)可知,荷载越大,钢管与混凝土的共同变形量也增大.
试件A4在荷载小于50 kN时,压缩量和推出量以斜率k4增加较快;而当荷载大于50 kN时,试件A4的压缩量和推出量以相同的斜率k5线性增加,压缩量和推出量的增加速度基本相同.引起A1和A4不同变形的原因是试件A4钢管内表面涂抹黄油减小钢管与混凝土之间的摩擦力,摩擦力的减小使得钢管与混凝土之间的共同变形量减小,而使得钢管推出量与混凝土压缩量基本相同.
2.3 应变沿高度的分布
试件C1钢管外表面纵向和环向应变沿钢管高度的分布曲线如图7所示.
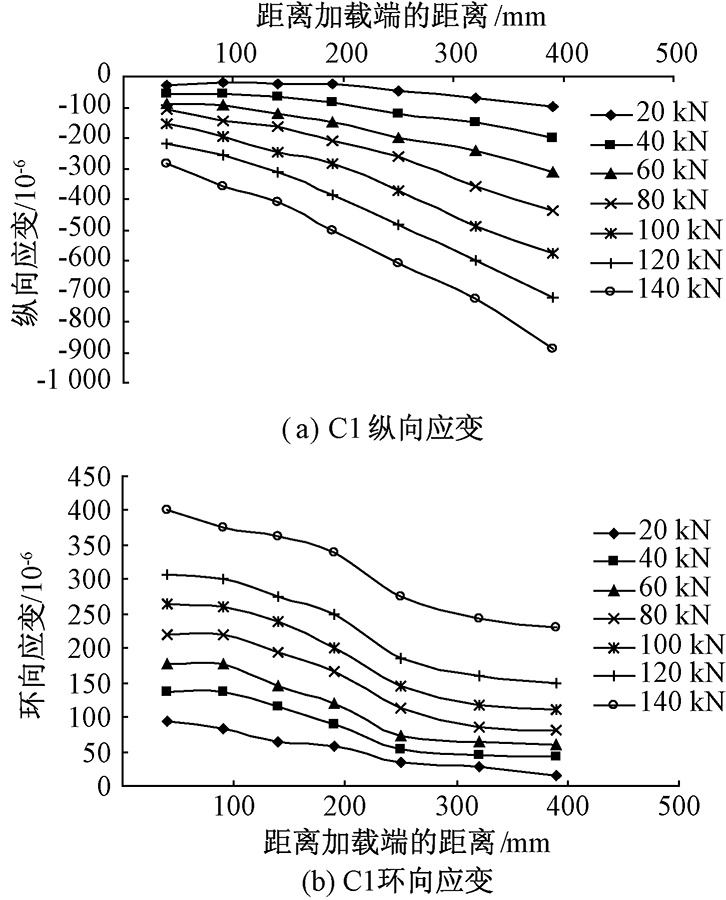
图7 C1钢管外表面纵向和环向应变沿钢管高度的分布
Fig.7 C1 steel pipe outside surface longitudinal and annular strain distribution along the pipe
从图7可知,在低应力推出试验中,钢管混凝土柱处于弹性阶段.随着距离加载端距离增加,由于混凝土与钢管之间的粘结力的累积使钢管的纵向应变增加,而混凝土应力减小,混凝土横向膨胀减小,导致钢管环向应变逐渐减小.加载过程中,钢管的纵向和环向应变未达到屈服应变.钢管的环向应变比较小,最大应变小于400 με.
以试件A1为例说明在高应力下推出试验中钢管表面各测点应变的变化如图8所示.
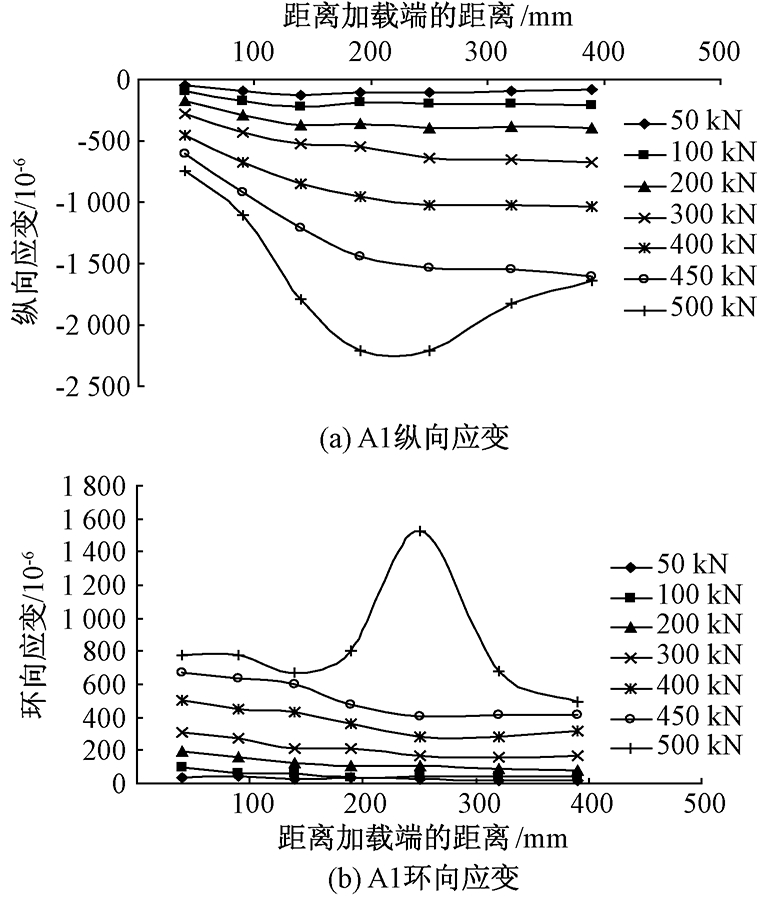
图8 A1钢管表面测点应变
Fig.8 The strain of A1 steel surface measurement points
从图8可知,在达到弹性极限荷载前,随着距离加载端的距离增加,钢管的纵向应变增加,钢管的环向应变减小,其原因与低应力下推出试验相同.但达到弹性极限荷载之后,钢管表面中部测点纵向和环向应变基本都达到屈服应变.钢管屈服使得钢管上部的力无法有效地传递到钢管的下部,因此,距离屈服点下面钢管的纵向应变增加较小.
2.4 参数变化对纵向和环向应变影响
长径比、壁厚和混凝土应力水平等参数对钢管混凝土柱的纵向和环向应变都有一定的影响.
通过分析可知,钢管壁厚只会影响纵向和环向应变的大小,不会影响纵向和环向应变的变化趋势.即壁厚只会影响钢管与混凝土之间粘结力的大小,并不会影响粘结力的变化趋势.
从图9可知,长径比越大纵向和环向应变越小,而且钢管距离加载端越远的纵向应变增加较为缓慢,钢管中部应变平缓段越长.这是由于加载端钢管与混凝土之间发生相对滑动,上部钢管的应力得到释放,故应力变化较大,中下部钢管相对混凝土的滑动较小或只有相对位移的趋势,应力得不到释放,故应变变化不大.从图9(a)可以看出,长径比对纵向应变影响显著.即对钢管与混凝土之间的粘结力影响显著.
从图10可知,高应力下钢管的纵向应变和环向应变都要高于低应力下钢管的应变,即高应力下钢管与混凝土之间的粘结力高于低应力下钢管与混凝土之间的粘结力.低应力下纵向和环向应变近似于直线变化,并且两种情况下纵向应变和环向应变变化趋势也不相同.因此应力水平对纵向和环向应变影响较大,即对钢管和混凝土之间的粘结力有较大影响.
综上所述可知,长细比和混凝土应力水平对钢管与混凝土之间的粘结力有较大影响;壁厚只影响钢管与混凝土之间的粘结力的大小.
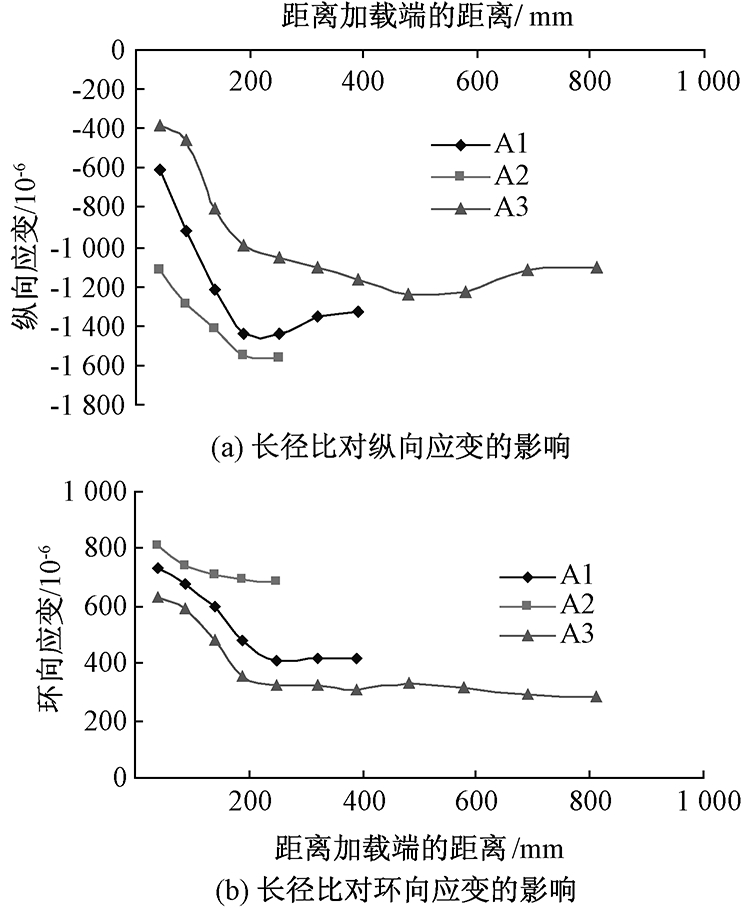
图9 长径比对钢管应变的影响
Fig.9 The influence of slenderness ratio on steel pipe strain
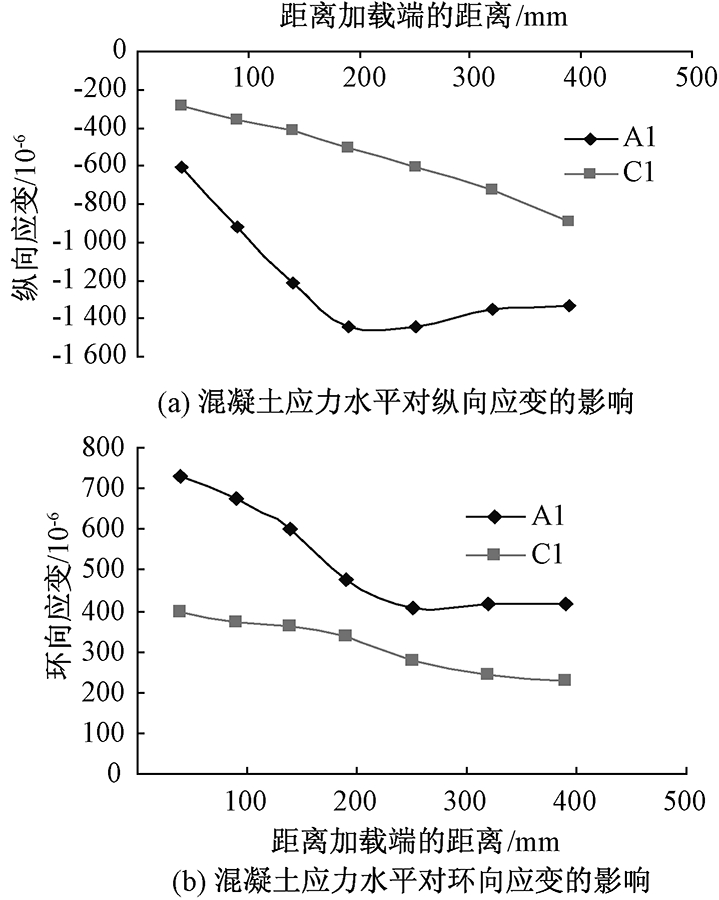
图10 混凝土应力水平对钢管应变的影响
Fig.10 The influence of the concrete stress level on steel tube strain
2.5 钢管与混凝土的粘结强度
文献[3,12]中钢管的粘结强度通过试验数据数值回归的方式得到,在公式中并未考虑混凝土膨胀性的影响因素.混凝土膨胀性对钢管与混凝土之间的相互作用力有较大的影响,特别是摩擦力.当钢管与混凝土之间产生相对滑移时胶结力已经消失.同时在浇筑混凝土时会充分振捣,在钢管壁会粘结一层水泥砂浆,使得混凝土表面较为平整,钢管与混凝土之间的机械咬合力较小,可以忽略不计.因此,在钢管达到弹性荷载之前,计算钢管与混凝土之间的粘结力时,只考虑它们之间的摩擦力.
计算摩擦力时,首先确定钢管对混凝土的约束作用力p(x),为计算p(x)做出如下假定:①钢管的环向应变沿钢管的表面均匀分布;②钢管对混凝土之间的约束作用力沿钢管环向均匀分布.
上述假定可以通过钢管表面测点的环向应变,计算钢管的环向应力:
σ(x)=ε(x)·Es,
(1)
式中:Es为钢管的弹性模量;ε(x)为钢管表面测点的应变.
钢管对混凝土的约束作用力p(x):
(2)
式中:t和D分别为钢管的厚度和内径.
钢管与混凝土之间的摩擦力f(x):
f(x)=μ·p(x),
(3)
式中:μ为钢管与混凝土之间的滑动摩擦系数.
通过式(1)~(3)的计算,在低应力下推出试验中,钢管与混凝土之间的剪应力从加载端到自由端逐渐减小,剪应力的最大值都小于1.06 MPa,其余点处的剪应力都小于1 MPa,钢管通过与混凝土之间的剪应力承担全部的推出荷载141 kN;在高应力下推出试验中,由于混凝土的横向膨胀,钢管对混凝土约束作用力较大,钢管与混凝土之间的剪应力最大值达到1.79 MPa,剪应力的最小值1.08 MPa,钢管通过与混凝土之间的剪应力承担部分的推出荷载,其承担的荷载值为231 kN,达到弹性极限荷载的51%.
从上述分析可知:钢管对混凝土的约束作用力对钢管与混凝土之间剪应力影响较大,是钢管与混凝土内力分配中不可忽视的重要因素.
3 结论
(1)两种条件下推出试验中,钢管混凝土柱的破坏模式不同.在低应力条件下推出试验中钢管表面没有屈服,钢管与混凝土发生较大相对滑移而破坏;在高应力条件下推出试验中钢管与混凝土发生相对滑移较小,钢管表面屈曲而破坏.
(2)两种条件下荷载-位移曲线变化趋势相同,但高应力条件下推出试验中钢管承担的推出荷载值比低应力条件下承担的推出荷载值大.
(3)长径比和混凝土应力水平对钢管与混凝土之间的剪切应力有较大影响.壁厚对钢管与混凝土之间的剪切应力影响较小.
参考文献:
[1] 邓洪洲, 傅鹏程. 矩形钢管和混凝土之间的粘结性能试验[J]. 特种结构,2005,22(1):50-52.
[2] 杨有福,韩林海. 矩形钢管自密实混凝土的钢管-混凝土界面粘结性能研究[J]. 工业建筑,2006,36(11): 32-36.
[3] 康希良. 钢管混凝土组合力学性能及粘结滑移性能研究[D]. 西安:西安建筑科技大学土木工程学院,2007: 67-140.
[4] QU X S,CHEN Z H.Load-reversed push-out tests on rectangular CFST columns[J]. Journal of constructional steel research,2013,81(3):35-43.
[5] CHANG X, HUANG C K, JIANG D C, et al. Push-out test of pre-stressing concrete filled circular steel tube columns by means of expensive cement[J]. Construction and building material, 2009,81(23):491-497.
[6] SHAKIR K H. Pushout strength of concrete-filled steel hollow sections[J]. The structural engineer, 1993,71(13):230-233.
[7] SHAKIR K H. Resistance of concrete-filled steel hollow tubes to push-out forces[J]. The structural engineer, 1993,71(13):234-243.
[8] 刘永健,刘君平. 钢管混凝土界面抗剪粘结滑移力学性能试验[J].广西大学学报(自然科学版),2010,35(1):17-23.
[9] 陈宗平,徐金俊,郑海华,等. 再生混凝土基本力学性能试验及应力-应变本构关系[J].建筑材料学报,2013,16(1):24-32.
[10] 徐金俊,陈宗平,薛建阳,等. 圆钢管再生混凝土界面粘结失效的推出试验研究[J]. 建筑结构学报,2013,34(7):148-157.
[11] 陈宗平,徐金俊,薛建阳,等. 钢管再生混凝土粘结滑移推出试验及粘结强度计算[J]. 土木工程学报,2013,46(3):49-58.
[12] 蔡绍怀. 现代钢管混凝土结构[M]. 北京:人民交通出版社, 2003:229-232.