0 引言
由于人们的无线接入需求不断增长、可分配的频谱资源有限、授权频谱利用率低及频谱利用情况极不平衡等情况的发生，认知无线电技术应运而生，机会频谱接入是认知无线电技术的一个热门方向[1-3]，是解决无线频谱资源短缺、频谱利用率低的有效方法.
纵观现有的大部分研究，往往是考虑到最小化系统干扰，或者最大化系统吞吐量[4-6].随着通信技术的飞速发展，结合用户需求为其分配资源成为一个热点问题.因此，近年来从用户角度出发研究基于用户需求的机会频谱接入问题激发了人们的研究兴趣，并出现了一些研究成果[7-9].文献[7-9]均借助博弈论的方法，构建效用函数时同时考虑用户自身和相邻用户的满意度，从而达到用户满意度的全局最优.文献[7]根据用户吞吐量大小衡量用户满意度；文献[8]将业务分为脆性业务、流媒体业务、弹性业务，根据用户不同的业务类型采用不同的体验函数衡量用户体验水平；文献[9]则同时考虑频谱接入、功率分配和用户调度3个因素，衡量小区满意度水平.
上述文献中，目标是合理分配信道和功率资源，使每个用户尽可能达到自己的需求，而忽略了用户之间相互干扰，这些干扰将导致网络性能下降，进而影响用户体验，因此在考虑用户需求的同时将干扰作为约束条件是必要的.为此，笔者在文献[7]的基础上，考虑每个用户的干扰，构建基于满意度的效用函数，其目的是在最小化认知用户自身干扰量的同时兼顾满意度，提高系统总体性能.文中证明了该优化问题是一种精确势能博弈，且该博弈至少具有一个纯策略纳什均衡点，并且其纳什均衡点是全局最优解.仿真结果表明，相对于文献[7],本文方法考虑认知用户干扰因素后，在网络总干扰显著降低的同时，获得了更高的公平性.
1 系统模型和问题描述
1.1 系统模型和基于用户需求的满意度函数
考虑一个包含N个认知用户和M个授权信道的认知无线电动态频谱接入系统.N个认知用户在授权用户不使用授权信道时接入信道.M个授权信道可以随机被授权用户使用.这里用Jn={j∈N;(j,n)∈εd},表示用户n的相邻用户集合，即干扰用户集合.图1举例说明了两个授权用户；4个授权信道{1，2，3，4}；4个认知用户的认知无线网络分布及对应的干扰图.用T={N,εd}来描述用户之间的干扰关系,这里顶点集N表示认知用户的集合，边缘集εd={ (i，j)；‖di，dj‖≤δ，i,j≠i∈N}表示干扰边的集合.如果两个认知用户之间存在边缘，当这两个用户同时使用相同的信道时，将产生干扰.
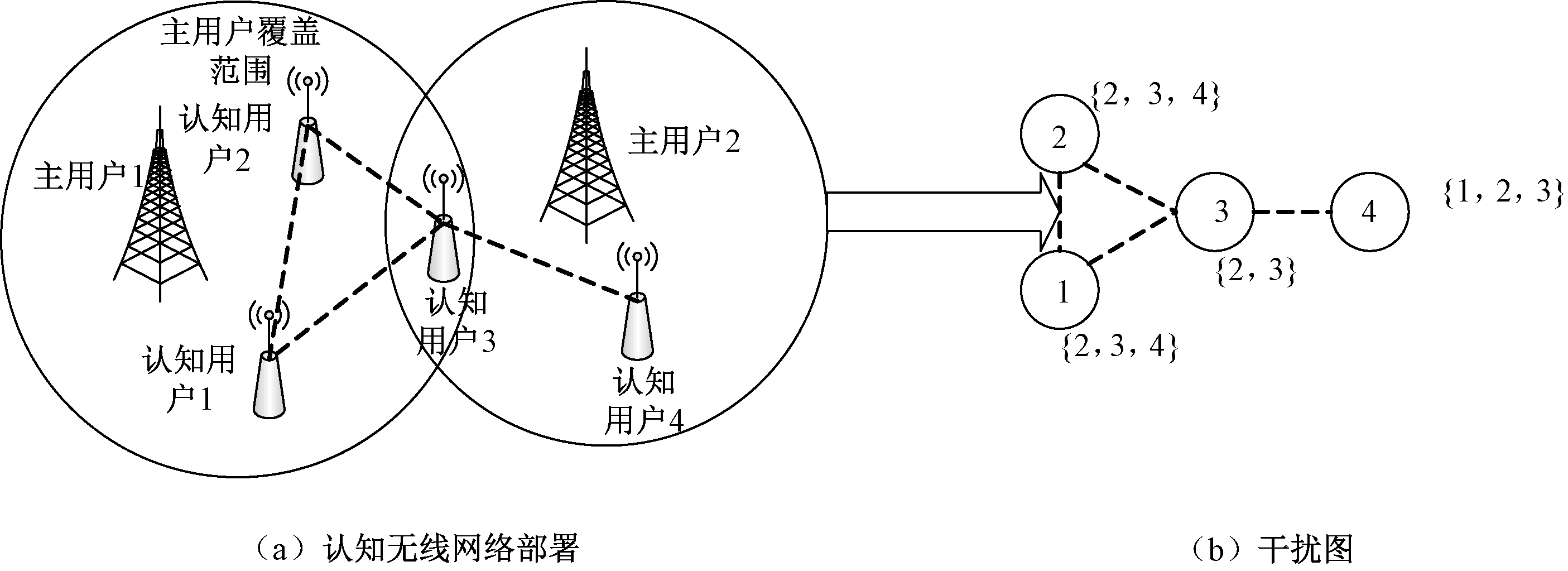
图1 认知无线网络分布及其干扰关系图例
Fig.1 Example of the considered cognitive radio network and interference graph
用户n可用的信道集合可以表示为：
An={m∈M}.
(1)
由图1(b)可知：A1=A2={2,4}，A3={2}，A4={1,2,3}.
文献[7]中引入的满意度函数为：
(2)
式中：rn表示实际分配给用户的资源，本文为认知用户在多条信道上传输数据时的总吞吐量; dn表示用户实际所需吞吐量大小；c用来调节曲线的坡度.由式(2)分析可知：c较小时用户需要获取更多的吞吐量才能获得较高的满意度；c较大时用户满意度虽然较大，但初始阶段用户即使获得一定量的吞吐量时满意度依然较低.c的取值不能很好地表示出用户满意度、实际分配的吞吐量和所需吞吐量三者之间的关系.这里考虑选取一种新的与实际分配给用户的资源大小直接相关的满意度函数.
采用文献[9]中的满意度函数如下：
(3)
式中：rn表示实际分配给用户的资源大小；dn表示用户需要的资源大小.
由该满意度函数可知，随着分配给用户的资源增加，满意度线性增大；当分配给用户的资源增大到用户所需资源大小时满意度变为1，此后如果分配给用户的资源继续增多时满意度不再增加.
1.2 问题描述
本文研究的问题为干扰约束下基于用户需求的多信道机会频谱接入优化问题.关于此问题文献[7]给出了基于用户需求的优化问题，但实际应用中用户之间存在较大干扰，也会对网络的接入产生影响.因此，笔者在文献[7]的基础上，构建干扰约束下基于用户需求的多信道机会频谱接入优化问题.
在式(1)中，当An≠φ时，假定用户n选择一组信道集合an⊂An传输数据，即用户n在这一组信道上传输数据.
(4)
式中：
表示用户n选择的信道集合中的第i条信道.用户n在全体用户信道选择a=(a1,a2,…,aN)的情况下的吞吐量为:
(5)
式中：f(k)为k个用户竞争一个单独的信道时的吞吐量损失函数；
为信道的传输速率；
为用户n的相邻用户中与用户n竞争信道的用户数目；求和式表明用户n的总吞吐量为用户n选择的信道集合中的各个信道的吞吐量之和.
(6)
文献[7]中认知用户n的收益函数的度量标准就是其满意度函数.改进后的效用函数如式(7)所示，等式右边第一项为认知用户n的满意度，可以理解为其获得的收益，第二项为其他用户对认知用户n的干扰和，可以理解为付出的代价. 因此，用户n的净收益函数可以表示为式(8).
(7)
(8)
本文研究的目标是最大化整个网络的净收益函数，即认知用户在获得较高的满意度时将用户间干扰降至最小，在满意度和干扰之间进行折中，优化问题如式(9)所示:
P:argmax U0(a).
(9)
2 基于博弈论的分布式认知网络多信道机会频谱接入问题
由于该网络模型没有中心控制器，这就促使我们对这个问题建立博弈模型求解，博弈论是研究没有中心控制器的分布式信道选择问题的有效工具.小节以(7)式为基础，充分利用认知用户间的局部相互作用关系，构建效用函数时同时考虑用户自身及其相邻用户的净收益，并证明了该博弈模型是至少存在一个纳什均衡[10]的精确势能博弈，且其纳什均衡点能够最大化系统净收益.
2.1 效用函数
定义认知用户∀n∈N效用函数如下：
(10)
式中：aJn∈PAJn表示认知用户n的相邻用户策略集合；In={k∈Jn:ak∩An≠φ} ,表示认知用户n的相邻用户中可能和其竞争信道的认知用户集合；a0=φ表示用户n不参与竞争信道；aJk\n表示当用户n放弃竞争信道时用户k的相邻用户的策略集合.
由式(10)可以看出，认知用户n的效用函数包括自身和其相邻用户的收益.与文献[7]不同的是，每个用户的收益不仅考虑其满意度，还考虑了干扰，使得其在最小化自身干扰量的同时兼顾满意度.
因此，该博弈可以描述如下:
G:maxUn(an,aJn).
(11)
2.2 纳什均衡解的分析
定理1 G是至少具备一个纳什均衡的精确势能博弈，并且其纳什均衡点是P的最优解[11].
证明 构建势能函数如下：
(12)
由上式可以看出,势能函数就是网络的净收益.
假设认知用户n单方面从信道an改变到信道
因此势能函数的变化值为：
Φ
(13)
用户n的行为改变仅仅影响它的相邻用户中一部分可能和用户n竞争信道的用户，可以得到下式：
∀k∈N\Jn,k≠n；
(14)
∀k∈Jn\In,k≠n.
(15)
认知用户n单方面从信道an改变到信道
效用函数的变化值为：
(16)
(17)
根据式(17)可以看出，该博弈是精确势能博弈.精确势能博弈有如下的性质: 任何精确势能博弈至少具有一个纯策略纳什均衡点；势能函数全局或局部最大点是该精确势能博弈的纳什均衡，也就是说，势能函数最优解就是该纯策略纳什均衡点.
定理得证.
3 数值仿真与分析
本节运用常见的学习算法Spatial Adaptive Play(SAP)[4]进行数值仿真.因为文献[7]也采用该算法仿真，仿真的过程中已经计算了用户间干扰，而本文只是将计算得到的干扰值构建在效用函数中，所以本文算法和原算法复杂度相同.
基本仿真参数参考文献[7],设置如下:认知用户个数 N=20，信道个数M=3，假定所有信道具有相同的传输速率1 Mb/s.由于不同的用户所需的传输速率一般不同，这里设置70%的认知用户所需的传输速率分布在[0,1)，25%的认知用户所需的传输速率分布在[1,2)，5%的认知用户所需的传输速率分布在[2,3].干扰图如图2所示，每个小圆表示一个认知链路.
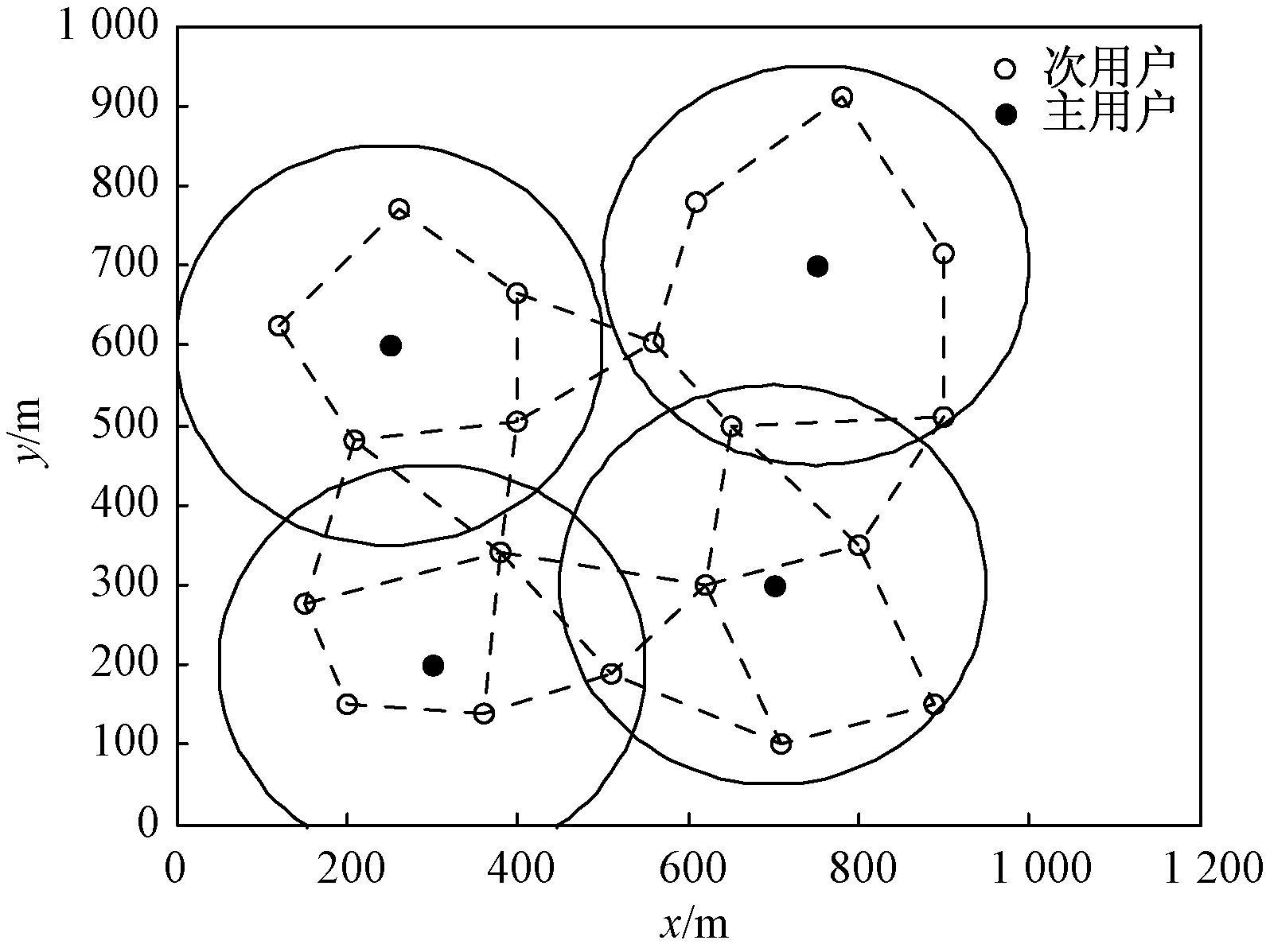
图2 干扰图
Fig.2 Interference graph
图3纵坐标表示整个网络的干扰水平.可以看出，在考虑干扰因素以后，当迭代次数达到75次时，全局干扰衰减为0，即最终达到系统的稳定状态.这是因为，随着各用户的策略更新，每个用户的干扰值越来越小，从而使得系统中的总干扰在不断减小，当达到纳什均衡状态时，所有用户都不再改变其策略，全局干扰达到最小值且不再变化.而采用原文献[7]中的方法得到的结果是:随着迭代次数的增加，整个网络干扰值依然很大.这是由于认知用户为了得到较高的满意度会选择多条信道传输信息，此时并没有针对性考虑干扰因素，导致整个网络的干扰很大.
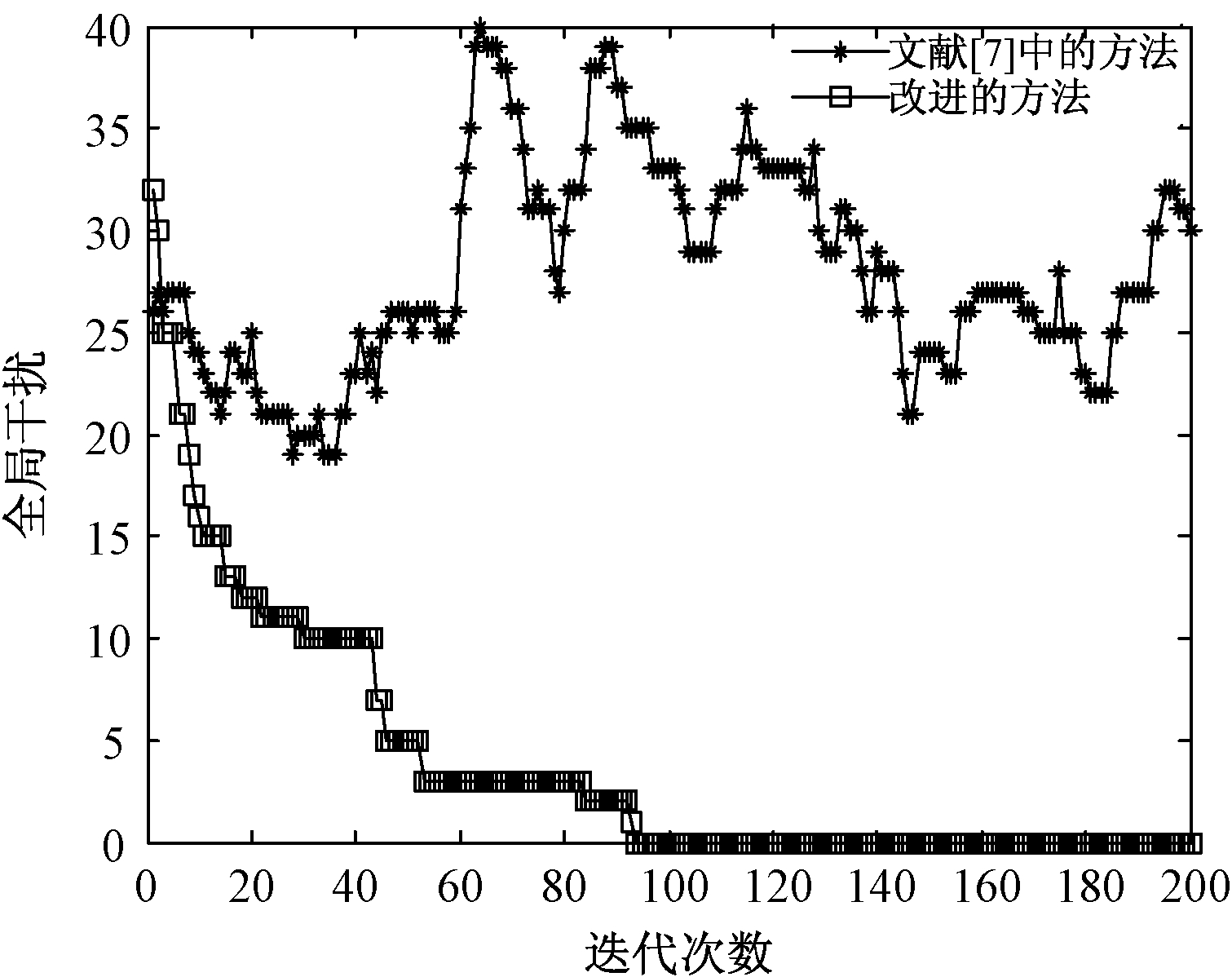
图3 总干扰对比
Fig.3 Comparison of the total interference
为了使比较更有意义，这里统一采用本文算法的满意度函数.随着分配给用户的资源增大，用户满意度线性增大，当分配给用户的资源增大到用户所需资源时用户满意度变为1.由图4可以看出，随着授权信道空闲概率的增加，用户平均满意度逐渐增加.因为，随着授权信道空闲概率增大，认知用户可用信道资源增加，用户平均满意度必然增加.由图4还可以看出，考虑干扰因素以后用户满意度只是略微低于不考虑干扰时的用户满意度，这是因为考虑干扰因素以后，认知用户会在降低干扰的同时提高满意度，即兼顾两个因素以提高网络的整体性能.
公平度是无线通信比较关注的问题，这里用Jain公平指数(Jfi)研究公平度问题，Jfi的变化从0～1，Jfi越大，公平性越高，资源分配就越公平.由图5可以看出，Jfi随着授权信道空闲概率的增大而增大，因为授权信道空闲概率较小时，空闲信道资源较少，仅能满足少量认知用户，因此 Jfi较小.授权信道空闲概率较大时，空闲信道资源增加，在满足更多的认知用户的同时提高了各个用户的满意度，使得Jfi增加.由图5还可以看出，采用改进的方法的Jfi比原文献的高，资源分配更加公平.
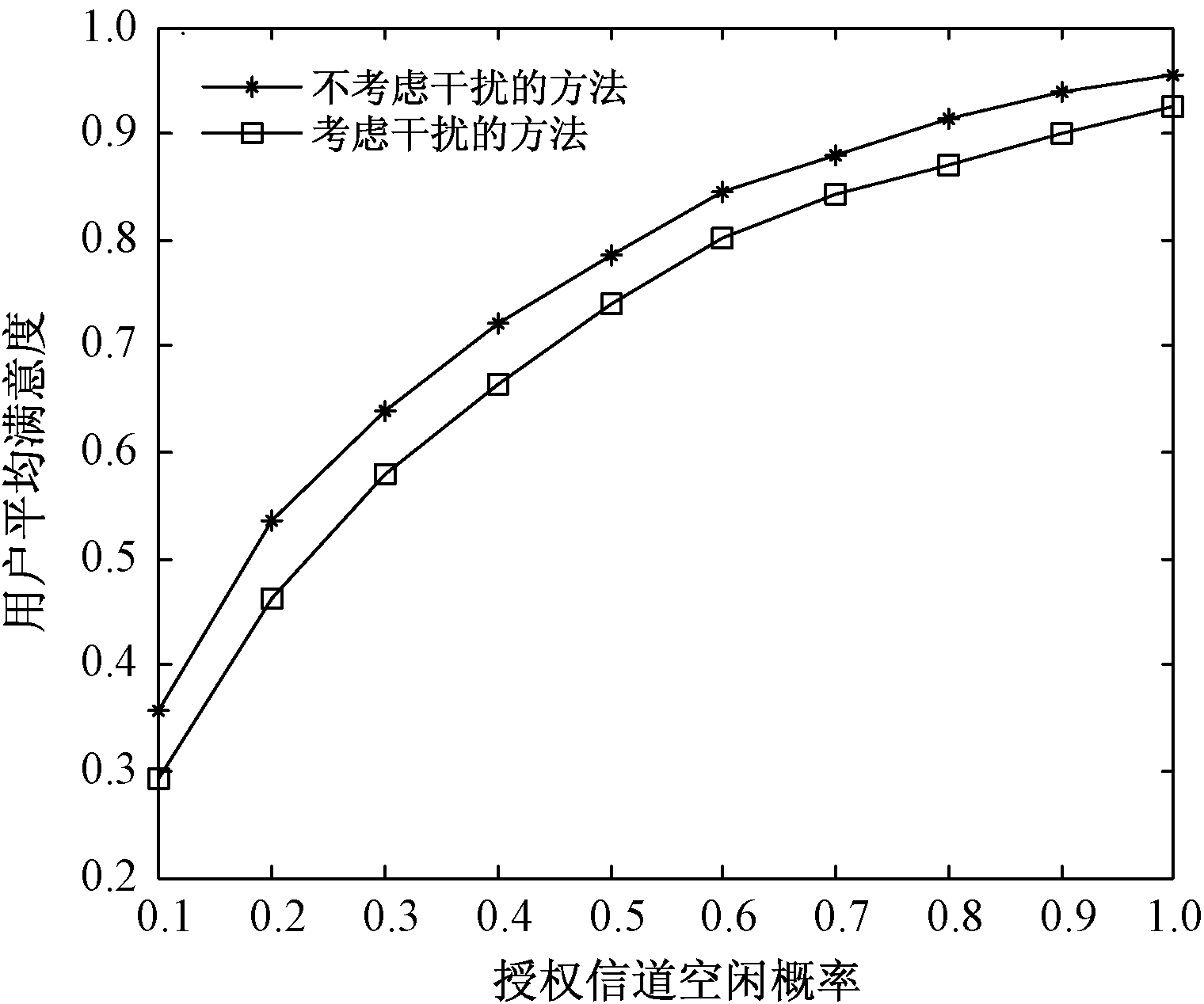
图4 用户平均满意度比较
Fig.4 Comparison of the users’ average satisfaction
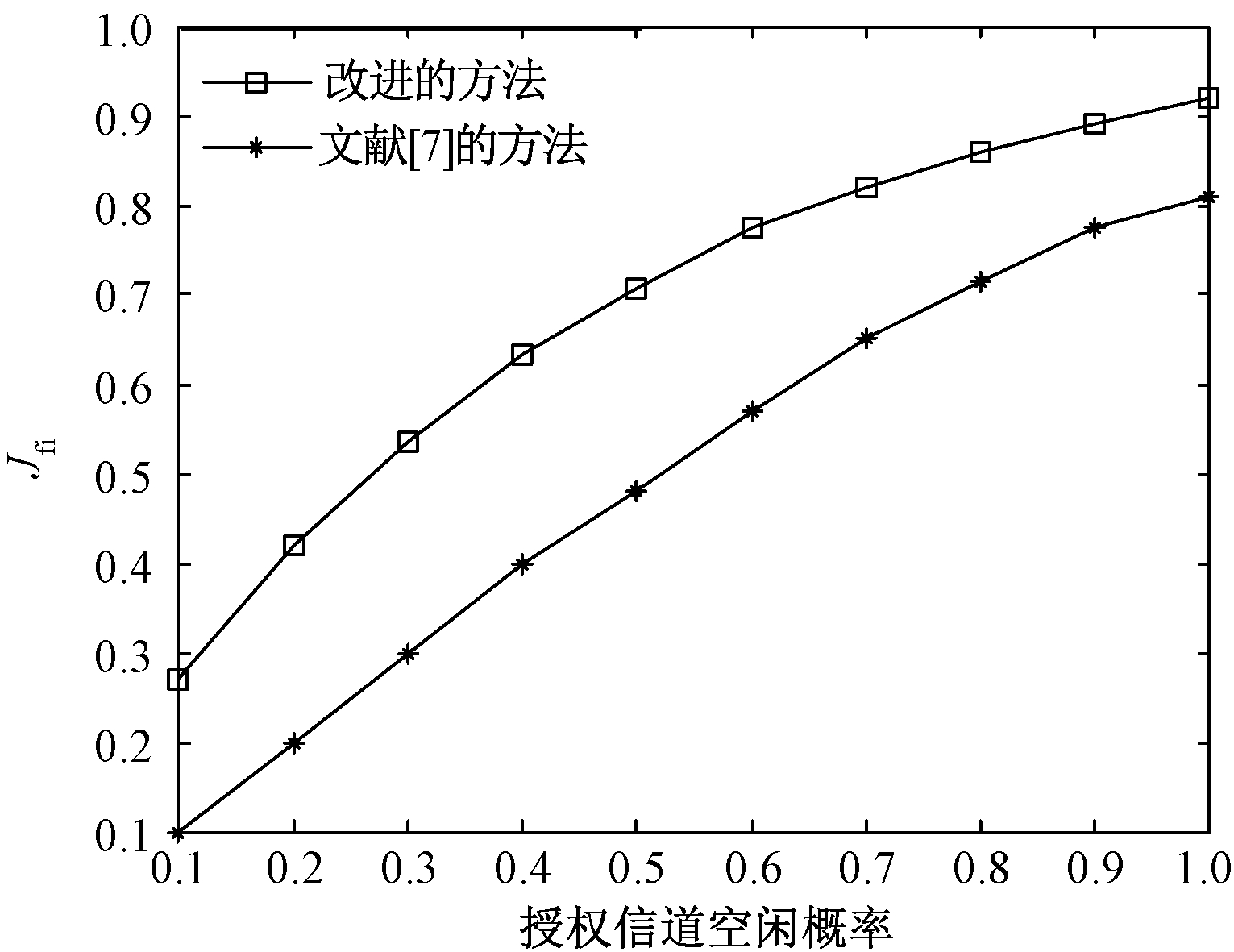
图5 Jain公平指数比较
Fig.5 Comparison of the Jain′s fairness index
4 结束语
笔者同时考虑认知用户需求和干扰两个因素，构建了干扰约束下基于用户需求的多信道机会频谱接入问题.以用户满意度减去干扰值为净收益函数，最大优化采用博弈论的方法，证明该博弈是至少具有一个纯策略纳什均衡的精确势能博弈，且纳什均衡点是上述优化问题的全局最优解.仿真结果证明了优化问题的合理性和有效性，表明考虑干扰因素后，可以显著降低整个网络的抗干扰水平，同时得到较高的用户满意度和更高的公平性，提升了系统总体性能.
[1] 穆晓敏,师光强,刘颖,等. 一种基于合约的认知网络协作频谱共享策略[J]. 郑州大学学报(工学版)，2016,37(3)：1-5.
[2] SAKIN S A, RAZZAQUE A. Game theoretic downlink resource scheduling for self-coexisting cognitive radio networks[C]//International Conference on Networking Systems and Security.Dhaka,Bangladesh：IEEE, 2016: 1-7.
[3] FUDENBERG D, TIROLE J. Game theory [M]. Cambridge, MA: MIT Press,1991．
[4] ACERO D O, EKICI E. Distributed multiple access in multichannel cognitive radio networks via potential games[C]//2015 13th International Symposium on Modeling and Optimization in Mobile, Ad Hoc, and Wireless Networks. Mumbai, India:IEEE,2015:123-130.
[5] XU Y H, WU Q H, SHEN L, et al. Opportunistic spectrum access with spatial reuse: graphical game and uncoupled learning solutions[J]. IEEE transactions on wireless communications,2013,12(10): 4814-4826.
[6] CHEN X, HUANG J W. Distributed spectrum access with spatial reuse[J]. IEEE journal on selected areas in communications, 2013, 31(3): 593-603.
[7] WU Q H, WU D C, XU Y H, et al. Demand-aware multichannel opportunistic spectrum access: a local interaction game approach with reduced information exchange[J]. IEEE transactions on vehicular technology. 2015, 64(10): 4899-4904.
[8] ZHANG Y H, YANG F, KAN C R, et al. QoE-aware distributed carrier aggregation in cognitive small cell networks: a game-theory approach[C]//2016 25th Wireless and Optical Communication Conference. Chengdu, China: IEEE, 2016:1-5.
[9] ZHANG N, ZHANG S, ZHENG J C, et al. User satisfaction-aware radio resource management in ultra-dense small cell networks[C]//2016 IEEE/CIC Internati-onal Conference on Communications in China. Chengdu, China: IEEE,2016:10-15.
[10] XU Y H, WANG J L, WU Q H, et al. Opportunistic spectrum access in cognitive radio networks: global optimization using local interaction games[J]. IEEE journal of selected topics in signal processing, 2012, 6(2): 180-194.
[11] GHOSH A, COTTATELLUCCI L, ALTMAN E. Normalized nash equilibrium for power allocation in cognitive radio networks [J]. IEEE transactions on cognitive communications and networking,2015,1(1)： 86-99.