0 引言
经济负荷分配问题(economic load dispatch problem,EDP)的目标是在满足各种等式与不等式约束的情况下减少总燃料成本.求解EDP的优化方法大体可以分为两类:传统的数值优化方法和智能优化方法.传统的优化方法包括线性规划、二次规划和内点法等[1-2].这类方法高效且精确,但对初始值很敏感,易提前收敛于局部最优解.智能优化方法包括遗传算法[3-4]、进化策略[5]、粒子群优化[6-7]和差分进化算法(differential evolution,DE)[8-9]等.此类方法对所求问题的特性没有要求,还能应用于复杂的大规模优化问题[10],因而被越来越多的学者所采用.为了提高效率和精度,这些算法往往经过了复杂的改进,例如有些算法[11]还需借助于二次序列规划的局部搜索能力,这些改进在很大程度上给使用者带来了麻烦.因此,笔者将采用最基本的差分进化算法[12]来求解该问题.
本文的重点在于约束处理方法.前面提到的方法大部分采用罚函数法,该方法需要设置罚系数,易造成过惩罚或欠惩罚的问题.智能优化算法中最常用的约束处理方法有可行性规则(feasi-bility rules,FR)[13]和ε约束法[14],这两种方法简单高效且易于与进化算法结合,因而得到了非常广泛的应用[15].但在EDP中,却鲜少发现这两种方法的存在.通过分析FR和ε 约束法的特性以及所求问题的特点,发现了这两种方法不适合求解EDP问题的原因.在此基础上,结合EDP问题的特点,笔者提出了一种将负荷平衡约束转化为边界不等式约束的方法,转化后在进化算法中采用FR和ε约束法便十分有效了.实验结果表明,即便采用最简单的差分进化算法,仍然能求得非常有竞争力的解.
1 EDP的数学模型
EDP的目标是在一定时间内在满足电力系统运行条件的情况下,通过对发电机组的发电功率进行优化使得系统的燃料成本最小.
电力系统燃料成本FC是每个发电机组燃料成本的总和,如式(1)所示:
(1)
式中:n为系统的发电机组数;pi为第i台发电机功率;FCi(pi)为第i个发电机组的燃料成本函数. FCi(pi)通常被拟合为一个二次多项式,如式(2)所示:
FCi(pi)=aipi2+bipi+ci, i=1,2,…,n,
(2)
式中:ai、bi、ci为燃料成本的系数.
考虑以下4个约束.
(1)功率平衡约束.在考虑系统损耗的情况下,电力系统的发电功率应等于实际功率需求D与系统的转运损耗PL之和,如式(3)所示:
(3)
系统的转运损耗由式(4)计算:
(4)
式中:Bij、Bi0、B00为损耗系数.
(2)电机发电功率范围约束.单个发电机组的发电功率pi必须满足最小与最大功率约束pimin、 pimax,即
pimin≤pi≤pimax, i=1,2,…,n.
(5)
(3)功率升降限制约束.考虑输出功率的升降限制,即较前一次的输出功率相比,当前的输出功率要在一定的范围之内.具体约束如下式所示:
![]()
(6)
式中:![]() 为前一次的输出功率;DRi为当前功率下降时下降范围的限度;URi为功率上升时上升范围的限度.
为前一次的输出功率;DRi为当前功率下降时下降范围的限度;URi为功率上升时上升范围的限度.
(4)禁止功率区域约束.某些发电机组有一些禁止功率区域.其约束如式(7)所示:
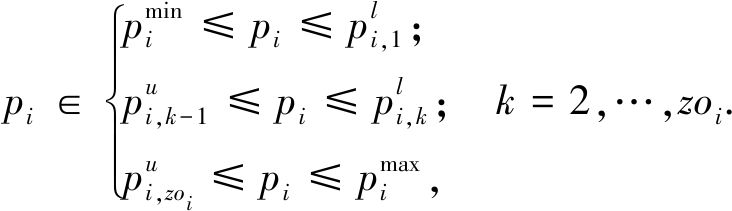
(7)
式中:![]() 和
和![]() 为发电机组i的第k个禁止区的下界和上界.
为发电机组i的第k个禁止区的下界和上界.
2 约束处理
当采用进化算法求解上述问题时,式(5)表示的电机发电功率范围约束通常被处理为自变量的边界约束.
数学模型中有4个约束,通常将发电机组功率范围约束和功率升降限制约束结合形成如下的自变量边界约束:
(8)
可对新解中的越界分量重新赋值来处理该约束.对于功率平衡约束和禁止功率区域约束,以往文献中通常采用罚函数法.除罚函数法以外,可行性规则(feasibility rules,FR)与ε 约束处理法是进化算法中两种常见的约束处理方法[15],都可以用来比较两个解的优劣.
FR最初用于遗传算法中的锦标赛选择,其具体表述如下:当两个解都不可行时,根据约束违反量的大小来比较优劣;当两个解一个可行、另一个不可行时,可行解优于不可行解;当两个解都是可行解时,根据目标函数的大小比较优劣.
ε 约束法最初由Takahama和Sakai[16]提出,与FR一样,ε 约束法也可用来比较两个解的优劣,只是在比较的时候增加了一个参数ε.比较规则如下:当两个解的约束违反量都大于ε 时,根据约束违反量的大小比较优劣;当两个解的约束违反量一个小于ε、另一个大于ε 时,前者优于后者;当两个解的约束违反量都小于ε 时,根据目标函数的大小来比较优劣.实际上,当ε=0时,ε 约束法就等同于FR.通常采用下式来控制ε 值[15]:
ε(0)=φ(Xθ);
(9)
式中:ε 的初值ε(0)被设为在初始种群中排第θ位的约束违反量φ(Xθ);t为当前迭代次数.当迭代次数t小于Tc时,ε 值按指数形式下降,下降速度由参数cp控制;否则的话,将ε 取值为0.
EDP中功率平衡等式约束会使得约束优化的可行域变为一个超平面.当问题的维度很大时,很难找到这个超平面上的可行解.另一方面,这个可行域超平面还很大,这意味着当偏好可行解的FR找到一个可行解后,就很难搜寻到远处的最优解了.ε 约束法能增加可行域的大小,在一定程度上能克服FR的缺点,但这种对可行域的扩增是暂时的,当ε 下降为0时,其本质上仍然是可行性规则,如果此时还没有找到超平面上邻近最优解的可行解,就很容易陷入超平面上的局部最小值.为了降低求解难度,通常的做法是将等式约束松弛为一个不等式约束,如式(10)所示.但这一方面难免影响到解的精确性,另一方面松弛为不等式约束后,可行域的范围还是很小.
(10)
式中:σ为一个很小的常数,如1e-3.
这里采用以下的改进方法处理功率平衡约束:采用DE来求解该问题时,只对前n-1个变量进行优化.在计算目标函数时,先根据功率平衡约束求解第n个未被优化的变量pn,并增加pn的两个边界约束,如式(11)所示,然后采用可行性规则或ε约束法来处理这两个约束:
(11)
功率平衡约束为一个二次式.对于二次式,可采用求解二次方程的方法来进行转换,将式(3)转化如下:
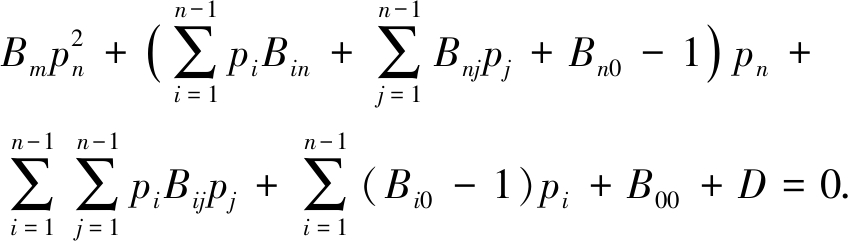
令![]()
则根据一元二次方程的求根公式可得:当b2-4ac≥0时,![]() 在这种情况下,b值通常接近
在这种情况下,b值通常接近![]() 因此,方程的两个根都是正值.但是两根中的较小值通常符合范围约束,而较大值却远远超出可行域的范围,因此,在这里取根为:
因此,方程的两个根都是正值.但是两根中的较小值通常符合范围约束,而较大值却远远超出可行域的范围,因此,在这里取根为:
(12)
但并不是所有的情况下,都满足b2-4ac≥0.尤其是在搜索过程的早期,通常b2-4ac<0,此时不能采用一元二次函数的求根公式求解pn值.因此,对式(3)进行简单变形,如下式所示:
(13)
此处采用了上次迭代中的pn值来计算PL,能够如此简化的原因是,相对于pn,PL的值较小,pn对PL的贡献值也很小,采用不精确的pn对PL的影响不大.通过上式可求得pn的近似值,也能很快搜寻到可行域附近.当搜寻到可行域附近后,易满足b2-4ac≥0的条件,然后就可根据式(12)求得满足功率平衡约束的可行解.
该约束处理方式的优势有三点:最重要的是将可行域极小的等式约束转化为了可行域较大的不等式约束,易找到可行解.其二,缩减了问题的一个维度,把n维的问题缩减到了n-1维.第三,不需要对等式约束进行松弛,能获得精确解.
对于功率禁止区域约束,如果pi位于第k个禁止区域中:![]() 采用式(14)计算其约束违反量的值.对每一项求和就可得到功率禁止区域约束的约束违反量值.
采用式(14)计算其约束违反量的值.对每一项求和就可得到功率禁止区域约束的约束违反量值.
(14)
3 实验结果与分析
3.1 约束差分进化算法
这里采用差分进化算法作为优化方法.差分进化算法(DE)最初由Storn & Price[12]在1997年提出,它具有简单、高效、参数少、易于编程实现等优点,DE是近年来得到关注最广泛的进化算法之一.它有4个基本步骤:初始化;变异;交叉;选择.根据变异策略及交叉方式的不同,DE算法有很多变种,这里采用最基本的DE/rand/1/exp.
结合可行性规则的DE的伪代码如图1所示.结合ε约束法的DE的伪代码与之类似.

图1 结合可行性规则的DE/rand/1/exp的伪代码
Fig.1 Pseudo code of DE/rand/1/exp with Feasibility rules
3.2 实例描述及参数设置
选用两个经典问题[7]来进行测试,将其分别命名为EDP1和EDP2.EDP1包含6个发电单元,26根总线和46根传输线,总功率需求是1 263 MW,6个单元的特性及损耗系数B值见文献[7].
EDP2包含15个发电单元,总功率需求是2 630 MW,15个单元的特性及B值见文献[7],约束差分进化算法参数设置如表1所示.
表1 算法参数设置
Tab.1 Parameter setting of algorithm
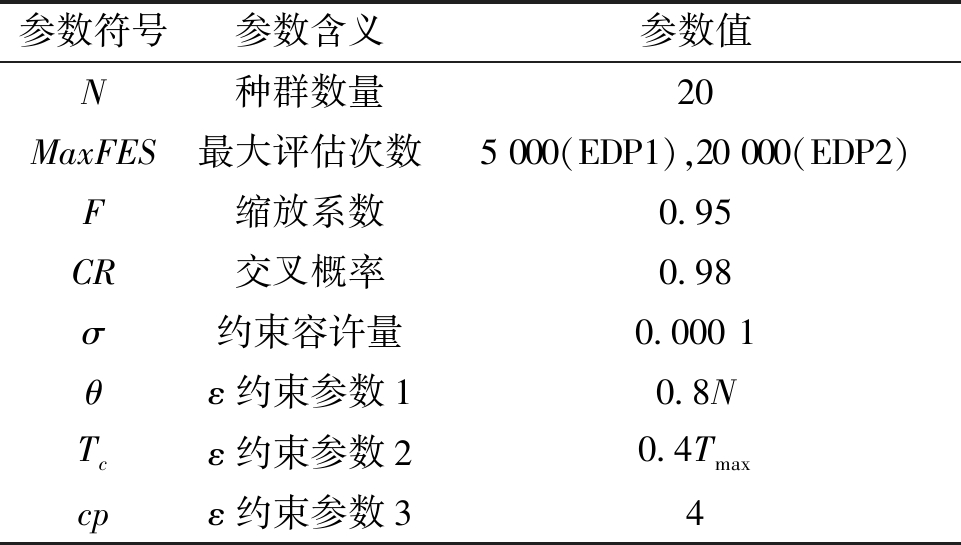
参数符号参数含义参数值N种群数量20MaxFES最大评估次数5 000(EDP1),20 000(EDP2)F缩放系数0.95CR交叉概率0.98σ约束容许量0.000 1θε约束参数10.8NTcε约束参数20.4Tmaxcpε约束参数34
3.3 实验结果
3.3.1 4种方案比较
将FR与DE结合并采用式(10)处理功率平衡约束称为方案1;将ε约束法与DE结合并采用式(10)处理功率平衡约束称为方案2;将FR与DE结合并采用改进方法处理功率平衡约束称为方案3;将ε约束法与DE结合并采用改进方法处理功率平衡约束求称为方案4.
4种方案在EDP1和EDP2上独立运行30次的统计结果如表2所示.从表2可见,对于EDP1和EDP2,方案3和方案4的结果明显优于方案1和方案2.对于EDP1,方案2的结果也明显优于方案1,可见对于该问题ε 约束法是有效的.方案3和方案4没有显著性差异,这是因为采用改进方法处理功率平衡约束后,算法的效率很高,方案3和方案4都能找到很好的解.对于EDP2,方案1的最优值和最差值要优于方案2,但方案2的平均值要优于方案1,而方案4的结果优于方案3,可见ε 约束法表现较好.
表2 4种方案在EDP1和EDP2上的统计结果
Tab.2 Statistical results for four tests on EDP1 and EDP2 美元

方案EDP1EDP2最优值平均值最差值标准差最优值平均值最差值标准差方案115 444.1315 465.4615 499.1217.402 232 955.3533 107.1833 239.6875.594 12方案215 444.1015 459.4615 493.8110.654 032 972.3833 079.7133 251.8275.081 19方案315 443.5715 443.5715 443.573.82E-0732 698.7932 705.1232 751.6114.841 84方案415 443.5715 443.5715 443.572.79E-0732 698.3832 700.1232 702.801.144 96
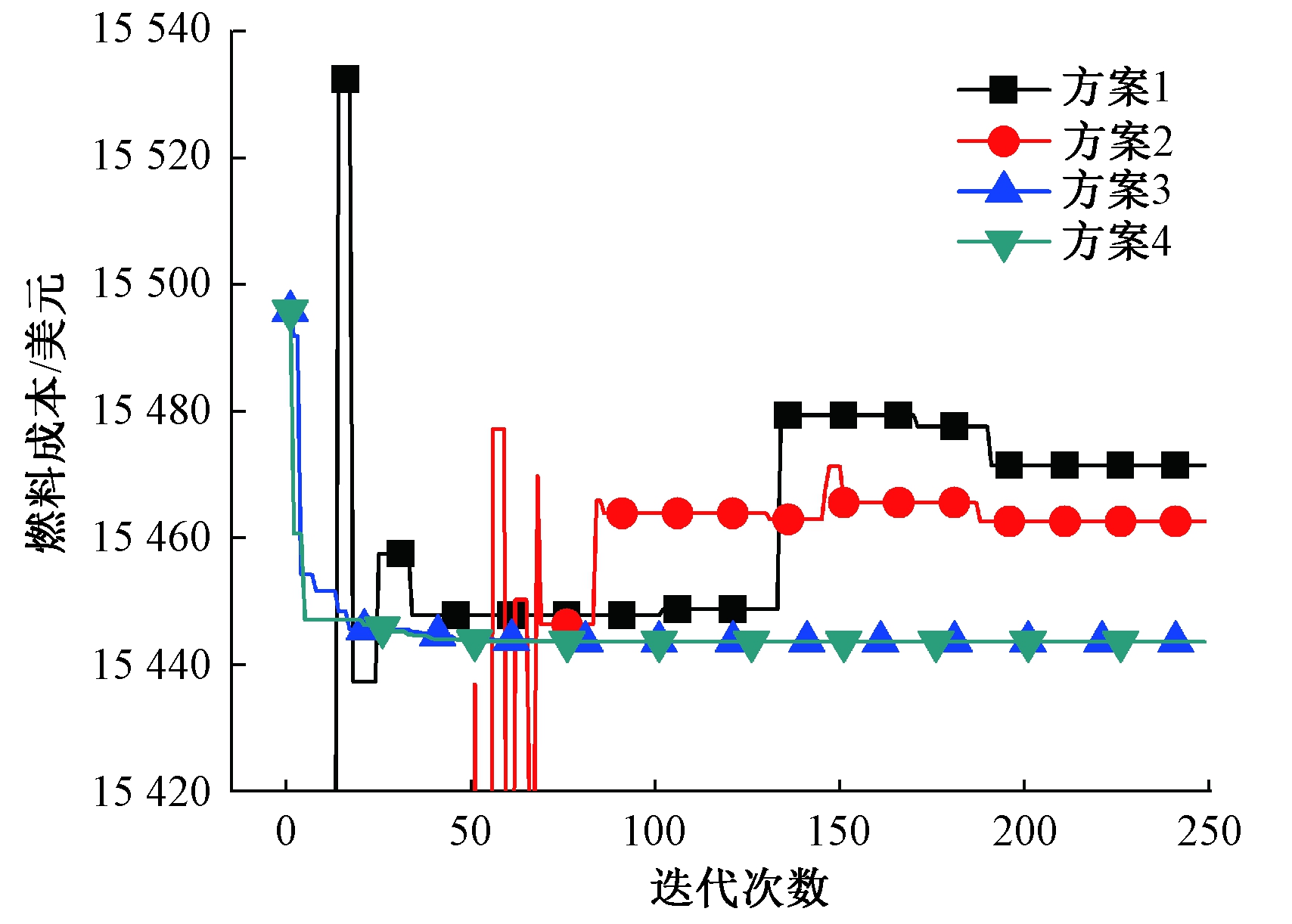
图2 4种方案在EDP1上目标函数的收敛图
Fig.2 Convergence plots of four tests on EDP1
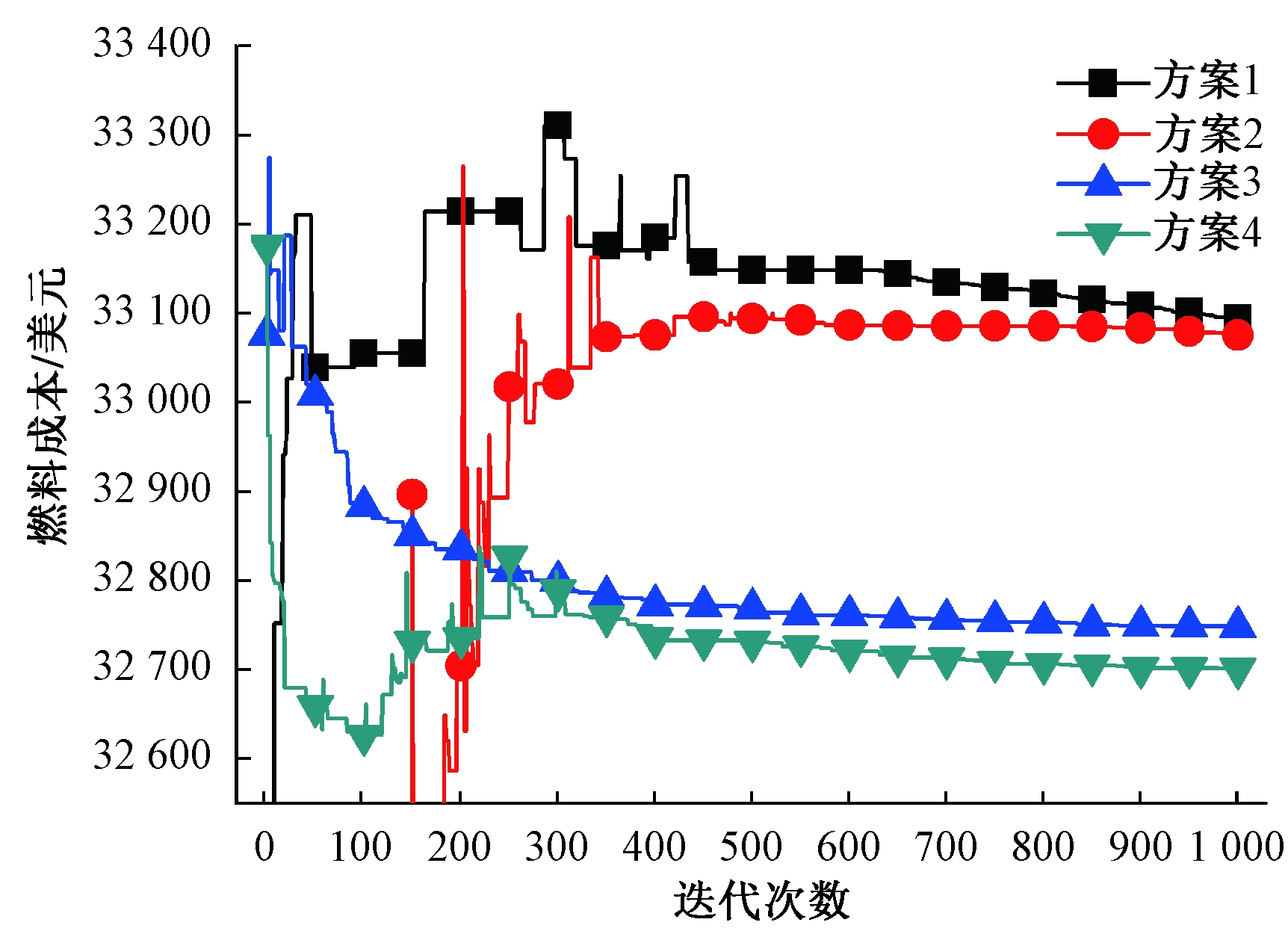
图3 4种方案在EDP2上目标函数的收敛图
Fig.3 Convergence plots of four tests on EDP2
4种方案在两个问题上的收敛过程如图2和图3所示.在搜索前期,方案1出现了目标函数值的波动,这是因为在可行性规则下,方案1力求找到可行解,只优化约束违反量.而方案2在ε约束的作用下,可以先优化目标函数,因而刚开始时方案2获得了很小的目标函数值,但随着ε 的减小,目标函数值越来越大;当ε快变为0时,收敛曲线在最优解附近停留了一段时间,但最终丢失了该解,陷入了局部最优.这是因为在功率平衡等式约束下,可行域太小,而可行性规则和ε 约束法偏好可行解,难以找到全局最优.而方案3和方案4,对唯一的等式约束进行了处理,使算法中的种群都是可行解,能直接优化目标函数.因此,方案3和方案4都极快地收敛到了全局最优解.
对于EDP2,方案1和方案2的表现与EDP1中类似.但因为该问题维度较高,方案1和方案2的解与方案3和方案4相差较大.方案3和方案4相比,很显然,ε 约束法在这里起了很大作用.方案4中,目标函数值先迅速下降,随着ε 的减小,略有上升,然后再缓慢下降.与方案2不同的是,方案4中的目标函数值变化比较缓慢,不至于丢失近优解.
3.3.2 与文献方法的比较
文献中有很多算法对该问题进行了求解,如模拟退火算法(simulated annealing,SA)[17]、遗传算法(genetic algorithm,GA)[6]、粒子群算法(particle swarm optimization,PSO)[6-7,18]、人工免疫系统(artificial immune system,AIS)[19].这些算法均采用罚函数方法来处理约束,并且大多在基础算法上进行了改进.
各种算法的统计结果如表3和表4所示.表中展示了各算法在多次运行下的最优值、平均值、最差值和标准差.某些算法的标准差未知,对于函数评估次数,PSO和GA均为20 000次;CPSO(chaotic particle swarm optimization)算法在文献[7]中未给出局部搜索的参数,但能推算出函数评估次数要大于14 400;对于SOH_PSO(self-organizing hierarchical particle swarm optimization)[18],在EDP2上的种群数量达到了400和500,即使其函数迭代次数只有125,其函数评估次数也分别为50 000和62 500,远超方案3和方案4在EDP2上的最大函数评估次数20 000.通过这些数据可知,方案3和方案4在EDP1和EDP2上的最大函数评估次数(分别为5 000和20 000)是比较少的.
表3 在EDP1上各算法的统计结果
Tab.3 Statistical results of some algorithms on EDP1 美元
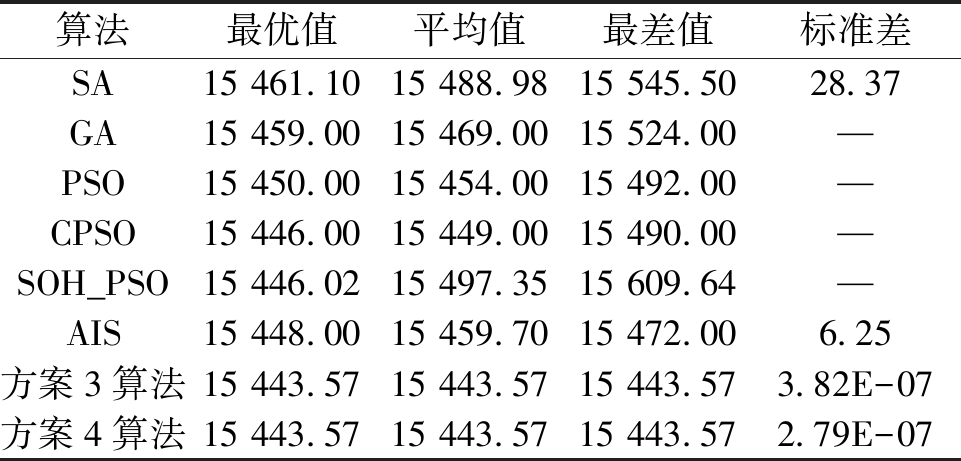
算法最优值平均值最差值标准差SA15 461.1015 488.9815 545.5028.37GA15 459.0015 469.0015 524.00—PSO15 450.0015 454.0015 492.00—CPSO15 446.0015 449.0015 490.00—SOH_PSO15 446.0215 497.3515 609.64—AIS15 448.0015 459.7015 472.006.25方案3算法15 443.5715 443.5715 443.573.82E-07方案4算法15 443.5715 443.5715 443.572.79E-07
表4 在EDP2上各算法的统计结果
Tab.4 Statistical results of some algorithms on EDP2 美元
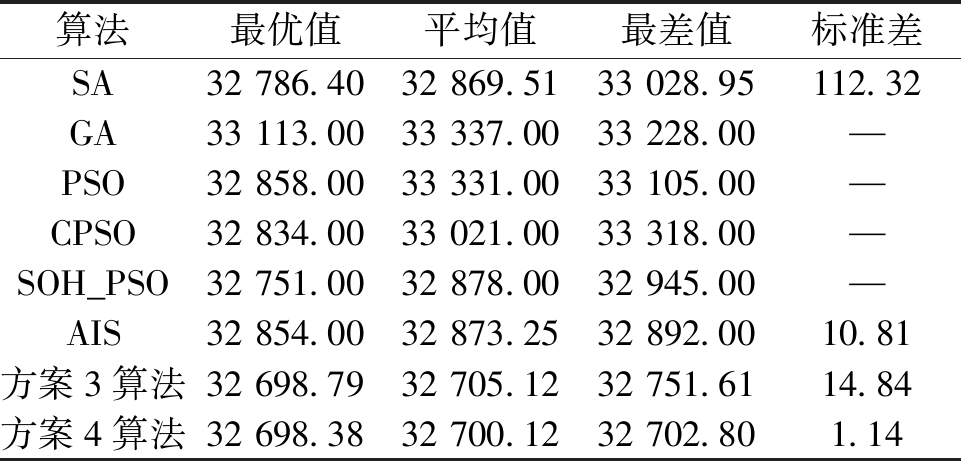
算法最优值平均值最差值标准差SA32 786.4032 869.5133 028.95112.32GA33 113.0033 337.0033 228.00—PSO32 858.0033 331.0033 105.00—CPSO32 834.0033 021.0033 318.00—SOH_PSO32 751.0032 878.0032 945.00—AIS32 854.0032 873.2532 892.0010.81方案3算法32 698.7932 705.1232 751.6114.84方案4算法32 698.3832 700.1232 702.801.14
从表3可见,对于EDP1,方案3和方案4的结果要全面优于所比较的算法.其原因就在于等式约束的存在,而采用罚函数的方法容易造成过惩罚,使算法偏好可行解,容易收敛到局部最优.
从表4可见,对于EDP2,方案4在所有指标中都是最优的;而方案3的结果也远优于其他算法.由此可见,对于维度较大的问题,采用罚函数法来处理约束的效果更差.采用改进方法处理功率平衡约束后,FR和ε 约束法均能求得较好的结果,特别是ε 约束法的效果更佳.
4 结语
可行性规则与ε 约束法是进化算法中两种常用的约束处理方法,在以往的文献中,虽然有很多的进化算法被用来求解EDP问题,但大部分约束处理方法都是传统的罚函数法.笔者分析了EDP问题中不适合采用可行性规则和ε 约束法的原因,并提出了一种将EDP中的功率平衡约束转换为不等式约束的方法.实验结果表明,采用该方法时,即便是采用最基本的差分进化算法,也能求得非常有竞争力的解.
[1] ADLER R B, FISCHL R. Security constrained economic dispatch with participation factors based on worst case bus load variations[J]. IEEE transactions on power apparatus and systems, 1977, 96(2): 347-356.
[2] IRISARRI G, KIMBALL L M, CLEMENTS K A, et al. Economic dispatch with network and ramping constraints via interior point methods[J]. IEEE transactions on power systems, 1998, 13(1): 236-242.
[3] LING S H, LEUNG F H F. An improved genetic algo-rithm with average-bound crossover and wavelet mutat-ion operations[J]. Soft computing,2007,11(1):7-31.
[4] 杨胡萍, 李威仁, 左士伟, 等. 基于改进遗传算法的电力系统无功优化[J]. 郑州大学学报(工学版),2015, 36(6): 66-69.
[5] PEREIRA-NETO A, UNSIHUAY C, SAAVEDRA O R. Efficient evolutionary strategy optimisation procedure to solve the nonconvex economic dispatch problem with generator constraints[J]. IEEE proceedings-gener-ation, transmission and distribution, 2005, 152(5): 653-660.
[6] GAING Z L. Particle swarm optimization to solving the economic dispatch considering the generator constraints[J]. IEEE transactions on power systems, 2003, 18(3): 1187-1195.
[7] CAI J J, MA X Q, LI L X, et al. Chaotic particle swarm optimization for economic dispatch considering the generator constraints[J]. Energy conversion and management, 2007, 48(2): 645-653.
[8] COELHO L S, MARIANI V C. Combining of chaotic differential evolution and quadratic programming for economic dispatch optimization with valve-point effect[J]. IEEE transactions on power systems, 2006, 21(2): 989 - 996.
[9] 吴亮红, 王耀南, 袁小芳, 等. 基于快速自适应差分进化算法的电力系统经济负荷分配[J]. 控制与决策, 2013, 28(4): 557-562.
[10] 梁静, 刘睿, 瞿博阳, 等. 进化算法在大规模优化问题中的应用综述[J]. 郑州大学学报(工学版), 2018, 39(3): 15-21.
[11] VICTOIRE T A A, JEYAKUMAR A E. Hybrid PSO-SQP for economic dispatch with valve-point effect[J]. Electric power systems research, 2004,71(1): 51-59.
[12] STORN R, PRICE K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. J Global Optim, 1997, 11(4): 341-359.
[13] DEB K. An efficient constraint handling method for genetic algorithms[J]. Computer methods in applied mechanics and engineering, 2000, 186(2/4): 311-338.
[14] TAKAHAMA T, SAKAI S. Constrained optimization by the ε constrained differential evolution with grad-ient-based mutation and feasible elites[C]//2006 IEEE International Conference on Evolutionary Computation (CEC). Vancouver, BC: IEEE, 2006: 1-8.
[15] MEZURA-MONTES E, COELLO C A C. Constraint-handling in nature-inspired numerical optimization: past, present and future[J]. Swarm and evolutionary computation, 2011, 1(4): 173-194.
[16] TAKAHAMA T, SAKAI S, IWANE N. Constrained optimization by the ε constrained hybrid algorithm of particle swarm optimization and genetic algorithm[C]//Proceeding of AI 2005: Advances in Artificial Intelligence. Berlin: Springer, 2005: 389-400.
[17] POTHIYA S, NGAMROO I, KONGPRAWECHNON W. Application of multiple tabu search algorithm to solve dynamic economic dispatch considering generator constraints[J]. Energy conversion and management, 2008, 49(4): 506-516.
[18] CHATURVEDI K T, PANDIT M, SRIVASTAVA L. Self-organizing hierarchical particle swarm optimization for nonconvex economic dispatch[J]. IEEE transa-ctions on power systems, 2008, 23(3): 1079-1087.
[19] PANIGRAHI B K, YADAV S R, AGRAWAL S, et al. A clonal algorithm to solve economic load dispatch[J].Electric power systems research,2007, 77(10): 1381-1389.