0 引言
无轴承电机是随着电子技术、数字信号处理技术和控制技术发展而来的一种新型电机[1],是将电机的旋转和悬浮支承功能集成于一体[2],并具有磁悬浮轴承无接触、无摩擦和转速高等优点[3-4].但是传统永磁型无轴承电机径向悬浮力和转矩相互制约,从而导致承载力和刚度较小,制约了传统无轴承电机的发展和应用[5].
洛伦兹力无轴承电机是一种新型无轴承电机,它的转矩和轴向悬浮力都是由洛伦兹力产生的,定子绕组是一套单层绕组线圈,而转子结构类似于普通交替极永磁体电机,永磁体在转子铁心两端沿径向排列,并且沿转子铁心两端排列的永磁体极性不同,转子的径向支承依靠径向永磁轴承实现,永磁轴承不但使结构紧凑,并且几乎无能耗.由于无需引入额外的机械支承,从而减小了洛伦兹力无轴承电机的轴向尺寸,因此在对电机性能要求较高的领域具有广阔的应用前景,如生命科学领域、半导体工业和化工领域等.洛伦兹力无轴承电机在运行时,转子轴向偏移会使径向永磁轴承产生轴向力,因此轴向平衡是依靠永磁轴承产生的轴向力和无轴承电机产生的轴向洛伦兹力维持,所以洛伦兹力无轴承电机对轴向洛伦兹力控制精度要求更高,这也是一个难点.
文献[6]中设计了一款新型无轴承电机,建立了悬浮力和电流的数学模型,再通过对无轴承电机结构的有限元仿真分析得到悬浮力分布特性,并通过试验验证了建立的数学模型的准确性.文献[7]中设计了定子无齿槽结构的无轴承电机,通过有限元软件对无轴承电机结构进行分析,得到了磁场和悬浮力的分布特性.文献[8]提出采用不同永磁体组成多种转子结构,再通过有限元法分析建立的结构模型,得出电机转子的气隙磁通密度分布特性,从而计算得到电机的悬浮力和转矩,并对样机进行实验,验证了通过有限元法分析得到的结果的准确性.
以上文献的研究主要是针对无轴承电机的结构设计及其转子径向悬浮力的优化分析,并未涉及转子的轴向受力分析.笔者提出的基于洛伦兹力的无轴承电机能同时产生转矩和轴向悬浮力,然后针对设计的无轴承电机,研究其悬浮原理,建立轴向洛伦兹力的数学模型,对转子永磁体进行优化设计,采用有限元法对轴向洛伦兹力分布特性进行研究,通过与理论计算结果进行比较,验证设计方案的可行性.
1 洛伦兹力无轴承电机
1.1 洛伦兹力无轴承电机原理
笔者设计的洛伦兹力无轴承电机,其定子铁心内表面是无齿槽结构,其中A相绕组由A11和A12串联组成,B相和C相绕组构成与A相类似.多相绕组为多匝漆包线构成的单层绕组,再用胶固化和定位,多相绕组均布在定子铁心内表面.转子铁心上为交错极永磁体,定、转子结构如图1所示.
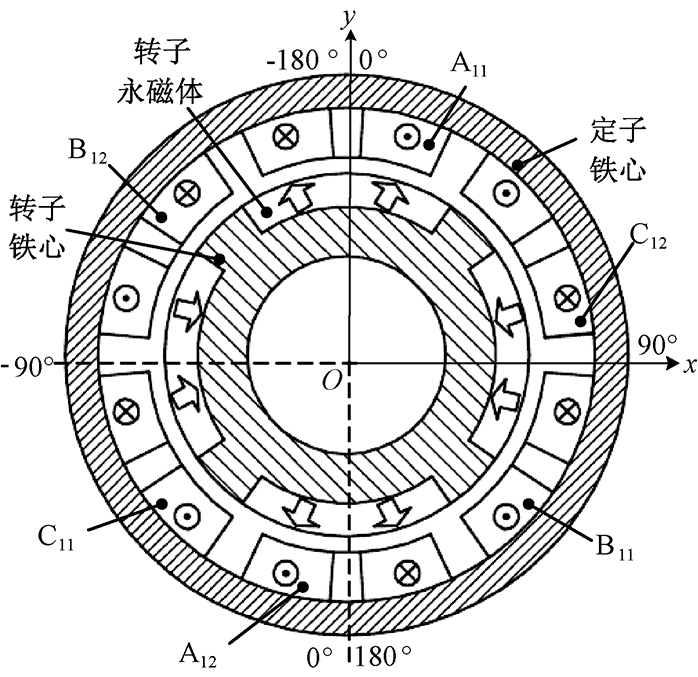
图1 定子和转子结构
Fig.1 Structure of stator and rotor
基于洛伦兹力的无轴承电机的主要功能实现部件如图2所示,图2中1和8为一对径向永磁轴承,为转子提供径向悬浮力Fr,并且可以产生辅助轴向支承的轴向力Fz;2和6为长度不相等的转子永磁体,径向充磁,且极性相反,为无轴承电机产生工作磁场;3和5为定子绕组末端,产生轴向洛伦兹力FL;4为定子绕组中部,产生切向洛伦兹力,进而转化为转矩,只需在定子绕组中通入悬浮电流和转矩电流,通过控制算法解耦即可实现同时产生独立的轴向悬浮力和转矩;7为转子铁心,上面安装固定转子永磁体.
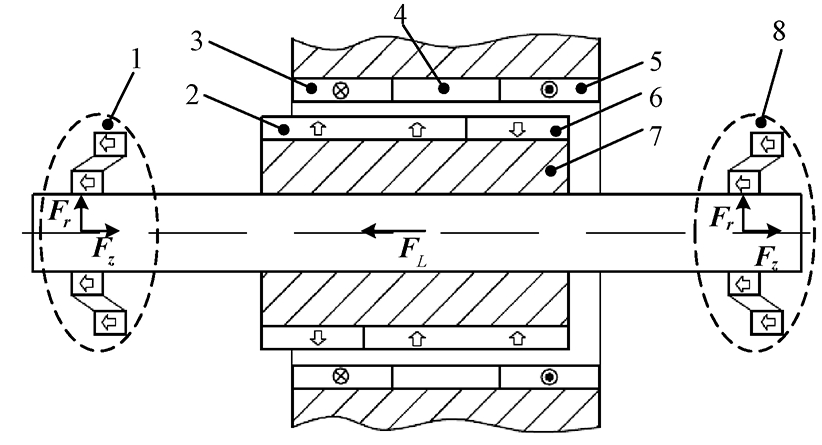
图2 无轴承电机的功能部件
Fig.2 Function units of bearingless motor
1.2 洛伦兹力无轴承电机结构
笔者研究的洛伦兹力无轴承电机的三维模型如图3所示,二维结构简图如图4所示.无轴承电机转子磁极对数P=2,转子的轴向位置检测通过电涡流位移传感器实现,转子圆周位置检测由霍尔传感器实现.
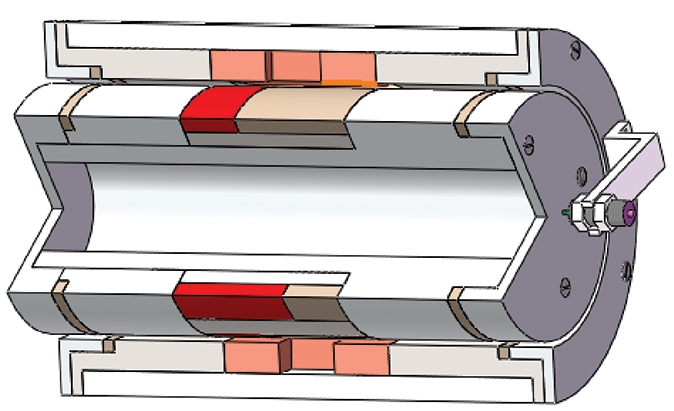
图3 无轴承电机三维模型
Fig.3 3D model of bearingless motor
转子磁极由长、短两种永磁体交错排列组成,沿转子铁心交错排列,且充磁方向相反.
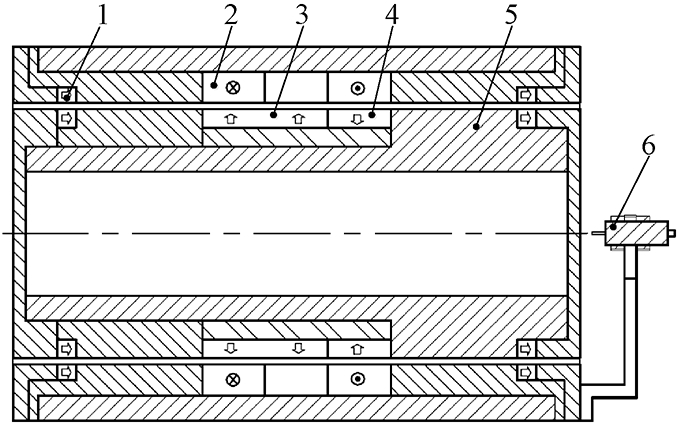
1.径向永磁轴承;2.定子绕组;3.长永磁体;4.短永磁体;5.转轴;6.电涡流位移传感器
图4 无轴承电机结构图
Fig.4 Structure diagram of bearingless motor
2 无轴承电机的设计
2.1 转子径向支承的设计
径向永磁轴承结构简图如图5所示,根据Earnshaw定理,永磁轴承的刚度满足:
2sr+sz=0,
(1)
式中:sr为永磁轴承径向刚度;sz为永磁轴承轴向刚度.
设永磁轴承的动磁环的轴向偏移量为dz,轴向承载力为Fz,于是有:
Fz=sz·dz,
(2)
式中:dz为动磁环轴向偏移量.
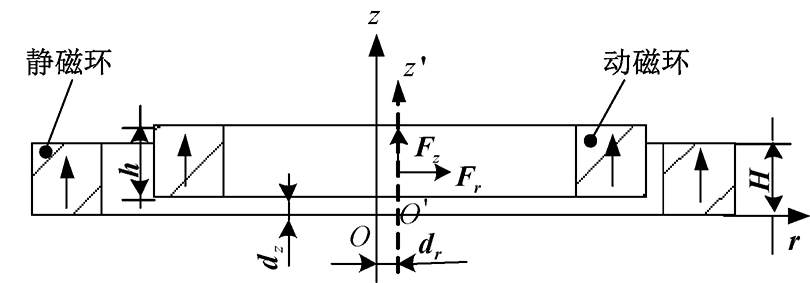
图5 径向永磁轴承结构图
Fig.5 Structure diagram of radial PMB
径向永磁轴承的动磁环安装在转子铁心上,可以通过电涡流位移传感器检测得到转子的轴向位移,在已知永磁轴承轴向刚度时,即可得到永磁轴承的轴向悬浮力.
径向永磁轴承的磁环采用轴向充磁,无轴承电机的径向永磁轴承磁环主要结构参数见表1.
表1 径向永磁轴承磁环结构参数
Tab.1 Structural parameters of magnetic ring for radial PMB

参数数值动磁环内径/mm34动磁环外径/mm40静磁环内径/mm42静磁环外径/mm48磁环轴向厚度/mm2
2.2 转子的结构设计
洛伦兹力无轴承电机转子上的永磁材料选用稀土钕铁硼,牌号为N35,径向充磁,矫顽力为890 kA/m,剩磁强度为1.1 T,相对磁导率为1.05[9].对于内转子电机,其永磁体安装示意图如图6所示.参照文献[10]建立的轴向洛伦兹力数学模型.

图6 电机磁场计算模型
Fig.6 The analytical model of magnetic field for motor
设转子永磁体的磁势为Fm,则有:
(3)
式中:B为永磁体剩磁强度;μ0为真空磁导率; μ为永磁体相对磁导率;t为永磁体径向厚度.
设永磁体的磁阻为RM,气隙磁阻为Rδ,根据磁路欧姆定律,则有:
(4)
式中:P为无轴承电机极对数;α为电机的极弧系数;Rc为永磁体内半径;Rm为永磁体外半径;l为永磁体轴向长度.
(5)
式中:Rs为定子铁心内半径.
设气隙磁通量为Φδ,则有:
(6)
半径为R处绕组的磁通密度为B(R),则有:
(7)
式中:R为绕组处圆周半径,且Rm<R<Rs.
无轴承电机相关结构体参数见表2.
表2 无轴承电机结构参数
Tab.2 Structural parameters of bearingless motor
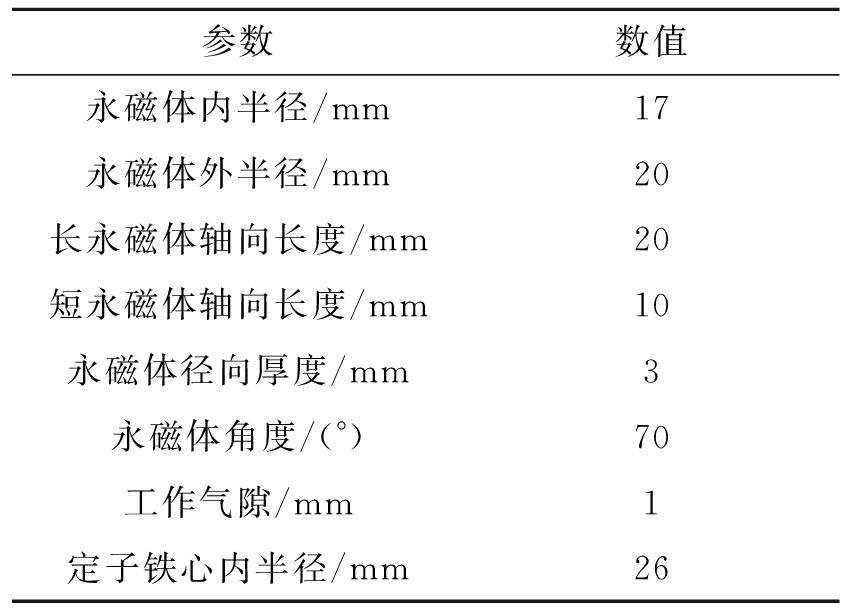
参数数值永磁体内半径/mm17永磁体外半径/mm20长永磁体轴向长度/mm20短永磁体轴向长度/mm10永磁体径向厚度/mm3永磁体角度/(°)70工作气隙/mm1定子铁心内半径/mm26
设无轴承电机的极距为τ,则有:
(8)
设转子永磁体宽度为cm,则有:
(9)
极弧系数为α,则有:
(10)
定子绕组中通入悬浮电流后,转子将受到洛伦兹力的作用,如图7所示.图7中la和lc为绕组末端和转子永磁体对应区域,产生大小相等和方向相同的轴向洛伦兹力.
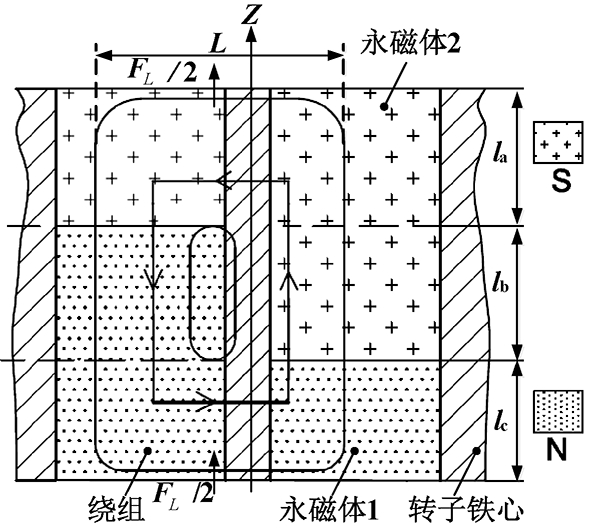
图7 无轴承电机轴向洛伦兹力
Fig.7 The axial lorentz force of bearingless motor
设单个绕组产生轴向洛伦兹力为FL,则有:
FL=2NB(R)ILα,
(11)
式中:N为单个绕组匝数;I为绕组中电流大小;L为绕组产生轴向洛伦兹力的长度.
要实现转子轴向平衡,故所受轴向洛伦兹力和永磁轴承的轴向悬浮力相等,即:
(12)
式中:n表示导通绕组的个数.
3 无轴承电机的支承分析
3.1 径向永磁轴承的有限元分析
有限元法可以有效地计算无轴承电机的相关性能参数,在ANSYS Workbench中建立永磁轴承的结构模型,对其动磁环处于不同的位置进行仿真分析.当磁环轴向厚度h从1.5 mm增大到3.5 mm时,不同径向位置时动磁环所受径向力Fr如图8所示.当动磁环轴向位移为0,径向偏移dr为0.5 mm,磁环轴向厚度H=h=2 mm时,最大径向力Fr为6.5 N.转子的总质量大约为0.3 kg,稳定运行时径向仅需克服转子重力,在最大径向位移时,一对永磁轴承产生的径向力可达到13 N.
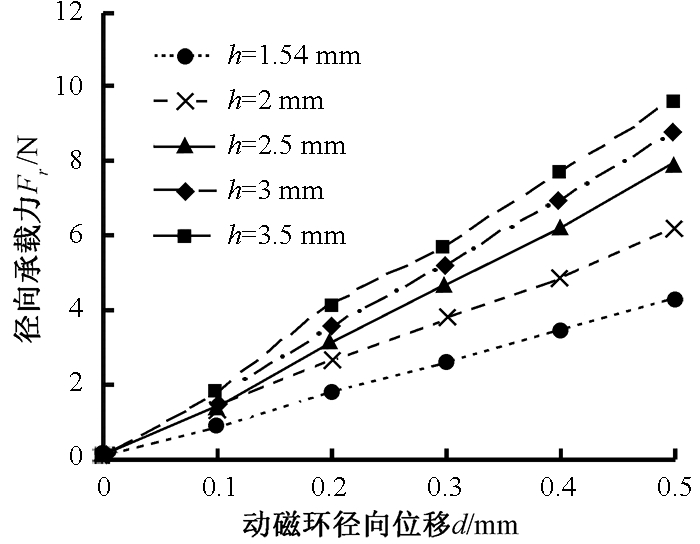
图8 不同磁环厚度下永磁轴承径向力
Fig.8 The radial force of PMB at different thickness of magnetic ring
当磁环轴向厚度h从1.5 mm增大到3.5 mm时,不同轴向位置时动磁环所受轴向力Fz如图9所示.当动磁环径向位移为0,轴向偏移dz为0.5 mm,磁环轴向厚度H=h=2 mm时,最大轴向力为Fz=10.5 N.因此,转子发生了轴向偏移,径向永磁轴承将会产生轴向力.因此要实现转子的轴向稳定,无轴承电机产生的轴向洛伦兹力FL和永磁轴承产生的轴向力Fz要平衡.
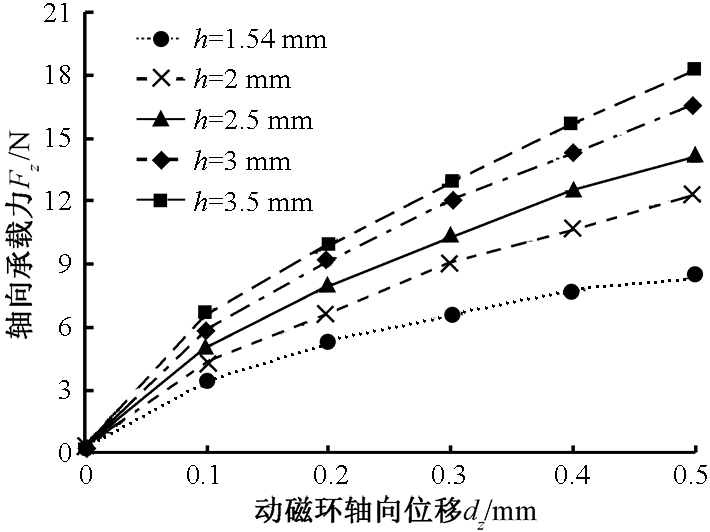
图9 不同磁环厚度下永磁轴承轴向力
Fig.9 The axial force of PMB at different thickness of magnetic ring
3.2 无轴承电机气隙磁场和轴向洛伦兹力
无轴承电机定子绕组上未加载电流时,转子永磁体产生的气隙磁场如图10所示.由图10可以看出,转子上永磁体安装位置处的磁场较强,最大磁场强度出现在转子铁心和永磁体交界处.

图10 转子永磁体磁场
Fig.10 The magnetic field of rotor permanent magnet
永磁体径向厚度t和气隙长度g对绕组所在区域的磁感应强度影响如图11所示.无轴承电机是一个对称结构,所以圆周位置的磁场分布沿轴线也是高度对称的,故在图1所示的[-180°,0°]和[0°,180°]范围内,磁场分布规律相同,为简化研究对象,所以选圆周角度[0°,180°]的区域为分析对象.
如图11(a)所示,在气隙长度g一定时,随着永磁体径向厚度t从2 mm增大到4 mm时,在绕组中点圆周径向位置,磁感应强度明显增大,但是对应的最大磁感应强度仅从0.22 T增大到0.35 T,但是并未呈倍数增加,这可能与磁饱和相关.如图11(b)所示,在永磁体厚度t一定时,随着单边气隙从1.5 mm减小到0.5 mm,最大磁感应强度从0.28 T增大到0.34 T.
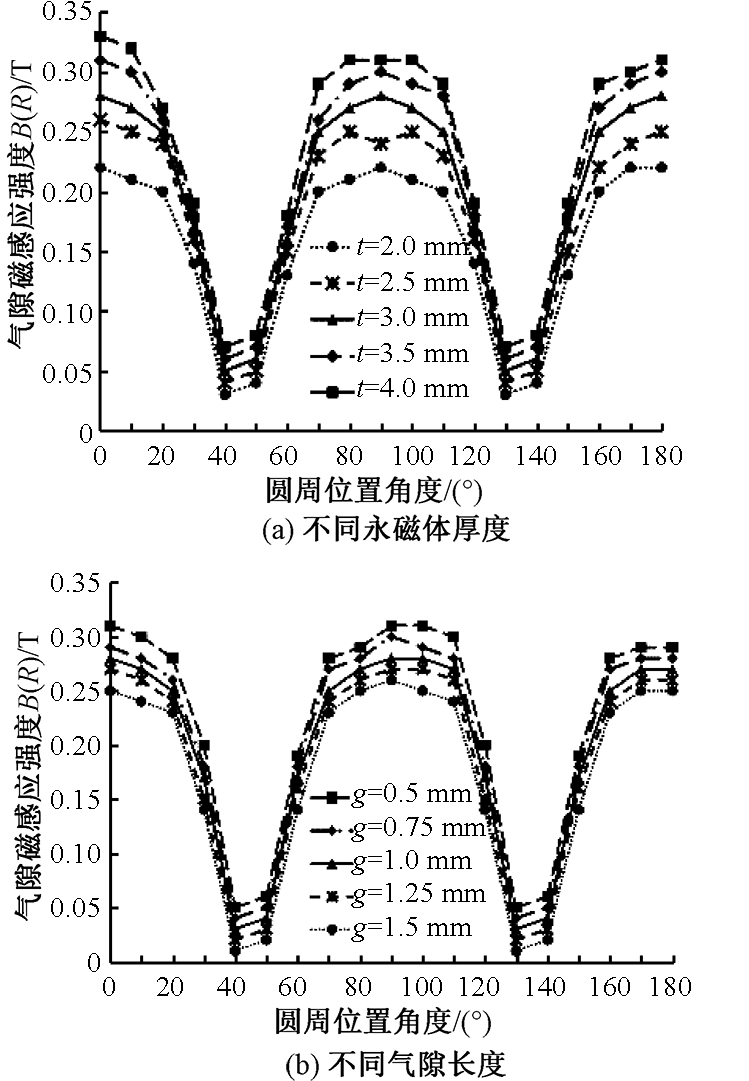
图11 不同永磁体厚度和气隙长度下磁感应强度
Fig.11 The magnetic flux density at different thickness of permanent magnet and gap
永磁体径向厚度t和气隙长度g对绕组产生的轴向洛伦兹力影响如图12所示.
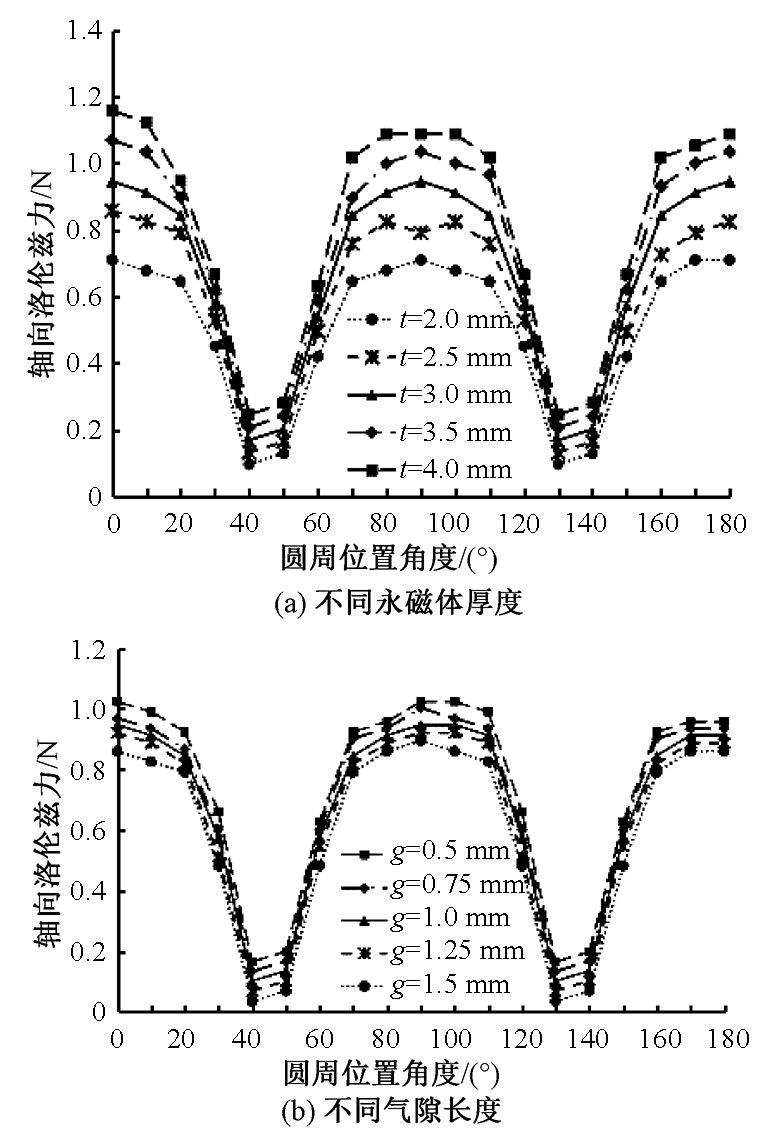
图12 不同永磁体厚度和气隙长度下轴向洛伦兹力
Fig.12 The axial lorentz force at different thickness of permanent magnet and gap
在绕组中通入的电流为1 A时,匝数为150,由图12(a)所示,在气隙长度g一定时,随着永磁体径向厚度t从2 mm增大到4 mm时,绕组的悬浮力从0.7 N增大到1.1 N,永磁体厚度增大,无轴承电机的轴向洛伦兹力明显变大,电机的轴向承载性能变强.如图12(b)所示,在永磁体厚度t一定时,随着单边气隙长度从1.5 mm减小到0.5 mm,单个绕组的最大悬浮力从0.9 N增大到1.1 N.
永磁体厚度t和气隙长度g主要通过改变绕组所在区域的磁感应强度影响轴向洛伦兹力的大小,其中永磁体厚度t增大,轴向洛伦兹力增大;气隙长度g减小,轴向洛伦兹力增大.综合考虑,选取永磁体径向厚度t=3 mm,气隙长度 g=1 mm.
3.3 洛伦兹力无轴承电机转子的轴向力
设计的无轴承电机绕组匝数N=150,在不同电流下,建立的数学模型和有限元仿真得到结果如图13所示.
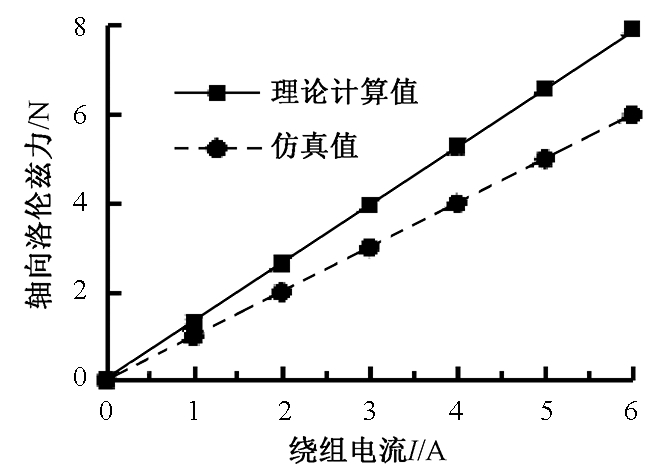
图13 单个绕组的轴向洛伦兹力
Fig.13 The axial lorentz force of single winding
有限元仿真显示,当绕组电流为1 A时,单个绕组产生的轴向洛伦兹力为0.94 N.对于理论计算模型,选择定子绕组区域径向圆周中点位置,此时圆周半径R=23.5 mm,由建立的数学模型知磁感应强度B=0.31 T,在安匝数NI为150 A时,轴向洛伦兹力为1.05 N,理论值与仿真值相差11.7%,由于采用ANSYS有限元软件分析时,软件计算考虑了漏磁情况而理论计算忽略了漏磁情况,所以软件仿真值较理论计算值小,但仿真结果表明设计的结构可满足工作要求,因此误差在可接受范围内.
有限元仿真结果显示,当绕组中电流为6 A时,单个绕组产生的轴向洛伦兹力为5.95 N.因此绕组选取合适大小的电流和导通方式,当选择三相两通六状态的导通方式,则4个绕组线圈产生的轴向洛伦兹力最大值可达23.8 N,转子所受的轴向洛伦兹力就可以平衡永磁轴承动磁环轴向偏移时产生的轴向力,足以将转子恢复到平衡位置.
4 结论
(1)根据磁路的欧姆定律,推导轴向洛伦兹力数学模型,并通过有限元法仿真了轴向洛伦兹力的分布特征,数学模型和有限元法分析均表明,永磁体厚度t增大,无轴承电机轴向洛伦兹力变大,电机的承载能力增强,最终选择永磁体厚度 t为3 mm.
(2)当设计的无轴承电机匝数为150时,通入的悬浮电流为6 A,如果选取导通三相绕组中的两相绕组,产生的最大轴向洛伦兹力可达23.8 N,即使转子处于最大轴向位移处时,无轴承电机产生的轴向力也足以让电机转子平衡,径向永磁轴承亦可满足无轴承电机转子的径向支承的要求.
参考文献:
[1] 解超,王晓琳,邓智泉,等.无轴承交替极电机控制系统改进及实现[J]. 中国电机工程学报, 2010,30(18): 78-84.
[2] 刘奕辰,朱熀秋.无轴承无刷直流电机研究现状及发展趋势[J]. 微电机, 2014,47(8): 74-78.
[3] 张维煜, 朱熀秋, 袁野. 磁悬浮轴承应用发展及关键技术综述[J]. 电工技术学报, 2015, 30(12): 12-20.
[4] SCHWEITZER G.磁悬浮轴承:理论、设计及旋转机械应用[M]. 北京:机械工业出版社,2012.
[5] 李炳楠,黄进.多相单绕组永磁无轴承电机的设计与运行分析[J].大电机技术,2012(5): 1-4.
[6] LEE H I, YOO S Y, NOH M D. Toroidally-wound self-bearing BLDC motor with lorentz force[J]. IEEE transactions on magnetics, 2010, 46(6): 2148-2151.
[7] BAUER W, AMRHEIN W. Electrical design considerations for a bearingless axial-force/torque motor[J]. IEEE transactions on industry applications, 2014, 50(4): 2512-2522.
[8] ZHU H, LI F. Optimization design of bearingless permanent-magnet slice motor [J]. IEEE transactions on applied superconductivity, 2016, 26(4): 1-4.
[9] 周寿增.烧结钕铁硼稀土永磁材料与技术[M]. 北京:冶金工业出版社, 2011.
[10] BAUER W, AMRHEIN W. Design and sizing relations for a novel bearingless motor concept[C]// International Conference on Electrical Machines and Systems. Beijing:IEEE Press, 2011: 1-6.