0 引言
模态固有频率和阻尼比是两个重要的模态参数,可为结构设计与优化、仿真计算与分析、载荷辨识与应用、故障检测与诊断等提供重要参考,因此,结构模态参数辨识在机械振动领域有其重要意义.长期以来,模态参数尤其是阻尼比的辨识由于难度大,重复性差等特点,一直是人们研究的热点问题.
模态参数辨识方法可分为时域法、频域法和时频法三种.最有代表性的时域法是对数衰减法[1],时域法往往只能处理平稳信号,并且对噪声的干扰比较敏感,且不适用于多模态参数辨识的情况.最常用的频域法是半功率带宽法[2],频域法建立在傅立叶变换的基础之上,能进行多模态参数的辨识,但其受采样频率、频率分辨率、采样分析点数等因素的影响.实际工程中的振动信号一般为非线性非平稳信号,时域法和频域法均不能处理非线性非平稳信号,要处理这种非线性非平稳信号,需采用时频法.时频法是一种新兴起的模态参数辨识方法,典型的时频法有短时傅立叶变换(STFT)[3]、小波变换(WT)[4]、经验模态分解(EMD)[5]、局部均值分解(LMD)[6]和本征时间尺度分解(ITD)[7]等.
STFT又称窗口傅立叶变换,其固定的时窗宽度使得时频分辨率也是固定的,即短时傅立叶变换的频率分辨率和时域分辨率相互影响,频率分辨率高则时域分辨率低,反之亦然[8].WT对信号的局部缺乏自适应性,在变换中小波基的选择对分析结果的影响很大[9].EMD可以对信号进行自适应分解,但是存在过包络、欠包络、模态混叠和端点效应等问题[10].付春等[11]提出了基于改进EMD-ICA的结构模态参数识别方法,并进行了仿真分析与试验验证.从仿真分析结果来看,EMD-ICA法识别模态频率与理论值最大误差为6%,识别的阻尼比最大误差大于23%.LMD是另一种自适应时频分析方法,其在抑制模态混叠和端点效应上优于经验模态分解,但是其主要问题是计算量较大[12].程军圣等[13]将LMD用于模态参数识别,对仿真信号和裂纹梁的测频信号进行了分析.从其研究结果来看,第3阶模态PF幅值自然对数和瞬时频率的拟合曲线效果不好,仿真分析中LMD法识别的模态频率与理论值相比最大误差大于5%,识别的阻尼比最大误差大于17%.ITD虽然仍然受到端点效应的影响,但是其在计算速度上相比较于经验模态分解和局部均值分解有明显优势,亦可用于实时处理大量数据[14].
鉴于此,笔者提出了一种基于IITD(经端点延拓改进的ITD)的模态参数辨识方法,并进行了仿真分析与试验验证,以验证模态参数辨识方法在结构模态参数辨识上有效性和实用性.
1 基于端点延拓的IITD法
1.1 ITD法
本征时间尺度分解(intrinsic time-scale decomposition,ITD)是Frei等[7]提出的一种处理非线性和非平稳信号的非参数算法.ITD法的优势在于它不需要原始信号序列的参数函数形式,ITD法将一非线性非平稳信号表征成一组固有旋转分量和一个趋势项之和.对于给定的非线性时间序列Xt, t∈(1,2,…,T),ITD法将信号分解成一系列频率依次降低的固有旋转分量(PR分量):
Xt=HXt+LXt=HXt+(H+L)LXt=
![]()
(1)
式中:H为固有旋转分量提取算子;L为基线提取算子.
ITD法将时间序列Xt分解成PR分量的步骤如下.
(1)确定信号Xt的所有极值点位置,并将其对应时刻标记为τk,k∈{1,2,…}.
(2)假设在t∈[0,τk+2]上Xt有离散数据点,在连续的极值点之间使用分段式线性基线提取算子L计算基线信号Lt如下:
t∈(τk,τk+1].
(2)
其中,Xk和Lk分别表示X(τk)和L(τk),且有
(1-α)Xk+1, 0<α<1.
(3)
(3)使用PR分量提取算子H可以得到Xt的第一个PR分量:
HXt=(1-L)Xt=Ht=Xt-Lt.
(4)
(4)将基线信号作为新的分解信号,重复步骤(1)~(3),直到得到单调的基线信号.
经ITD法分解后的各PR分量是单组分的信号分量,对PRi,i∈(1,2,…,k+1)分别进行Hilbert变换得到相对应的解析信号:
(5)
其中,![]() 表示PRi(t)的Hilbert变换,即:
表示PRi(t)的Hilbert变换,即:
(6)
ai(t)=![]() 1/2;
1/2;
(7)
(8)
定义瞬时频率为:
(9)
1.2 端点延拓算法
由于信号的两端点不是极值点,ITD法利用两端点的数据计算基线信号并不合适.在此,对信号进行端点延拓,得到其在端点处的合理的极值点数据.由此,经过端点延拓改进的ITD法称为IITD法.
在信号的两端分别延拓1个极大值点和1个极小值点即可,具体延拓方法如下.
对于离散时间序列信号:
t∈[t(1),t(2),…,t(n)]=[t1,t2,…,tn].
(10)
x(t)∈ [x(t1),x(t2),…,x(tn)]=
[x1,x2,…,xn].
(11)
设信号的采样时间步长为Δt,其包含M个极大值和N个极小值,相应的极值点坐标序列为(Im,In),时刻为(Tm,Tn),函数值为(U,V).
假设信号左端的第一个特征波内包含k1个离散点,则信号左端点处向外延拓的极值点的时刻(Tm,Tn)和函数值(U,V)为:
(12)
同理,假设信号右端的第一个特征波内包含k2个离散点,则信号右端点处向外延拓的极值点的时刻(Tm,Tn)和函数值(U,V)为
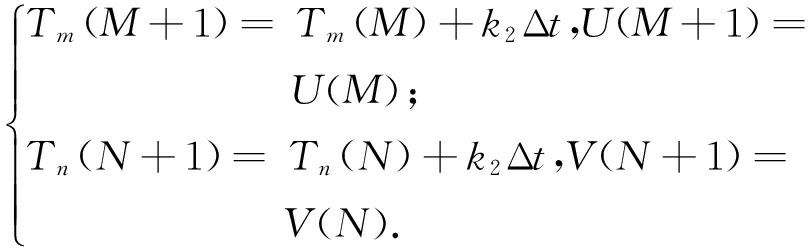
(13)
若信号的端点值大于靠近端点的第一个极大值或者小于靠近端点的第一个极小值,则端点被视为极值点.
2 模态参数辨识方法及仿真分析
根据IITD法的物理意义,获得的PR分量可以看做结构的模态响应分量,通过对PR分量进行分析,可提取结构的模态参数,以下利用IITD法辨识结构模态参数的方法称为IITD-Modal Parameter Identification法,简称IITD-MPI法,其具体原理如下.
对于一个多自由度的机械系统,脉冲激励下的位移响应可以表示成多个单自由度系统位移响应的叠加[15-16],即
![]() φi).
φi).
(14)
式中:Ai、ζi、ωni、φi分别为第i阶模态的位移幅值系数、模态阻尼比、固有角频率和初相位.
对于小阻尼情况,对比式(5)和式(14),瞬时幅值和瞬时相位可表示为:
ai(t)=Aie-ζiωnit;
(15)
![]() φi.
φi.
(16)
对式(15)两边取对数,可得:
lnai(t)=-ζiωnit+ln Ai.
(17)
根据式(16)和(17)可以得到瞬时相位曲线和对数幅值曲线,然后对其进行线性拟合,根据拟合后直线的斜率来辨识结构的模态固有频率和阻尼比.
一般地,低阶模态对机械系统位移响应起主导作用.根据式(14),构造位移响应的仿真信号为:
x![]()
(18)
取信号的采样频率为1 024 Hz,采样点数为2 048,其时域波形如图1所示.从式(18)可以看出,位移响应包含3个模态分量,若能将各阶模态从位移响应中分离出来,则可以利用上述的单自由度模态固有频率和阻尼比辨识方法,将各阶模态参数提取出来.
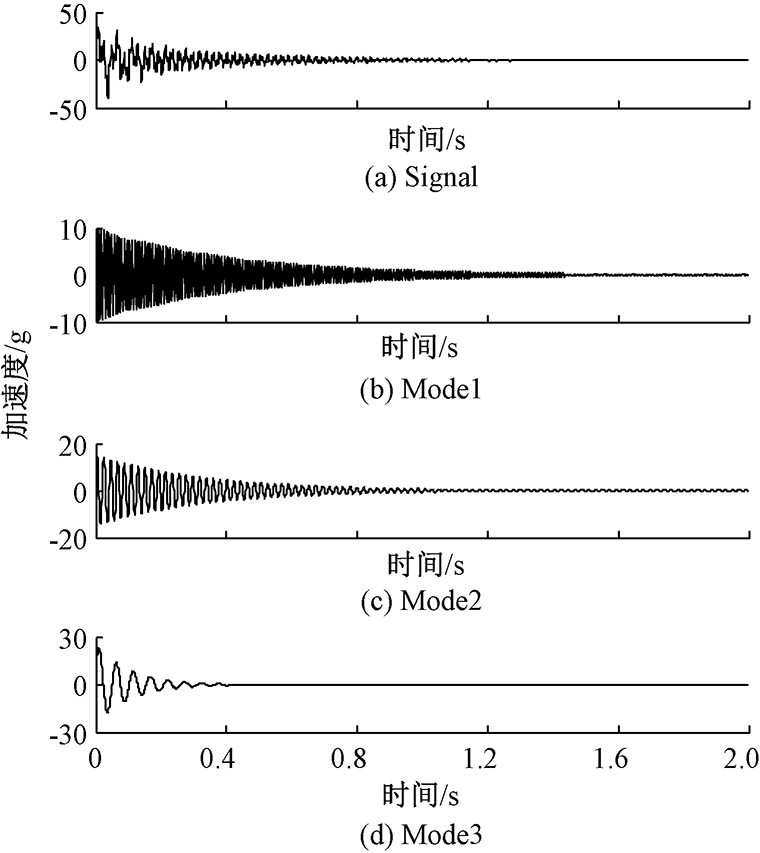
图1 位移仿真信号的时域波形
Fig.1 Time domain waveform of the displacement
simulated signal
使用IITD法将位移仿真信号进行分解,得到3个PR分量和1个余项.根据式(16)和(17)分别做3个PR分量的瞬时相位和对数幅值曲线,并对它们进行线性拟合,得到拟合直线.根据拟合直线的斜率![]() 和-ζiωni可计算得到结构的模态参数.
和-ζiωni可计算得到结构的模态参数.
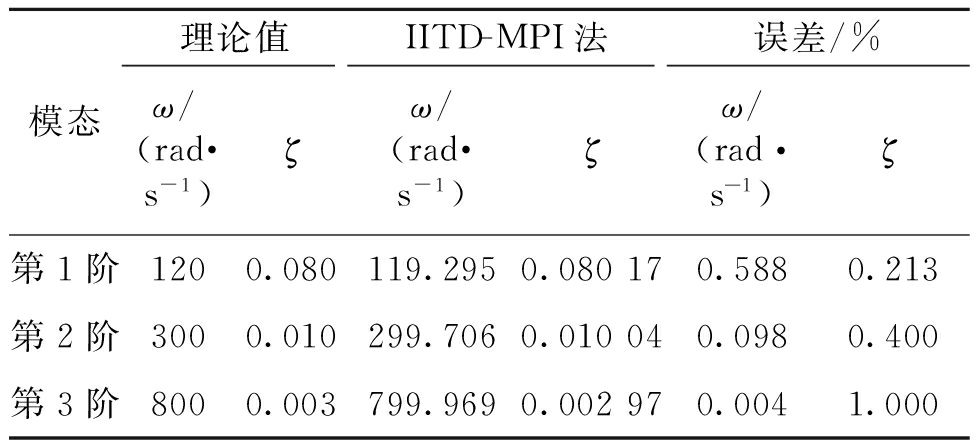
使用IITD-MPI法计算的结构模态参数与理论值的对比情况如表1所示.从表1中可以看出,IITD-MPI法可以较准确地提取位移仿真信号的3阶模态,且计算的模态固有频率和阻尼比与理论值吻合较好.模态固有频率的最大误差出现在第1阶,误差不大于0.6%.模态阻尼比的最大误差出现在第3阶,误差为1%.在文献[11]和文献[13]中,EMD-ICA法和LMD法识别的模态频率和阻尼比与理论值相比,模态频率最大误差分别为6%和大于5%,阻尼比最大误差分别为大于23%和大于17%.由此对比发现,在模态参数识别方面,IITD-MPI法的误差较EMD-ICA法和LMD法小,即IITD-MPI法在模态参数辨识精度上有优势.
表1 位移仿真信号的模态参数辨识结果
Tab.1 Modal parameter identification results of the displacement simulated signal
模态理论值IITD-MPI法误差/%ω/(rad·s-1)ζω/(rad·s-1)ζω/(rad·s-1)ζ第1阶1200.080119.2950.080170.5880.213第2阶3000.010299.7060.010040.0980.400第3阶8000.003799.9690.002970.0041.000
3 滑油管路模态参数辨识验证
对如图2所示的滑油管路进行自由状态下的静频测试,测试频率范围为0~2 000 Hz.用柔绳将滑油管路吊挂使其呈自由状态,使用PCB 352B10型加速度传感器在滑油管路上某一点拾振,用小钢棒轻敲滑油管路,滑油管路在脉冲激振力下发生振动,将加速度传感器所测得的振动响应信号接入数据采集和频谱分析系统,进行FFT分析,得到频谱图,读取谱图上各谱峰的频率值,即得到滑油管路在测试频率范围内的频率值.对频谱图上的各谱峰,可采用半功率带宽法计算得到滑油管路在某阶模态下的阻尼比.采集滑油管路测频信号及幅值谱如图3所示,从幅值谱可以看出,在0~2 000 Hz频率范围内,滑油管路存在2阶模态.

图2 滑油管路外形图
Fig.2 The shape picture of the lubricant oil pipe

图3 滑油管路测频信号时域波形及幅值谱
Fig.3 Time domain waveform and amplitude spectrum of the frequency testing signal for the lubricant oil pipe
对滑油管路测频信号进行IITD分解,分解结果如图4所示,从图4中可以看出,IITD成功将滑油管路测频信号分解成2个PR分量和1个余项,其中2个PR分量分别对应图3中幅值谱中的两阶模态.
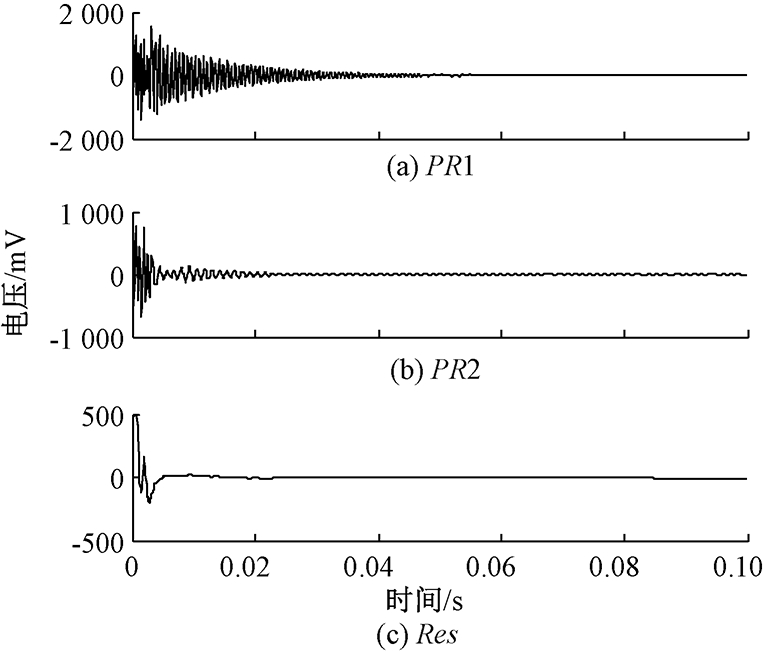
图4 滑油管路测频信号ITD分解结果
Fig.4 ITD decomposition results of the frequency testing signal for the lubricant oil pipe
同样,采用IITD-MPI法对滑油管路模态参数进行辨识并与测试模态频率以及半功率带宽法辨识的模态阻尼进行对比分析.根据式(16)和(17),绘制滑油管路测频信号的瞬时相位曲线和自然对数幅值曲线,并分别对它们进行线性拟合,得到拟合直线,见图5.同样,由拟合直线的斜率可辨识出滑油管路的模态参数.
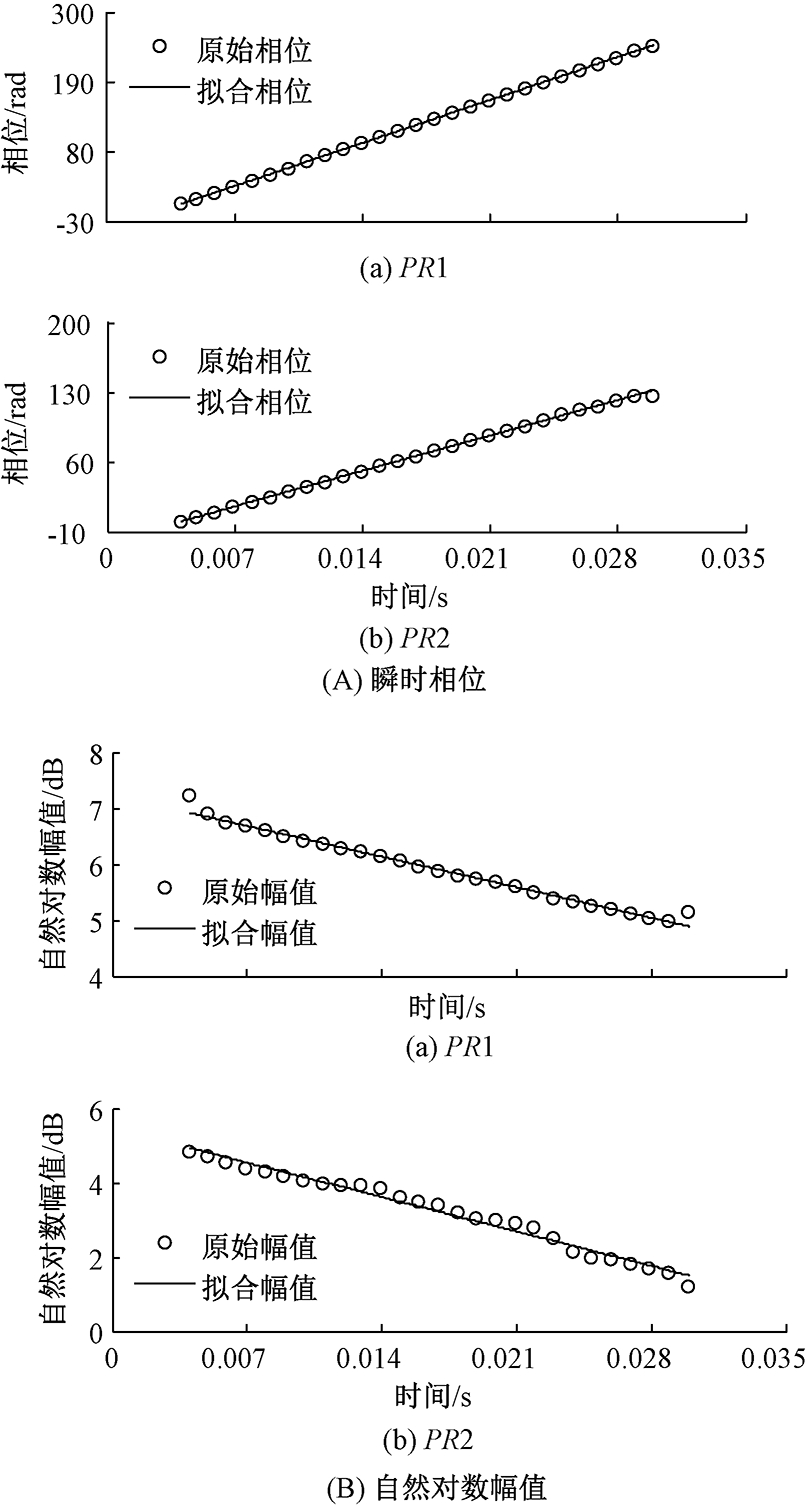
图5 滑油管路测频信号各PR分量瞬时相位和自然对数幅值
Fig.5 Instantaneous phase and natural logarithm amplitude of each PR component of the frequency testing signal for the lubricant oil pipe
滑油管路测频信号的模态参数辨识结果见表2,其中模态频率的测量值通过滑油管路的静频测试得到,模态阻尼比的测量值是使用半功率带宽法从图3所示的幅值谱中计算得到.由于受不确定性和重复性差等因素的影响,要准确辨识模态阻尼本身难度大.半功率带宽法作为阻尼辨识的最基本的方法,它也易受诸如采样频率、频率分辨率和采样分析点数等因素的影响[17],其结果仅作为参考.
表2 滑油管路测频信号模态参数辨识结果
Tab.2 Modal parameter identification results of the frequency testing signal for the lubricant oil pipe

模态测量值IITD-MPI法差别/%f/Hzζf/Hzζf/Hzζ第1阶810.550.02560809.460.026020.1341.64第2阶1542.970.008291541.230.008060.1132.77
从表2可以看出,IITD-MPI法辨识的模态频率与静频测试频率接近,其辨识的第1阶模态频率与静频测试频率的误差大于第2阶,但误差不大于0.15%.相比较于模态频率的辨识结果,IITD-MPI法辨识的阻尼比与半功率带宽法辨识的阻尼比差别相对较大,最大差别出现在第2阶,数值小于3%.综上,使用IITD-MPI法成功辨识了滑油管路的模态参数,且辨识结果准确性较高,同时也说明了对于实际测频信号的模态参数识别,IITD-MPI法也具有较好的适用性.
4 结论
(1)位移仿真信号的模态参数辨识结果表明,IITD-MPI法辨识的3阶模态固有频率与阻尼比与理论值接近,其中模态固有频率的最大误差不超过0.6%,阻尼比的最大误差不超过1%.
(2)滑油管路测频信号的模态参数辨识结果表明,所研究的滑油管路在0~2 000 Hz频率范围内,存在2阶模态,IITD-MPI法成功辨识出该2阶模态,且IITD-MPI法辨识的模态固有频率与滑油管路静频测试频率的最大误差不超过0.15%,IITD-MPI法辨识的阻尼比与半功率带宽法辨识的阻尼比最大差别小于3%.
(3)模态参数辨识的仿真分析与实验验证表明,IITD-MPI法可准确实现信号的分解,得到正确的模态分量,同时其辨识的模态参数具有较高的准确度,满足工程应用要求.但同时需要说明的是,由于IITD法仍存在一定的模态混叠现象,并且对噪声干扰比较敏感,因此,IITD-MPI法在辨识模态参数时要求信号中各模态不能太密集分布,且不能存在太强的背景噪声.若存在密集模态,IITD分解效果不好,可结合带通滤波解决.若信号被强烈的背景噪声污染,可在使用IITD法分解信号前进行滤波处理.
参考文献:
[1] 王少纯,邓宗全,高海波,等.月球着陆器用金属橡胶高低温力学性能试验研究[J].航空材料学报,2004, 24(2):27-31.
[2] 边杰,陈运西.压气机静子叶片阻尼特性试验研究[C]∥第十五届中国科协年会论文集.贵阳:中国科学技术协会,2013.
[3] 李允公,姚兆,刘杰,等.基于瞬时频率的窗宽递增寻优的短时傅里叶变换[J].东北大学学报(自然科学版),2007, 28(12):1737-1740.
[4] HE R, LUO W B, WANG B L. A new method of choosing scales in wavelet transform for damping identification [J]. Journal of harbin institute of technology (new series), 2008, 15(2): 164-166.
[5] LEI Y G, LIN J, HE Z J, et al. A review on empirical mode decomposition in fault diagnosis of rotating machinery [J]. Mechanical systems and signal processing, 2013, 35(1/2): 108-126.
[6] 韩剑鹏,鲁改凤,曹文思.基于LMD法的电力系统暂态扰动检测技术研究[J].郑州大学学报(工学版),2016, 37(1):29-33.
[7] FREI M G, OSORIO I. Intrinsic time-scale decomposition: time-frequency-energy analysis and real-time filtering of non-stationary signals [J]. Proceedings of the royal society A, 2007, 463(2078): 321-342.
[8] 胡劲松,杨世锡,吴昭同,等.旋转机械振动信号基于EMD的HT和STFT时频分析比较[J].汽轮机技术,2002, 44(6):336-338.
[9] 乔保栋,陈果,曲秀秀.基于小波变换和盲源分离的滚动轴承耦合故障诊断方法[J].机械科学与技术,2012, 31(1):53-58.
[10] 窦东阳,赵英凯.集合经验模式分解在旋转机械故障诊断中的应用[J].农业工程学报,2010, 26(2):190-196.
[11] 付春,姜绍飞.基于改进EMD-ICA的结构模态参数识别研究[J].工程力学,2013, 30(10):199-204.
[12] 张辛林,焦卫东.基于LMD EMD故障诊断分析及其研究[J].机械研究与应用,2012,21(5):156-158.
[13] 程军圣,朱文峰,李宝庆.基于LMD的模态参数识别方法[J].计算机工程与应用,2015, 51(14): 214-218.
[14] 罗颂荣,程军圣,郑近德.基于ITD分形模糊熵的轴承早期故障诊断[J].振动、测试与诊断,2013, 33(4):706-711,730.
[15] 姚千斌,杨智春,李斌.基于小波变换方法的材料小阻尼识别[J].机械科学与技术,2007, 26(7):850-855.
[16] 王超,朱宏平,王波.基于复小波变换的拉索结构阻尼比识别[J].华中科技大学学报(自然科学版),2012, 40(7):115-118.
[17] 应怀樵,刘进明,沈松.半功率带宽法与INV阻尼计法求阻尼比的研究[J].噪声与振动控制,2006, 25(2):4-6.