0 引言
CVD已成为致死率第一的慢性病［1］.定量预测发病风险，能有效降低CVD的发病率［2］.
经典的 Framingham、SCORE、WHO 等模型［3］在10年发病风险预测中已取得较好的预测效果，主要建模方法有:基于疾病流行过程和特征做出趋势性推理的预测法［4］；基于疾病危险因素、发病情况的随访队列横断面数据的数理预测法［5］.以上方法的核心是Logistic回归和Cox比例风险回归［6］.回归分析方法无法解决多分类因素的拟合问题［7］，此外，概率型策略对自变量数据要求较高，在缺乏大型横断面研究资料时应用困难.
机器学习具有较强的自学习、自适应能力，能够有效处理医疗信息中模糊、非线性数据［8］，为解决此类问题提供了新思路.笔者以构建网络预测模型为切入点，改变传统公式化预测模型，建立机器学习模型，从而拓展模型预测因素，提高预测能力.首先建立 ELM［9］模型；然后引入 ELPSO优化算法［10］，构建 ELPSO-ELM 模型；最后利用文献［14］、［15］数据集验证模型性能.实验表明，所设计算法的AUC值均高于传统模型的AUC值(0.76～0.80)，可见笔者算法能较好地实现CVD预测.
1 传统模型问题分析
以Logistic回归方法为例.
给定n组包含k个危险因素的观测样本(xi1，xi2，…，xik；yi)(i=1，2，…，n)，yi=0 表示未得病，yi=1表示得病，二元Logistic回归方程式为:
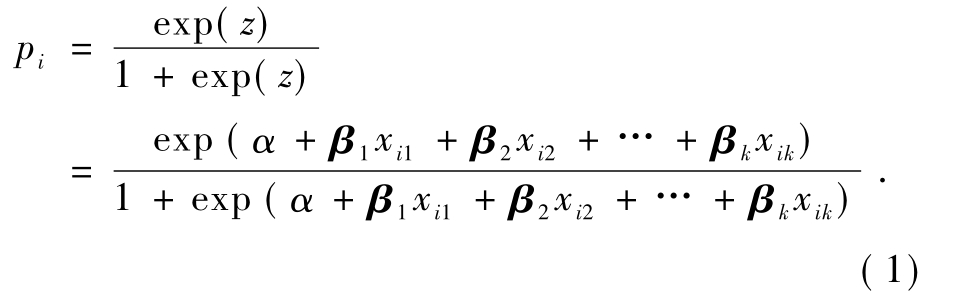
对式(1)取 Logistic变换，得 Logistic回归预测模型:
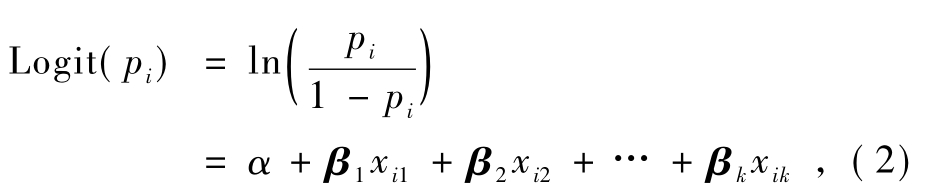
式中:α为回归截距；βi为自变量的回归系数.用最大似然函数法求各参数值.
在回归问题中，当危险因素必须以多分类定性变量才能完全表述时，一般顺序赋值为1、2、…、n，此时带来的问题包括:①无序多分类变量被视作连续变量；②有序多分类变量，强行规定无法准确衡量类别间差距的变量为等距.上述问题丢失了数据的真实信息，模型误差较大.Logistic回归中，上述问题可通过人为地设置哑变量［11］(记作Dv-Logistic的方法)将多分类转换成二分类解决.但对于包含较多复杂因素的医疗数据，该方法建模困难且易出错，无法自动建立预测模型.
2 基于极限学习机和粒子群算法的预测模型
2.1 极限学习机(ELM)
极限学习机(extreme learning machine，ELM)是基于单隐层前馈神经网络［12］的机器学习算法.给 定 n 组 训 练 样 本 (xi，yi)，xi= (xi1，xi2，…，xil)Τ、yi=(yi1，yi2，…，yim)Τ 分别为 l维输入和 m维输出，设定隐单元个数为k，则网络模型为:
式中:g(x)为激活函数；βi为第 i个隐单元的输出权重；wi为第i个隐单元的输入权重；bi为第 i个隐单元的阈值.
极限学习机能够使输出值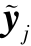 
以零误差逼近真实值 yj，即存在 βi、wi和 bi，使得
表示为矩阵形式，为:
式中:Η为隐层输出矩阵；Y为模型输出矩阵.
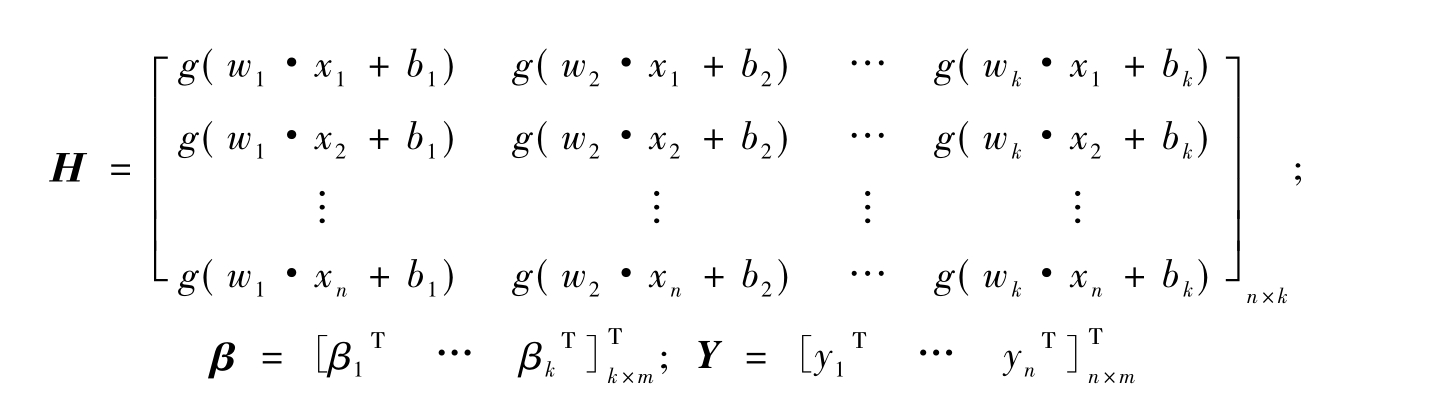
式(5)的最小范式最小二乘解为:
式中:Η+为隐层输出矩阵Η的Moore-Penrose广义逆.
2.2 ELM模型稳定性改进
2.2.1 问题分析
ELM随机初始化隐单元参数，由式(3)知，随机化过程中可能出现影响较小或无效单元［9］，需要设置大量的隐单元才能达到理想效果.而ELM测试复杂度为 O(Nlk2m)，N(测试样本数)、l(输入特征维数)、m(输出标签维数)均确定，为降低复杂度则要求在误差允许范围内k尽可能小.
另外，样本可能存在复共线性问题，每次ELM求解的Moore-Penrose广义逆Η+可能不同，导致求出的隐层输出权重不同，使得ELM模型泛化能力和预测稳定性不足.
2.2.2 粒子群(PSO)优化算法
针对ELM随机初始化隐单元参数导致的问题，采用基于群体演化的PSO算法进行优化.
设D维搜索空间有N个粒子，第i个粒子位置和速度分别为 Χi=(xi1，…，xid，…，xiD) 和 Vi=(vi1，…，vid，…，viD)，每个粒子能记忆粒子自身历史最优位置 Pi=(pi1，…，pid，…，piD)、个体极值pbest、群体历史最优位置 Pg= (pg1，…，pgd，…，pgD)和全局极值gbest，每次迭代过程中，粒子速度和位置分别通过方程(7)、(8)更新，
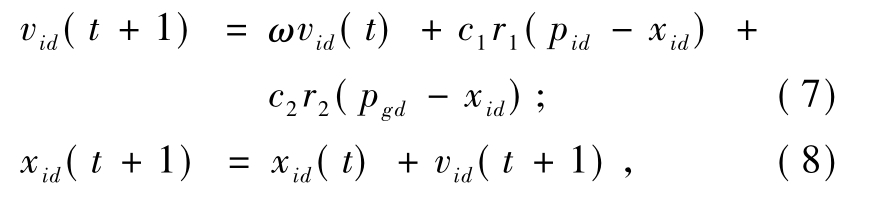
式中:ω 为惯性权重；c1、c2为学习因子；r1、r2为［0，1］上相互独立的随机数.
针对PSO易过早收敛陷入局部最优且无法自动跳进的问题，采用增强领导粒子的PSO算法(enhanced leader PSO，ELPSO)，通过提高群体领导粒子的质量，增强PSO的搜索性能.
2.3 ELPSO-ELM混合智能算法
以ELM的输入权值矩阵wi和隐单元阈值bi为ELPSO的粒子，设计ELPSO-ELM算法模型.
算法1 ELPSO-ELM算法
输入:数据集实例 (xi，yi)
输出:概率矩阵Y
Step1:初始化算法参数.粒子群规模N为40，迭代次数 tmax=30，惯性权重 ωmax=0.9、ωmin=0.4，c1=c2=2，r1、r2为［0，1］上随机数；ELM 隐单元个数k设定为20.PSO维数计算公式为D=k(n+1)，n为每个粒子的维数.第 i个粒子表 示 为
取值范围分别为［-1，1］、［0，1］.
Step2:选择sigmoid函数为ELM算法的激活函数，根据式(3)～(5)计算输出权重矩阵，反推得到输出矩阵Y'，计算Y'与训练数据真实值Y的均方根误差(RMSE)，以 RMSE为粒子的适应度值，以具有较小适应度值的粒子为更优粒子［13］.
Step3:根据式(7)、(8)更新粒子.ELPSO算法中，每次迭代过程中对领导粒子Pg依次进行五阶段连续变异，分别为Gaussian变异、Cauchy变异、Pg各 维 opposition-based 变 异、Pg整 体opposition-based变异和DE-based变异，每次变异选取适应度值最小的粒子为种群领导粒子.
Step4:判断是否达到最大迭代数.若达到，则输出全局最优粒子；若未达到，先利用式ω=ωmax-(ωmax-ωmin) ×t/tmax更新惯性权重，再返回Step2继续执行.
Step5:最终ELPSO输出的粒子即为wi和 bi的最佳取值，再用ELM建立预测模型，导入测试数据进行回归计算，得到真实数据集的预测结果.
3 实验分析
3.1 数据集
以 UCI机器学习库的 Statlog(Heart)［14］数据集和 Heart Disease Database［15］验证模型，两数据集分别包含270和820组实例，每组实例包含13个属性和1个分类标签值.数据的属性如表1.
表1 数据集共同的特征属性
Tab.1 The same attributes in two datasets
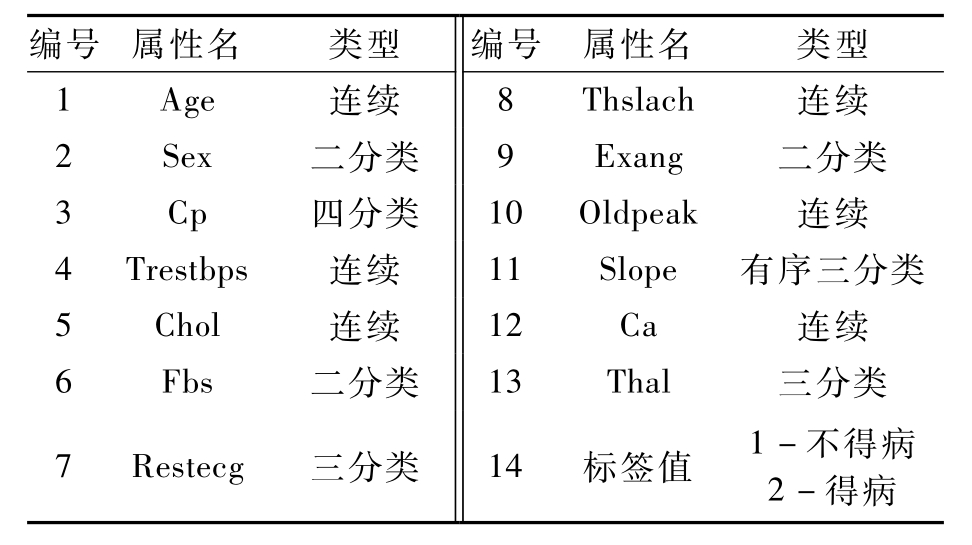
编号 属性名 类型 编号 属性名 类型1 A g e 连续 8 T h s l a c h 连续2 S e x 二分类 9 E x a n g 二分类3 C p 四分类 1 0 O l d p e a k 连续4 T r e s t b p s 连续 1 1 S l o p e 有序三分类5 C h o l 连续 1 2 C a 连续6 F b s 二分类 1 3 T h a l 三分类7 R e s t e c g 三分类 1 4 标签值 1-不得病2-得病
3.2 实验设计
实验一:利用二元Logistic回归分析训练数据，求得参数 (α，β1，…，β11) 值，根据式(1)建立Logistic预测方程，代入测试数据的属性值，对比所得预测值与真实标签值计算出预测正确率.
实验二:对多分类属性设置哑变量，然后对数据利用实验一方法进行Logistic回归分析.
实验三:利用ELPSO-ELM对原始数据进行实验，算法参数初始化如 Step1.因 ELPSO每次寻优参数不同，导致模型预测结果有所波动，因此选择30次预测结果的均值作为最终值.
实验四:为保证在同一计算代价下验证算法，组建ELM随机搜索组合算法(ELMs).ELPSOELM单次运行适应度值的评价次数为(40+5)×30；组合PSO-ELM算法作对比，其粒子规模设置为30、迭代45次；ELMs算法中每次 ELM运行次数为45×30次，选择其中训练误差最优的测试结果作为ELMs算法的输出.
3.3 实验结果
(1)统计 Logistic、Dv-Logistic、ELM、ELMs、PSO-ELM、ELPSO-ELM模型各30组预测结果的真阳性(TP)、假阳性(FP)、真阴性(TN)、假阴性(FN)，利用均值计算灵敏度、特异性及正确率，结果见表2.
(2)ROC曲线.利用受试者工作特征曲线(ROC)［16］评定预测模型性能，以 AUC大小表示ROC曲线结果的好坏.AUC值在0.5～0.7时具有较低的准确性，在0.7～0.9时具有一定的准确性，在0.9以上时具有较高的准确性.各模型ROC曲线如图1.
3.4 ELPSO-ELM模型性能参数分析
3.4.1 ELPSO参数分析
(1)惯性权重 ω.ω 一般取值在［0，1］，稍大的ω利于扩大群体搜索范围，稍小的ω利于收敛到最优位置.据此，使ω值随迭代次数线性变小，以保证ELPSO具有最优的效果.
(2)学习因子 c1、c2.由式(7) 知，c1过大则粒子较多地在局部范围搜索，c2过大则粒子过早收敛，结合大量实验，最终选定c1=c2=2.
(3)粒子群规模.一般优化问题在［20，50］取值，粒子数量设置过小，对结果偏差影响较大.综合考虑ELPSO的优化维度，平衡模型稳定性、正确率和快速性，将粒子数设置为40.
3.4.2 ELM参数及结果影响
由于ELM随机初始化隐单元参数，预测模型稳定性较低.在各模型最佳隐单元个数下做30次重复实验，预测结果以方差表示，如表2.
对比各模型方差可知，ELM结果波动较大，且正确率不高；ELMs因选择多次运行中的最优值，结果变动不大，但正确率不高；ELPSO-ELM在保证模型稳定性的同时较大地提高了正确率.
表2 各模型预测结果对比
Tab.2 Results contrast of each prediction model
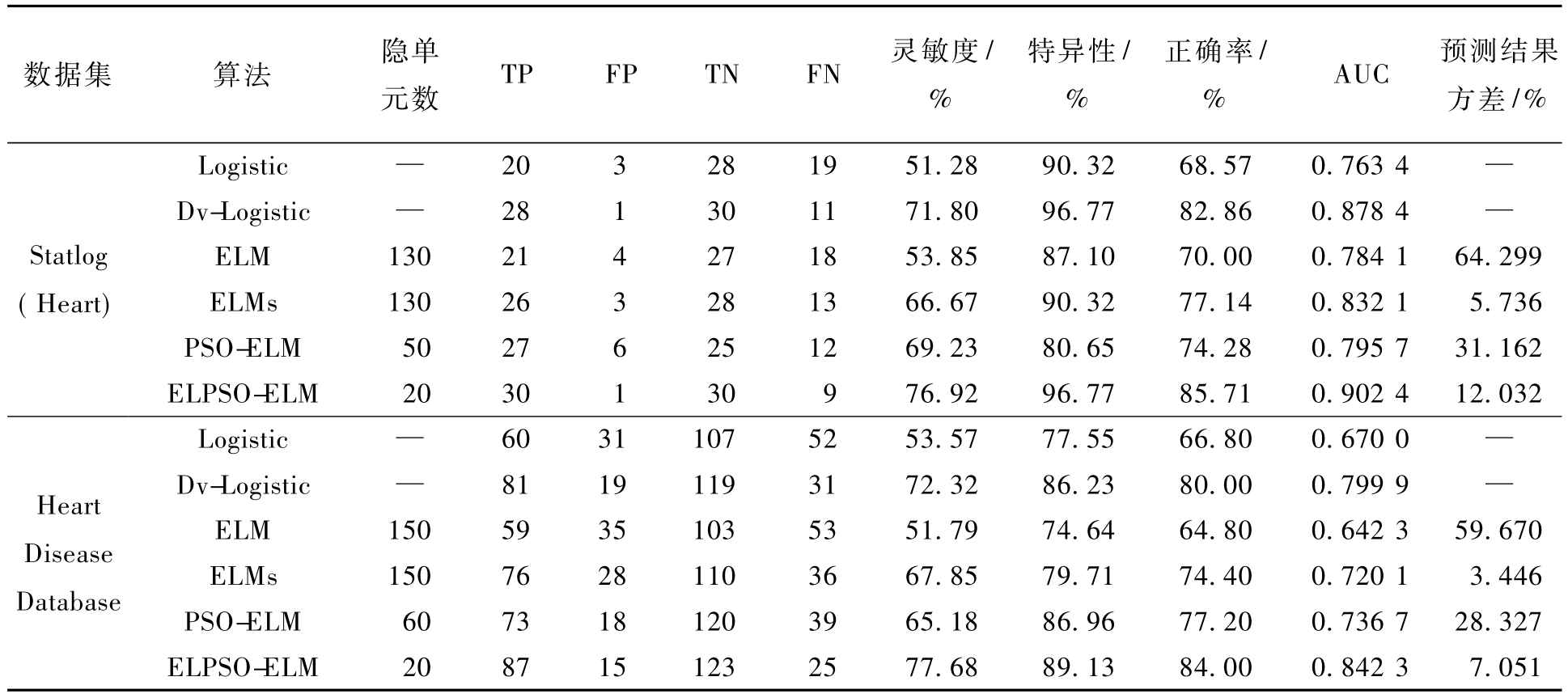
数据集 算法 隐单元数 TP FP TN FN 灵敏度/%特异性/%正确率/% AUC 预测结果方差/%Logistic—203281951.2890.3268.570.763 4—Statlog(Heart)Dv-Logistic—281301171.8096.7782.860.878 4—ELM 130 21 4 27 18 53.85 87.10 70.00 0.784 1 64.299 ELMs 130 26 3 28 13 66.67 90.32 77.14 0.832 1 5.736 PSO-ELM 50 27 6 25 12 69.23 80.65 74.28 0.795 7 31.162 ELPSO-ELM 20 30 1 30 9 76.92 96.77 85.71 0.902 4 12.032 Logistic—60311075253.5777.5566.800.670 0—Heart Disease Database Dv-Logistic—81191193172.3286.2380.000.799 9—ELM 150 59 35 103 53 51.79 74.64 64.80 0.642 3 59.670 ELMs 150 76 28 110 36 67.85 79.71 74.40 0.720 1 3.446 PSO-ELM 60 73 18 120 39 65.18 86.96 77.20 0.736 7 28.327 ELPSO-ELM 20 87 15 123 25 77.68 89.13 84.00 0.842 3 7.051
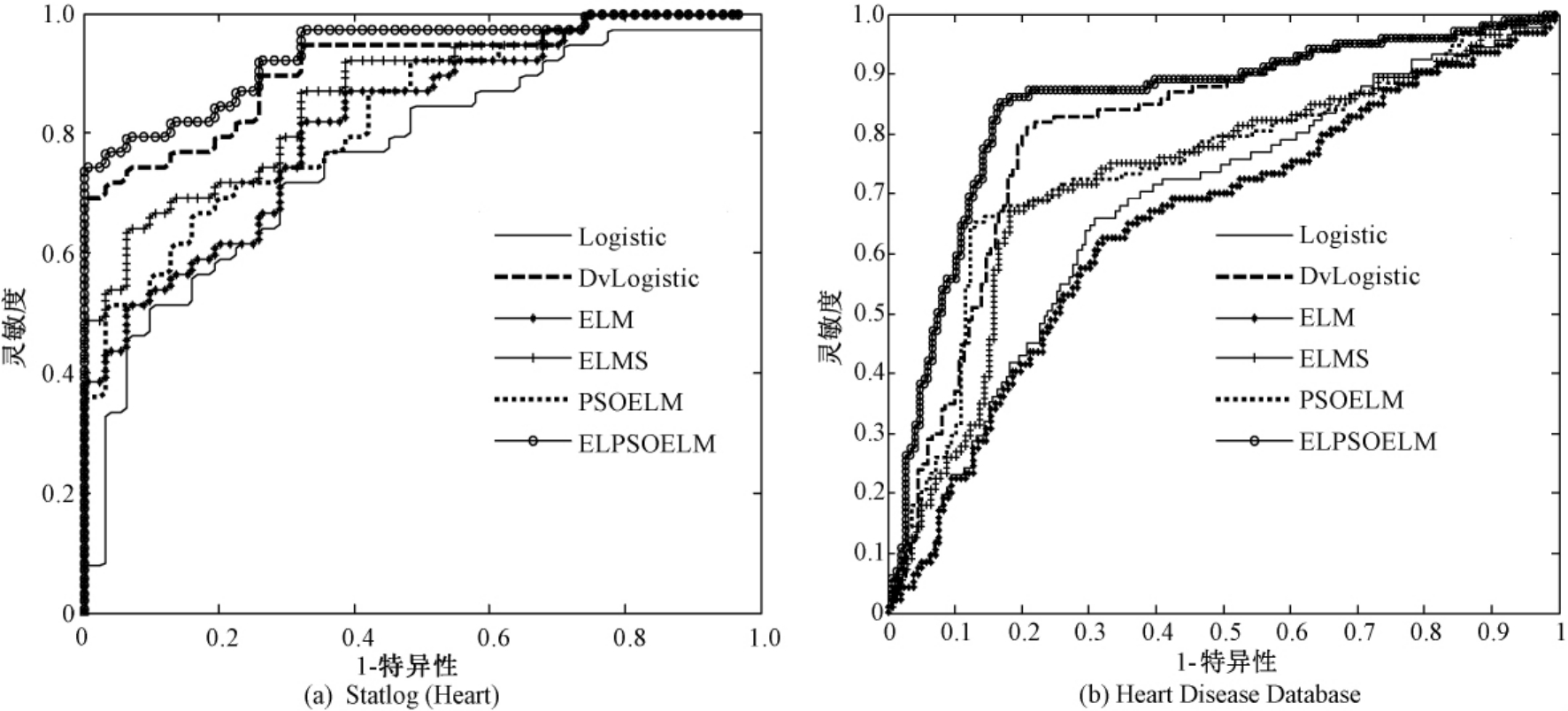
图1 ROC曲线图对比
Fig.1 Comparison of ROC curves
以Statlog(Heart)数据集为例.在相同的计算代价下，ELM隐单元个数对模型的影响如表3.
4 结论
表3 隐单元个数对模型性能影响
Tab.3 Influence of models performance by the number of hidden neurons
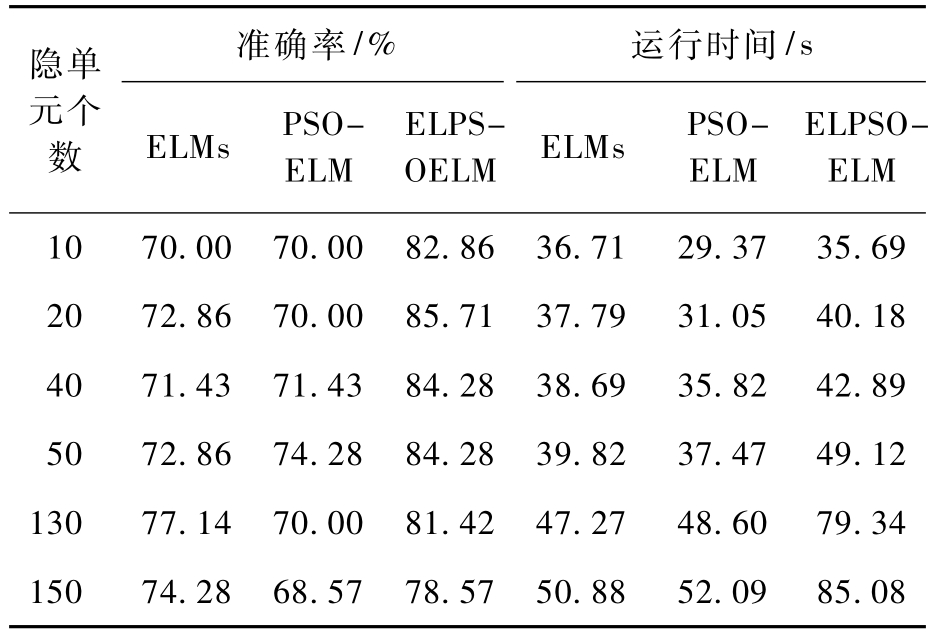
隐单元个准确率/% 运行时间/s ELMs PSOELM OELM ELMs PSOELM ELPS-ELPSO-数ELM 10 70.00 70.00 82.86 36.71 29.37 35.69 20 72.86 70.00 85.71 37.79 31.05 40.18 40 71.43 71.43 84.28 38.69 35.82 42.89 50 72.86 74.28 84.28 39.82 37.47 49.12 130 77.14 70.00 81.42 47.27 48.60 79.34 150 74.28 68.57 78.57 50.88 52.09 85.08
(1)对多分类变量设置哑变量能较大地提高Logistic回归模型的正确率.
(2)提出的ELPSO-ELM模型，在避免设置哑变量出现人为误差和较大工作量的同时，提高了模型预测正确率，AUC值大于或接近0.9，准确率较高.
(3)利用ELPSO优化ELM，相对于ELM方法和标准PSO优化方法，减少了隐层单元数目，提高了正确率，进一步证明所提方法的有效性.
(4)实验中，粒子群优化的计算维度达到240维，提高了数据处理复杂性，且 ELPSO五阶段连续变异策略需进行大量迭代搜索，在提高模型稳定性和预测正确率的同时一定程度上降低了ELM的速度.
［1］陈伟伟，高润霖，刘力生，等.中国心血管病报告2013概要［J］.中国循环杂志，2014，29(7):487-491.
［2］COHNJ N.Prevention of cardiovascular disease ［J］.Trends in cardiovascular medicine，2015，25(5):436-442.
［3］ZHAO D，LIU J，XIE W X，et al.Cardiovascular risk assessment:a global perspective ［J］.Nature reviews cardiology，2015，12(5):301-311.
［4］HERVAS R，FONTECHA J，AUSIN D，et al.Mobile monitoring and reasoning methods to prevent cardiovascular diseases［J］.Sensors，2013，13(5):6524-6541.
［5］GAMMON K.Mathematicalmodelling:forecasting cancer［J］.Nature，2012，491(7425):S66-67.
［6］KLEBER M E，DELGADO G，GRAMMER T B，et al.Uric acid and cardiovascular events:a mendelian randomization study［J］.Journal of the American society of nephrology，2015，26(11):2831-2838.
［7］ALEXANDRE C M，FARDN.Binary logistic regression and PHM analysis for reliability data［J］.International journal of reliability，quality and safety engineering，2014，21(5):1-30.
［8］DEO R C.Machine learning in medicine ［J］.Circulation，2015，132(20):1920-1930.
［9］HUANG G B，ZHOU H，DING X J，et al.Extreme learning machine for regression and multiclass classification［J］.IEEE transactions on systems，man and cybernetics，Part 6，2012，42(2):513-529.
［10］JORDEHI A R.Enhanced leader PSO(ELPSO):a new PSO variant for solving global optimization problems［J］.Applied soft computing，2015，26:401-417.
［11］TSOUAC M，CHIS P，HUANG D Y.Edlrte:Entropybased dummy variables logistic regression tree［J］.Intelligent data analysis，2010，14(6):683-700.
［12］MAN Z H，KEVIN L，WANG D H，et al.A new robust training algorithm for a class of single-hidden layer feed-forward neural networks［J］.Neurocomputing，2011，74(16):2491-2501.
［13］王杰，苌群康，彭金柱.极限学习机优化及其拟合性分析［J］.郑州大学学报(工学版)，2016，37(2):20-24.
［14］Statlog(Heart)Data Set［B/OL］.(2004)［2016-05-20］.http://archive.ics.uci.edu/ml/datasets/Statlog+Heart.
［15］Heart Disease Data Set［B/OL］.(1988-7)［2016-05-20］.http://archive.ics.uci.edu/ml/datasets/Heart+Disease.
［16］KHREICH W，GRANGER E，MIRI A，et al.Adaptive ROC-based ensembles of HMMs applied to anomaly detection［J］.Pattern recognition，2012，45(1):208-230.