0 引言
随着建筑结构趋向于多样化、异型化、不规则化以及大空间对建筑构造的要求,斜柱钢结构开始涌现。但斜柱钢结构主要以钢斜柱与基础承台连接[1],基础承台在斜柱结构荷载传递中承受较大的水平荷载,施工过程若未控制斜柱结构内力及基础位移,可能导致基础变形甚至破坏,危害整体结构安全。目前,对于斜柱钢结构基础的相关研究较少。杨伟等[2]对北京机场航站楼上部钢结构进行施工过程监控,保证了施工的安全。刘学武[3]采用单元生死技术,对钢结构的施工全过程中内力和变形情况进行跟踪分析,并采用分阶段综合迭代法给出了构件的加工和安装预调值。Zhang等[4]和Tian等[5]进行大跨钢结构施工力学仿真,探究路径效应、温度等因素对分析结果的影响。由此可见,关于大跨钢结构的模拟方法及施工监测研究大多以上部结构为对象[6-7],对于斜柱钢结构基础施工过程中内力及位移监测和控制的研究比较缺乏。
本文依托洛阳应天门大型遗址保护斜柱钢结构建筑,各承台之间设置预应力系梁且分阶段张拉以平衡水平分力。随着施工的推进,斜柱结构基础承受斜柱水平分力不断增大,预应力张拉后又承受反向荷载作用。为对结构施工过程中的内力和基础水平位移变化跟踪分析,基于Midas Gen建立全施工阶段有限元模型,研究系梁数量、刚度、预应力对斜柱基础位移及结构内力的影响规律,为同类建筑的设计提供技术参考。
1 工程概况
洛阳应天门遗址保护建筑分为城楼、东西朵楼及阙楼等5个部分[8],本文研究对象为东朵楼,其基础由4个斜柱钢对称承台及群桩组成。结构主体采用钢结构,楼面采用现浇混凝土楼板。其立面结构受力特点如图1所示,整体传力路径清晰[9],上部建筑层荷载沿立柱传递至中部城墙层,通过城墙层斜撑转换结构将其传递至下部斜柱,然后通过斜柱钢结构落地将上部荷载传递给基础承台,最后由桩基承台与群桩共同承担结构荷载。支撑斜柱与地面呈近60°夹角,位移控制尤为重要。
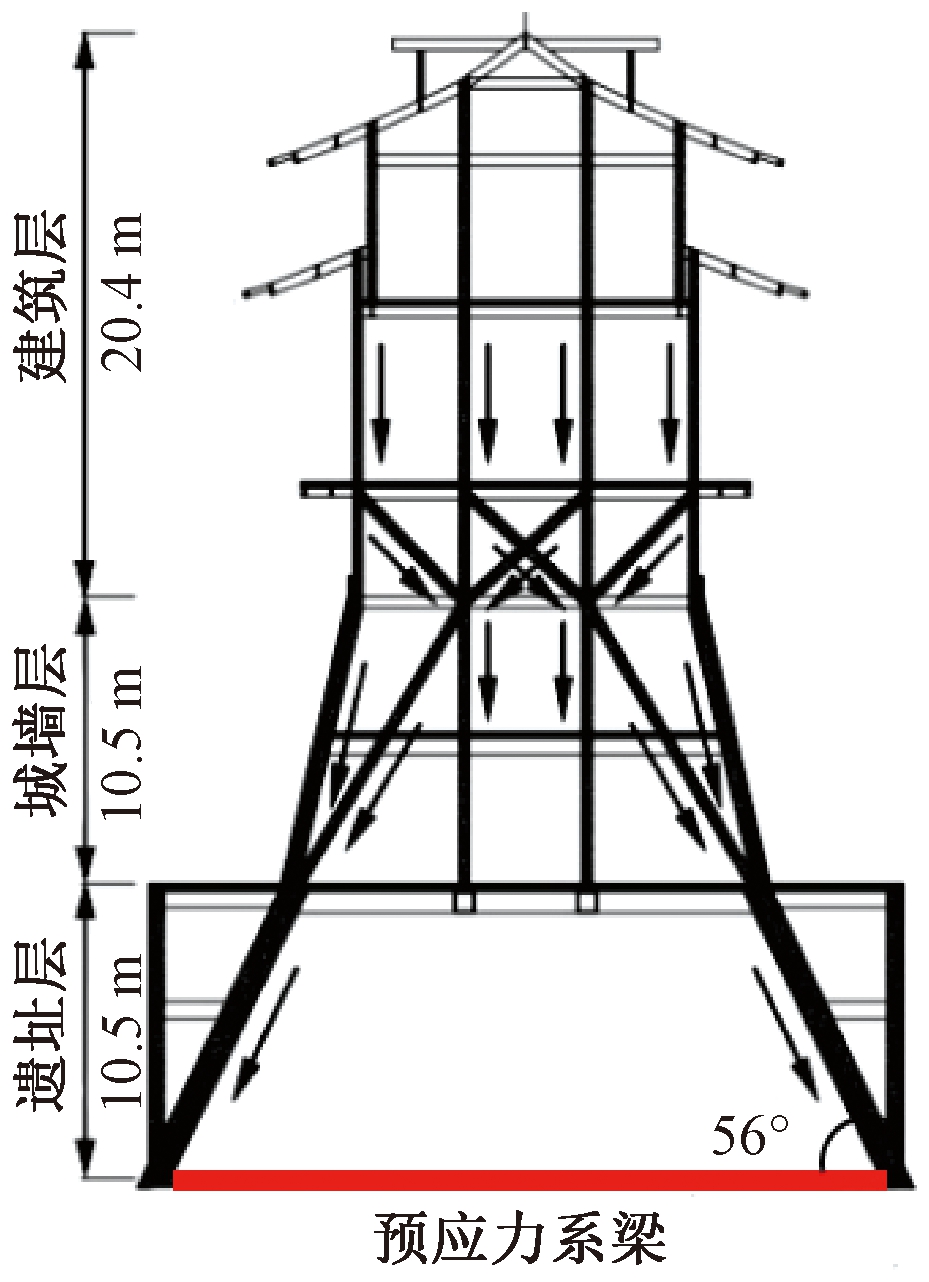
图1 东朵楼结构受力特点
Figure 1 Stress characteristics of Dongduo Building
2 分析与讨论
2.1 试验结果
根据建筑桩基技术规范,该工程单桩水平位移可取2~5 mm[10],而现场单桩水平静载试验结果表明,试验桩的水平临界荷载为280 kN,临界水平位移为2.0 mm。为控制桩顶位移,进而保障结构施工及运营安全,取施工阶段位移限值为±2.0 mm;使用阶段位移限值为±1.5 mm。
基础承台内部钢柱脚钢材强度等级为Q390,混凝土强度等级为C45。采用Midas Gen 2019建模,建模中主体钢结构选用梁单元,各层楼面、屋面及钢挑檐采用板单元进行模拟,承台混凝土及地基土体选用实体单元。钢结构主体框架梁采用600 mm×1 000 mm×40 mm×40 mm焊接箱型截面,斜柱为800 mm×1 000 mm×60 mm×60 mm焊接箱型截面。上部钢结构、下部斜柱柱脚及基础承台间均采用共节点进行连接;承台、系梁及柱脚之间采用刚性连接。假设土体为理想弹性体,土体单元力学性能参数根据地勘报告(见表1)计算。土体计算宽度从承台外边缘向外扩展1倍桩长,约20 m[11-12]。土体顶面自由,侧面施加法向固定约束,底面固结。
表1 项目场址的地质信息
Table 1 Geological information of the project

土层土层信息杂填土Q2ml4,结构疏松,层厚1.0~5.8 m黄土状粉质黏土夹粉土Q2al+pl4,压缩系数0.229 MPa-1,属中压缩性,层厚0.7~5.2m黄土状粉质黏土Q1al+pl3,压缩系数0.209 MPa-1,属中压缩性,层厚2.5~5.2 m黄土状粉质黏土Qal+pl3,压缩系数0.236 MPa-1,属中压缩性,厚度1.7~5.6 m黄土状粉土夹粉细砂Qal+pl3,压缩系数0.209 MPa-1,属中压缩性,层厚0.5~5.0 m卵石Qal+pl3,石英岩、安山岩为主,一般粒径2~6 cm,最大粒径10 cm,磨圆度较好,中密状,层厚7.2~14.0 m
注:Q为土层分类。
为了考虑系梁数量、刚度、预应力因素对施工全过程的受力影响,基于上述建模方法建立4种有限元模型,分别为模型A0,不加基础系梁;模型A1,添加预应力;模型A2,调整系梁数量;模型A3,调整系梁刚度。为进行参数分析,对模型A2、A3分别建立了若干子模型,具体见下文。部分方案的有限元模型如图2所示。
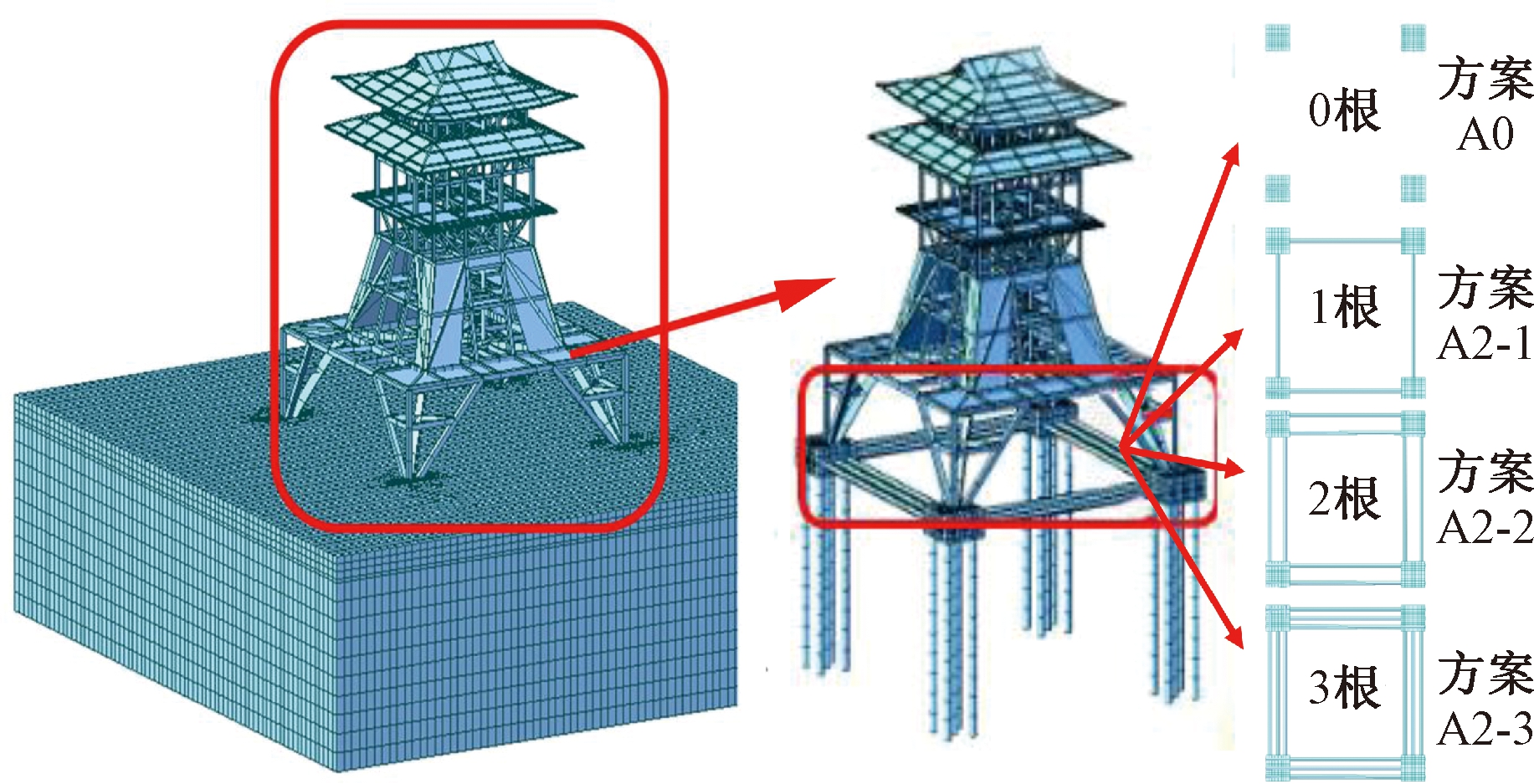
图2 东朵楼有限元模型
Figure 2 Finite element model of Dongduo Building
2.2 施工阶段划分
由于基础预应力设计值较大,基础预应力一次张拉至设计值会导致基础承受较大反方向荷载,无法保证桩基安全,故预应力采用两阶段进行张拉。
该遗址保护建筑在立面上大致分为4层,以承台顶部为0 m标高;0~8.72 m高度为下部遗址层,为主框架梁柱结构;8.72~19.32 m高度为中部城墙层,为钢框架结构;19.32~23.27 m高度为桁架转换层;23.27 m以上为上部城墙层。主要包含两层钢屋面,分别位于30.3 m及40.27 m处。结合现场施工条件东朵楼施工阶段初步划分为12个分析工况,如表2所示。
表2 东朵楼施工阶段划分
Table 2 Construction phase of Dongduo Builing

工况编号工况内容工况10~8.72 m范围内主框架工况2中部城墙层钢结构框架及8.72 m楼板工况3第一阶段预应力张拉(50%)工况423.27 m桁架转换层及29.82 m立柱工况514.22 m楼板和墙体工况6桁架转换层楼板及14.22~19.32 m墙体工况729.82 m楼板和斜撑工况829.82~40.27 m钢结构主体和第一层钢屋面工况9第二层钢屋面封顶及挑檐完成工况10第二阶段预应力张拉(100%)工况11装饰装修完成工况12使用阶段
2.3 测点布置方案
为保证结构施工过程中的安全,本文重点对斜柱钢结构基础水平位移进行监测,并辅以斜柱结构、转换桁架梁的应力监测。为方便对比,模型A0、A1、A2、A3选取相同位置布置应力及位移测点。A0模型的斜柱、桁架梁结构应力测点布置及A1模型的位移测点布置如图3、图4所示。
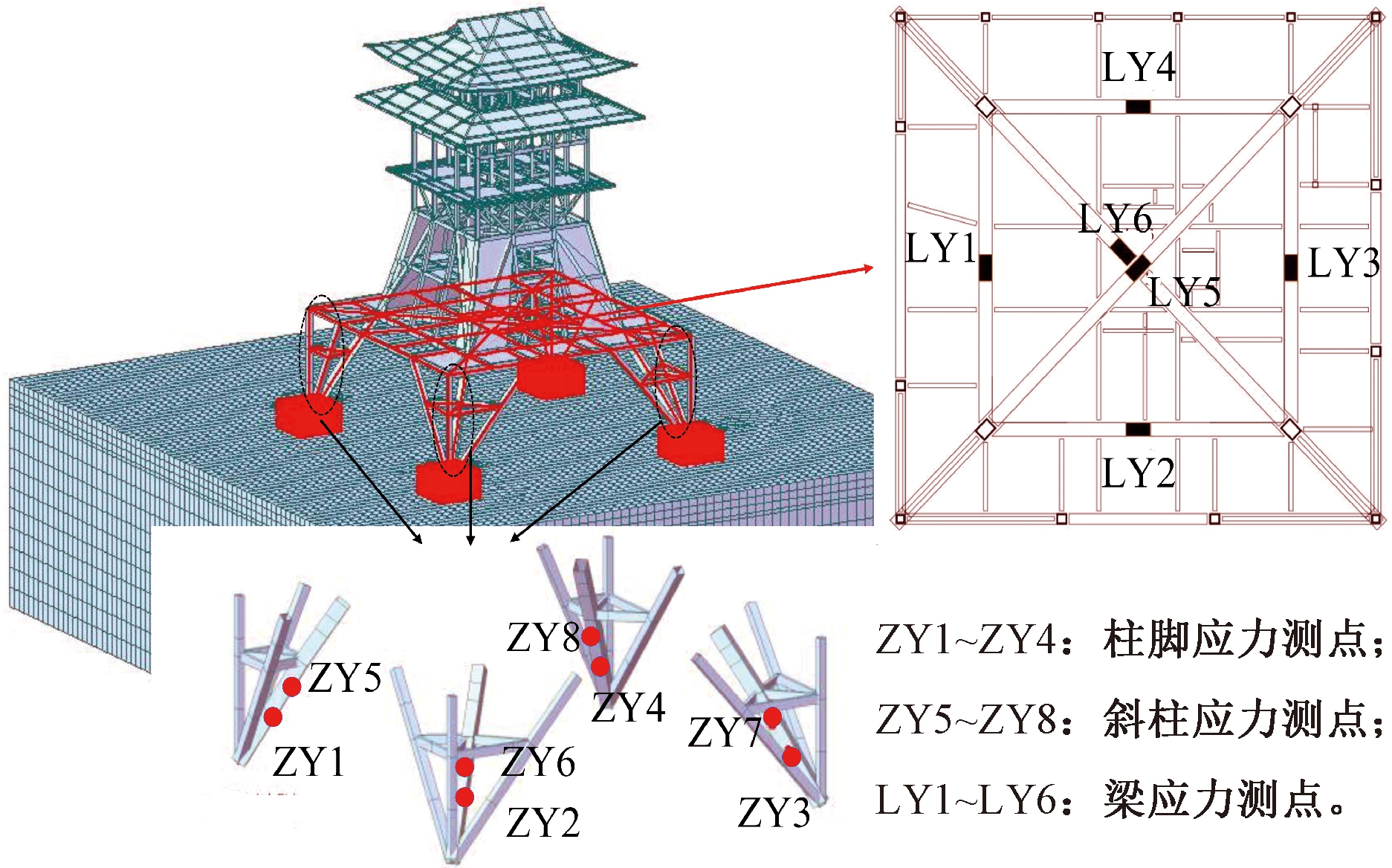
图3 模型A0应力测点布置
Figure 3 stress measurement points of A0 model
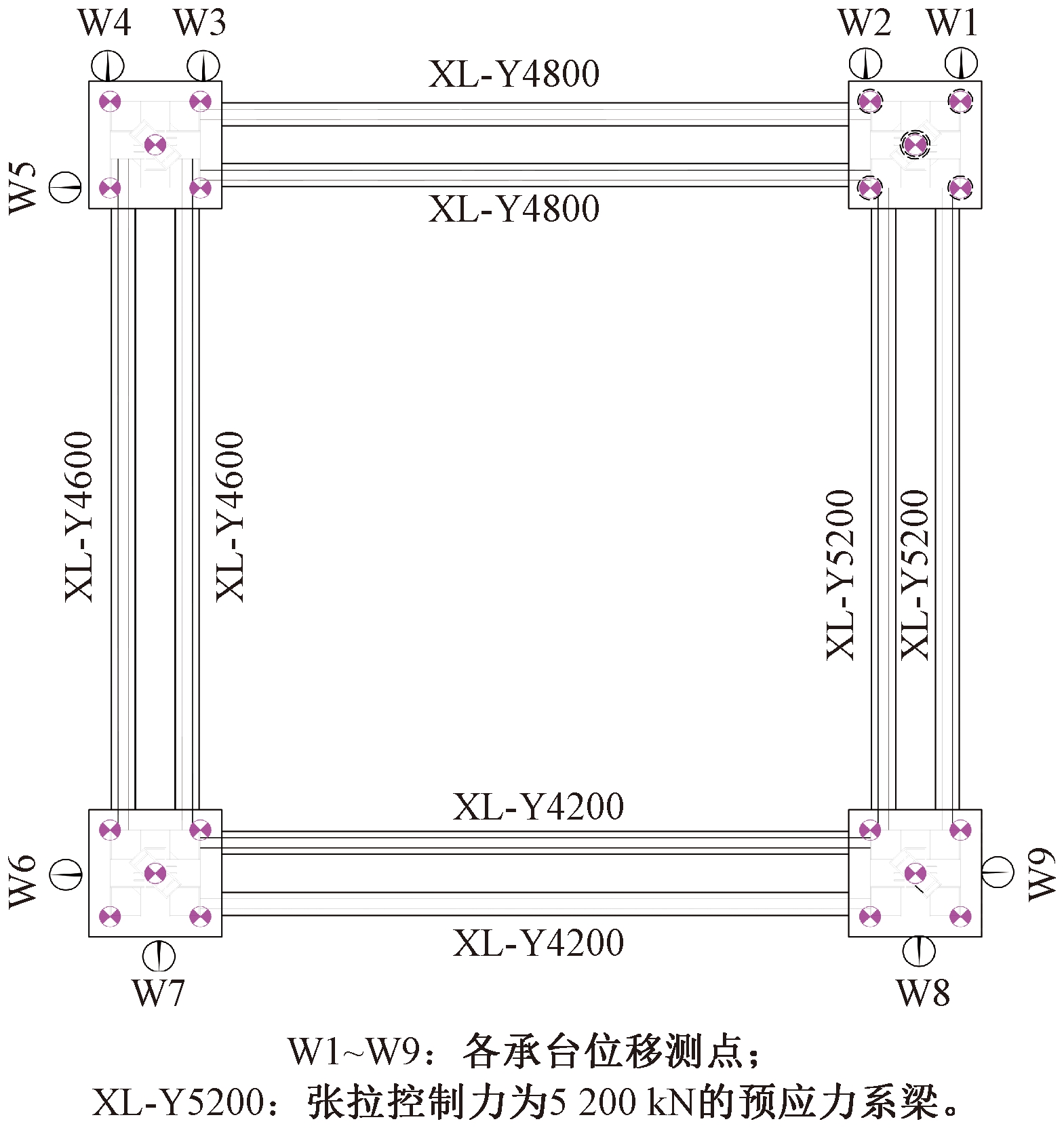
图4 模型A1位移测点布置
Figure 4 Displacement measuring points of A1 model
3 影响因素分析
3.1 预应力系梁因素对比分析
为验证设计施工方案的可行性,方案A1采用预应力基础系梁,并通过方案A1下基础水平位移与实测位移数据的对比,验证有限元模型的正确性,进而研究预应力系梁基础的受力位移变化规律。各预应力系梁的张拉力根据斜柱结构有限元模型的主斜柱底部水平分力确定,各系梁的钢绞线规格及对应的张拉控制力见表3。
表3 预应力张拉控制力
Table 3 Prestress tension control force

系梁编号张拉控制力/kN钢绞线规格XL-Y46004 60024-ϕ15.2XL-Y52005 20027-ϕ15.2XL-Y48004 80025-ϕ15.2XL-Y42004 20022-ϕ15.2
为方便表述,定义基础位移向多承台中心发展为负向,远离多承台中心发展为正向;结构应力取压应力为负,拉应力为正。图5为各施工阶段基础位移的实测值与方案A0、A1的分析值,图6为A0、A1两方案的应力分析结果。由图5可知,方案A1下基础水平位移变化趋势同现场实测情况基本一致,随着上部结构施工,基础在自重荷载等作用下发生正向位移,基础预应力张拉后,基础产生反方向水平位移。第二次预应力张拉完成后,基础最大水平位移由正向1.21 mm变化为负向0.57 mm,相对于张拉前最大变化约140%。施工阶段最大位移实测值与分析值分别为0.78、1.21 mm,使用阶段则分别为0.45、0.47 mm,均位于限值以内,基桩安全可控,预应力系梁能有效控制基础水平位移。
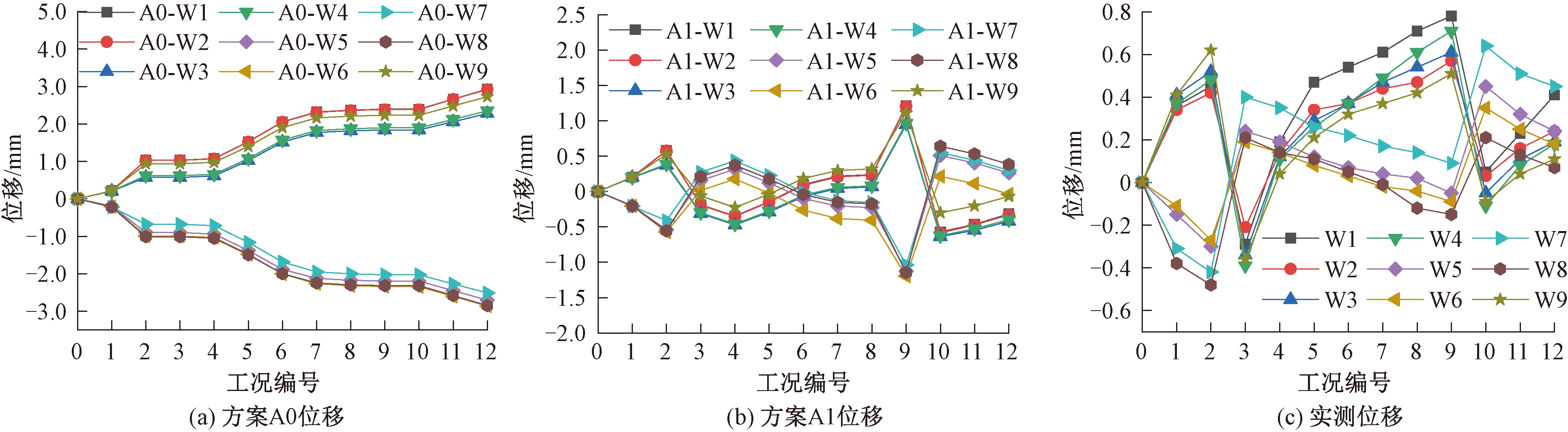
图5 基础位移对比
Figure 5 Comparison of foundation displacement
由图6可知,方案A1下两次预应力张拉完成后(工况3,工况10),钢结构柱脚关键截面应力发生反向变化,最大变化量约为10 MPa,相比张拉前最大降低约20%(ZY1测点)。施工完成后,方案A1下各柱脚截面外侧应力均低于A0方案,且各施工阶段的应力始终处于安全范围以内。故预应力系梁基础能减小斜柱结构柱脚截面的最大应力,且施工过程中不会导致柱脚局部应力激增,有利于保证结构安全。
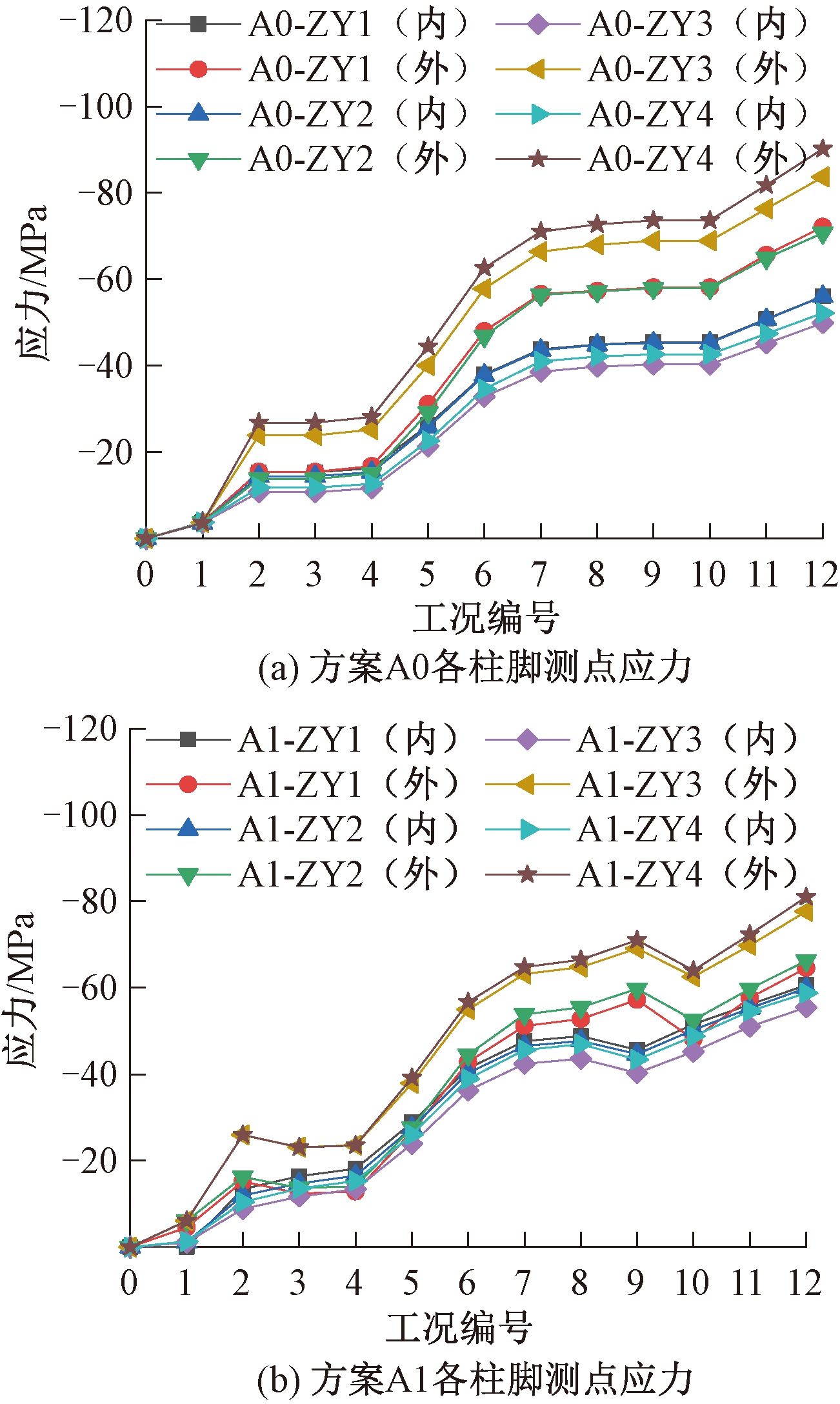
图6 方案A0和A1柱脚应力分析结果
Figure 6 Stress analysis of the plan A0 and A1 column foot
3.2 基础系梁数量影响分析
上节分析结果表明,在预应力系梁约束下,结构关键截面应力及基础位移远小于设计限值,具有较大的富余度。由于现场预应力施工存在多次张拉及预应力损失问题,故本节考虑不同数量的基础系梁代替预应力以降低施工难度(方案A2)。分别建立系梁数量分别为1根、2根、3根的子模型,相应的编号分别为A2-1、A2-2、A2-3。
选取不同位置的测点进行全施工阶段应力及位移分析,结果如图7、图8所示。由图7可知,同工况下方案A2各测点关键截面应力与方案A0的差值最大约为5.0 MPa。A2各子方案梁柱结构关键截面应力变化在2 MPa内,故系梁数量增加对结构应力影响较小。
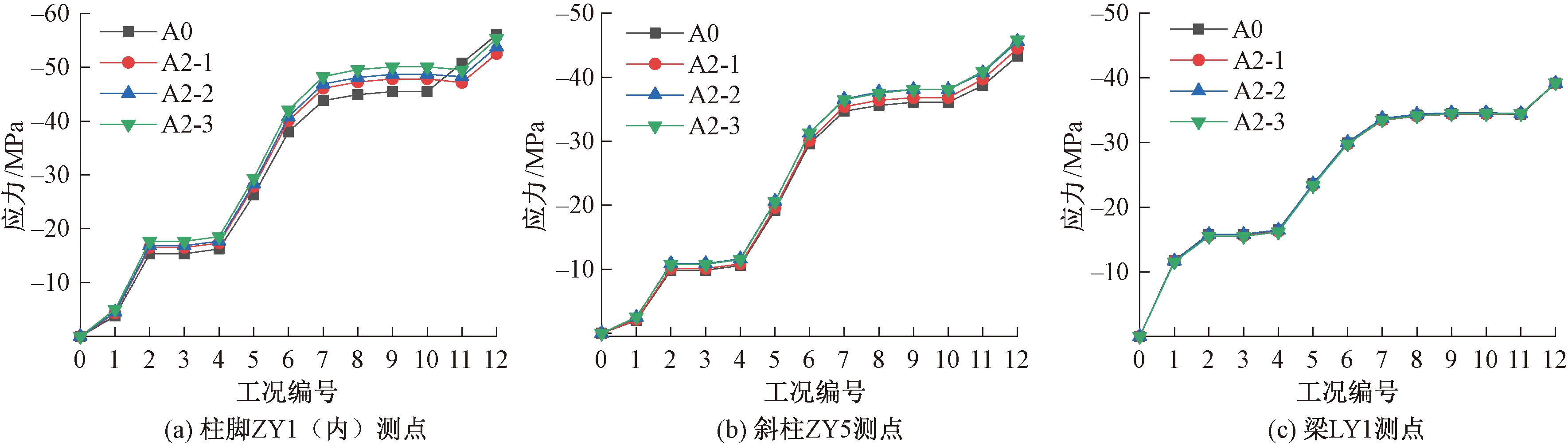
图7 方案A0和A2应力分析结果
Figure 7 Stress analysis results of scheme A0 and A2
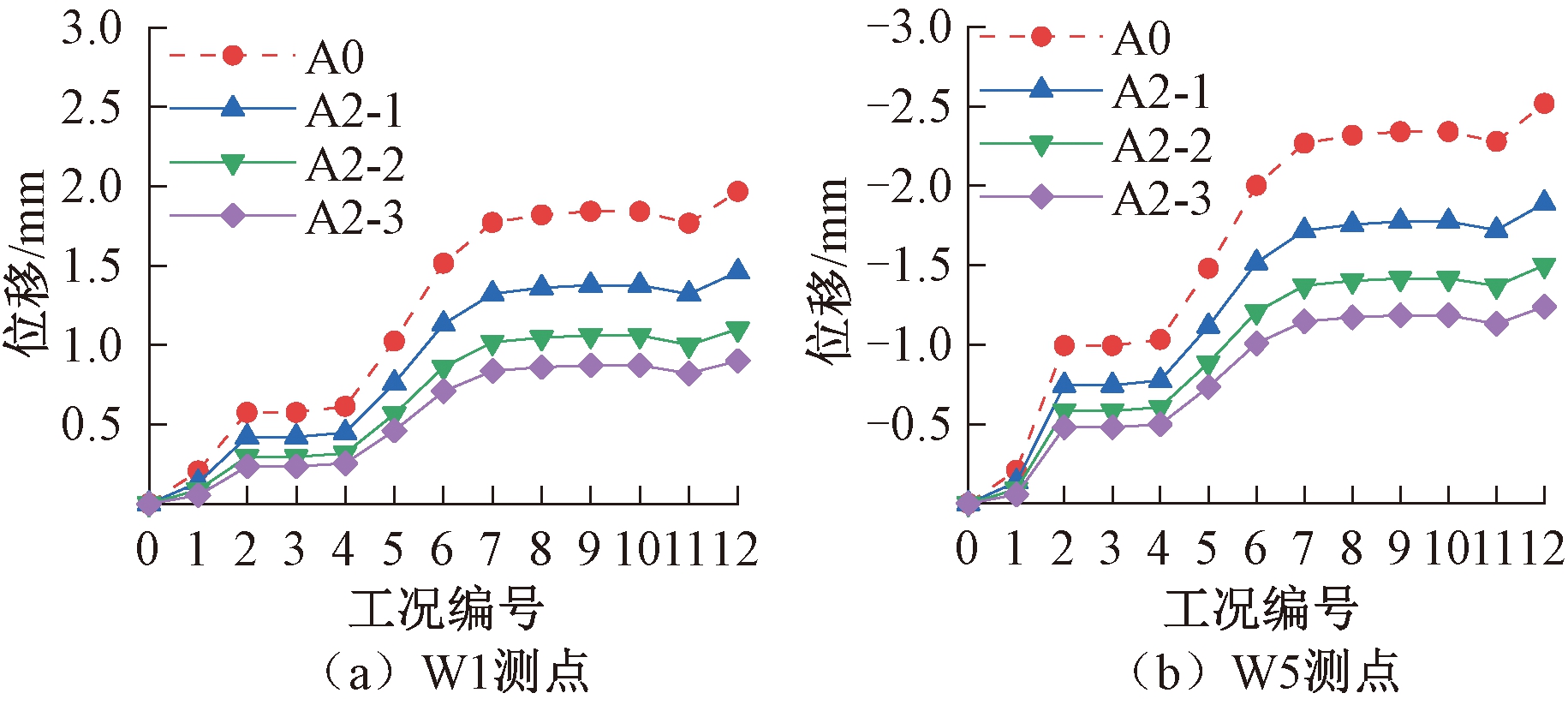
图8 方案A0和A2位移分析结果
Figure 8 Displacement analysis of scheme A0 and A2
由图8可知,设置基础系梁可使水平位移显著减小。随着系梁的数量增加,斜柱结构的基础水平位移相对方案A0分别减小约26.3%、42.4%、53.5%,可见增加系梁数量可以有效地控制基础水平位移,但控制效果会随系梁数量增加而减弱。
3.3 基础系梁截面刚度影响分析
杆件相对刚度会影响超静定结构的位移及内力,故方案A3分析了不同截面刚度下的结构内力和位移变化规律。截面刚度调整方法包括调整厚度(方案A3a)和直径(方案A3b),系梁截面构造见图9。考虑前节结果,系梁数量每侧2根。
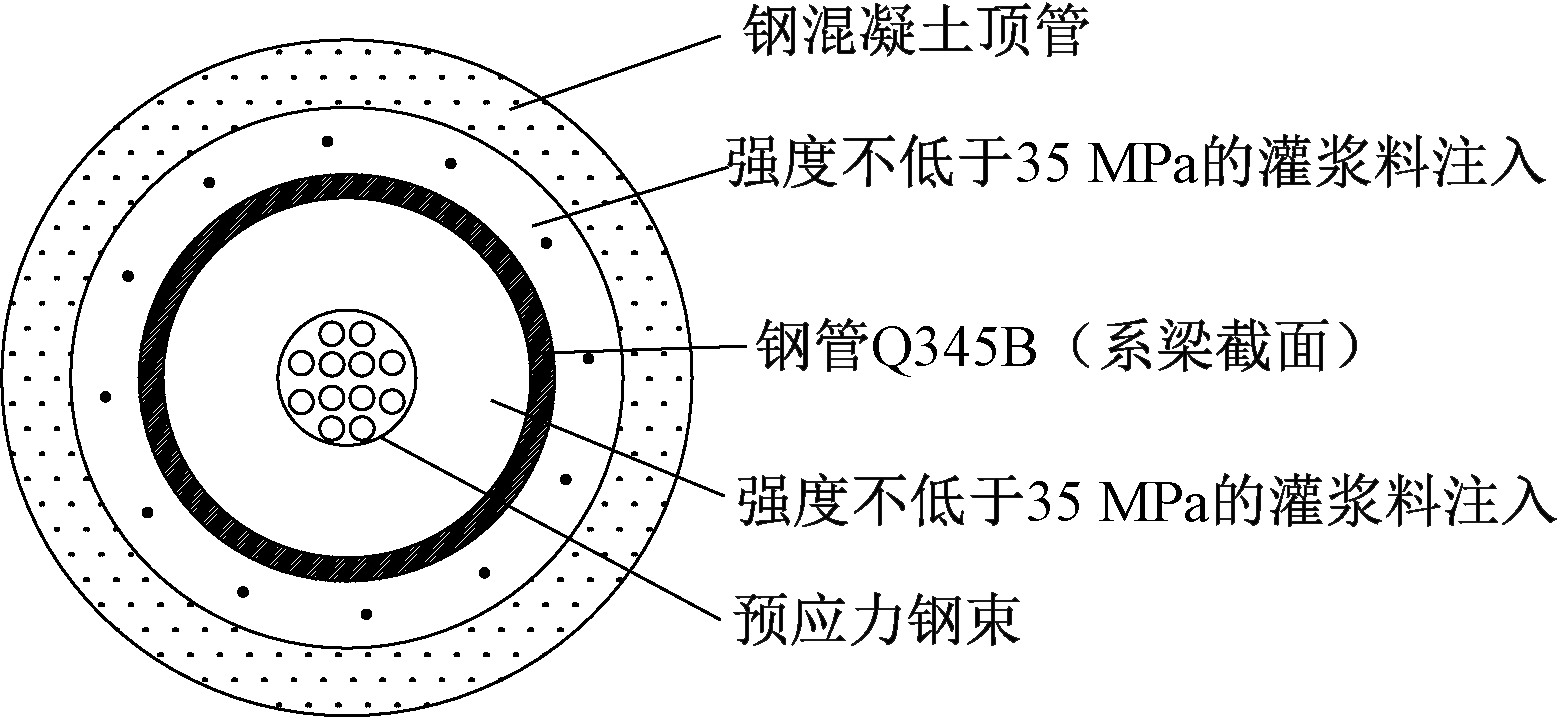
图9 预应力系梁横截面
Figure 9 Cross section of prestressed tie beam
3.3.1 系梁截面厚度影响分析
方案A3a研究基础系梁截面厚度变化对结构应力及位移的影响。各子方案的截面厚度分别为12、14、16、18、20 mm,相应的编号为A3a-1、A3a-2、A3a-3、A3a-4、A3a-5。图10、图11分别为柱脚、斜柱测点在各施工工况下的应力及位移变化情况。
由图10可知,系梁截面厚度变化对斜柱应力影响很小,不同子方案下结构应力差值均在3.0 MPa内。结合A2方案分析结果可知,设置系梁对上部结构应力影响很小,不会导致应力突变。
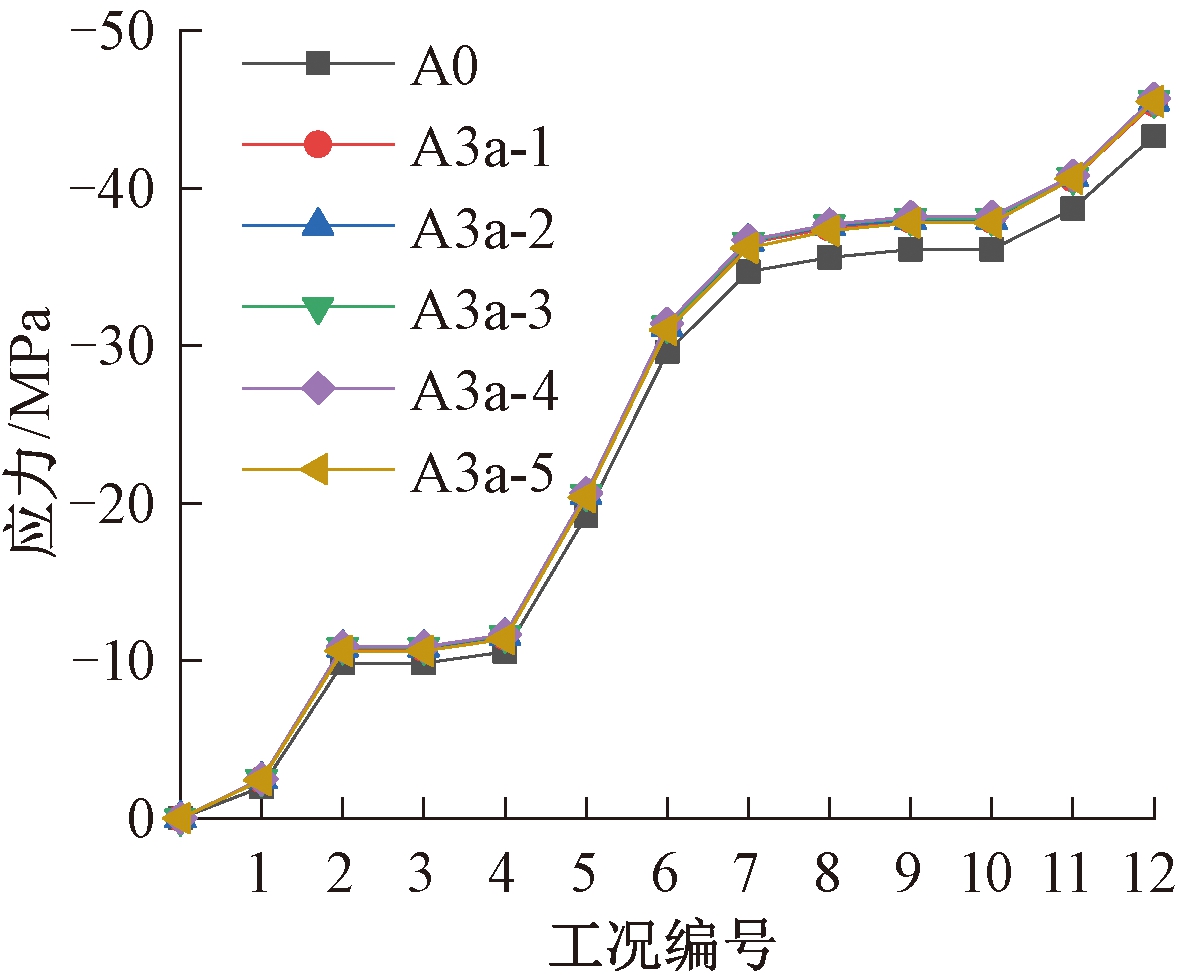
图10 方案A0和A3a斜柱应力分析结果
Figure 10 Stress analysis results of scheme A0 and A3a
由图11可知,各子方案位移最大绝对值分别为1.46、1.42、1.39、1.36、1.29 mm,采用基础系梁能有效控制基础水平位移,但截面厚度增加没有进一步减小基础位移,因此该方案对基础位移控制的优化效果可忽略。
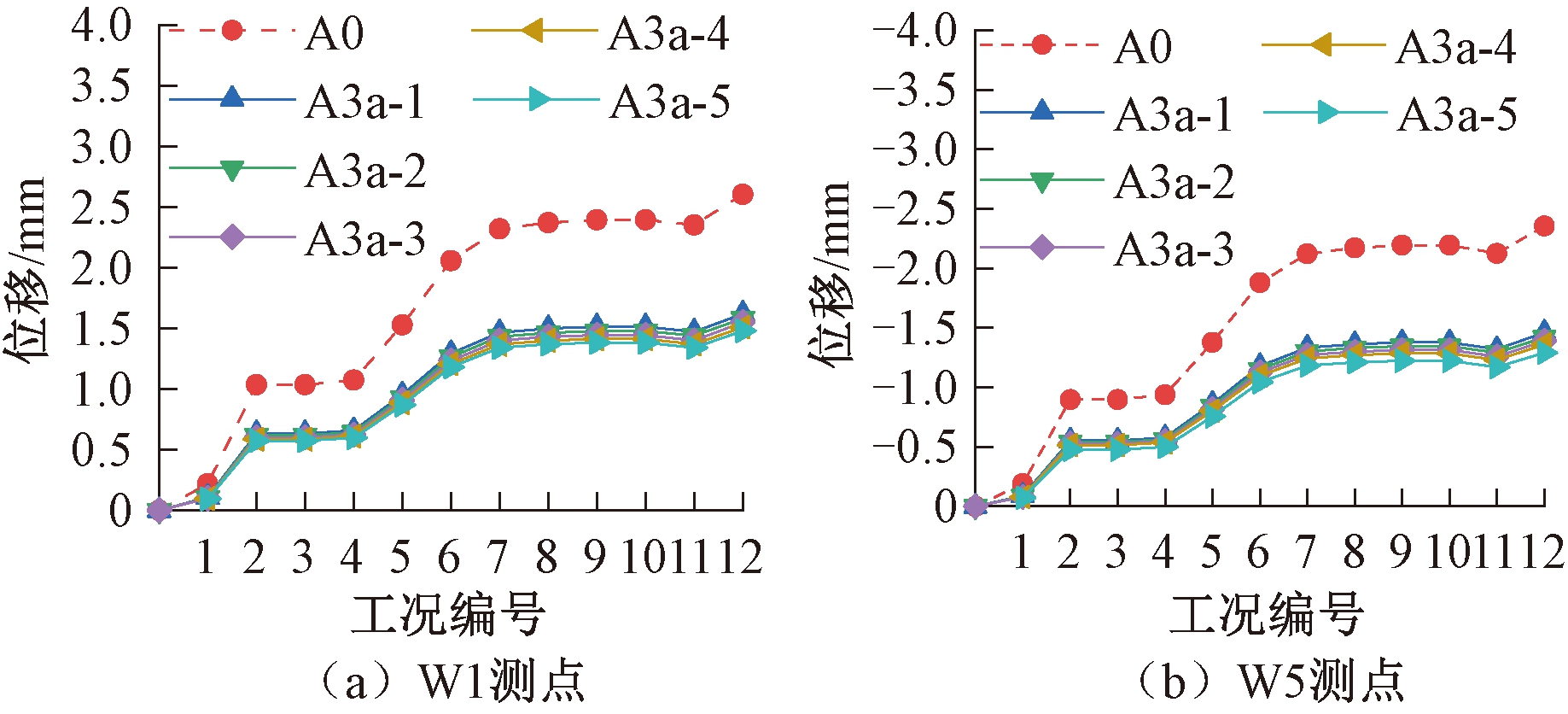
图11 方案A0和A3a位移分析结果
Figure 11 Displacement analysis of scheme A0 and A3a
3.3.2 系梁截面直径影响分析
由前节分析结果可知设置系梁对结构应力影响较小,因此方案A3b仅分析截面直径对位移的影响。参考前节结果,系梁截面厚度取14.0 mm。截面直径分别取0.2、0.4、0.6、0.8、1 m,对应编号为A3b-1、A3b-2、A3b-3、A3b-4、A3b-5。
各子方案下桩顶位移变化如图12所示。可以看出,采用基础系梁能有效减小基础位移,且增大系梁截面直径能进一步降低基础位移。各子方案下位移相对方案A0分别减小约40.3%、52.2%、61.2%、68.4%、74.3%。
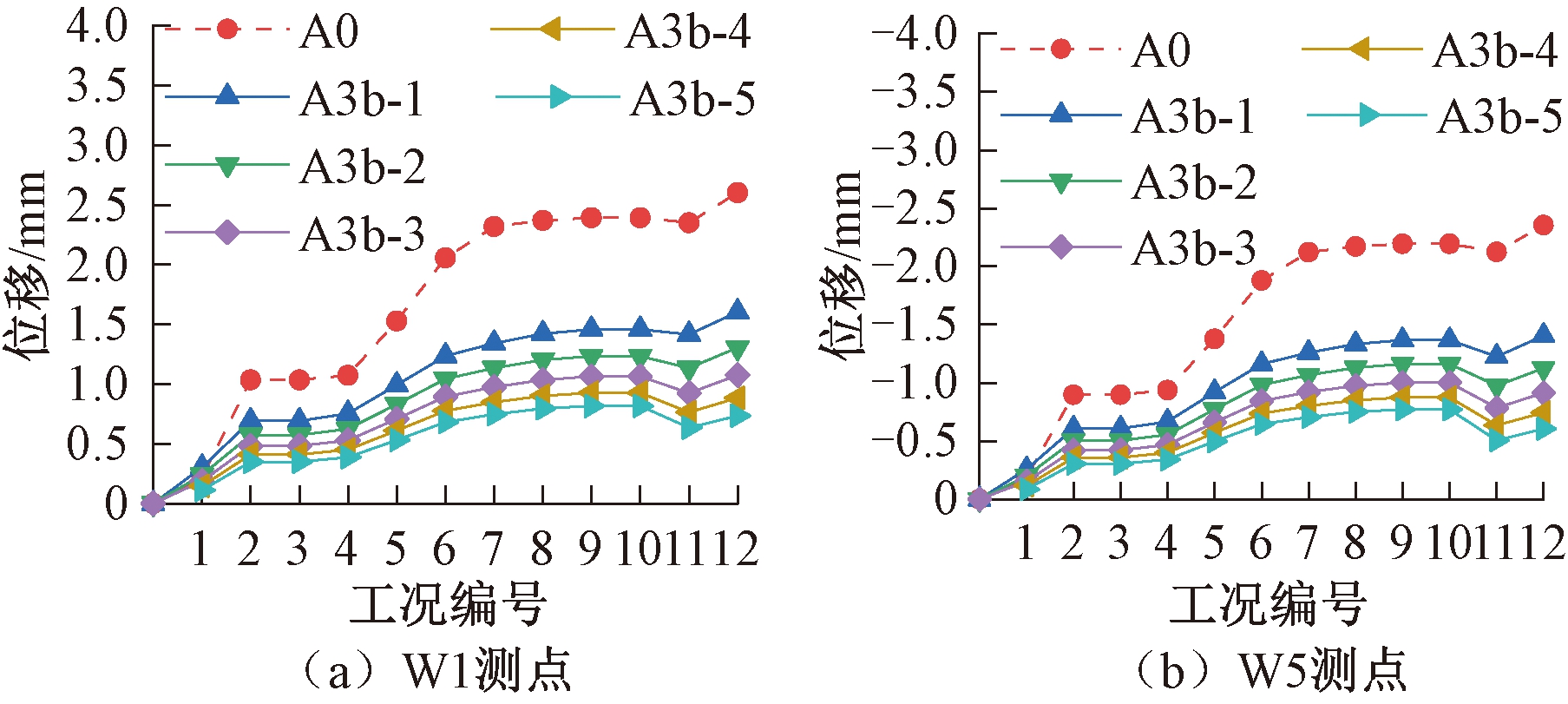
图12 方案A0和A3b位移分析结果
Figure 12 Displacement analysis of scheme A0 and A3b
4 结论
(1)由斜柱钢结构基础不同设计方案应力分析结果可知,基础系梁数量、刚度对上部结构应力影响较小,预应力方案有利于减小斜柱钢结构中斜柱的最大应力及桩顶水平位移,保证结构安全。
(2)由斜柱钢结构基础不同设计方案位移分析结果可知,采用系梁可有效降低基础位移;根据系梁数量不同,基础位移与未设置系梁相比可降低26%~53%;系梁截面厚度变化对位移影响较小;采用预应力系梁,各阶段基础位移普遍减小,预应力张拉后位移方向发生改变,且变形向多承台中心发展,更有利于位移控制及保障结构安全。
(3)根据基础位移控制设计指标及不同设计方案分析可知,基础系梁数量、截面直径以及预应力均可有效控制基础位移,其中采用预应力系梁设计方案时基础位移控制效果更优。
[1] 关吉平. 某博物馆大跨拱形入口结构设计[J]. 结构工程师, 2018, 34(5): 13-19.
GUAN J P. Design of large-span arch entrance structure of a museum[J]. Structural engineers, 2018, 34(5): 13-19.
[2] 杨伟, 宋汉东. 福州海峡国际会展中心扩建工程西区钢桁架施工过程监测[J]. 结构工程师, 2017, 33(4): 200-208.
YANG W, SONG H D. Construction monitoring of steel trusses for the expansion project of Fuzhou strait international conference exhibition western center[J]. Structural engineers, 2017, 33(4): 200-208.
[3] 刘学武. 大型复杂钢结构施工力学分析及应用研究[D]. 北京: 清华大学, 2008.
LIU X W. Analysis and application of construction mechanics of large complex steel structures[D]. Beijing: Tsinghua University, 2008.
[4] ZHANG W L, WU Z X, CHEN B H. Simulation study on construction process of complex spatial steel structure based on the construction mechanics[J]. Applied mechanics and materials, 2012, 226/227/228: 1209-1213.
[5] TIAN L M, HAO J P, WANG Y. The analysis of construction mechanical simulation of the large-span steel structure[C]//2009 International Conference on Information Management. Piscataway: IEEE, 2009: 150-153.
[6] ZHU B H, LI Z J, Chen G D, et al. The construction simulation of the large span steel roof of zayed national stadium [C]//Proceeding of Shanghai International Conference on Technology of Architecture and Structure. Shanghai: Tongji University Press, 2009:51-58.
[7] YAO G, WU C Y, YANG Y. Scientometric analysis for mechanical performance of broken-line long-span steel structure in construction considering geometric nonlinearity[J]. Symmetry, 2021, 13(7): 1229.
[8] 王昌兴, 徐珂, 田立强. 洛阳隋唐城天堂遗址保护建筑结构设计[J]. 钢结构, 2011, 26(8): 32-36, 79.
WANG C X, XU K, TIAN L Q. Structure design of Tiantang for the protection of the Ruins of ancient buildings built in the Sui and Tang dynasty in Luoyang City[J]. Steel construction, 2011, 26(8): 32-36, 79.
[9] 冯浩琪, 梁岩, 管品武, 等. 大跨钢结构基础预应力施工过程桩土作用影响分析[J]. 结构工程师, 2020, 36(3): 184-190.
FENG H Q, LIANG Y, GUAN P W, et al. Analysis of pile-soil interaction during prestressed construction of long-span steel structure foundation[J]. Structural engineers, 2020, 36(3): 184-190.
[10] 中华人民共和国建设部. 建筑桩基技术规范: JGJ 94—2008[S]. 北京: 中国建筑工业出版社, 2008.
Ministry of Construction of the People′s Republic of China. Technical code for building pile foundations: JGJ 94—2008[S]. Beijing: China Architecture & Building Press, 2008.
[11] 贺拴海, 贺小卫. 基于地基系数法的横向受荷桩通解研究[J]. 郑州大学学报(工学版), 2016, 37(3): 64-68.
HE S H, HE X W. The study of lateral load pile general solution based on modulus of subgrade reaction[J]. Journal of Zhengzhou university (engineering science), 2016, 37(3): 64-68.
[12] CHANG H, XIA J W. Constitutive model of disturbed soil-structure interface within mining subsidence areas[J]. Journal of central south university, 2017, 24(7): 1676-1683.